Fubini for continuous functions over intervals
|
|
|
- Evelyn Weaver
- 5 years ago
- Views:
Transcription
1 Fuini for ontinuous funtions over intervls We first prove the following theorem for ontinuous funtions. Theorem. Let f(x) e ontinuous on ompt intervl =[, [,. Then [, [, [ [ f(x, y)(x, y) = f(x, y)y x = f(x, y) x y. () Proof. As f(x, y) is ontinuous, for every fixe x n fixe y, f(x, y) n f(x, y ) re ontinuous. Furthermore, f(x, y)y n re lso ontinuous. Thus ll the ove integrls re well-efine. f(x, y)x (2) We prove [, [, [ f(x, y)(x, y)= f(x, y)y x (3) n the other equlity is similr. Wlog ssume = =, = =. Fix ny ε >. Sine f is ontinuous on [, [, it is uniformly ontinuous n there is δ > suh tht for ny x y <δ, f(x) f(y) < ε. (4) Now tke n N suh tht /n < δ/ 2 n ivie [, [, into squres of the form ij 8 [i h, (i+)h) [j h, (j + ) h) for i, j Z. Then we hve i, j, sup ij f inf ij f < ε. (5) Now efine g(x, y) 8 sup ij f, h(x, y) 8 inf ij f, (x, y) ij. (6) We hve g(x, y) f(x, y) h(x, y), g(x, y) h(x, y) <ε. (7) Now it n e heke through iret lultion tht g(x, y) = [ g(x, y) y x, h(x, y)= [ h(x, y)y x. (8)
2 Fix x=x. We hve g(x, y) f(x, y) h(x, y) (9) therefore g(x, y)y f(x, y)y h(x, y)y () for every x [,. Consequently This gives [ g(x, y)y x [ f(x, y)y x [ h(x, y)y x. () f(x, y) [ f(x, y)y x <ε (2) n the onlusion follows from the ritrriness of ε. Theorem 2. Let R N, J R M e ompt intervls n let f(x, y) e ontinuous on J. Then J [ [ f(x, y) (x, y)= f(x, y) y x= f(x, y) x y. (3) J J Proof. The proof is similr n is left s exerise. Corollry 3. Let f(x) e ontinuous on 8 [, [ N, N. Then we hve [ [ ( 2 ) N f(x)x = f(x,, x N )x N x 2 x (4) 2 N n the orer of the integrtion n e ritrrily hnge. Proof. Exerise. Exmple 4. Let A 8 [, [,. Clulte Solution. We write A A x e xy x y = xe xy xy. (5) = [ x [ x e xy y e z z x x 2
3 = (e x ) x = e 2. (6) Exerise. Let f C 2. Let = [, [,. Clulte 2 f xy. (7) x y Exerise 2. Clulte the followng. e x+y x y, = [, 2 ; (8) x 2 + y 2 x y, = [,2 ; (9) x sin(x y)xy, = [, π/2 [,. (2) sin(x + y) x y, = [, π/2 2 ; (2) y x 2 xy, = [, [,2; (22) Exerise 3. Let = [, 2. Clulte f(x, y)xy for the following f(x, y): y x 2 y > x 2 ; (23) x y x + y x + y > ; (24) x + y x 2 y 2 x 2. (25) elsewhere. Prolem. (USTC2) Construt B R 2 suh tht the following re stisfie.. for every R, B x = } n B y = } oth onsist of t most one single point. 2. B = R 2. Now efine Prove tht (x, y) B elsewhere. (26) ) Both exist n equl ; [ f(x, y)y x n [ f(x, y)x y (27) ) f is not integrle on [, 2. 3
4 Fuini: The generl se (Optionl) Two-vrile Fuini We still strt from the two-vrile se. Theorem 5. Let f(x, y): R 2 R e integrle on 8 [, [,. Further ssume tht for every x [,, f(x, y) s funtion of y is Riemnn integrle on [,. Then the funtion F(x) 8 is Riemnn integrle on [, n furthermore f(x, y) y (28) [ f(x, y)(x, y)= F(x) x= f(x, y)y x. (29) f furthermore for every y [,, f(x, y) s funtion of x is Riemnn integrle on [,, then we n swith the orer of integrtion: [ f(x, y)y [ x = f(x, y) x y = f(x, y) (x, y). (3) This theorem follows immeitely from the following result whih revels wht is relly going on here. Theorem 6. Let f(x, y): R 2 R n 8 [, [,. Define two funtions Φ(x) n φ(x) s follows: Φ(x) 8 U(f(x, ), [, ), φ(x) 8 L(f(x, ), [, ). (3) Here U(f(x,,[,)) n L(f(x, ),[,) enote the upper n lower integrls for the funtion f(x, y) trete s funtion of y lone (with x fixe). Then U(Φ(x), [, ) U(f(x, y), ); (32) L(φ(x), [, ) L(f(x, y), ). (33) Exerise 4. Prove Theorem 5 using Theorem 6. Remrk 7. From this theorem we see tht two imensionl Riemnn integrility puts strong restrition on the ehvior of the funtion long every slie. Exerise 5. Let f(x, y): R 2 R e integrle on 8 [, [,. For ny ε >, Let S ε 8 x [,P f(x, y) s funtion of y is not Riemnn integrle on [, n U(f,[,) L(f,[,)>ε}. Then µ (S ε )= where µ is the one-imensionl Jorn mesure. n other wors, if f(x, y) is integrle on, then most of its slies re Riemnn integrle. Remrk 8. Note tht in the ove exerise we nnot reple S ε y S 8 x [, P f(x, y) s funtion of y is not Riemnn integrle on [, }. See the prolem elow. 4
5 Prolem 2. Let x Q, y Q p x= r, (p, r) o-prime; y Q p f(x, y) 8 q x Q, y = s. (34), (s, q) o-prime q x Q, y Q Prove tht f(x, y) is Riemnn integrle on [, [,. But for every x [, Q, f(x, y) is not Riemnn integrle on [,. Proof. (of Theorem 6) Rell our results regring uniform prtition. For ny n N, set h 8 n n h 2 8. Let n ij,h 8 [ +(i )h, + ih [ + (j )h 2, + jh 2. Then we know tht lim f ij h h 2 = lim F ij h h 2 = f(x, y)(x, y) (35) n n i,j= i,j= where f ij 8 Now for eh (i, j), we hve inf f(x, y), F ij 8 sup f(x, y). (36) (x,y) ij,h (x,y) ij,h (x, y) ij,h, f ij f(x, y) f ij h 2 L(f(x, y), [ +(j )h 2, + jh 2 ); (37) Sine this is true for ll x [ + (i )h, +ih, we hve f ij h h 2 L(L(f(x, y), [ + (j )h 2, + jh 2 ), [ + (i )h, + ih ). (38) Now summing over i, j we hve f ij h h 2 L(φ(x), [, ). (39) i,j= The other inequlity n e prove similrly. Exerise 6. Let f: R R, < <. Prove tht Generl ses The proof for the generl se is similr. L(f, [, )+L(f,[, ) = L(f, [, ). (4) Theorem 9. (Fuini) Let f(x, y) (x R M, y R N ) e integrle on 8 2 where R M, 2 R N. Assume tht for every x the funtion f(x, y) s funtion of y only is integrle on 2, then [ f(x, y)(x, y)= f(x, y)y x. (4) 2 f furthermore for every y 2 the funtion f(x, y) s funtion of x only is integrle on, then [ 2 f(x, y)y [ x = f(x, y)x y = f(x, y)(x, y). (42) 2 Exerise 7. Let A:=(x, y, z)p x 2 + y 2 + z 2 }. Prove tht [ µ(a) = z 2 z 2 ( z 2 y 2 z 2 y 2 x ) y z. (43) 5
Double Integrals over Rectangles
 Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of
Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of
Lecture 16. Double integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Functions of several variables
 Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Vector Calculus. 1 Line Integrals
 Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
(1) Primary Trigonometric Ratios (SOH CAH TOA): Given a right triangle OPQ with acute angle, we have the following trig ratios: ADJ
 Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
13.1 Double Integral over Rectangle. f(x ij,y ij ) i j I <ɛ. f(x, y)da.
 CHAPTE 3, MULTIPLE INTEGALS Definition. 3. Double Integrl over ectngle A function f(x, y) is integrble on rectngle [, b] [c, d] if there is number I such tht for ny given ɛ>0thereisδ>0 such tht, fir ny
CHAPTE 3, MULTIPLE INTEGALS Definition. 3. Double Integrl over ectngle A function f(x, y) is integrble on rectngle [, b] [c, d] if there is number I such tht for ny given ɛ>0thereisδ>0 such tht, fir ny
Notes on Spherical Triangles
 Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
Example. Check that the Jacobian of the transformation to spherical coordinates is
 lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
10.4 AREAS AND LENGTHS IN POLAR COORDINATES
 65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
MATH 118 PROBLEM SET 6
 MATH 118 PROBLEM SET 6 WASEEM LUTFI, GABRIEL MATSON, AND AMY PIRCHER Section 1 #16: Show tht if is qudrtic residue modulo m, nd b 1 (mod m, then b is lso qudrtic residue Then rove tht the roduct of the
MATH 118 PROBLEM SET 6 WASEEM LUTFI, GABRIEL MATSON, AND AMY PIRCHER Section 1 #16: Show tht if is qudrtic residue modulo m, nd b 1 (mod m, then b is lso qudrtic residue Then rove tht the roduct of the
Multivariable integration. Multivariable integration. Iterated integration
 Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Chapter 12 Vectors and the Geometry of Space 12.1 Three-dimensional Coordinate systems
 hpter 12 Vectors nd the Geometry of Spce 12.1 Three-dimensionl oordinte systems A. Three dimensionl Rectngulr oordinte Sydstem: The rtesin product where (x, y, z) isclled ordered triple. B. istnce: R 3
hpter 12 Vectors nd the Geometry of Spce 12.1 Three-dimensionl oordinte systems A. Three dimensionl Rectngulr oordinte Sydstem: The rtesin product where (x, y, z) isclled ordered triple. B. istnce: R 3
Polar Coordinates. July 30, 2014
 Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Section 17.2: Line Integrals. 1 Objectives. 2 Assignments. 3 Maple Commands. 1. Compute line integrals in IR 2 and IR Read Section 17.
 Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Math 116 Calculus II
 Mth 6 Clculus II Contents 7 Additionl topics in Integrtion 7. Integrtion by prts..................................... 7.4 Numericl Integrtion.................................... 7 7.5 Improper Integrl......................................
Mth 6 Clculus II Contents 7 Additionl topics in Integrtion 7. Integrtion by prts..................................... 7.4 Numericl Integrtion.................................... 7 7.5 Improper Integrl......................................
Domination and Independence on Square Chessboard
 Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world
 Person Edution Limited Edinurgh Gte Hrlow Essex M20 2JE Englnd nd ssoited ompnies throughout the world Visit us on the World Wide We t: www.personed.o.uk Person Edution Limited 2014 ll rights reserved.
Person Edution Limited Edinurgh Gte Hrlow Essex M20 2JE Englnd nd ssoited ompnies throughout the world Visit us on the World Wide We t: www.personed.o.uk Person Edution Limited 2014 ll rights reserved.
NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES
 At Mth Univ Comenine Vol LXXXV, (06, pp 07 07 NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES G FARID Abstrt In this pper, new Ostrowski-type inequlities in two oordintes re estblished
At Mth Univ Comenine Vol LXXXV, (06, pp 07 07 NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES G FARID Abstrt In this pper, new Ostrowski-type inequlities in two oordintes re estblished
ITEC2620 Introduction to Data Structures
 /5/20 ITEC220 Introdution to Dt Strutures Leture 0 Gme Trees Two-Plyer Gmes Rules for gme define the sttespe Nodes re gme sttes Links re possile moves Build serh tree y rute fore Exmple I Exmple II A Our
/5/20 ITEC220 Introdution to Dt Strutures Leture 0 Gme Trees Two-Plyer Gmes Rules for gme define the sttespe Nodes re gme sttes Links re possile moves Build serh tree y rute fore Exmple I Exmple II A Our
Lecture 20. Intro to line integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Section 16.3 Double Integrals over General Regions
 Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
Math 232. Calculus III Limits and Continuity. Updated: January 13, 2016 Calculus III Section 14.2
 Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
ASY P.O. BOX 729 TERRELL, TEXAS / PAGE 1 OF 13 SAM
 203 Madix Inc., ll rights reserved ommon Parts 2 MXI GRI WIRE GRI SHELF WITH (GPWGS) MXI GRI FIXTURE PNEL (GPWFP) FIXTURE PNELS RE USE S EN SUPPORT. SHELF N E USE NYWHERE. MXI GRI REINFORMENT R 3 (GPR)
203 Madix Inc., ll rights reserved ommon Parts 2 MXI GRI WIRE GRI SHELF WITH (GPWGS) MXI GRI FIXTURE PNEL (GPWFP) FIXTURE PNELS RE USE S EN SUPPORT. SHELF N E USE NYWHERE. MXI GRI REINFORMENT R 3 (GPR)
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Geometric quantities for polar curves
 Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations
 54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
Computational Complexity of a Pop-up Book
 omputtionl omplexity of Pop-up ook Ryuhei Uehr Shio Termoto strt Origmi is the enturies-ol rt of foling pper, n reently, it is investigte s omputer siene: Given n origmi ith reses, the prolem to etermine
omputtionl omplexity of Pop-up ook Ryuhei Uehr Shio Termoto strt Origmi is the enturies-ol rt of foling pper, n reently, it is investigte s omputer siene: Given n origmi ith reses, the prolem to etermine
Defining the Rational Numbers
 MATH10 College Mthemtis - Slide Set 2 1. Rtionl Numers 1. Define the rtionl numers. 2. Redue rtionl numers.. Convert etween mixed numers nd improper frtions. 4. Express rtionl numers s deimls.. Express
MATH10 College Mthemtis - Slide Set 2 1. Rtionl Numers 1. Define the rtionl numers. 2. Redue rtionl numers.. Convert etween mixed numers nd improper frtions. 4. Express rtionl numers s deimls.. Express
Patterns and Algebra
 Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Section 15.3 Partial Derivatives
 Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Resistors, Current and Voltage measurements, Ohm s law, Kirchhoff s first and second law. Kirchhoff s first Objectives:
 EE -050 Ciruit L Experiment # esistors, Current nd Voltge mesurements, Ohm s lw, Kirhhoff s first nd seond lw. Kirhhoff s first Ojetives: Slmn in Adul Aziz University Eletril Engineering Deprtment. Fmiliriztion
EE -050 Ciruit L Experiment # esistors, Current nd Voltge mesurements, Ohm s lw, Kirhhoff s first nd seond lw. Kirhhoff s first Ojetives: Slmn in Adul Aziz University Eletril Engineering Deprtment. Fmiliriztion
Macroscopic and Microscopic Springs Procedure
 Mrosopi nd Mirosopi Springs Proedure OBJECTIVE Purpose In this l you will: investigte the spring-like properties of stright wire, disover the strethiness of mteril, independent of the size nd shpe of n
Mrosopi nd Mirosopi Springs Proedure OBJECTIVE Purpose In this l you will: investigte the spring-like properties of stright wire, disover the strethiness of mteril, independent of the size nd shpe of n
Regular languages can be expressed as regular expressions.
 Regulr lnguges cn e expressed s regulr expressions. A generl nondeterministic finite utomton (GNFA) is kind of NFA such tht: There is unique strt stte nd is unique ccept stte. Every pir of nodes re connected
Regulr lnguges cn e expressed s regulr expressions. A generl nondeterministic finite utomton (GNFA) is kind of NFA such tht: There is unique strt stte nd is unique ccept stte. Every pir of nodes re connected
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES
 MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables
 Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Differentiable functions (Sec. 14.4)
 Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 2411 Calc III Practice Exam 2
 Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
THIS LECTURE looks at bell ringing (the posh name is Tintinnalogia) which as. WE NORMALLY think of a bell as hanging mouth down. If we swing the bell,
 7 Bells THIS LECTURE looks t ell ringing (the posh nme is Tintinnlogi) whih s n orgnize tivity hs een roun for long time. Inee, n importnt ook y Stemn on the sujet ws pulishe in 1668 (two yers fter the
7 Bells THIS LECTURE looks t ell ringing (the posh nme is Tintinnlogi) whih s n orgnize tivity hs een roun for long time. Inee, n importnt ook y Stemn on the sujet ws pulishe in 1668 (two yers fter the
Solutions to the problems from Written assignment 2 Math 222 Winter 2015
 Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
Math 32, October 22 & 27: Maxima & Minima
 Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
REVIEW QUESTIONS TOPIC 5 TRIGONOMETRY I FLUENCY
 TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
Probability and Statistics P(A) Mathletics Instant Workbooks. Copyright
 Proility nd Sttistis Student Book - Series K- P(A) Mthletis Instnt Workooks Copyright Student Book - Series K Contents Topis Topi - Review of simple proility Topi - Tree digrms Topi - Proility trees Topi
Proility nd Sttistis Student Book - Series K- P(A) Mthletis Instnt Workooks Copyright Student Book - Series K Contents Topis Topi - Review of simple proility Topi - Tree digrms Topi - Proility trees Topi
Balancing Your Life. Ideas that might help you
 Blning Your Life Ides tht might help you Pul Hoskin Summer 2007 Let s e honest if one lists off the responsiilities nd hoies tht eh of us hve nd ssigns weekly hourly time tht eh needs to e fulfilled, then
Blning Your Life Ides tht might help you Pul Hoskin Summer 2007 Let s e honest if one lists off the responsiilities nd hoies tht eh of us hve nd ssigns weekly hourly time tht eh needs to e fulfilled, then
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
MATH 105: Midterm #1 Practice Problems
 Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
& Y Connected resistors, Light emitting diode.
 & Y Connected resistors, Light emitting diode. Experiment # 02 Ojectives: To get some hndson experience with the physicl instruments. To investigte the equivlent resistors, nd Y connected resistors, nd
& Y Connected resistors, Light emitting diode. Experiment # 02 Ojectives: To get some hndson experience with the physicl instruments. To investigte the equivlent resistors, nd Y connected resistors, nd
MULTI-VARIABLE OPTIMIZATION NOTES. 1. Identifying Critical Points
 MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
Green puzzles are the easiest and focus on two foundational skills: subtracting single-digit numbers and making sums of 10.
 Puzzle Instrutions! Use ONLY wet-erse mrkers. Any other mrker my permnently dmge the sheets. Smrt Sutrt Puzzles omine the fun nd ingenuity of puzzles with the repetition nd prtie kids need to mster their
Puzzle Instrutions! Use ONLY wet-erse mrkers. Any other mrker my permnently dmge the sheets. Smrt Sutrt Puzzles omine the fun nd ingenuity of puzzles with the repetition nd prtie kids need to mster their
Kirchhoff s Rules. Kirchhoff s Laws. Kirchhoff s Rules. Kirchhoff s Laws. Practice. Understanding SPH4UW. Kirchhoff s Voltage Rule (KVR):
 SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
b = and their properties: b 1 b 2 b 3 a b is perpendicular to both a and 1 b = x = x 0 + at y = y 0 + bt z = z 0 + ct ; y = y 0 )
 ***************** Disclimer ***************** This represents very brief outline of most of the topics covered MA261 *************************************************** I. Vectors, Lines nd Plnes 1. Vector
***************** Disclimer ***************** This represents very brief outline of most of the topics covered MA261 *************************************************** I. Vectors, Lines nd Plnes 1. Vector
ECE 274 Digital Logic Spring Digital Design. Combinational Logic Design Process and Common Combinational Components Digital Design
 ECE 27 Digitl Logi Spring 29 Comintionl Logi Design Proess n Common Comintionl Components Digitl Design 2.7 2. Digitl Design Chpter 2: Comintionl Logi Design Slies to ompn the tetook Digitl Design, irst
ECE 27 Digitl Logi Spring 29 Comintionl Logi Design Proess n Common Comintionl Components Digitl Design 2.7 2. Digitl Design Chpter 2: Comintionl Logi Design Slies to ompn the tetook Digitl Design, irst
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
NUMBER THEORY Amin Witno
 WON Series in Discrete Mthemtics nd Modern Algebr Volume 2 NUMBER THEORY Amin Witno Prefce Written t Phildelphi University, Jordn for Mth 313, these notes 1 were used first time in the Fll 2005 semester.
WON Series in Discrete Mthemtics nd Modern Algebr Volume 2 NUMBER THEORY Amin Witno Prefce Written t Phildelphi University, Jordn for Mth 313, these notes 1 were used first time in the Fll 2005 semester.
Chapter 16. Partial Derivatives
 Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Review #Final Exam MATH 142-Drost
 Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
B) 0 C) 1 D) No limit. x2 + y2 4) A) 2 B) 0 C) 1 D) No limit. A) 1 B) 2 C) 0 D) No limit. 8xy 6) A) 1 B) 0 C) π D) -1
 MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
Math Lecture 2 Inverse Functions & Logarithms
 Math 1060 Lecture 2 Inverse Functions & Logarithms Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms
Math 1060 Lecture 2 Inverse Functions & Logarithms Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms
Copyright 2009 Pearson Education, Inc. Slide Section 8.2 and 8.3-1
 8.3-1 Transformation of sine and cosine functions Sections 8.2 and 8.3 Revisit: Page 142; chapter 4 Section 8.2 and 8.3 Graphs of Transformed Sine and Cosine Functions Graph transformations of y = sin
8.3-1 Transformation of sine and cosine functions Sections 8.2 and 8.3 Revisit: Page 142; chapter 4 Section 8.2 and 8.3 Graphs of Transformed Sine and Cosine Functions Graph transformations of y = sin
Test Yourself. 11. The angle in degrees between u and w. 12. A vector parallel to v, but of length 2.
 Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Practice Test (page 201) 1. A. This is not true because 64 has these factors: 1, 2, 4, 8, 16, 32, and 64 So, A is the correct answer.
 Practice Test (page 201) 1. A. This is not true because 64 has these factors: 1, 2, 4, 8, 16, 32, and 64 So, A is the correct answer. 2. Expand each product until the trinomial matches the given trinomial.
Practice Test (page 201) 1. A. This is not true because 64 has these factors: 1, 2, 4, 8, 16, 32, and 64 So, A is the correct answer. 2. Expand each product until the trinomial matches the given trinomial.
Spherical Geometry. This is an article from my home page:
 Spheril Geometry This is n rtile from my home pge: www.olewitthnsen.dk Ole Witt-Hnsen nov. 6 Contents. Geometry on sphere.... Spheril tringles...3. Polr tringles...4 3. The right-ngle spheril tringle...6
Spheril Geometry This is n rtile from my home pge: www.olewitthnsen.dk Ole Witt-Hnsen nov. 6 Contents. Geometry on sphere.... Spheril tringles...3. Polr tringles...4 3. The right-ngle spheril tringle...6
Solutions to exercise 1 in ETS052 Computer Communication
 Solutions to exercise in TS52 Computer Communiction 23 Septemer, 23 If it occupies millisecond = 3 seconds, then second is occupied y 3 = 3 its = kps. kps If it occupies 2 microseconds = 2 6 seconds, then
Solutions to exercise in TS52 Computer Communiction 23 Septemer, 23 If it occupies millisecond = 3 seconds, then second is occupied y 3 = 3 its = kps. kps If it occupies 2 microseconds = 2 6 seconds, then
SOLVING TRIANGLES USING THE SINE AND COSINE RULES
 Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Math Circles Finite Automata Question Sheet 3 (Solutions)
 Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Proposed Cable Tables for SAS2
 Tle 50 Requirements for internl le ssemlies using SASDrive onnetors n kplnes. Requirement, Units 1,5 Gps 3Gps 6 Gps Bulk le or kplne:, Differentil impene ohm 100 ± 10 100 g Common-moe impene ohm 32,5 ±
Tle 50 Requirements for internl le ssemlies using SASDrive onnetors n kplnes. Requirement, Units 1,5 Gps 3Gps 6 Gps Bulk le or kplne:, Differentil impene ohm 100 ± 10 100 g Common-moe impene ohm 32,5 ±
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY
 LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
WI1402-LR Calculus II Delft University of Technology
 WI402-LR lculus II elft University of Technology Yer 203 204 Michele Fcchinelli Version.0 Lst modified on Februry, 207 Prefce This summry ws written for the course WI402-LR lculus II, tught t the elft
WI402-LR lculus II elft University of Technology Yer 203 204 Michele Fcchinelli Version.0 Lst modified on Februry, 207 Prefce This summry ws written for the course WI402-LR lculus II, tught t the elft
14.7 Maximum and Minimum Values
 CHAPTER 14. PARTIAL DERIVATIVES 115 14.7 Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at
CHAPTER 14. PARTIAL DERIVATIVES 115 14.7 Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at
NONCLASSICAL CONSTRUCTIONS II
 NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
CS 135: Computer Architecture I. Boolean Algebra. Basic Logic Gates
 Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Microwave Magnetics. Graduate Course Electrical Engineering (Communications) 2 nd Semester, Sharif University of Technology
 Microwave Magnetics Graduate Course Electrical Engineering (Communications) 2 nd Semester, 389-39 Sharif University of Technology General information Contents of lecture 8: Waveguide resonators General
Microwave Magnetics Graduate Course Electrical Engineering (Communications) 2 nd Semester, 389-39 Sharif University of Technology General information Contents of lecture 8: Waveguide resonators General
Student Book SERIES. Patterns and Algebra. Name
 E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
Unilateral and equitransitive tilings by squares of four sizes
 Also ville t http://m-journl.eu ISSN 1855-3966 (printe en.), ISSN 1855-3974 (eletroni en.) ARS MATHEMATICA CONTEMPORANEA 10 (2015) 135 167 Unilterl n equitrnsitive tilings y squres of four sizes Csey Mnn
Also ville t http://m-journl.eu ISSN 1855-3966 (printe en.), ISSN 1855-3974 (eletroni en.) ARS MATHEMATICA CONTEMPORANEA 10 (2015) 135 167 Unilterl n equitrnsitive tilings y squres of four sizes Csey Mnn
Lecture 19. Vector fields. Dan Nichols MATH 233, Spring 2018 University of Massachusetts. April 10, 2018.
 Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Changing the routing protocol without transient loops
 Chnging the routing protool without trnsient loops Nny Rhkiy, Alexnre Guitton To ite this version: Nny Rhkiy, Alexnre Guitton. Chnging the routing protool without trnsient loops. Computer Communitions,
Chnging the routing protool without trnsient loops Nny Rhkiy, Alexnre Guitton To ite this version: Nny Rhkiy, Alexnre Guitton. Chnging the routing protool without trnsient loops. Computer Communitions,
y = sin x 5.5 Graphing sine and cosine functions
 Graphing sine and csine functins: Class ntes, G. Battaly 5.5 Graphing sine and csine functins GOALS: 1. Recgnize that f(x) = sin x and g(x) = cs x are functins. (Each value f x results in exactly 1 y value.)
Graphing sine and csine functins: Class ntes, G. Battaly 5.5 Graphing sine and csine functins GOALS: 1. Recgnize that f(x) = sin x and g(x) = cs x are functins. (Each value f x results in exactly 1 y value.)
3878 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 61, NO. 9, SEPTEMBER Optimal Algorithms for Near-Hitless Network Restoration via Diversity Coding
 3878 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 6, NO. 9, SEPTEMBER 23 Optiml Algorithms for Ner-Hitless Network Restortion vi Diversity Coing Serht Nzim Avi, Stuent Memer, IEEE, n Ener Aynoglu, Fellow,
3878 IEEE TRANSACTIONS ON COMMUNICATIONS, VOL. 6, NO. 9, SEPTEMBER 23 Optiml Algorithms for Ner-Hitless Network Restortion vi Diversity Coing Serht Nzim Avi, Stuent Memer, IEEE, n Ener Aynoglu, Fellow,
Independent of path Green s Theorem Surface Integrals. MATH203 Calculus. Dr. Bandar Al-Mohsin. School of Mathematics, KSU 20/4/14
 School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
Patterns and Relationships
 Series Techer Ptterns nd Reltionships opyright 009 3P Lerning. All rights reserved. First edition printed 009 in Austrli. A ctlogue record for this ook is ville from 3P Lerning Ltd. ISBN 978-1-91860-3-4
Series Techer Ptterns nd Reltionships opyright 009 3P Lerning. All rights reserved. First edition printed 009 in Austrli. A ctlogue record for this ook is ville from 3P Lerning Ltd. ISBN 978-1-91860-3-4
AGA56... Analog Input Modules. Siemens Building Technologies HVAC Products
 7 922 nlog Input odules G56... nlog input modules for the ontrol of SQ5... ir dmper tutors y ontinuous nlog ontrol signls, suh s 4...20 m, nd ontinuous nlog position feedk signls. For supplementry Dt Sheets,
7 922 nlog Input odules G56... nlog input modules for the ontrol of SQ5... ir dmper tutors y ontinuous nlog ontrol signls, suh s 4...20 m, nd ontinuous nlog position feedk signls. For supplementry Dt Sheets,
Samantha s Strategies page 1 of 2
 Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
14.2 Limits and Continuity
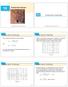 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
Section 6.1 Law of Sines. Notes. Oblique Triangles - triangles that have no right angles. A c. A is acute. A is obtuse
 Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Review guide for midterm 2 in Math 233 March 30, 2009
 Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Exercise 1-1. The Sine Wave EXERCISE OBJECTIVE DISCUSSION OUTLINE. Relationship between a rotating phasor and a sine wave DISCUSSION
 Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Maxima and Minima. Terminology note: Do not confuse the maximum f(a, b) (a number) with the point (a, b) where the maximum occurs.
 10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
Aluminium Roof Outlets - Introduction to Detail Outlets
 Aluminium Roof Outlets - Introution to Detil Outlets The Hrmer Roof Detil rnge inlues outlets to over ll the wkwr etiling situtions tht our in uiling esign n in refurishment. Min Chrteristis Hrmer Roof
Aluminium Roof Outlets - Introution to Detil Outlets The Hrmer Roof Detil rnge inlues outlets to over ll the wkwr etiling situtions tht our in uiling esign n in refurishment. Min Chrteristis Hrmer Roof
Determine currents I 1 to I 3 in the circuit of Fig. P2.14. Solution: For the loop containing the 18-V source, I 1 = 0.
 Prolem.14 Determine currents 1 to 3 in the circuit of Fig. P.14. 1 A 18 V Ω 3 A 1 8 Ω 1 Ω 7 Ω 4 Ω 3 Figure P.14: Circuit for Prolem.14. For the loop contining the 18-V source, Hence, 1 = 1.5 A. KCL t node
Prolem.14 Determine currents 1 to 3 in the circuit of Fig. P.14. 1 A 18 V Ω 3 A 1 8 Ω 1 Ω 7 Ω 4 Ω 3 Figure P.14: Circuit for Prolem.14. For the loop contining the 18-V source, Hence, 1 = 1.5 A. KCL t node
Triangles and parallelograms of equal area in an ellipse
 1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Student Book SERIES. Fractions. Name
 D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
MATH 261 EXAM II PRACTICE PROBLEMS
 MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
Partial Differentiation 1 Introduction
 Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
EQ: What are the similarities and differences between matrices and real numbers?
 Unit 4 Lesson 1 Essentil Question Stndrds Objectives Vocbulry Mtrices Mtrix Opertions Wht re the similrities nd differences between mtrices nd rel numbers? M.ALGII.2.4 Unit 4: Lesson 1 Describe how you
Unit 4 Lesson 1 Essentil Question Stndrds Objectives Vocbulry Mtrices Mtrix Opertions Wht re the similrities nd differences between mtrices nd rel numbers? M.ALGII.2.4 Unit 4: Lesson 1 Describe how you
Understanding Three-Phase Transformers
 PDH ourse E450 (4 PDH) Understnding Three-Phse Trnsformers Rlph Fehr, Ph.D., P.E. 2014 PDH Online PDH enter 5272 Medow Esttes Drive Firfx, V 22030-6658 Phone & Fx: 703-988-0088 www.pdhonline.org www.pdhenter.om
PDH ourse E450 (4 PDH) Understnding Three-Phse Trnsformers Rlph Fehr, Ph.D., P.E. 2014 PDH Online PDH enter 5272 Medow Esttes Drive Firfx, V 22030-6658 Phone & Fx: 703-988-0088 www.pdhonline.org www.pdhenter.om
Elettra Evolution OK! OK! b. User manual
 Elettr Evolution User mnul Pg. 1 INSTALLING THE SOLENOID VALVE. The progrmmle solenoi vlve is fully wtertight n will funtion even if instlle permnently uner wter t epth of up to one metre (IP68 ingress
Elettr Evolution User mnul Pg. 1 INSTALLING THE SOLENOID VALVE. The progrmmle solenoi vlve is fully wtertight n will funtion even if instlle permnently uner wter t epth of up to one metre (IP68 ingress
ECE380 Digital Logic
 ECE38 Digital Logic Introduction Dr. D. J. Jackson Lecture - Digital hardware Logic circuits are used to build computer hardware as well as other products (digital hardware) Late 96 s and early 97 s saw
ECE38 Digital Logic Introduction Dr. D. J. Jackson Lecture - Digital hardware Logic circuits are used to build computer hardware as well as other products (digital hardware) Late 96 s and early 97 s saw
