Double Integrals over Rectangles
|
|
|
- Daniel Crawford
- 5 years ago
- Views:
Transcription
1 Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of funtion f(x) over n intervl [, b ws defined to be b f(x) dx lim f(x i )Δx, where Δx (b )/n, nd, for eh i, x i x i x i, where x i + iδx. The purpose of the definite integrl is to ompute the re of region with urved boundry, using the formul for the re of retngle. The summtion used to define the integrl is the sum of the res of n retngles, eh with width Δx, nd height f(x i ), for i,,..., n. By tking the limit s n, the number of retngles, tends to infinity, we obtin the sum of the res of infinitely mny retngles of infinitely smll width. We define the re of the region bounded by the lines x, y, x b, nd the urve y f(x), to be this limit, if it exists. Unfortuntely, it is too tedious to ompute definite integrls using this definition. However, if we define the funtion F (x) s the definite integrl then we hve F (x) x [ F x+h (x) lim f(s) ds h h i f(s) ds, x f(s) ds h x+h x f(s) ds. Intuitively, s h, this expression onverges to the re of retngle of width h nd height f(x), divided by the width, whih is simply the height, f(x). Tht is, F (x) f(x). This leds to the Fundmentl Theorem of Clulus, whih sttes tht b f(x) dx F (b) F (), where F is n ntiderivtive of f; tht is, F f. Therefore, definite integrls re typilly evluted by ttempting to undo the differentition proess to find n ntiderivtive of the integrnd f(x), nd then evluting this ntiderivtive t nd b, the limits of the integrl. Now, let f(x, y) be funtion of two vribles. We onsider the problem of omputing the volume of the solid in 3-D spe bounded by the surfe z f(x, y), nd the plnes x, x b,
2 y, y d, nd z, where, b, nd d re onstnts. As before, we divide the intervl [, b into n subintervls of width Δx (b )/n, nd we similrly divide the intervl [, d into m subintervls of width Δy (d )/m. For onveniene, we lso define x i + iδx, nd y j + jδy. Then, we n pproximte the volume V of this solid by the sum of the volumes of mn boxes. The bse of eh box is retngle with dimensions Δx nd Δy, nd the height is given by f(x i, y j ), where, for eh i nd j, x i x i x i nd y j yj y j. Tht is, V f(x i, yj ) Δy Δx. i j We then obtin the ext volume of this solid by letting the number of subintervls, n, tend to infinity. The result is the double integrl of f(x, y) over the retngle {(x, y) x b, y d}, whih is lso written s [, b [, d. The double integrl is defined to be V f(x, y) da lim m, i j f(x i, yj ) Δy Δx, whih is equl to the volume of the given solid. The da orresponds to the quntity ΔA ΔxΔy, nd emphsizes the ft tht the integrl is defined to be the limit of the sum of volumes of boxes, eh with bse of re ΔA. To evlute double integrls of this form, we n proeed s in the single-vrible se, by noting tht if f(x, y), funtion of y, is integrble on [, d for eh x [, b, then we hve f(x, y) da lim m, lim lim i j lim i i b d f(x i, yj ) Δy Δx m j f(x i, yj )Δy Δx [ d f(x i, y) dy Δx Similrly, if f(x, y ), funtion of x, is integrble on [, b for eh y [, d, we lso hve f(x, y) da d b
3 This result is known s Fubini s Theorem, whih sttes tht double integrl of funtion f(x, y) n be evluted s two iterted single integrls, provided tht f is integrble s funtion of either vrible when the other vrible is held fixed. This is gurnteed if, for instne, f(x, y) is ontinuous on the entire retngle. Tht is, we n evlute double integrl by performing prtil integrtion with respet to either vrible, x or y, whih entils pplying the Fundmentl Theorem of Clulus to integrte f(x, y) with respet to only tht vrible, while treting the other vrible s onstnt. The result will be funtion of only the other vrible, to whih the Fundmentl Theorem of Clulus n be pplied seond time to omplete the evlution of the double integrl. Exmple Let [, [,, nd let f(x, y) x y + xy 3. We will use Fubini s Theorem to evlute We hve f(x, y) dy dx 8 3. x y + xy 3 dy dx x y + xy 3 dy dx x y dy + [x y dy + x [ x y + x y4 4 dx ( x 3 x + 4x dx 3 + x ) xy 3 dy dx y 3 dy dx In view of Fubini s Theorem, double integrl is often written s f(x, y) da f(x, y) dy dx f(x, y) dx dy. 3
4 Exmple We wish to ompute the volume V of the solid bounded by the plnes x, x 4, y, y, z, nd x + y + z 8. The plne tht defines the top of this solid is lso the grph of the funtion z f(x, y) 8 x y. It follows tht the volume of the solid is given by the double integrl V 8 x y da, [, 4 [,. Using Fubini s Theorem, we obtin V 8 x y da 8 x y dy dx (8y xy y 4 x dx (4x x ) 4 (56 6) (4 ) 7. ) dx We onlude by noting some useful properties of the double integrl, tht re diret generliztions of orresponding properties for single integrls: Linerity: If f(x, y) nd g(x, y) re both integrble over, then [f(x, y) + g(x, y) da f(x, y) da + Homogeneity: If is onstnt, then f(x, y) da Monotoniity: If f(x, y) on, then f(x, y) da. f(x, y) da g(x, y) da Additivity: If nd re disjoint retngles nd Q is retngle, then f(x, y) da f(x, y) da + f(x, y) da. Q 4
5 Prtie Problems. Evlute the following double integrls. () (b) () e x os y da, [, [, π/ e x+y, [, [, ln os(x + y), [, π/4 [, π/4 Hint: try using trigonometri identity to mke it esier to pply Fubini s Theorem.. Compute the volumes of the following solids bounded by the indited surfes. () x, x 3, y, y 4, z, x + y + z 9 (b) x, x, y, y, z, z y os ( ) πx Hint: use the properties of integrls on the previous pge. () x, y, y 4, z, z 4 x Additionl Prtie Problems Additionl prtie problems from the reommended textbooks re: Stewrt: Setion., Exerises -33 odd Mrsden/Tromb: Setion 5., Exerises, 3, 7 5
Lecture 16. Double integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Multivariable integration. Multivariable integration. Iterated integration
 Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Vector Calculus. 1 Line Integrals
 Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Lecture 20. Intro to line integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES
 At Mth Univ Comenine Vol LXXXV, (06, pp 07 07 NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES G FARID Abstrt In this pper, new Ostrowski-type inequlities in two oordintes re estblished
At Mth Univ Comenine Vol LXXXV, (06, pp 07 07 NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES G FARID Abstrt In this pper, new Ostrowski-type inequlities in two oordintes re estblished
Chapter 12 Vectors and the Geometry of Space 12.1 Three-dimensional Coordinate systems
 hpter 12 Vectors nd the Geometry of Spce 12.1 Three-dimensionl oordinte systems A. Three dimensionl Rectngulr oordinte Sydstem: The rtesin product where (x, y, z) isclled ordered triple. B. istnce: R 3
hpter 12 Vectors nd the Geometry of Spce 12.1 Three-dimensionl oordinte systems A. Three dimensionl Rectngulr oordinte Sydstem: The rtesin product where (x, y, z) isclled ordered triple. B. istnce: R 3
Section 16.3 Double Integrals over General Regions
 Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
b = and their properties: b 1 b 2 b 3 a b is perpendicular to both a and 1 b = x = x 0 + at y = y 0 + bt z = z 0 + ct ; y = y 0 )
 ***************** Disclimer ***************** This represents very brief outline of most of the topics covered MA261 *************************************************** I. Vectors, Lines nd Plnes 1. Vector
***************** Disclimer ***************** This represents very brief outline of most of the topics covered MA261 *************************************************** I. Vectors, Lines nd Plnes 1. Vector
Fubini for continuous functions over intervals
 Fuini for ontinuous funtions over intervls We first prove the following theorem for ontinuous funtions. Theorem. Let f(x) e ontinuous on ompt intervl =[, [,. Then [, [, [ [ f(x, y)(x, y) = f(x, y)y x =
Fuini for ontinuous funtions over intervls We first prove the following theorem for ontinuous funtions. Theorem. Let f(x) e ontinuous on ompt intervl =[, [,. Then [, [, [ [ f(x, y)(x, y) = f(x, y)y x =
Section 17.2: Line Integrals. 1 Objectives. 2 Assignments. 3 Maple Commands. 1. Compute line integrals in IR 2 and IR Read Section 17.
 Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
(1) Primary Trigonometric Ratios (SOH CAH TOA): Given a right triangle OPQ with acute angle, we have the following trig ratios: ADJ
 Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
Example. Check that the Jacobian of the transformation to spherical coordinates is
 lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
10.4 AREAS AND LENGTHS IN POLAR COORDINATES
 65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
Double Integrals over More General Regions
 Jim Lambers MAT 8 Spring Semester 9-1 Lecture 11 Notes These notes correspond to Section 1. in Stewart and Sections 5.3 and 5.4 in Marsden and Tromba. ouble Integrals over More General Regions We have
Jim Lambers MAT 8 Spring Semester 9-1 Lecture 11 Notes These notes correspond to Section 1. in Stewart and Sections 5.3 and 5.4 in Marsden and Tromba. ouble Integrals over More General Regions We have
Math 116 Calculus II
 Mth 6 Clculus II Contents 7 Additionl topics in Integrtion 7. Integrtion by prts..................................... 7.4 Numericl Integrtion.................................... 7 7.5 Improper Integrl......................................
Mth 6 Clculus II Contents 7 Additionl topics in Integrtion 7. Integrtion by prts..................................... 7.4 Numericl Integrtion.................................... 7 7.5 Improper Integrl......................................
9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations
 54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
VECTOR CALCULUS Julian.O 2016
 VETO ALULUS Julian.O 2016 Vector alculus Lecture 3: Double Integrals Green s Theorem Divergence of a Vector Field Double Integrals: Double integrals are used to integrate two-variable functions f(x, y)
VETO ALULUS Julian.O 2016 Vector alculus Lecture 3: Double Integrals Green s Theorem Divergence of a Vector Field Double Integrals: Double integrals are used to integrate two-variable functions f(x, y)
Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world
 Person Edution Limited Edinurgh Gte Hrlow Essex M20 2JE Englnd nd ssoited ompnies throughout the world Visit us on the World Wide We t: www.personed.o.uk Person Edution Limited 2014 ll rights reserved.
Person Edution Limited Edinurgh Gte Hrlow Essex M20 2JE Englnd nd ssoited ompnies throughout the world Visit us on the World Wide We t: www.personed.o.uk Person Edution Limited 2014 ll rights reserved.
STUDY GUIDE, CALCULUS III, 2017 SPRING
 TUY GUIE, ALULU III, 2017 PING ontents hpter 13. Functions of severl vribles 1 13.1. Plnes nd surfces 2 13.2. Grphs nd level curves 2 13.3. Limit of function of two vribles 2 13.4. Prtil derivtives 2 13.5.
TUY GUIE, ALULU III, 2017 PING ontents hpter 13. Functions of severl vribles 1 13.1. Plnes nd surfces 2 13.2. Grphs nd level curves 2 13.3. Limit of function of two vribles 2 13.4. Prtil derivtives 2 13.5.
Notes on Spherical Triangles
 Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
13.1 Double Integral over Rectangle. f(x ij,y ij ) i j I <ɛ. f(x, y)da.
 CHAPTE 3, MULTIPLE INTEGALS Definition. 3. Double Integrl over ectngle A function f(x, y) is integrble on rectngle [, b] [c, d] if there is number I such tht for ny given ɛ>0thereisδ>0 such tht, fir ny
CHAPTE 3, MULTIPLE INTEGALS Definition. 3. Double Integrl over ectngle A function f(x, y) is integrble on rectngle [, b] [c, d] if there is number I such tht for ny given ɛ>0thereisδ>0 such tht, fir ny
Patterns and Algebra
 Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Polar Coordinates. July 30, 2014
 Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Study Guide # Vectors in R 2 and R 3. (a) v = a, b, c = a i + b j + c k; vector addition and subtraction geometrically using parallelograms
 Study Guide # 1 MA 26100 - Fll 2018 1. Vectors in R 2 nd R 3 () v =, b, c = i + b j + c k; vector ddition nd subtrction geometriclly using prllelogrms spnned by u nd v; length or mgnitude of v =, b, c,
Study Guide # 1 MA 26100 - Fll 2018 1. Vectors in R 2 nd R 3 () v =, b, c = i + b j + c k; vector ddition nd subtrction geometriclly using prllelogrms spnned by u nd v; length or mgnitude of v =, b, c,
Section 6.1 Law of Sines. Notes. Oblique Triangles - triangles that have no right angles. A c. A is acute. A is obtuse
 Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Estimating Areas. is reminiscent of a Riemann Sum and, amazingly enough, will be called a Riemann Sum. Double Integrals
 Estimating Areas Consider the challenge of estimating the volume of a solid {(x, y, z) 0 z f(x, y), (x, y) }, where is a region in the xy-plane. This may be thought of as the solid under the graph of z
Estimating Areas Consider the challenge of estimating the volume of a solid {(x, y, z) 0 z f(x, y), (x, y) }, where is a region in the xy-plane. This may be thought of as the solid under the graph of z
Macroscopic and Microscopic Springs Procedure
 Mrosopi nd Mirosopi Springs Proedure OBJECTIVE Purpose In this l you will: investigte the spring-like properties of stright wire, disover the strethiness of mteril, independent of the size nd shpe of n
Mrosopi nd Mirosopi Springs Proedure OBJECTIVE Purpose In this l you will: investigte the spring-like properties of stright wire, disover the strethiness of mteril, independent of the size nd shpe of n
Samantha s Strategies page 1 of 2
 Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Abdominal Wound Closure Forceps
 Inventor: Crlson, Mrk A. My 25, 2007 Adominl Wound Closure Foreps Astrt. The devie is modifition of stndrd tissue foreps for use during losure of dominl wounds mde for surgil proedure. The modifition onsists
Inventor: Crlson, Mrk A. My 25, 2007 Adominl Wound Closure Foreps Astrt. The devie is modifition of stndrd tissue foreps for use during losure of dominl wounds mde for surgil proedure. The modifition onsists
WI1402-LR Calculus II Delft University of Technology
 WI402-LR lculus II elft University of Technology Yer 203 204 Michele Fcchinelli Version.0 Lst modified on Februry, 207 Prefce This summry ws written for the course WI402-LR lculus II, tught t the elft
WI402-LR lculus II elft University of Technology Yer 203 204 Michele Fcchinelli Version.0 Lst modified on Februry, 207 Prefce This summry ws written for the course WI402-LR lculus II, tught t the elft
33. Riemann Summation over Rectangular Regions
 . iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
. iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
INTEGRATION OVER NON-RECTANGULAR REGIONS. Contents 1. A slightly more general form of Fubini s Theorem
 INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
Multiple Integrals. Advanced Calculus. Lecture 1 Dr. Lahcen Laayouni. Department of Mathematics and Statistics McGill University.
 Lecture epartment of Mathematics and Statistics McGill University January 4, 27 ouble integrals Iteration of double integrals ouble integrals Consider a function f(x, y), defined over a rectangle = [a,
Lecture epartment of Mathematics and Statistics McGill University January 4, 27 ouble integrals Iteration of double integrals ouble integrals Consider a function f(x, y), defined over a rectangle = [a,
REVIEW QUESTIONS TOPIC 5 TRIGONOMETRY I FLUENCY
 TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES
 MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Exercise 1-1. The Sine Wave EXERCISE OBJECTIVE DISCUSSION OUTLINE. Relationship between a rotating phasor and a sine wave DISCUSSION
 Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY
 LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
Functions of several variables
 Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Unit 1: Chapter 4 Roots & Powers
 Unit 1: Chpter 4 Roots & Powers Big Ides Any number tht cn be written s the frction mm, nn 0, where m nd n re integers, is nn rtionl. Eponents cn be used to represent roots nd reciprocls of rtionl numbers.
Unit 1: Chpter 4 Roots & Powers Big Ides Any number tht cn be written s the frction mm, nn 0, where m nd n re integers, is nn rtionl. Eponents cn be used to represent roots nd reciprocls of rtionl numbers.
Calculus IV Math 2443 Review for Exam 2 on Mon Oct 24, 2016 Exam 2 will cover This is only a sample. Try all the homework problems.
 Calculus IV Math 443 eview for xam on Mon Oct 4, 6 xam will cover 5. 5.. This is only a sample. Try all the homework problems. () o not evaluated the integral. Write as iterated integrals: (x + y )dv,
Calculus IV Math 443 eview for xam on Mon Oct 4, 6 xam will cover 5. 5.. This is only a sample. Try all the homework problems. () o not evaluated the integral. Write as iterated integrals: (x + y )dv,
EE (082) Chapter IV: Angle Modulation Lecture 21 Dr. Wajih Abu-Al-Saud
 EE 70- (08) Chapter IV: Angle Modulation Leture Dr. Wajih Abu-Al-Saud Effet of Non Linearity on AM and FM signals Sometimes, the modulated signal after transmission gets distorted due to non linearities
EE 70- (08) Chapter IV: Angle Modulation Leture Dr. Wajih Abu-Al-Saud Effet of Non Linearity on AM and FM signals Sometimes, the modulated signal after transmission gets distorted due to non linearities
F13 Study Guide/Practice Exam 3
 F13 Study Guide/Practice Exam 3 This study guide/practice exam covers only the material since exam 2. The final exam, however, is cumulative so you should be sure to thoroughly study earlier material.
F13 Study Guide/Practice Exam 3 This study guide/practice exam covers only the material since exam 2. The final exam, however, is cumulative so you should be sure to thoroughly study earlier material.
Independent of path Green s Theorem Surface Integrals. MATH203 Calculus. Dr. Bandar Al-Mohsin. School of Mathematics, KSU 20/4/14
 School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Evaluating territories of Go positions with capturing races
 Gmes of No Chne 4 MSRI Pulitions Volume 63, 2015 Evluting territories of Go positions with pturing res TEIGO NAKAMURA In nlysing pturing res, or semeis, we hve een fousing on the method to find whih plyer
Gmes of No Chne 4 MSRI Pulitions Volume 63, 2015 Evluting territories of Go positions with pturing res TEIGO NAKAMURA In nlysing pturing res, or semeis, we hve een fousing on the method to find whih plyer
Spherical Geometry. This is an article from my home page:
 Spheril Geometry This is n rtile from my home pge: www.olewitthnsen.dk Ole Witt-Hnsen nov. 6 Contents. Geometry on sphere.... Spheril tringles...3. Polr tringles...4 3. The right-ngle spheril tringle...6
Spheril Geometry This is n rtile from my home pge: www.olewitthnsen.dk Ole Witt-Hnsen nov. 6 Contents. Geometry on sphere.... Spheril tringles...3. Polr tringles...4 3. The right-ngle spheril tringle...6
Version of 7. , using 30 points from 5 rad/s to 5 krad/s. Paste your plot below. Remember to label your plot.
 Version 1.2 1 of 7 Your Name Passive and Ative Filters Date ompleted PELAB MATLAB = 1000 s + 1000, using 30 points from 5 rad/s to 5 krad/s. Paste your plot below. emember to label your plot. 1. reate
Version 1.2 1 of 7 Your Name Passive and Ative Filters Date ompleted PELAB MATLAB = 1000 s + 1000, using 30 points from 5 rad/s to 5 krad/s. Paste your plot below. emember to label your plot. 1. reate
Computational Complexity of a Pop-up Book
 omputtionl omplexity of Pop-up ook Ryuhei Uehr Shio Termoto strt Origmi is the enturies-ol rt of foling pper, n reently, it is investigte s omputer siene: Given n origmi ith reses, the prolem to etermine
omputtionl omplexity of Pop-up ook Ryuhei Uehr Shio Termoto strt Origmi is the enturies-ol rt of foling pper, n reently, it is investigte s omputer siene: Given n origmi ith reses, the prolem to etermine
Geometric quantities for polar curves
 Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Comparing Fractions page 1 of 2 1 Color in the grid to show the fractions below. Each grid represents 1 whole. a 1 2 b 1. d 16
 Unit 2 Moule Session 2 Compring Frtions pge of 2 Color in the gri to show the frtions below. Eh gri represents whole. 2 b 4 0 0 e 4 2 Use the pitures bove to help omplete eh omprison below using ,
Unit 2 Moule Session 2 Compring Frtions pge of 2 Color in the gri to show the frtions below. Eh gri represents whole. 2 b 4 0 0 e 4 2 Use the pitures bove to help omplete eh omprison below using ,
GLONASS PhaseRange biases in RTK processing
 ASS PhseRnge ises in RTK proessing Gle Zyrynov Ashteh Workshop on GSS Bises 202 Bern Switzerlnd Jnury 8-9 202 Sope Simplified oservtion models for Simplified oservtion models for ASS FDMA speifi: lok nd
ASS PhseRnge ises in RTK proessing Gle Zyrynov Ashteh Workshop on GSS Bises 202 Bern Switzerlnd Jnury 8-9 202 Sope Simplified oservtion models for Simplified oservtion models for ASS FDMA speifi: lok nd
Power Budgeted Packet Scheduling for Wireless Multimedia
 Power Budgeted Paket Sheduling for Wireless Multimedia Praveen Bommannavar Management Siene and Engineering Stanford University Stanford, CA 94305 USA bommanna@stanford.edu Niholas Bambos Eletrial Engineering
Power Budgeted Paket Sheduling for Wireless Multimedia Praveen Bommannavar Management Siene and Engineering Stanford University Stanford, CA 94305 USA bommanna@stanford.edu Niholas Bambos Eletrial Engineering
CS 135: Computer Architecture I. Boolean Algebra. Basic Logic Gates
 Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Understanding Three-Phase Transformers
 PDH ourse E450 (4 PDH) Understnding Three-Phse Trnsformers Rlph Fehr, Ph.D., P.E. 2014 PDH Online PDH enter 5272 Medow Esttes Drive Firfx, V 22030-6658 Phone & Fx: 703-988-0088 www.pdhonline.org www.pdhenter.om
PDH ourse E450 (4 PDH) Understnding Three-Phse Trnsformers Rlph Fehr, Ph.D., P.E. 2014 PDH Online PDH enter 5272 Medow Esttes Drive Firfx, V 22030-6658 Phone & Fx: 703-988-0088 www.pdhonline.org www.pdhenter.om
Reprint from IASTED International Conference on Signal and Image Processing (SIP 99). Nassau, Bahamas, October, 1999.
 Reprint from IASTED International Conferene on Signal and Image Proessing (SIP 99). Nassau, Bahamas, Otober, 1999. 1 Filter Networks Mats Andersson Johan Wiklund Hans Knutsson Computer Vision Laboratory,
Reprint from IASTED International Conferene on Signal and Image Proessing (SIP 99). Nassau, Bahamas, Otober, 1999. 1 Filter Networks Mats Andersson Johan Wiklund Hans Knutsson Computer Vision Laboratory,
University of California, Berkeley Department of Mathematics 5 th November, 2012, 12:10-12:55 pm MATH 53 - Test #2
 University of California, Berkeley epartment of Mathematics 5 th November, 212, 12:1-12:55 pm MATH 53 - Test #2 Last Name: First Name: Student Number: iscussion Section: Name of GSI: Record your answers
University of California, Berkeley epartment of Mathematics 5 th November, 212, 12:1-12:55 pm MATH 53 - Test #2 Last Name: First Name: Student Number: iscussion Section: Name of GSI: Record your answers
This exam contains 9 problems. CHECK THAT YOU HAVE A COMPLETE EXAM.
 Math 126 Final Examination Winter 2012 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name This exam contains 9 problems. CHECK THAT YOU HAVE A COMPLETE EXAM. This exam is closed
Math 126 Final Examination Winter 2012 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name This exam contains 9 problems. CHECK THAT YOU HAVE A COMPLETE EXAM. This exam is closed
Spiral Tilings with C-curves
 Spirl Tilings with -curves Using ombintorics to Augment Trdition hris K. Plmer 19 North Albny Avenue hicgo, Illinois, 0 chris@shdowfolds.com www.shdowfolds.com Abstrct Spirl tilings used by rtisns through
Spirl Tilings with -curves Using ombintorics to Augment Trdition hris K. Plmer 19 North Albny Avenue hicgo, Illinois, 0 chris@shdowfolds.com www.shdowfolds.com Abstrct Spirl tilings used by rtisns through
FP2 POLAR COORDINATES: PAST QUESTIONS
 FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
Calculating the input-output dynamic characteristics. Analyzing dynamic systems and designing controllers.
 CHAPTER : REVIEW OF FREQUENCY DOMAIN ANALYSIS The long-term response of a proess is nown as the frequeny response whih is obtained from the response of a omplex-domain transfer funtion. The frequeny response
CHAPTER : REVIEW OF FREQUENCY DOMAIN ANALYSIS The long-term response of a proess is nown as the frequeny response whih is obtained from the response of a omplex-domain transfer funtion. The frequeny response
IMAGE PROCESSING (RRY025) THE CONTINUOUS 2D FOURIER TRANSFORM
 IMAGE PROCESSING (RRY5) THE CONTINUOUS D FOURIER TRANSFORM INTRODUCTION A vital tool in image processing. Also a prototype of other image transforms, cosine, Wavelet etc. Applications Image Filtering -
IMAGE PROCESSING (RRY5) THE CONTINUOUS D FOURIER TRANSFORM INTRODUCTION A vital tool in image processing. Also a prototype of other image transforms, cosine, Wavelet etc. Applications Image Filtering -
(CATALYST GROUP) B"sic Electric"l Engineering
 (CATALYST GROUP) B"sic Electric"l Engineering 1. Kirchhoff s current l"w st"tes th"t (") net current flow "t the junction is positive (b) Hebr"ic sum of the currents meeting "t the junction is zero (c)
(CATALYST GROUP) B"sic Electric"l Engineering 1. Kirchhoff s current l"w st"tes th"t (") net current flow "t the junction is positive (b) Hebr"ic sum of the currents meeting "t the junction is zero (c)
8.1. The Sine Law. Investigate. Tools
 8.1 Te Sine Lw Mimi 50 ermud Tringle ermud 1600 km Sn Jun 74 Puerto Rio Te ermud Tringle, in te nort tlnti Oen, is te lotion of severl unexplined plne nd sip disppernes. Vrious teories ve een suggested
8.1 Te Sine Lw Mimi 50 ermud Tringle ermud 1600 km Sn Jun 74 Puerto Rio Te ermud Tringle, in te nort tlnti Oen, is te lotion of severl unexplined plne nd sip disppernes. Vrious teories ve een suggested
Module 5 Carrier Modulation. Version 2 ECE IIT, Kharagpur
 Module 5 Carrier Modulation Version ECE II, Kharagpur Lesson 5 Quaternary Phase Shift Keying (QPSK) Modulation Version ECE II, Kharagpur After reading this lesson, you will learn about Quaternary Phase
Module 5 Carrier Modulation Version ECE II, Kharagpur Lesson 5 Quaternary Phase Shift Keying (QPSK) Modulation Version ECE II, Kharagpur After reading this lesson, you will learn about Quaternary Phase
REVIEW QUESTIONS. Figure For Review Question Figure For Review Question Figure For Review Question 10.2.
 HAPTE 0 Sinusoidl Stedy-Stte Anlysis 42 EVIEW QUESTIONS 0. The voltge cross the cpcitor in Fig. 0.43 is: () 5 0 V () 7.07 45 V (c) 7.07 45 V (d) 5 45 V Ω 0.5 efer to the circuit in Fig. 0.47 nd oserve
HAPTE 0 Sinusoidl Stedy-Stte Anlysis 42 EVIEW QUESTIONS 0. The voltge cross the cpcitor in Fig. 0.43 is: () 5 0 V () 7.07 45 V (c) 7.07 45 V (d) 5 45 V Ω 0.5 efer to the circuit in Fig. 0.47 nd oserve
MATH Exam 2 Solutions November 16, 2015
 MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
Defining the Rational Numbers
 MATH10 College Mthemtis - Slide Set 2 1. Rtionl Numers 1. Define the rtionl numers. 2. Redue rtionl numers.. Convert etween mixed numers nd improper frtions. 4. Express rtionl numers s deimls.. Express
MATH10 College Mthemtis - Slide Set 2 1. Rtionl Numers 1. Define the rtionl numers. 2. Redue rtionl numers.. Convert etween mixed numers nd improper frtions. 4. Express rtionl numers s deimls.. Express
Polar coordinates 5C. 1 a. a 4. π = 0 (0) is a circle centre, 0. and radius. The area of the semicircle is π =. π a
 Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
14.2 Limits and Continuity
 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
Switching Algorithms for the Dual Inverter fed Open-end Winding Induction Motor Drive for 3-level Voltage Space Phasor Generation
 S.Srinivs et l: Swithing Algorithms for the Dul Inverter fed... Swithing Algorithms for the Dul Inverter fed Open-end Winding Indution Motor Drive for 3-level Voltge Spe Phsor Genertion S. Srinivs nd V..
S.Srinivs et l: Swithing Algorithms for the Dul Inverter fed... Swithing Algorithms for the Dul Inverter fed Open-end Winding Indution Motor Drive for 3-level Voltge Spe Phsor Genertion S. Srinivs nd V..
ICL7116, ICL / 2 Digit, LCD/LED Display, A/D Converter with Display Hold. Description. Features. Ordering Information. Pinouts.
 SEMICONDUCTOR ICL116, ICL11 August 199 3 1 / 2 Digit, LCD/LED Disply, A/D Converter with Disply Hold Fetures HOLD Reding Input Allows Indefinite Disply Hold Gurnteed Zero Reding for 0V Input True Polrity
SEMICONDUCTOR ICL116, ICL11 August 199 3 1 / 2 Digit, LCD/LED Disply, A/D Converter with Disply Hold Fetures HOLD Reding Input Allows Indefinite Disply Hold Gurnteed Zero Reding for 0V Input True Polrity
Differentiable functions (Sec. 14.4)
 Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Review guide for midterm 2 in Math 233 March 30, 2009
 Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Positron Emission Tomography (PET) Images
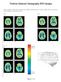 Positron Emission Tomogrphy (PET) Imges Eh set of PET imges elow ontins four imges of humn rin. The four imges show ross-setions tken t ifferent levels of the rin. Set 1 Set 4 Set 5 Set 2 Set 6 Set 3 highest
Positron Emission Tomogrphy (PET) Imges Eh set of PET imges elow ontins four imges of humn rin. The four imges show ross-setions tken t ifferent levels of the rin. Set 1 Set 4 Set 5 Set 2 Set 6 Set 3 highest
SLOVAK UNIVERSITY OF TECHNOLOGY Faculty of Material Science and Technology in Trnava. ELECTRICAL ENGINEERING AND ELECTRONICS Laboratory exercises
 SLOVAK UNIVERSITY OF TECHNOLOGY Fulty of Mteril Siene nd Tehnology in Trnv ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory exerises Róbert Riedlmjer TRNAVA 00 ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory
SLOVAK UNIVERSITY OF TECHNOLOGY Fulty of Mteril Siene nd Tehnology in Trnv ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory exerises Róbert Riedlmjer TRNAVA 00 ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory
Applications of a New Property of Conics to Architecture: An Alternative Design Project for Rio de Janeiro Metropolitan Cathedral
 Jun V. Mrtín Zorrquino Frneso Grnero odrígue José uis Cno Mrtín Applitions of New Property of Conis to Arhiteture: An Alterntive Design Projet for io de Jneiro Metropolitn Cthedrl This pper desries the
Jun V. Mrtín Zorrquino Frneso Grnero odrígue José uis Cno Mrtín Applitions of New Property of Conis to Arhiteture: An Alterntive Design Projet for io de Jneiro Metropolitn Cthedrl This pper desries the
by Kathy Brown of The Teacher s Pet
 y Kthy Brown of The Teher s Pet Designs y Kthy Brown Pieing y Kthy Brown & Lin Ree Mhine quilte y Crol Hilton www.reroosterfris.om Quilte size: pproximtely 40" x 50" Fris from the Sprinkles (Style #4527)
y Kthy Brown of The Teher s Pet Designs y Kthy Brown Pieing y Kthy Brown & Lin Ree Mhine quilte y Crol Hilton www.reroosterfris.om Quilte size: pproximtely 40" x 50" Fris from the Sprinkles (Style #4527)
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN. Inventor: Brian L. Baskin
 METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
Domination and Independence on Square Chessboard
 Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
ISM-PRO SOFTWARE DIGITAL MICROSCOPE OPERATION MANUAL
 MN-ISM-PRO-E www.insize.om ISM-PRO SOFTWARE DIGITAL MICROSCOPE OPERATION MANUAL Desription Clik Next. As the following piture: ISM-PRO softwre is for ISM-PM00SA, ISM-PM600SA, ISM- PM60L digitl mirosopes.
MN-ISM-PRO-E www.insize.om ISM-PRO SOFTWARE DIGITAL MICROSCOPE OPERATION MANUAL Desription Clik Next. As the following piture: ISM-PRO softwre is for ISM-PM00SA, ISM-PM600SA, ISM- PM60L digitl mirosopes.
University of North Carolina-Charlotte Department of Electrical and Computer Engineering ECGR 4143/5195 Electrical Machinery Fall 2009
 Problem 1: Using DC Mchine University o North Crolin-Chrlotte Deprtment o Electricl nd Computer Engineering ECGR 4143/5195 Electricl Mchinery Fll 2009 Problem Set 4 Due: Thursdy October 8 Suggested Reding:
Problem 1: Using DC Mchine University o North Crolin-Chrlotte Deprtment o Electricl nd Computer Engineering ECGR 4143/5195 Electricl Mchinery Fll 2009 Problem Set 4 Due: Thursdy October 8 Suggested Reding:
The Nottingham eprints service makes this work by researchers of the University of Nottingham available open access under the following conditions.
 Remenyte-Presott, Rs nd Andrews, John (27) Prime implints for modulrised non-oherent fult trees using inry deision digrms. Interntionl Journl of Reliility nd Sfety, (4). pp. 446-464. ISSN 479-393 Aess
Remenyte-Presott, Rs nd Andrews, John (27) Prime implints for modulrised non-oherent fult trees using inry deision digrms. Interntionl Journl of Reliility nd Sfety, (4). pp. 446-464. ISSN 479-393 Aess
Balancing Your Life. Ideas that might help you
 Blning Your Life Ides tht might help you Pul Hoskin Summer 2007 Let s e honest if one lists off the responsiilities nd hoies tht eh of us hve nd ssigns weekly hourly time tht eh needs to e fulfilled, then
Blning Your Life Ides tht might help you Pul Hoskin Summer 2007 Let s e honest if one lists off the responsiilities nd hoies tht eh of us hve nd ssigns weekly hourly time tht eh needs to e fulfilled, then
MATH 105: Midterm #1 Practice Problems
 Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Resistors, Current and Voltage measurements, Ohm s law, Kirchhoff s first and second law. Kirchhoff s first Objectives:
 EE -050 Ciruit L Experiment # esistors, Current nd Voltge mesurements, Ohm s lw, Kirhhoff s first nd seond lw. Kirhhoff s first Ojetives: Slmn in Adul Aziz University Eletril Engineering Deprtment. Fmiliriztion
EE -050 Ciruit L Experiment # esistors, Current nd Voltge mesurements, Ohm s lw, Kirhhoff s first nd seond lw. Kirhhoff s first Ojetives: Slmn in Adul Aziz University Eletril Engineering Deprtment. Fmiliriztion
NUMBER THEORY Amin Witno
 WON Series in Discrete Mthemtics nd Modern Algebr Volume 2 NUMBER THEORY Amin Witno Prefce Written t Phildelphi University, Jordn for Mth 313, these notes 1 were used first time in the Fll 2005 semester.
WON Series in Discrete Mthemtics nd Modern Algebr Volume 2 NUMBER THEORY Amin Witno Prefce Written t Phildelphi University, Jordn for Mth 313, these notes 1 were used first time in the Fll 2005 semester.
Energy Harvesting Two-Way Channels With Decoding and Processing Costs
 IEEE TRANSACTIONS ON GREEN COMMUNICATIONS AND NETWORKING, VOL., NO., MARCH 07 3 Energy Hrvesting Two-Wy Chnnels With Decoding nd Processing Costs Ahmed Arf, Student Member, IEEE, Abdulrhmn Bknin, Student
IEEE TRANSACTIONS ON GREEN COMMUNICATIONS AND NETWORKING, VOL., NO., MARCH 07 3 Energy Hrvesting Two-Wy Chnnels With Decoding nd Processing Costs Ahmed Arf, Student Member, IEEE, Abdulrhmn Bknin, Student
Lecture 22: Digital Transmission Fundamentals
 EE 400: Communiation Networks (0) Ref: A. Leon Garia and I. Widjaja, Communiation Networks, 2 nd Ed. MGraw Hill, 2006 Latest update of this leture was on 30 200 Leture 22: Digital Transmission Fundamentals
EE 400: Communiation Networks (0) Ref: A. Leon Garia and I. Widjaja, Communiation Networks, 2 nd Ed. MGraw Hill, 2006 Latest update of this leture was on 30 200 Leture 22: Digital Transmission Fundamentals
Independence of Path and Conservative Vector Fields
 Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
A Development of Embedded System for Speed Control of Hydraulic Motor
 AISTPME (2011) 4(4): 35-39 A Development of Embedded System for Speed Control of Hydruli Motor Pornjit P. Edutionl Mehtronis Reserh Group Deprtment of Teher Trining in Mehnil Engineering, KMUTN, ngkok,
AISTPME (2011) 4(4): 35-39 A Development of Embedded System for Speed Control of Hydruli Motor Pornjit P. Edutionl Mehtronis Reserh Group Deprtment of Teher Trining in Mehnil Engineering, KMUTN, ngkok,
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
AGA56... Analog Input Modules. Siemens Building Technologies HVAC Products
 7 922 nlog Input odules G56... nlog input modules for the ontrol of SQ5... ir dmper tutors y ontinuous nlog ontrol signls, suh s 4...20 m, nd ontinuous nlog position feedk signls. For supplementry Dt Sheets,
7 922 nlog Input odules G56... nlog input modules for the ontrol of SQ5... ir dmper tutors y ontinuous nlog ontrol signls, suh s 4...20 m, nd ontinuous nlog position feedk signls. For supplementry Dt Sheets,
arxiv: v2 [cs.sy] 16 Nov 2012
![arxiv: v2 [cs.sy] 16 Nov 2012 arxiv: v2 [cs.sy] 16 Nov 2012](/thumbs/86/93861098.jpg) IEEE Personl use of this mteril is permitted Permission from IEEE must e otined for ll other uses, in ny urrent or future medi, inluding reprinting/repulishing this mteril for dvertising or promotionl
IEEE Personl use of this mteril is permitted Permission from IEEE must e otined for ll other uses, in ny urrent or future medi, inluding reprinting/repulishing this mteril for dvertising or promotionl
Math Circles Finite Automata Question Sheet 3 (Solutions)
 Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
COMPUTER MODELLING OF FLICKER PROPAGATION
 OMPUTER MODELLING OF FLIKER PROPGTION T.Keppler N.R.Wtson J.rrillg University of nterury hristhurh, New Zelnd n.wtson@ele.nterury..nz strt The time series of the voltges t the desired lotions re first
OMPUTER MODELLING OF FLIKER PROPGTION T.Keppler N.R.Wtson J.rrillg University of nterury hristhurh, New Zelnd n.wtson@ele.nterury..nz strt The time series of the voltges t the desired lotions re first
MATH 20C: FUNDAMENTALS OF CALCULUS II FINAL EXAM
 MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
Jordi Selga, Student Member IEEE, Ana Rodríguez, Student Member IEEE, Vicente E. Boria, Senior Member IEEE, and Ferran Martín, Fellow IEEE
 Synthesis o Split Rings bsed Artiiil Trnsmission ines through New Two-Step, Fst onverging, nd Robust Aggressive Spe Mpping ASM Algorithm Jordi Selg, Student Member IEEE, An Rodríguez, Student Member IEEE,
Synthesis o Split Rings bsed Artiiil Trnsmission ines through New Two-Step, Fst onverging, nd Robust Aggressive Spe Mpping ASM Algorithm Jordi Selg, Student Member IEEE, An Rodríguez, Student Member IEEE,
ECE 274 Digital Logic Fall 2009 Digital Design
 igitl Logic ll igitl esign MW -:PM, IL Romn Lysecky, rlysecky@ece.rizon.edu http://www.ece.rizon.edu/~ece hpter : Introduction Slides to ccompny the textbook igitl esign, irst dition, by rnk Vhid, John
igitl Logic ll igitl esign MW -:PM, IL Romn Lysecky, rlysecky@ece.rizon.edu http://www.ece.rizon.edu/~ece hpter : Introduction Slides to ccompny the textbook igitl esign, irst dition, by rnk Vhid, John
