9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations

Transcription

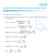
1 54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show tht the polr eqution r sin b cos, where b, represents circle, nd find its center nd rdius. 56. Show tht the curves r sin nd r cos intersect t right ngles. ; 57 6 Use grphing device to grph the polr curve. Choose the prmeter intervl to mke sure tht ou produce the entire curve. 57. r e sin (butterfl curve) cos4 58. r sin 4 cos4 59. r 5 sin6 6. r cos cos3 ; 6. How re the grphs of r sin 6 nd r sin 3 relted to the grph of r sin? In generl, how is the grph of r f relted to the grph of r f? ; 6. Use grph to estimte the -coordinte of the highest points on the curve r sin. Then use clculus to find the exct vlue. ; 63. () Investigte the fmil of curves defined b the polr equtions r sin n, where n is positive integer. How is the number of loops relted to n? (b) Wht hppens if the eqution in prt () is replced b r sin n? ; 64. A fmil of curves is given b the equtions r c sin n, where c is rel number nd n is positive integer. How does the grph chnge s n increses? How does it chnge s c chnges? Illustrte b grphing enough members of the fmil to support our conclusions. 6 ; 65. A fmil of curves hs polr equtions Investigte how the grph chnges s the number chnges. In prticulr, ou should identif the trnsitionl vlues of for which the bsic shpe of the curve chnges. ; 66. The stronomer Giovnni Cssini (65 7) studied the fmil of curves with polr equtions where nd c re positive rel numbers. These curves re clled the ovls of Cssini even though the re ovl shped onl for certin vlues of nd c. (Cssini thought tht these curves might represent plnetr orbits better thn Kepler s ellipses.) Investigte the vriet of shpes tht these curves m hve. In prticulr, how re nd c relted to ech other when the curve splits into two prts? 67. Let P be n point (except the origin) on the curve r f. If is the ngle between the tngent line t P nd the rdil line P, show tht tn r [Hint: bserve tht r 4 c r cos c 4 4 in the figure.] 68. () Use Exercise 67 to show tht the ngle between the tngent line nd the rdil line is t ever point on the curve r e. ; (b) Illustrte prt () b grphing the curve nd the tngent lines t the points where nd. (c) Prove tht n polr curve r f with the propert tht the ngle between the rdil line nd the tngent line is constnt must be of the form r Ce k, where C nd k re constnts. r cos cos r=f( ) drd P ÿ AREAS AND LENGTHS IN PLAR CRDINATES r In this section we develop the formul for the re of region whose boundr is given b polr eqution. We need to use the formul for the re of sector of circle A r FIGURE where, s in Figure, r is the rdius nd is the rdin mesure of the centrl ngle.

2 SECTIN 9.4 AREAS AND LENGTHS IN PLAR CRDINATES 55 =b b FIGURE r=f( ) = f( i*) = i Formul follows from the fct tht the re of sector is proportionl to its centrl ngle: A r r. (See lso Exercise 67 in Section 6..) Let be the region, illustrted in Figure, bounded b the polr curve r f nd b the rs nd, where f is positive continuous function nd where b. We divide the intervl, b into subintervls with endpoints,,,..., n nd equl width. The rs i then divide into n smller regions with centrl ngle i i. If we choose i* in the ith subintervl i, i, then the re A i of the ith region is pproximted b the re of the sector of circle with centrl ngle nd rdius f i*. (See Figure 3.) Thus from Formul we hve b A i f i* nd so n pproximtion to the totl re A of is = i- =b Î = A n i f i* It ppers from Figure 3 tht the pproximtion in () improves s n l. But the sums in () re Riemnn sums for the function t f, so FIGURE 3 lim n l n i f i* b f d It therefore ppers plusible (nd cn in fct be proved) tht the formul for the re A of the polr region is 3 A b f d Formul 3 is often written s 4 A b r d with the understnding tht r f. Note the similrit between Formuls nd 4. When we ppl Formul 3 or 4 it is helpful to think of the re s being swept out b rotting r through tht strts with ngle nd ends with ngle b. r=cos = π 4 V EXAMPLE Find the re enclosed b one loop of the four-leved rose r cos. SLUTIN The curve r cos ws sketched in Exmple 8 in Section 9.3. Notice from Figure 4 tht the region enclosed b the right loop is swept out b r tht rottes from to. Therefore, Formul 4 gives 4 4 FIGURE 4 =_ π 4 4 A 4 4 r d 4 4 cos d cos 4 d 4 cos d [ 4 4 sin 4] 8

3 56 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES = 5π 6 r=3 sin = π 6 V EXAMPLE Find the re of the region tht lies inside the circle r 3 sin nd outside the crdioid r sin. SLUTIN The crdioid (see Exmple 7 in Section 9.3) nd the circle re sketched in Figure 5 nd the desired region is shded. The vlues of nd b in Formul 4 re determined b finding the points of intersection of the two curves. The intersect when 3 sin sin, which gives sin, so, 56. The desired re cn be found b subtrcting the re inside the crdioid between nd from the re inside the circle from 6 to 56. Thus r=+sin A 56 3 sin d 56 sin d 6 6 FIGURE 5 Since the region is smmetric bout the verticl xis, we cn write A 9 sin d sin sin d sin sin d cos sin d 6 [becuse sin cos ] 3 sin cos ]6 =b r=g( ) = FIGURE 6 r=f( ) Exmple illustrtes the procedure for finding the re of the region bounded b two polr curves. In generl, let be region, s illustrted in Figure 6, tht is bounded b curves with polr equtions r f, r t,, nd, where f t nd b. The re A of is found b subtrcting the re inside r t from the re inside r f, so using Formul 3 we hve A b f d b t d b ( f t ) d CAUTIN The fct tht single point hs mn representtions in polr coordintes sometimes mkes it difficult to find ll the points of intersection of two polr curves. For instnce, it is obvious from Figure 5 tht the circle nd the crdioid hve three points of intersection; however, in Exmple we solved the equtions r 3 sin nd r sin nd found onl two such points, ( 3, 6) nd ( 3, 56). The origin is lso point of intersection, but we cn t find it b solving the equtions of the curves becuse the origin hs no single representtion in polr coordintes tht stisfies both equtions. Notice tht, when represented s, or,, the origin stisfies r 3 sin nd so it lies on the circle; when represented s, 3, it stisfies r sin nd so it lies on the crdioid. Think of two points moving long the curves s the prmeter vlue increses from to. n one curve the origin is reched t nd ; on the other curve it is reched t. The points don t collide t the origin becuse the rech the origin t different times, but the curves intersect there nonetheless. Thus, to find ll points of intersection of two polr curves, it is recommended tht ou drw the grphs of both curves. It is especill convenient to use grphing clcultor or computer to help with this tsk. 3 b

4 SECTIN 9.4 AREAS AND LENGTHS IN PLAR CRDINATES 57 r= r=cos π, 3 π, 6 EXAMPLE 3 Find ll points of intersection of the curves r cos nd r. SLUTIN If we solve the equtions r cos nd r, we get cos nd, therefore, 3, 53, 73, 3. Thus the vlues of between nd tht stisf both equtions re 6, 56, 76, 6. We hve found four points of intersection: (, 6), (, 56), (, 76), nd (, 6). However, ou cn see from Figure 7 tht the curves hve four other points of intersection nmel, (, 3), (, 3), (, 43), nd (, 53). These cn be found using smmetr or b noticing tht nother eqution of the circle is r nd then solving the equtions r cos nd r. FIGURE 7 ARC LENGTH b To find the length of polr curve r f,, we regrd s prmeter nd write the prmetric equtions of the curve s x r cos f cos r sin f sin Using the Product Rule nd differentiting with respect to, we obtin dx d dr d cos r sin d d dr d sin r cos FIGURE 8 r=+sin so, using cos sin, we hve dx d d d dr cos d r dr cos sin r sin d dr sin r dr sin cos r cos dr r Assuming tht f is continuous, we cn use Formul 9..5 to write the rc length s Therefore, the length of curve with polr eqution r f,, is 5 d L b b L r d dr V EXAMPLE 4 Find the length of the crdioid r sin. d dx d d SLUTIN The crdioid is shown in Figure 8. (We sketched it in Exmple 7 in Section 9.3.) Its full length is given b the prmeter intervl, so d d d d b

5 58 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES Formul 5 gives L r s sin d dr d d We could evlute this integrl b multipling nd dividing the integrnd b s sin, or we could use computer lgebr sstem. In n event, we find tht the length of the crdioid is L 8. s sin cos d 9.4 EXERCISES 4 Find the re of the region tht is bounded b the given curve nd lies in the specified sector.. r s,. r e, 3. r sin, 4. r ssin, Find the re of the shded region Find the re of the region enclosed b one loop of the curve. 5. r sin 6. r 4 sin 3 7. r sin (inner loop) 8. 9 Find the re of the region tht lies inside the first curve nd outside the second curve. 9. r 4 sin,. r sin,. r 3 cos, r r r cos r cos sec. r sin, r 3 sin 3 6 Find the re of the region tht lies inside both curves. r= r=+sin 3. r sin, r cos 4. r sin, r sin r sin, r cos 6. r sin, r 7. Find the re inside the lrger loop nd outside the smller loop of the limçon r cos. r=4+3 sin r=sin 4 9 Sketch the curve nd find the re tht it encloses. 8. When recording live performnces, sound engineers often use microphone with crdioid pickup pttern becuse it suppresses noise from the udience. Suppose the microphone is plced 4 m from the front of the stge (s in the figure) nd the boundr of the optiml pickup region is 9. r 4 cos. r 3 cos stge. r cos 3. r cos m ; 3 4 Grph the curve nd find the re tht it encloses. 3. r sin 6 4. r sin 3 sin 9 udience 4 m microphone

6 SECTIN 9.5 CNIC SECTINS IN PLAR CRDINATES 59 given b the crdioid r 8 8 sin, where r is mesured in meters nd the microphone is t the pole. The musicins wnt to know the re the will hve on stge within the optiml pickup rnge of the microphone. Answer their question. 9 3 Find ll points of intersection of the given curves. 9. r cos, r cos 3. r cos 3, r sin 3 3. r sin, r sin 3. r sin, r cos Find the exct length of the polr curve. 33. r 3 sin, 34. r e, 35. r 36. r,, Use clcultor to find the length of the curve correct to four deciml plces. 37. r 3 sin 38. r 4 sin CNIC SECTINS IN PLAR CRDINATES In our previous stud of conic sections, prbols were defined in terms of focus nd directrix wheres ellipses nd hperbols were defined in terms of two foci. After reviewing those definitions nd equtions, we present more unified tretment of ll three tpes of conic sections in terms of focus nd directrix. Furthermore, if we plce the focus t the origin, then conic section hs simple polr eqution. In Chpter we will use the polr eqution of n ellipse to derive Kepler s lws of plnetr motion. CNICS IN CARTESIAN CRDINATES xis focus vertex FIGURE F prbol directrix Here we provide brief reminder of wht ou need to know bout conic sections. A more thorough review cn be found on the website Recll tht prbol is the set of points in plne tht re equidistnt from fixed point F (clled the focus) nd fixed line (clled the directrix). This definition is illustrted b Figure. Notice tht the point hlfw between the focus nd the directrix lies on the prbol; it is clled the vertex. The line through the focus perpendiculr to the directrix is clled the xis of the prbol. A prbol hs ver simple eqution if its vertex is plced t the origin nd its directrix is prllel to the x-xis or -xis. If the focus is on the -xis t the point, p, then the directrix hs the eqution p nd n eqution of the prbol is x 4p. [See prts () nd (b) of Figure.] If the focus is on the x-xis t p,, then the directrix is x p nd n eqution is 4px s in prts (c) nd (d). (, p) x =_p (, p) =_p x x=_p ( p, ) x ( p, ) x x=_p () =4p, p> (b) =4p, p< (c) =4px, p> (d) =4px, p< FIGURE