Section 15.3 Partial Derivatives
|
|
|
- Sybil Davis
- 6 years ago
- Views:
Transcription
1 Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a function f(x). In multivariable, this definition no longer makes sense because there are many different directions in which one could move, so the rate of change will depend not only upon the point we are at, but also the direction we choose to move. We illustrate with an example. Example.. A sheet of unevenly heated metal lies in the xy-plane with the lower left corner at the origin. The temperature at any point of the sheet is a function of x and y, T(x, y). After taking some measurements, you gather the following information: y/x If we are stood at the point (2, ) in the xy-plane, the temperature changes depending upon the direction we choose to mover. If we fix the y-value at and move in the positive x-direction, then the function becomes a function of a single variable, so we can consider its rate of change in the x-direction. Specifically, we have T T(3, ) T(2, ) (x, ) = = 25, so the rate of change of temperature in the x-direction is approximately 25 degrees per unit moved. This means that the temperature is increasing in the x-direction quite quickly. Likewise, in the y-direction we can consider the rate of change like with a single variable function. Specifically, fixing x = 2, we have T T(2, 2) T(2, ) (2, y) = = 5, so the rate of change is negative in the y-direction (meaning the temperature is dropping in the y-direction). In order to define derivatives for functions of more than one variable, we can generalize the ideas from this example. That is, we can consider rates of change of a function in the directions of the different coordinate
2 2 axis by keeping all other variables fixed and treating the function like a function of a single variable. We formalize the definition: Definition.2. Suppose f(x, y) is a function of two variables. Then we define its partial derivative to be the functions f x and f y defined by f(x + h, y) f(x, y) f x = lim h 0 h f(x, y + h) f(x, y) f y = lim h 0 h There are many different notations used to denote partial derivatives. Some of the more common are: f x (x, y) = f x = x = x f(x, y) = f = D f = D x f and likewise for y. Since the definition for partial derivatives is a direction generalization of regular single variable derivatives, calculation is almost identical. Specifically, we have: Result.3. To find the partial derivatives of f(x, y), we do the following: (i) To find f x, treat y like a constant and differentiate with respect to x. (ii) To find f y, treat x like a constant and differentiate with respect to y. Example.4. Let f(x, y) = sin (x) + y 2 xy. (i) Find the partial derivatives of f(x, y). This is straight forward - f x = cos (x) y and f y = 2y x. (ii) Find f x (0, 2). We know f x = cos (x) y, so f x (0, 2) = 2 = Interpreting Partial Derivatives As with single variable calculus, partial derivatives have a meaningful geometric interpretation. Specifically, the value of f x (a, b) is the slope of the function f(x, y) at the point (a, b) in the direction of the unit vector i. Likewise, f y (a, b) is the slope of the function f(x, y) at the point (a, b) in the direction of the unit vector j. Alternatively, we can think of f x (a, b) as the slope of the curve at the intersection of the graph of z = f(x, y) with the plane y = b at the point x = a (see illustration below). Likewise, we can think of f y (a, b) as the slope of the curve at the intersection of the graph of z = f(x, y) with the plane x = a at the point y = b.
3 3 Example 2.. Find the slopes of the function f(x, y) = x 2 +y 2 at the point (2, 3) in the y and x directions. f x = 2x, so f x (2, 3) = 4, and f y = 2y, so f y (2, 3) = 6. Example 2.2. If f(x, y) = sin (x) x 2 + y find x We have and y x = cos (x)(x2 + y) 2x sin (x) and (x 2 + y) 2 y = sin (x) (x 2 + y) 2 3. Functions of more than two variables Partial derivatives can be define for functions of lots of variables in exactly the same way as we defined them for functions of two variables. Specifically, if y = f(x,..., x n ) is a function in n variables, we define the partial derivative f xi to be the slope in the direction of the x i axis. It is calculated in exactly the same way as f x - we simply consider all other variables as constants and differentiate with respect to the relevant one. Example 3.. Find a formula for f xi for arbitrary i given that f(x,...,x n ) = x + + x n. Notice that this equation is linear in all directions with a slope of, so for any i we have f xi =.
4 4 4. Higher Derivatives Just as with single variable, we can differentiate a function many times. However, with multivariable functions, there are lots of different variables we can differentiate with respect to, so we need to be careful to give suitable notation so we know when calculating higher derivatives which variable to differentiate with respect to and when. Result 4.. Suppose f is a function of 2 variables x and y. We define the second partial derivatives of f as follows: (i) The second partial derivative with respect to x: f xx = (f x ) x = x x = 2 f x x (ii) The mixed partial derivative with respect to y and then x : f xy = (f x ) y = x y = 2 f x y (iii) The mixed partial derivative with respect to x and then y : f yx = (f y ) x = y x = 2 f y x We define the second partial derivatives with respect to y in a similar way, and in general we can define the kth partial derivative of a function f(x,...,x n ) with respect to different variables in a similar way. Calculation is straight forward. Example 4.2. Calculate f xx, f yy, f xy and f yx for the following: (i) f(x, y) = x 2 y 2 + xy f xx = 2y 2, f yy = 2x 2, f xy = 4xy + and f yx = 4xy + (ii) f(x, y) = y x + y2 f xx = 2y x 3,f yy = 2, f xy = x 2 and f yx = x 2 Notice that in both these cases, we have f xy = f yx. Though this is not always true, it is true provided we add certain additional conditions. Specifically, we have the following result: Result 4.3. (Clairauts Theorem) If the functions f xy and f yx are continuous, then f yx = f xy. We finish with an example of how to determine partial derivatives when looking at graphs.
5 Example 4.4. You are stood at the point (, ) on top of a hill. What are the signs of the following partial derivatives? x y 2 3 f x - negative - when you walk in the x-direction, you will move down f y - negative - when you walk in the y-direction, you will move down f xx - negative - contours are getting closer together, so the hill is getting steeper, so the graph is concave down f yy - negative - contours are getting closer together, so the hill is getting steeper, so the graph is concave down f xy - positive - f xy is te rate of change of f x as y increase. If we fix and and move in the positive y-direction, then the contours in the x- direction are getting closer together. Notice also that the values of f x are positive, so the positive values of f x are getting larger, as y increases, so f xy is positive.
Calculus II Fall 2014
 Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables
 Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Exam 2 Review Sheet. r(t) = x(t), y(t), z(t)
 Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
MATH 105: Midterm #1 Practice Problems
 Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Functions of several variables
 Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Level Curves, Partial Derivatives
 Unit #18 : Level Curves, Partial Derivatives Goals: To learn how to use and interpret contour diagrams as a way of visualizing functions of two variables. To study linear functions of two variables. To
Unit #18 : Level Curves, Partial Derivatives Goals: To learn how to use and interpret contour diagrams as a way of visualizing functions of two variables. To study linear functions of two variables. To
Unit 7 Partial Derivatives and Optimization
 Unit 7 Partial Derivatives and Optimization We have learned some important applications of the ordinary derivative in finding maxima and minima. We now move on to a topic called partial derivatives which
Unit 7 Partial Derivatives and Optimization We have learned some important applications of the ordinary derivative in finding maxima and minima. We now move on to a topic called partial derivatives which
Math 2411 Calc III Practice Exam 2
 Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
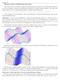 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
The Chain Rule, Higher Partial Derivatives & Opti- mization
 The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
CHAPTER 11 PARTIAL DERIVATIVES
 CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
MATH 12 CLASS 9 NOTES, OCT Contents 1. Tangent planes 1 2. Definition of differentiability 3 3. Differentials 4
 MATH 2 CLASS 9 NOTES, OCT 0 20 Contents. Tangent planes 2. Definition of differentiability 3 3. Differentials 4. Tangent planes Recall that the derivative of a single variable function can be interpreted
MATH 2 CLASS 9 NOTES, OCT 0 20 Contents. Tangent planes 2. Definition of differentiability 3 3. Differentials 4. Tangent planes Recall that the derivative of a single variable function can be interpreted
[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and
![[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and [f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and](/thumbs/92/108353356.jpg) Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
LECTURE 19 - LAGRANGE MULTIPLIERS
 LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
Math 5BI: Problem Set 1 Linearizing functions of several variables
 Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Differentiable functions (Sec. 14.4)
 Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Math 32, October 22 & 27: Maxima & Minima
 Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Test Yourself. 11. The angle in degrees between u and w. 12. A vector parallel to v, but of length 2.
 Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
ANSWER KEY. (a) For each of the following partials derivatives, use the contour plot to decide whether they are positive, negative, or zero.
 Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
11.2 LIMITS AND CONTINUITY
 11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
Review Sheet for Math 230, Midterm exam 2. Fall 2006
 Review Sheet for Math 230, Midterm exam 2. Fall 2006 October 31, 2006 The second midterm exam will take place: Monday, November 13, from 8:15 to 9:30 pm. It will cover chapter 15 and sections 16.1 16.4,
Review Sheet for Math 230, Midterm exam 2. Fall 2006 October 31, 2006 The second midterm exam will take place: Monday, November 13, from 8:15 to 9:30 pm. It will cover chapter 15 and sections 16.1 16.4,
14.4. Tangent Planes. Tangent Planes. Tangent Planes. Tangent Planes. Partial Derivatives. Tangent Planes and Linear Approximations
 14 Partial Derivatives 14.4 and Linear Approximations Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Suppose a surface S has equation z = f(x, y), where
14 Partial Derivatives 14.4 and Linear Approximations Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Suppose a surface S has equation z = f(x, y), where
i + u 2 j be the unit vector that has its initial point at (a, b) and points in the desired direction. It determines a line in the xy-plane:
 1 Directional Derivatives and Gradients Suppose we need to compute the rate of change of f(x, y) with respect to the distance from a point (a, b) in some direction. Let u = u 1 i + u 2 j be the unit vector
1 Directional Derivatives and Gradients Suppose we need to compute the rate of change of f(x, y) with respect to the distance from a point (a, b) in some direction. Let u = u 1 i + u 2 j be the unit vector
Maxima and Minima. Terminology note: Do not confuse the maximum f(a, b) (a number) with the point (a, b) where the maximum occurs.
 10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
Calculus 3 Exam 2 31 October 2017
 Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives
 ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives So far we have dealt with functions of the form y = f(x),
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives So far we have dealt with functions of the form y = f(x),
Lecture 4 : Monday April 6th
 Lecture 4 : Monday April 6th jacques@ucsd.edu Key concepts : Tangent hyperplane, Gradient, Directional derivative, Level curve Know how to find equation of tangent hyperplane, gradient, directional derivatives,
Lecture 4 : Monday April 6th jacques@ucsd.edu Key concepts : Tangent hyperplane, Gradient, Directional derivative, Level curve Know how to find equation of tangent hyperplane, gradient, directional derivatives,
Solutions to the problems from Written assignment 2 Math 222 Winter 2015
 Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
Review guide for midterm 2 in Math 233 March 30, 2009
 Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Partial Differentiation 1 Introduction
 Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Multivariate Calculus
 Multivariate Calculus Partial Derivatives 1 Theory Recall the definition of the partial derivatives of a function of two variables, z = f(x, y): f x = lim f(x + x, y) f(x, y) x 0 x f y f(x, y + y) f(x,
Multivariate Calculus Partial Derivatives 1 Theory Recall the definition of the partial derivatives of a function of two variables, z = f(x, y): f x = lim f(x + x, y) f(x, y) x 0 x f y f(x, y + y) f(x,
B) 0 C) 1 D) No limit. x2 + y2 4) A) 2 B) 0 C) 1 D) No limit. A) 1 B) 2 C) 0 D) No limit. 8xy 6) A) 1 B) 0 C) π D) -1
 MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
MATH 8 FALL 2010 CLASS 27, 11/19/ Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits
 MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
Chapter 9 Linear equations/graphing. 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane
 Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
18.3. Stationary Points. Introduction. Prerequisites. Learning Outcomes
 Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Review Problems. Calculus IIIA: page 1 of??
 Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
MATH 234 THIRD SEMESTER CALCULUS
 MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
REVIEW SHEET FOR MIDTERM 2: ADVANCED
 REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
MULTI-VARIABLE OPTIMIZATION NOTES. 1. Identifying Critical Points
 MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
Partial derivatives and their application.
 Math 2080 Week 10 Page 1 Gentry Publishing Chapter 10 Partial derivatives and their application. 10.1 Partial Derivatives 10.2 Tangent Planes and slopes of surfaces. 10.3 Linear approximations and the
Math 2080 Week 10 Page 1 Gentry Publishing Chapter 10 Partial derivatives and their application. 10.1 Partial Derivatives 10.2 Tangent Planes and slopes of surfaces. 10.3 Linear approximations and the
14.1 Functions of Several Variables
 14 Partial Derivatives 14.1 Functions of Several Variables Copyright Cengage Learning. All rights reserved. 1 Copyright Cengage Learning. All rights reserved. Functions of Several Variables In this section
14 Partial Derivatives 14.1 Functions of Several Variables Copyright Cengage Learning. All rights reserved. 1 Copyright Cengage Learning. All rights reserved. Functions of Several Variables In this section
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A
 Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
MATH 20C: FUNDAMENTALS OF CALCULUS II FINAL EXAM
 MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
MATH Review Exam II 03/06/11
 MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
Section 1.3. Slope formula: If the coordinates of two points on the line are known then we can use the slope formula to find the slope of the line.
 MATH 11009: Linear Functions Section 1.3 Linear Function: A linear function is a function that can be written in the form f(x) = ax + b or y = ax + b where a and b are constants. The graph of a linear
MATH 11009: Linear Functions Section 1.3 Linear Function: A linear function is a function that can be written in the form f(x) = ax + b or y = ax + b where a and b are constants. The graph of a linear
4.4 Equations of Parallel and Perpendicular
 www.ck12.org Chapter 4. Determining Linear Equations 4.4 Equations of Parallel and Perpendicular Lines Learning Objectives Determine whether lines are parallel or perpendicular. Write equations of perpendicular
www.ck12.org Chapter 4. Determining Linear Equations 4.4 Equations of Parallel and Perpendicular Lines Learning Objectives Determine whether lines are parallel or perpendicular. Write equations of perpendicular
y-intercept remains constant?
 1. The graph of a line that contains the points ( 1, 5) and (4, 5) is shown below. Which best represents this line if the slope is doubled and the y-intercept remains constant? F) G) H) J) 2. The graph
1. The graph of a line that contains the points ( 1, 5) and (4, 5) is shown below. Which best represents this line if the slope is doubled and the y-intercept remains constant? F) G) H) J) 2. The graph
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Math 233. Extrema of Functions of Two Variables Basics
 Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
The Picture Tells the Linear Story
 The Picture Tells the Linear Story Students investigate the relationship between constants and coefficients in a linear equation and the resulting slopes and y-intercepts on the graphs. This activity also
The Picture Tells the Linear Story Students investigate the relationship between constants and coefficients in a linear equation and the resulting slopes and y-intercepts on the graphs. This activity also
10.1 Curves defined by parametric equations
 Outline Section 1: Parametric Equations and Polar Coordinates 1.1 Curves defined by parametric equations 1.2 Calculus with Parametric Curves 1.3 Polar Coordinates 1.4 Areas and Lengths in Polar Coordinates
Outline Section 1: Parametric Equations and Polar Coordinates 1.1 Curves defined by parametric equations 1.2 Calculus with Parametric Curves 1.3 Polar Coordinates 1.4 Areas and Lengths in Polar Coordinates
4 to find the dimensions of the rectangle that have the maximum area. 2y A =?? f(x, y) = (2x)(2y) = 4xy
 Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
Section 3: Functions of several variables.
 Section 3: Functions of several variables. Compiled by Chris Tisdell S1: Motivation S2: Function of two variables S3: Visualising and sketching S4: Limits and continuity S5: Partial differentiation S6:
Section 3: Functions of several variables. Compiled by Chris Tisdell S1: Motivation S2: Function of two variables S3: Visualising and sketching S4: Limits and continuity S5: Partial differentiation S6:
Math Final Exam - 6/11/2015
 Math 200 - Final Exam - 6/11/2015 Name: Section: Section Class/Times Instructor Section Class/Times Instructor 1 9:00%AM ( 9:50%AM Papadopoulos,%Dimitrios 11 1:00%PM ( 1:50%PM Swartz,%Kenneth 2 11:00%AM
Math 200 - Final Exam - 6/11/2015 Name: Section: Section Class/Times Instructor Section Class/Times Instructor 1 9:00%AM ( 9:50%AM Papadopoulos,%Dimitrios 11 1:00%PM ( 1:50%PM Swartz,%Kenneth 2 11:00%AM
Math 206 First Midterm February 1, 2012
 Math 206 First Midterm February 1, 2012 Name: Instructor: Section: 1. Do not open this exam until you are told to do so. 2. This exam has 7 pages including this cover AND IS DOUBLE SIDED. There are 8 problems.
Math 206 First Midterm February 1, 2012 Name: Instructor: Section: 1. Do not open this exam until you are told to do so. 2. This exam has 7 pages including this cover AND IS DOUBLE SIDED. There are 8 problems.
Discussion 8 Solution Thursday, February 10th. Consider the function f(x, y) := y 2 x 2.
 Discussion 8 Solution Thursday, February 10th. 1. Consider the function f(x, y) := y 2 x 2. (a) This function is a mapping from R n to R m. Determine the values of n and m. The value of n is 2 corresponding
Discussion 8 Solution Thursday, February 10th. 1. Consider the function f(x, y) := y 2 x 2. (a) This function is a mapping from R n to R m. Determine the values of n and m. The value of n is 2 corresponding
MATH Exam 2 Solutions November 16, 2015
 MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
Exam 1 Study Guide. Math 223 Section 12 Fall Student s Name
 Exam 1 Study Guide Math 223 Section 12 Fall 2015 Dr. Gilbert Student s Name The following problems are designed to help you study for the first in-class exam. Problems may or may not be an accurate indicator
Exam 1 Study Guide Math 223 Section 12 Fall 2015 Dr. Gilbert Student s Name The following problems are designed to help you study for the first in-class exam. Problems may or may not be an accurate indicator
Directional Derivative, Gradient and Level Set
 Directional Derivative, Gradient and Level Set Liming Pang 1 Directional Derivative Te partial derivatives of a multi-variable function f(x, y), f f and, tell us te rate of cange of te function along te
Directional Derivative, Gradient and Level Set Liming Pang 1 Directional Derivative Te partial derivatives of a multi-variable function f(x, y), f f and, tell us te rate of cange of te function along te
Now we are going to introduce a new horizontal axis that we will call y, so that we have a 3-dimensional coordinate system (x, y, z).
 Example 1. A circular cone At the right is the graph of the function z = g(x) = 16 x (0 x ) Put a scale on the axes. Calculate g(2) and illustrate this on the diagram: g(2) = 8 Now we are going to introduce
Example 1. A circular cone At the right is the graph of the function z = g(x) = 16 x (0 x ) Put a scale on the axes. Calculate g(2) and illustrate this on the diagram: g(2) = 8 Now we are going to introduce
Determine the intercepts of the line and ellipse below: Definition: An intercept is a point of a graph on an axis. Line: x intercept(s)
 Topic 1 1 Intercepts and Lines Definition: An intercept is a point of a graph on an axis. For an equation Involving ordered pairs (x, y): x intercepts (a, 0) y intercepts (0, b) where a and b are real
Topic 1 1 Intercepts and Lines Definition: An intercept is a point of a graph on an axis. For an equation Involving ordered pairs (x, y): x intercepts (a, 0) y intercepts (0, b) where a and b are real
Plotting Points in 2-dimensions. Graphing 2 variable equations. Stuff About Lines
 Plotting Points in 2-dimensions Graphing 2 variable equations Stuff About Lines Plotting Points in 2-dimensions Plotting Points: 2-dimension Setup of the Cartesian Coordinate System: Draw 2 number lines:
Plotting Points in 2-dimensions Graphing 2 variable equations Stuff About Lines Plotting Points in 2-dimensions Plotting Points: 2-dimension Setup of the Cartesian Coordinate System: Draw 2 number lines:
Math 122: Final Exam Review Sheet
 Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
Chapter 16. Partial Derivatives
 Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Name: ID: Section: Math 233 Exam 2. Page 1. This exam has 17 questions:
 Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
Calculus I Handout: Curves and Surfaces in R 3. 1 Curves in R Curves in R 2 1 of 21
 1. Curves in R 2 1 of 21 Calculus I Handout: Curves and Surfaces in R 3 Up until now, everything we have worked with has been in two dimensions. But we can extend the concepts of calculus to three dimensions
1. Curves in R 2 1 of 21 Calculus I Handout: Curves and Surfaces in R 3 Up until now, everything we have worked with has been in two dimensions. But we can extend the concepts of calculus to three dimensions
DIFFERENTIAL EQUATIONS. A principal model of physical phenomena.
 DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The ordinary differential equation: The initial value: y = f(x, y) y(x 0 )=Y 0 Find a solution Y (x) onsomeintervalx 0 x b. Together these
DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The ordinary differential equation: The initial value: y = f(x, y) y(x 0 )=Y 0 Find a solution Y (x) onsomeintervalx 0 x b. Together these
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers
 SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
Section 5.2 Graphs of the Sine and Cosine Functions
 A Periodic Function and Its Period Section 5.2 Graphs of the Sine and Cosine Functions A nonconstant function f is said to be periodic if there is a number p > 0 such that f(x + p) = f(x) for all x in
A Periodic Function and Its Period Section 5.2 Graphs of the Sine and Cosine Functions A nonconstant function f is said to be periodic if there is a number p > 0 such that f(x + p) = f(x) for all x in
Calculus of Several Variables
 Benjamin McKay Calculus of Several Variables Optimisation and Finance February 18, 2018 This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. Preface The course is
Benjamin McKay Calculus of Several Variables Optimisation and Finance February 18, 2018 This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. Preface The course is
Limits and Continuity
 Limits and Continuity February 26, 205 Previously, you learned about the concept of the it of a function, and an associated concept, continuity. These concepts can be generalised to functions of several
Limits and Continuity February 26, 205 Previously, you learned about the concept of the it of a function, and an associated concept, continuity. These concepts can be generalised to functions of several
Lecture 19. Vector fields. Dan Nichols MATH 233, Spring 2018 University of Massachusetts. April 10, 2018.
 Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Examples: Find the domain and range of the function f(x, y) = 1 x y 2.
 Multivariate Functions In this chapter, we will return to scalar functions; thus the functions that we consider will output points in space as opposed to vectors. However, in contrast to the majority of
Multivariate Functions In this chapter, we will return to scalar functions; thus the functions that we consider will output points in space as opposed to vectors. However, in contrast to the majority of
14.2 Limits and Continuity
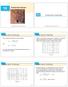 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
4 The Cartesian Coordinate System- Pictures of Equations
 The Cartesian Coordinate System- Pictures of Equations Concepts: The Cartesian Coordinate System Graphs of Equations in Two Variables x-intercepts and y-intercepts Distance in Two Dimensions and the Pythagorean
The Cartesian Coordinate System- Pictures of Equations Concepts: The Cartesian Coordinate System Graphs of Equations in Two Variables x-intercepts and y-intercepts Distance in Two Dimensions and the Pythagorean
33. Riemann Summation over Rectangular Regions
 . iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
. iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
Review #Final Exam MATH 142-Drost
 Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
LEIBNIZ INDIFFERENCE CURVES AND THE MARGINAL RATE OF SUBSTITUTION
 3.2.1 INDIFFERENCE CURVES AND THE MARGINAL RATE OF SUBSTITUTION Alexei cares about his exam grade and his free time. We have seen that his preferences can be represented graphically using indifference
3.2.1 INDIFFERENCE CURVES AND THE MARGINAL RATE OF SUBSTITUTION Alexei cares about his exam grade and his free time. We have seen that his preferences can be represented graphically using indifference
MATH 261 EXAM II PRACTICE PROBLEMS
 MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
WESI 205 Workbook. 1 Review. 2 Graphing in 3D
 1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
11/1/2017 Second Hourly Practice 2 Math 21a, Fall Name:
 11/1/217 Second Hourly Practice 2 Math 21a, Fall 217 Name: MWF 9 Jameel Al-Aidroos MWF 9 Dennis Tseng MWF 1 Yu-Wei Fan MWF 1 Koji Shimizu MWF 11 Oliver Knill MWF 11 Chenglong Yu MWF 12 Stepan Paul TTH
11/1/217 Second Hourly Practice 2 Math 21a, Fall 217 Name: MWF 9 Jameel Al-Aidroos MWF 9 Dennis Tseng MWF 1 Yu-Wei Fan MWF 1 Koji Shimizu MWF 11 Oliver Knill MWF 11 Chenglong Yu MWF 12 Stepan Paul TTH
Review for Mastery. Identifying Linear Functions
 Identifying Linear Functions You can determine if a function is linear by its graph, ordered pairs, or equation. Identify whether the graph represents a linear function. Step 1: Determine whether the graph
Identifying Linear Functions You can determine if a function is linear by its graph, ordered pairs, or equation. Identify whether the graph represents a linear function. Step 1: Determine whether the graph
Lecture 15. Global extrema and Lagrange multipliers. Dan Nichols MATH 233, Spring 2018 University of Massachusetts
 Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Section 7.2 Logarithmic Functions
 Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
DIFFERENTIAL EQUATIONS. A principal model of physical phenomena.
 DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The equation: The initial value: y = f(x, y) y(x 0 ) = Y 0 Find solution Y (x) on some interval x 0 x b. Together these two conditions constitute
DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The equation: The initial value: y = f(x, y) y(x 0 ) = Y 0 Find solution Y (x) on some interval x 0 x b. Together these two conditions constitute
1. Let f(x, y) = 4x 2 4xy + 4y 2, and suppose x = cos t and y = sin t. Find df dt using the chain rule.
 Math 234 WES WORKSHEET 9 Spring 2015 1. Let f(x, y) = 4x 2 4xy + 4y 2, and suppose x = cos t and y = sin t. Find df dt using the chain rule. 2. Let f(x, y) = x 2 + y 2. Find all the points on the level
Math 234 WES WORKSHEET 9 Spring 2015 1. Let f(x, y) = 4x 2 4xy + 4y 2, and suppose x = cos t and y = sin t. Find df dt using the chain rule. 2. Let f(x, y) = x 2 + y 2. Find all the points on the level
Level Curves in Matlab
 College of the Redwoods Mathematics Department Multivariable Calculus Level Curves in Matlab David Arnold Directory Table of Contents. Begin Article. Copyright c 999 darnold@northcoast.com Last Revision
College of the Redwoods Mathematics Department Multivariable Calculus Level Curves in Matlab David Arnold Directory Table of Contents. Begin Article. Copyright c 999 darnold@northcoast.com Last Revision
6.1 - Introduction to Periodic Functions
 6.1 - Introduction to Periodic Functions Periodic Functions: Period, Midline, and Amplitude In general: A function f is periodic if its values repeat at regular intervals. Graphically, this means that
6.1 - Introduction to Periodic Functions Periodic Functions: Period, Midline, and Amplitude In general: A function f is periodic if its values repeat at regular intervals. Graphically, this means that
Study Guide and Review - Chapter 3. Find the x-intercept and y-intercept of the graph of each linear function.
 Find the x-intercept and y-intercept of the graph of each linear function. 11. The x-intercept is the point at which the y-coordinate is 0, or the line crosses the x-axis. So, the x-intercept is 8. The
Find the x-intercept and y-intercept of the graph of each linear function. 11. The x-intercept is the point at which the y-coordinate is 0, or the line crosses the x-axis. So, the x-intercept is 8. The
Mathematics 205 HWK 2 Solutions Section 12.4 p588. x\y 0 1 2
 Mathematics 205 HWK 2 Solutions Section 12.4 p588 Problem 3, 12.4, p588. Decide whether the table of values could represent values f a linear function. x\y 0 1 2 0 0 5 10 1 2 7 12 2 4 9 14 Solution. F
Mathematics 205 HWK 2 Solutions Section 12.4 p588 Problem 3, 12.4, p588. Decide whether the table of values could represent values f a linear function. x\y 0 1 2 0 0 5 10 1 2 7 12 2 4 9 14 Solution. F
LEVEL 9 Mathematics Observation
 LEVEL 9 Mathematics Observation Student: Assessment Date: Grade in School: Concepts Evaluated Score Notes. Applying the concept of slope to determine rate of change Equation of a line: slope-intercept
LEVEL 9 Mathematics Observation Student: Assessment Date: Grade in School: Concepts Evaluated Score Notes. Applying the concept of slope to determine rate of change Equation of a line: slope-intercept
Math 259 Winter Recitation Handout 9: Lagrange Multipliers
 Math 259 Winter 2009 Recitation Handout 9: Lagrange Multipliers The method of Lagrange Multipliers is an excellent technique for finding the global maximum and global minimum values of a function f(x,
Math 259 Winter 2009 Recitation Handout 9: Lagrange Multipliers The method of Lagrange Multipliers is an excellent technique for finding the global maximum and global minimum values of a function f(x,
