(1) Primary Trigonometric Ratios (SOH CAH TOA): Given a right triangle OPQ with acute angle, we have the following trig ratios: ADJ
|
|
|
- Eleanore Stephens
- 6 years ago
- Views:
Transcription
1 Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When sked to solve tringle, we must determine the mesure of ll of its ngles nd side lengths. In our ttempt to find these vlues, we re likely to onsider one or more of the following formuls. (1) Primry Trigonometri Rtios (SOH CAH TOA): Given right tringle OPQ with ute ngle, we hve the following trig rtios: sin = OPP HYP, ADJ os = nd tn = OPP HYP ADJ Here, HYP denotes the hypotenuse, whih is lwys ross from the right ngle. OPP denotes the side opposite/ross from the ngle ADJ denotes the side djent/eside the ngle, tht is not HYP. Applile to: right tringles only. To egin solving tringle, we need two known onstrints (e.g. two sides or one side nd n ute ngle) (2) Lw of Sines Given ny tringle ABC, we hve the following: sin A = sin B = sin C () sin A = sin B = sin C Applile to: ny tringle. To egin solving tringle, we need three known onstrints. Two of the three onstrints must inlude n ngle nd the side length ross from it. Mking Mth Possile 1 of 11 S diyy Hendrikson
2 Tringles nd Trigonometry Level: x 2 + y 2 =1 (3) Lw of Cosines Given ny tringle ABC, we hve the following: 2 = os C () 2 = os B () 2 = os A Applile to: ny tringle. To egin solving tringle, we need three known onstrints tht inlude either ll three side lengths or two side lengths nd the ngle in etween. Why re the ove formuls helpful when solving tringle? Answer: These formuls help us to relte the ngles of the tringle to its side lengths! (1) Primry Trig Rtios re only vlid when solving right tringles. (2) The Lws of Sines nd Cosines re vlid for ny tringle, so long s there is enough given informtion to sustitute into the formuls. (3) Although the Lws of Sines nd Cosines re pplile to right tringles, it is est prtie nd most e ient to use the Primry Trig Rtios. Below, we will explore these formuls nd pply them in some worked exmples! Given right tringle OPQ with ute ngle, we hve the following trig rtios: sin = OPP HYP, ADJ os = HYP nd tn = OPP ADJ Justifition: Notie tht the tringle in the unit irle hs the following side lengths: sin (height), os (se) nd 1 (sine the hypotenuse is rdius of the unit irle). Furthermore, this tringle is similr to 4OPQ y AAA similrity. Thus, y definition of similrity, we hve: sin 1 = OPP HYP nd os 1 = ADJ HYP ) tn = sin os = OPP HYP ADJ HYP = OPP ADJ Mking Mth Possile 2 of 11 S diyy Hendrikson
3 Tringles nd Trigonometry Level: x 2 + y 2 =1 Exerise 1: Solve the following tringles. Given ny tringle ABC, we hve the following: sin A = sin B = sin C () sin A = sin B = sin C Proof: Consider ny tringle ABC, oriented so tht the se is AC = (s shown) nd the ltitude, of length h, extends from the vertex t B. By our primry trig rtios, we know tht sin A = OPP HYP = h. Rerrnging, we hve tht h = sin A. It then follows tht the re of this tringle n e expressed s follows: Are = 1 2 se height = 1 2 sin A. We n lso orient the tringle so tht its se is AB = or BC =. From these orienttions, we find tht Are = 1 2 se height = 1 2 sin B or 1 2 sin C, respetively. In summry, we ve found tht: Are = 1 2 sin A = 1 2 sin B = 1 2 sin C Multiplying this eqution through y sin A = gives: = 1 2 sin B This is the required result, whih onludes the proof sin C ) sin A = sin B = sin C Mking Mth Possile 3 of 11 S diyy Hendrikson
4 Exploring Sine Lw Level: x 2 + y 2 =1 Consider the tringle ABC, s shown. In the digrm, \A is ross from side length, \B is ross from side length nd \C is ross from side length. This is onventionl nottion. We will ll the ngle nd the side length ross from it n opposites omo. The equtions quired from the Lw of Sines re s follows: sin A = sin B, sin A = sin C nd sin B = sin C Notie tht the ove equtions would only e helpful while solving tringle if we hve t lest three piees of informtion, whih n rise in one of the following wys: (1) Two ngles nd one side (resulting in n opposites omo nd n dditionl ngle), or (2) An opposites omo nd n dditionl side (resulting in two known sides). Notie tht if we re ever given tringle with two ngles, 1 nd 2, we n determine the third ngle y simply lulting the vlue of 3 = 180 ( ). Thus, ny side length tht is given will give us n opposites omo with one of the known ngles! For exmple, suppose we re given. Then, the opposites omo will inlude \B, whih we will lso know. Also, the given side length is n dditionl onstrint tht helps to produe unique tringle. Exerise 2: Solve the tringle elow, suh tht = 5, \A = 62 nd \C = 54. Mking Mth Possile 4 of 11 S diyy Hendrikson
5 Exploring Lw of Sines Level: x 2 + y 2 =1 Suppose we re given n ritrry tringle with onstrints onsisting of the following: two side lengths nd n ngle tht is ross from one of the given sides Question: Will these ontrints lwys produe unique tringle? Answer: Unfortuntely not. Any tringle with the onstrints desried ove will fll into one of the tegories given elow. The side ross from the given ngle will hve length tht is: (1) equl to the other known side length (2) shorter thn the other known side length (3) longer thn the other known side length In the se of (1), we hve n isoseles tringle, whih unovers n dditionl ngle. Therefore, we will hve unique tringle with ll known ngles nd one missing side, whih n e found esily. Figures 1-4 elow explore ll possile outomes tht fll under ses (2) nd (3). When onstruting digrm, note tht n opposites omo plus n dditionl side does not tell us nything out the ngle etween the sides whose lengths re given. In the figures elow, this would e \B. Tht mens tht when skething tringle with the given onditions, our sketh will e tenttive, sine it hnges when we vry the size of \B. These vritions re shown in the digrms. Some hoies of \B produe tringle tht stisfies the given onditions, while others do not! Figure 1 Figure 2 Figure 3 Figure 4 Figures 1, 2 nd 3 fll under se (2), while Figure 4 flls under se (3). Cse 1 Amiguous Cse ) Side ross from given ngle is shorter thn other known side Under this se, we hve three possile outomes. () No tringle exists with the given onstrints. (See Figure 1) This is euse the side length ross from the given ngle is too short! () Two tringles stisfy the given onstrints. (See Figure 2) () A right tringle stisfies the given onstrints. (See Figure 3) Mking Mth Possile 5 of 11 S diyy Hendrikson
6 Exploring Lw of Sines Level: x 2 + y 2 =1 Question: Cn we identify whih outome will our efore tully solving n exerise? Answer: Yes! However, given tht we must solve the tringle either wy, some folks prefer to dive into the exerise, wre tht ny of the three outomes my rise. If you re urious nd would like to know how determine the outome prior to solving, see the explntion elow. On the other hnd, if you would like to egin solving tringles nd disovering outomes s you go, see the Worked Exmples setion elow! Explntion Consider the following tringle, whih we sw during the proof for the Lw of Sines. Now, suppose tht we re sked to solve tringle with known vlues for \A nd side lengths nd, s seen in Figures 1-4. Rell tht our primry trig rtios gve tht the length of the ltitude is h = sin A, vlue tht we d e le to lulte using the given informtion. How does knowing the height of the tringle help us? Let s revisit Figures 1-3, elow. Eh figure hs distint reltionship with the height of the tringle. () No Solution (Figure 1): The height, h, isgreter thn the side ross from the given ngle. () Two Solutions (Figure 2): The height, h, isless thn the side ross from the given ngle. () A right tringle (Figure 3): The height, h, isequl to the side ross from the given ngle. If you find the ove results helpful, you re enourged to use them in the exerises tht follow! Exerise 3: Solve tringle ABC, with \B = 30, = 4 nd = 8. Mking Mth Possile 6 of 11 S diyy Hendrikson
7 Exploring Lw of Sines Level: x 2 + y 2 =1 Exerise 4: Solve tringle ABC, with \A = 31, = 62 nd = 130. Exerise 5: Solve tringle ABC, with \C = 27, = 12 nd = 24. Mking Mth Possile 7 of 11 S diyy Hendrikson
8 Exploring Lw of Sines Level: x 2 + y 2 =1 Cse 2 Unique Tringle ) Side ross from given ngle is longer thn other known side Rell Figure 4, shown elow. Here, the given onstrints determine unique tringle! Exerise 6: Solve tringle ABC, with \A = 61, = 5 nd = 2. Mking Mth Possile 8 of 11 S diyy Hendrikson
9 Exploring Lw of Cosines Level: x 2 + y 2 =1 Given ny tringle ABC, we hve the following: 2 = os C () 2 = os B () 2 = os A Proof: Consider 4ABC oriented in the oordinte plne, suh tht its se is AB =. Notie tht we n lwys onstrut the unit irle suh tht 4AED is similr to 4AF C. We know tht DE = sin A =sina (in Qudrnt II) nd AE = os A, dueto the onstrution in the unit irle. Thus, y the definition of similrity, we hve the following: CF = DE () CF = DE = sin A, nd 1 EF = AE () EF = AE = os A 1 We now hve the se nd height of 4AF C. Thus, the oordintes of C re ( os A, sin A). Note tht these oordintes would hve een the sme if \A ws right or ute. (Cn you verify this?) Next, we onsider the side length BC =. Applying the distne formul to the points B (, 0) nd C ( os A, sin A), we hve the following result: 2 =( os A) 2 +(0 sin A) 2 = 2 2 os A + 2 os 2 A + 2 sin 2 A = 2 2 os A + 2 (os 2 A +sin 2 A) = 2 2 os A + 2 (1) sine os 2 A +sin 2 A =1 = os A The result ove proves the third formul in the sttement of the lw. To quire the remining two, we simply orient the tringle in the oordinte plne suh tht the se is BC = or AC =, nd proeed with the sme resoning s ove. The Lw of Cosines is helpful when we re given three onstrints without n opposites omo. There re extly two instnes in whih this ours: (1) Given onstrints: three side lengths (2) Given onstrints: the lengths of two sides nd the ngle in etween Unlike with the Lw of Sines, these onstrints will lwys produe unique tringle! Next, we will ttempt some worked exmples! Mking Mth Possile 9 of 11 S diyy Hendrikson
10 Exploring Lw of Cosines Level: x 2 + y 2 =1 Exerise 7: Use the Lw of Cosines to determine the indited side, x. Exerise 8: Use the Lw of Cosines to determine the indited ngle,. Mking Mth Possile 10 of 11 S diyy Hendrikson
11 Bringing Things Together Level: x 2 + y 2 =1 Exerise 9: In the digrm elow, AB = 6, BD = 4, \ABD = 45 nd \CBD = 30. Determine the side length BC, indited y x. Mking Mth Possile 11 of 11 S diyy Hendrikson
Section 6.1 Law of Sines. Notes. Oblique Triangles - triangles that have no right angles. A c. A is acute. A is obtuse
 Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
SOLVING TRIANGLES USING THE SINE AND COSINE RULES
 Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Notes on Spherical Triangles
 Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
REVIEW, pages
 REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
Pearson Education Limited Edinburgh Gate Harlow Essex CM20 2JE England and Associated Companies throughout the world
 Person Edution Limited Edinurgh Gte Hrlow Essex M20 2JE Englnd nd ssoited ompnies throughout the world Visit us on the World Wide We t: www.personed.o.uk Person Edution Limited 2014 ll rights reserved.
Person Edution Limited Edinurgh Gte Hrlow Essex M20 2JE Englnd nd ssoited ompnies throughout the world Visit us on the World Wide We t: www.personed.o.uk Person Edution Limited 2014 ll rights reserved.
REVIEW QUESTIONS TOPIC 5 TRIGONOMETRY I FLUENCY
 TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
8.1. The Sine Law. Investigate. Tools
 8.1 Te Sine Lw Mimi 50 ermud Tringle ermud 1600 km Sn Jun 74 Puerto Rio Te ermud Tringle, in te nort tlnti Oen, is te lotion of severl unexplined plne nd sip disppernes. Vrious teories ve een suggested
8.1 Te Sine Lw Mimi 50 ermud Tringle ermud 1600 km Sn Jun 74 Puerto Rio Te ermud Tringle, in te nort tlnti Oen, is te lotion of severl unexplined plne nd sip disppernes. Vrious teories ve een suggested
Patterns and Algebra
 Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS
 CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
Chapter 2: Pythagoras Theorem and Trigonometry (Revision)
 Chapter 2: Pythagoras Theorem and Trigonometry (Revision) Paper 1 & 2B 2A 3.1.3 Triangles Understand a proof of Pythagoras Theorem. Understand the converse of Pythagoras Theorem. Use Pythagoras 3.1.3 Triangles
Chapter 2: Pythagoras Theorem and Trigonometry (Revision) Paper 1 & 2B 2A 3.1.3 Triangles Understand a proof of Pythagoras Theorem. Understand the converse of Pythagoras Theorem. Use Pythagoras 3.1.3 Triangles
Lecture 16. Double integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Double Integrals over Rectangles
 Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of
Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of
c The scaffold pole EL is 8 m long. How far does it extend beyond the line JK?
 3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
Spherical Geometry. This is an article from my home page:
 Spheril Geometry This is n rtile from my home pge: www.olewitthnsen.dk Ole Witt-Hnsen nov. 6 Contents. Geometry on sphere.... Spheril tringles...3. Polr tringles...4 3. The right-ngle spheril tringle...6
Spheril Geometry This is n rtile from my home pge: www.olewitthnsen.dk Ole Witt-Hnsen nov. 6 Contents. Geometry on sphere.... Spheril tringles...3. Polr tringles...4 3. The right-ngle spheril tringle...6
Fubini for continuous functions over intervals
 Fuini for ontinuous funtions over intervls We first prove the following theorem for ontinuous funtions. Theorem. Let f(x) e ontinuous on ompt intervl =[, [,. Then [, [, [ [ f(x, y)(x, y) = f(x, y)y x =
Fuini for ontinuous funtions over intervls We first prove the following theorem for ontinuous funtions. Theorem. Let f(x) e ontinuous on ompt intervl =[, [,. Then [, [, [ [ f(x, y)(x, y) = f(x, y)y x =
Macroscopic and Microscopic Springs Procedure
 Mrosopi nd Mirosopi Springs Proedure OBJECTIVE Purpose In this l you will: investigte the spring-like properties of stright wire, disover the strethiness of mteril, independent of the size nd shpe of n
Mrosopi nd Mirosopi Springs Proedure OBJECTIVE Purpose In this l you will: investigte the spring-like properties of stright wire, disover the strethiness of mteril, independent of the size nd shpe of n
Math Circles Finite Automata Question Sheet 3 (Solutions)
 Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Using Trigonometric Ratios Part 1: Solving For Unknown Sides
 MPM2D: Principles of Mathematics Using Trigonometric Ratios Part 1: Solving For Unknown Sides J. Garvin Slide 1/15 Recap State the three primary trigonometric ratios for A in ABC. Slide 2/15 Recap State
MPM2D: Principles of Mathematics Using Trigonometric Ratios Part 1: Solving For Unknown Sides J. Garvin Slide 1/15 Recap State the three primary trigonometric ratios for A in ABC. Slide 2/15 Recap State
Triangles and parallelograms of equal area in an ellipse
 1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
Geometric quantities for polar curves
 Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Polar Coordinates. July 30, 2014
 Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY
 LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
Resistors, Current and Voltage measurements, Ohm s law, Kirchhoff s first and second law. Kirchhoff s first Objectives:
 EE -050 Ciruit L Experiment # esistors, Current nd Voltge mesurements, Ohm s lw, Kirhhoff s first nd seond lw. Kirhhoff s first Ojetives: Slmn in Adul Aziz University Eletril Engineering Deprtment. Fmiliriztion
EE -050 Ciruit L Experiment # esistors, Current nd Voltge mesurements, Ohm s lw, Kirhhoff s first nd seond lw. Kirhhoff s first Ojetives: Slmn in Adul Aziz University Eletril Engineering Deprtment. Fmiliriztion
First Round Solutions Grades 4, 5, and 6
 First Round Solutions Grdes 4, 5, nd 1) There re four bsic rectngles not mde up of smller ones There re three more rectngles mde up of two smller ones ech, two rectngles mde up of three smller ones ech,
First Round Solutions Grdes 4, 5, nd 1) There re four bsic rectngles not mde up of smller ones There re three more rectngles mde up of two smller ones ech, two rectngles mde up of three smller ones ech,
7KH4XLQFXQ; Earth/matriX SCIENCE IN ANCIENT ARTWORK. Charles William Johnson
 Erth/mtriX SCIENCE IN ANCIENT ARTWORK 7KH4XLQFXQ; Chrles Willim Johnson Erth/mtriX P.O. Box 231126, New Orlens, Louisin, 70183-1126 2001 Copyrighted y Chrles Willim Johnson www.erthmtrix.om www.the-periodi-tle.om
Erth/mtriX SCIENCE IN ANCIENT ARTWORK 7KH4XLQFXQ; Chrles Willim Johnson Erth/mtriX P.O. Box 231126, New Orlens, Louisin, 70183-1126 2001 Copyrighted y Chrles Willim Johnson www.erthmtrix.om www.the-periodi-tle.om
Theme: Don t get mad. Learn mod.
 FERURY When 1 is divided by 5, the reminder is. nother wy to sy this is opyright 015 The Ntionl ouncil of Techers of Mthemtics, Inc. www.nctm.org. ll rights reserved. This mteril my not be copied or distributed
FERURY When 1 is divided by 5, the reminder is. nother wy to sy this is opyright 015 The Ntionl ouncil of Techers of Mthemtics, Inc. www.nctm.org. ll rights reserved. This mteril my not be copied or distributed
Samantha s Strategies page 1 of 2
 Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Student Book SERIES. Patterns and Algebra. Name
 E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
10.4 AREAS AND LENGTHS IN POLAR COORDINATES
 65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
CS 135: Computer Architecture I. Boolean Algebra. Basic Logic Gates
 Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Section 16.3 Double Integrals over General Regions
 Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
SAMPLE. End of term: TEST A. Year 4. Name Class Date. Complete the missing numbers in the sequences below.
 End of term: TEST A You will need penil nd ruler. Yer Nme Clss Dte 2 Complete the missing numers in the sequenes elow. 50 25 00 75 8 30 3 28 2 9 Put irle round two of the shpes elow whih hve 3 shded. 3
End of term: TEST A You will need penil nd ruler. Yer Nme Clss Dte 2 Complete the missing numers in the sequenes elow. 50 25 00 75 8 30 3 28 2 9 Put irle round two of the shpes elow whih hve 3 shded. 3
TRIGONOMETRIC APPLICATIONS
 HPTER TRIGONOMETRI PPLITIONS n ocen is vst expnse tt cn e life-tretening to person wo experiences disster wile oting. In order for elp to rrive on time, it is necessry tt te cost gurd or sip in te re e
HPTER TRIGONOMETRI PPLITIONS n ocen is vst expnse tt cn e life-tretening to person wo experiences disster wile oting. In order for elp to rrive on time, it is necessry tt te cost gurd or sip in te re e
Defining the Rational Numbers
 MATH10 College Mthemtis - Slide Set 2 1. Rtionl Numers 1. Define the rtionl numers. 2. Redue rtionl numers.. Convert etween mixed numers nd improper frtions. 4. Express rtionl numers s deimls.. Express
MATH10 College Mthemtis - Slide Set 2 1. Rtionl Numers 1. Define the rtionl numers. 2. Redue rtionl numers.. Convert etween mixed numers nd improper frtions. 4. Express rtionl numers s deimls.. Express
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN. Inventor: Brian L. Baskin
 METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
The reciprocal identities are obvious from the definitions of the six trigonometric functions.
 The Fundamental Identities: (1) The reciprocal identities: csc = 1 sec = 1 (2) The tangent and cotangent identities: tan = cot = cot = 1 tan (3) The Pythagorean identities: sin 2 + cos 2 =1 1+ tan 2 =
The Fundamental Identities: (1) The reciprocal identities: csc = 1 sec = 1 (2) The tangent and cotangent identities: tan = cot = cot = 1 tan (3) The Pythagorean identities: sin 2 + cos 2 =1 1+ tan 2 =
EE Controls Lab #2: Implementing State-Transition Logic on a PLC
 Objective: EE 44 - Controls Lb #2: Implementing Stte-rnsition Logic on PLC ssuming tht speed is not of essence, PLC's cn be used to implement stte trnsition logic. he dvntge of using PLC over using hrdwre
Objective: EE 44 - Controls Lb #2: Implementing Stte-rnsition Logic on PLC ssuming tht speed is not of essence, PLC's cn be used to implement stte trnsition logic. he dvntge of using PLC over using hrdwre
How to work out trig functions of angles without a scientific calculator
 Before starting, you will need to understand how to use SOH CAH TOA. How to work out trig functions of angles without a scientific calculator Task 1 sine and cosine Work out sin 23 and cos 23 by constructing
Before starting, you will need to understand how to use SOH CAH TOA. How to work out trig functions of angles without a scientific calculator Task 1 sine and cosine Work out sin 23 and cos 23 by constructing
Probability and Statistics P(A) Mathletics Instant Workbooks. Copyright
 Proility nd Sttistis Student Book - Series K- P(A) Mthletis Instnt Workooks Copyright Student Book - Series K Contents Topis Topi - Review of simple proility Topi - Tree digrms Topi - Proility trees Topi
Proility nd Sttistis Student Book - Series K- P(A) Mthletis Instnt Workooks Copyright Student Book - Series K Contents Topis Topi - Review of simple proility Topi - Tree digrms Topi - Proility trees Topi
Lecture 20. Intro to line integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
EBU KNOCKOUT COMPETITIONS
 EBU KNOCKOUT COMPETITIONS GENERAL REGULATIONS 1 INTRODUCTION Vrious regultions pply to ll English Bridge Union ompetitions tht involve mthes plyed privtely. These ompetitions omprise: The knokout stges
EBU KNOCKOUT COMPETITIONS GENERAL REGULATIONS 1 INTRODUCTION Vrious regultions pply to ll English Bridge Union ompetitions tht involve mthes plyed privtely. These ompetitions omprise: The knokout stges
Kirchhoff s Rules. Kirchhoff s Laws. Kirchhoff s Rules. Kirchhoff s Laws. Practice. Understanding SPH4UW. Kirchhoff s Voltage Rule (KVR):
 SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
Example. Check that the Jacobian of the transformation to spherical coordinates is
 lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
Skills Practice Skills Practice for Lesson 4.1
 Skills Prctice Skills Prctice for Lesson.1 Nme Dte Tiling Bthroom Wll Simplifying Squre Root Expressions Vocbulry Mtch ech definition to its corresponding term. 1. n expression tht involves root. rdicnd
Skills Prctice Skills Prctice for Lesson.1 Nme Dte Tiling Bthroom Wll Simplifying Squre Root Expressions Vocbulry Mtch ech definition to its corresponding term. 1. n expression tht involves root. rdicnd
SLOVAK UNIVERSITY OF TECHNOLOGY Faculty of Material Science and Technology in Trnava. ELECTRICAL ENGINEERING AND ELECTRONICS Laboratory exercises
 SLOVAK UNIVERSITY OF TECHNOLOGY Fulty of Mteril Siene nd Tehnology in Trnv ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory exerises Róbert Riedlmjer TRNAVA 00 ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory
SLOVAK UNIVERSITY OF TECHNOLOGY Fulty of Mteril Siene nd Tehnology in Trnv ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory exerises Róbert Riedlmjer TRNAVA 00 ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory
+ sin bsin. sin. tan
 6. Spheril rignmetri Frmule Just s in plne gemetry, there re useful trignmetri frmule whih relte the sides nd vertex ngles f spheril tringles: Csine Frmul [6.1] s ss + sin sin s Sine Frmul [6.] sin sin
6. Spheril rignmetri Frmule Just s in plne gemetry, there re useful trignmetri frmule whih relte the sides nd vertex ngles f spheril tringles: Csine Frmul [6.1] s ss + sin sin s Sine Frmul [6.] sin sin
& Y Connected resistors, Light emitting diode.
 & Y Connected resistors, Light emitting diode. Experiment # 02 Ojectives: To get some hndson experience with the physicl instruments. To investigte the equivlent resistors, nd Y connected resistors, nd
& Y Connected resistors, Light emitting diode. Experiment # 02 Ojectives: To get some hndson experience with the physicl instruments. To investigte the equivlent resistors, nd Y connected resistors, nd
3/8" Square Multi-Turn Cermet Trimmer
 Vishy Sfernie 3/8" Squre Multi-Turn Cermet Trimmer FEATURES Industril grde W t 70 C The T93 is smll size trimmer - 3/8" x 3/8" x 3/16" - nswering PC ord mounting requirements. Five versions re ville whih
Vishy Sfernie 3/8" Squre Multi-Turn Cermet Trimmer FEATURES Industril grde W t 70 C The T93 is smll size trimmer - 3/8" x 3/8" x 3/16" - nswering PC ord mounting requirements. Five versions re ville whih
1 tray of toffee 1 bar of toffee. 10 In the decimal number, 0 7, the 7 refers to 7 tenths or
 Chpter 3 Deciml Numers Do you know wht DECIMAL is? In chpter, we delt with units, s, 0 s nd 00 s. When you tke single unit nd divide it into (or 0 or 00) its, wht we then hve re deciml frctions of whole
Chpter 3 Deciml Numers Do you know wht DECIMAL is? In chpter, we delt with units, s, 0 s nd 00 s. When you tke single unit nd divide it into (or 0 or 00) its, wht we then hve re deciml frctions of whole
Domination and Independence on Square Chessboard
 Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Yellowknife km Vancouver km NEL
 ic tio n Yellowknife Pr e- Pu bl 1566 km 67.3 Vncouver 112 1870 km hpter 3 tio n cute Tringle Trigonometry ic LERNING GOLS You will be ble to develop your sptil sense by Pr e- Pu bl? Using the sine lw
ic tio n Yellowknife Pr e- Pu bl 1566 km 67.3 Vncouver 112 1870 km hpter 3 tio n cute Tringle Trigonometry ic LERNING GOLS You will be ble to develop your sptil sense by Pr e- Pu bl? Using the sine lw
Polar coordinates 5C. 1 a. a 4. π = 0 (0) is a circle centre, 0. and radius. The area of the semicircle is π =. π a
 Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
Multivariable integration. Multivariable integration. Iterated integration
 Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Seven Sisters. Visit for video tutorials
 Seven Sisters This imge is from www.quiltstudy.org. Plese visit this website for more informtion on Seven Sisters quilt ptterns. Visit www.blocloc.com for video tutorils 1 The Seven Sisters design cn be
Seven Sisters This imge is from www.quiltstudy.org. Plese visit this website for more informtion on Seven Sisters quilt ptterns. Visit www.blocloc.com for video tutorils 1 The Seven Sisters design cn be
Exercise 1-1. The Sine Wave EXERCISE OBJECTIVE DISCUSSION OUTLINE. Relationship between a rotating phasor and a sine wave DISCUSSION
 Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
1/4" Multi-Turn Fully Sealed Container Cermet Trimmer
 www.vishy.om Vishy Sfernie 1/4" Multi-Turn Fully Seled Continer Cermet Trimmer Due to their squre shpe nd smll size (6.8 mm x 6.8 mm x 5 mm), the multi-turn trimmers of the series re idelly suited for
www.vishy.om Vishy Sfernie 1/4" Multi-Turn Fully Seled Continer Cermet Trimmer Due to their squre shpe nd smll size (6.8 mm x 6.8 mm x 5 mm), the multi-turn trimmers of the series re idelly suited for
ECE 274 Digital Logic Spring Digital Design. Combinational Logic Design Process and Common Combinational Components Digital Design
 ECE 27 Digitl Logi Spring 29 Comintionl Logi Design Proess n Common Comintionl Components Digitl Design 2.7 2. Digitl Design Chpter 2: Comintionl Logi Design Slies to ompn the tetook Digitl Design, irst
ECE 27 Digitl Logi Spring 29 Comintionl Logi Design Proess n Common Comintionl Components Digitl Design 2.7 2. Digitl Design Chpter 2: Comintionl Logi Design Slies to ompn the tetook Digitl Design, irst
The Math Learning Center PO Box 12929, Salem, Oregon Math Learning Center
 Resource Overview Quntile Mesure: Skill or Concept: 300Q Model the concept of ddition for sums to 10. (QT N 36) Model the concept of sutrction using numers less thn or equl to 10. (QT N 37) Write ddition
Resource Overview Quntile Mesure: Skill or Concept: 300Q Model the concept of ddition for sums to 10. (QT N 36) Model the concept of sutrction using numers less thn or equl to 10. (QT N 37) Write ddition
Algebra Practice. Dr. Barbara Sandall, Ed.D., and Travis Olson, M.S.
 By Dr. Brr Sndll, Ed.D., Dr. Melfried Olson, Ed.D., nd Trvis Olson, M.S. COPYRIGHT 2006 Mrk Twin Medi, Inc. ISBN 978-1-58037-754-6 Printing No. 404042-EB Mrk Twin Medi, Inc., Pulishers Distriuted y Crson-Dellos
By Dr. Brr Sndll, Ed.D., Dr. Melfried Olson, Ed.D., nd Trvis Olson, M.S. COPYRIGHT 2006 Mrk Twin Medi, Inc. ISBN 978-1-58037-754-6 Printing No. 404042-EB Mrk Twin Medi, Inc., Pulishers Distriuted y Crson-Dellos
Multi-beam antennas in a broadband wireless access system
 Multi-em ntenns in rodnd wireless ccess system Ulrik Engström, Mrtin Johnsson, nders Derneryd nd jörn Johnnisson ntenn Reserch Center Ericsson Reserch Ericsson SE-4 84 Mölndl Sweden E-mil: ulrik.engstrom@ericsson.com,
Multi-em ntenns in rodnd wireless ccess system Ulrik Engström, Mrtin Johnsson, nders Derneryd nd jörn Johnnisson ntenn Reserch Center Ericsson Reserch Ericsson SE-4 84 Mölndl Sweden E-mil: ulrik.engstrom@ericsson.com,
Triangle Definition of sin θ and cos θ
 Triangle Definition of sin θ and cos θ Then Consider the triangle ABC below. Let A be called θ. A HYP (hpotenuse) θ ADJ (side adjacent to the angle θ ) B C OPP (side opposite to the angle θ ) (SOH CAH
Triangle Definition of sin θ and cos θ Then Consider the triangle ABC below. Let A be called θ. A HYP (hpotenuse) θ ADJ (side adjacent to the angle θ ) B C OPP (side opposite to the angle θ ) (SOH CAH
3/8" Square Multi-Turn Cermet Trimmer
 www.vishy.om 3/8" Squre Multi-Turn Cermet Trimmer Vishy Sfernie ermet element. FEATURES Industril grde The is smll size trimmer - 3/8" x 3/8" x 3/16" - nswering PC ord mounting requirements. Five versions
www.vishy.om 3/8" Squre Multi-Turn Cermet Trimmer Vishy Sfernie ermet element. FEATURES Industril grde The is smll size trimmer - 3/8" x 3/8" x 3/16" - nswering PC ord mounting requirements. Five versions
13.4 Chapter 13: Trigonometric Ratios and Functions. Section 13.4
 13.4 Chapter 13: Trigonometric Ratios and Functions Section 13.4 1 13.4 Chapter 13: Trigonometric Ratios and Functions Section 13.4 2 Key Concept Section 13.4 3 Key Concept Section 13.4 4 Key Concept Section
13.4 Chapter 13: Trigonometric Ratios and Functions Section 13.4 1 13.4 Chapter 13: Trigonometric Ratios and Functions Section 13.4 2 Key Concept Section 13.4 3 Key Concept Section 13.4 4 Key Concept Section
Homework #1 due Monday at 6pm. White drop box in Student Lounge on the second floor of Cory. Tuesday labs cancelled next week
 Announcements Homework #1 due Mondy t 6pm White drop ox in Student Lounge on the second floor of Cory Tuesdy ls cncelled next week Attend your other l slot Books on reserve in Bechtel Hmley, 2 nd nd 3
Announcements Homework #1 due Mondy t 6pm White drop ox in Student Lounge on the second floor of Cory Tuesdy ls cncelled next week Attend your other l slot Books on reserve in Bechtel Hmley, 2 nd nd 3
MATH 118 PROBLEM SET 6
 MATH 118 PROBLEM SET 6 WASEEM LUTFI, GABRIEL MATSON, AND AMY PIRCHER Section 1 #16: Show tht if is qudrtic residue modulo m, nd b 1 (mod m, then b is lso qudrtic residue Then rove tht the roduct of the
MATH 118 PROBLEM SET 6 WASEEM LUTFI, GABRIEL MATSON, AND AMY PIRCHER Section 1 #16: Show tht if is qudrtic residue modulo m, nd b 1 (mod m, then b is lso qudrtic residue Then rove tht the roduct of the
(1) Non-linear system
 Liner vs. non-liner systems in impednce mesurements I INTRODUCTION Electrochemicl Impednce Spectroscopy (EIS) is n interesting tool devoted to the study of liner systems. However, electrochemicl systems
Liner vs. non-liner systems in impednce mesurements I INTRODUCTION Electrochemicl Impednce Spectroscopy (EIS) is n interesting tool devoted to the study of liner systems. However, electrochemicl systems
Sequential Logic (2) Synchronous vs Asynchronous Sequential Circuit. Clock Signal. Synchronous Sequential Circuits. FSM Overview 9/10/12
 9//2 Sequentil (2) ENGG5 st Semester, 22 Dr. Hden So Deprtment of Electricl nd Electronic Engineering http://www.eee.hku.hk/~engg5 Snchronous vs Asnchronous Sequentil Circuit This Course snchronous Sequentil
9//2 Sequentil (2) ENGG5 st Semester, 22 Dr. Hden So Deprtment of Electricl nd Electronic Engineering http://www.eee.hku.hk/~engg5 Snchronous vs Asnchronous Sequentil Circuit This Course snchronous Sequentil
9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations
 54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
4.2 Proving and Applying
 YOU WILL NEED alulator ruler EXPLORE 4.2 Proving and Applying the Sine and Cosine Laws for Obtuse Triangles An isoseles obtuse triangle has one angle that measures 120 and one side length that is 5 m.
YOU WILL NEED alulator ruler EXPLORE 4.2 Proving and Applying the Sine and Cosine Laws for Obtuse Triangles An isoseles obtuse triangle has one angle that measures 120 and one side length that is 5 m.
Student Book SERIES. Fractions. Name
 D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
So Many Possibilities page 1 of 2
 Otober Solving Problems Ativities & So Mny Possibilities pge of Use the blnk spe to solve eh problem. Show ll your work inluding numbers, words, or lbeled skethes. Write omplete sentene below your work
Otober Solving Problems Ativities & So Mny Possibilities pge of Use the blnk spe to solve eh problem. Show ll your work inluding numbers, words, or lbeled skethes. Write omplete sentene below your work
Spiral Tilings with C-curves
 Spirl Tilings with -curves Using ombintorics to Augment Trdition hris K. Plmer 19 North Albny Avenue hicgo, Illinois, 0 chris@shdowfolds.com www.shdowfolds.com Abstrct Spirl tilings used by rtisns through
Spirl Tilings with -curves Using ombintorics to Augment Trdition hris K. Plmer 19 North Albny Avenue hicgo, Illinois, 0 chris@shdowfolds.com www.shdowfolds.com Abstrct Spirl tilings used by rtisns through
Understanding Three-Phase Transformers
 PDH ourse E450 (4 PDH) Understnding Three-Phse Trnsformers Rlph Fehr, Ph.D., P.E. 2014 PDH Online PDH enter 5272 Medow Esttes Drive Firfx, V 22030-6658 Phone & Fx: 703-988-0088 www.pdhonline.org www.pdhenter.om
PDH ourse E450 (4 PDH) Understnding Three-Phse Trnsformers Rlph Fehr, Ph.D., P.E. 2014 PDH Online PDH enter 5272 Medow Esttes Drive Firfx, V 22030-6658 Phone & Fx: 703-988-0088 www.pdhonline.org www.pdhenter.om
Positron Emission Tomography (PET) Images
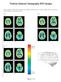 Positron Emission Tomogrphy (PET) Imges Eh set of PET imges elow ontins four imges of humn rin. The four imges show ross-setions tken t ifferent levels of the rin. Set 1 Set 4 Set 5 Set 2 Set 6 Set 3 highest
Positron Emission Tomogrphy (PET) Imges Eh set of PET imges elow ontins four imges of humn rin. The four imges show ross-setions tken t ifferent levels of the rin. Set 1 Set 4 Set 5 Set 2 Set 6 Set 3 highest
ASY P.O. BOX 729 TERRELL, TEXAS / PAGE 1 OF 13 SAM
 203 Madix Inc., ll rights reserved ommon Parts 2 MXI GRI WIRE GRI SHELF WITH (GPWGS) MXI GRI FIXTURE PNEL (GPWFP) FIXTURE PNELS RE USE S EN SUPPORT. SHELF N E USE NYWHERE. MXI GRI REINFORMENT R 3 (GPR)
203 Madix Inc., ll rights reserved ommon Parts 2 MXI GRI WIRE GRI SHELF WITH (GPWGS) MXI GRI FIXTURE PNEL (GPWFP) FIXTURE PNELS RE USE S EN SUPPORT. SHELF N E USE NYWHERE. MXI GRI REINFORMENT R 3 (GPR)
Unilateral and equitransitive tilings by squares of four sizes
 Also ville t http://m-journl.eu ISSN 1855-3966 (printe en.), ISSN 1855-3974 (eletroni en.) ARS MATHEMATICA CONTEMPORANEA 10 (2015) 135 167 Unilterl n equitrnsitive tilings y squres of four sizes Csey Mnn
Also ville t http://m-journl.eu ISSN 1855-3966 (printe en.), ISSN 1855-3974 (eletroni en.) ARS MATHEMATICA CONTEMPORANEA 10 (2015) 135 167 Unilterl n equitrnsitive tilings y squres of four sizes Csey Mnn
1/4" Multi-Turn Fully Sealed Container Cermet Trimmer
 1/4" Multi-Turn Fully Seled Continer Cermet Trimmer Due to their squre shpe nd smll size (6.8 mm x 6.8 mm x 5 mm), the multi-turn trimmers of the series re idelly suited for PCB use, enling high density
1/4" Multi-Turn Fully Seled Continer Cermet Trimmer Due to their squre shpe nd smll size (6.8 mm x 6.8 mm x 5 mm), the multi-turn trimmers of the series re idelly suited for PCB use, enling high density
Evaluating territories of Go positions with capturing races
 Gmes of No Chne 4 MSRI Pulitions Volume 63, 2015 Evluting territories of Go positions with pturing res TEIGO NAKAMURA In nlysing pturing res, or semeis, we hve een fousing on the method to find whih plyer
Gmes of No Chne 4 MSRI Pulitions Volume 63, 2015 Evluting territories of Go positions with pturing res TEIGO NAKAMURA In nlysing pturing res, or semeis, we hve een fousing on the method to find whih plyer
Vector Calculus. 1 Line Integrals
 Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Section 17.2: Line Integrals. 1 Objectives. 2 Assignments. 3 Maple Commands. 1. Compute line integrals in IR 2 and IR Read Section 17.
 Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Applications of a New Property of Conics to Architecture: An Alternative Design Project for Rio de Janeiro Metropolitan Cathedral
 Jun V. Mrtín Zorrquino Frneso Grnero odrígue José uis Cno Mrtín Applitions of New Property of Conis to Arhiteture: An Alterntive Design Projet for io de Jneiro Metropolitn Cthedrl This pper desries the
Jun V. Mrtín Zorrquino Frneso Grnero odrígue José uis Cno Mrtín Applitions of New Property of Conis to Arhiteture: An Alterntive Design Projet for io de Jneiro Metropolitn Cthedrl This pper desries the
Translate and Classify Conic Sections
 TEKS 9.6 A.5.A, A.5.B, A.5.D, A.5.E Trnslte nd Clssif Conic Sections Before You grphed nd wrote equtions of conic sections. Now You will trnslte conic sections. Wh? So ou cn model motion, s in E. 49. Ke
TEKS 9.6 A.5.A, A.5.B, A.5.D, A.5.E Trnslte nd Clssif Conic Sections Before You grphed nd wrote equtions of conic sections. Now You will trnslte conic sections. Wh? So ou cn model motion, s in E. 49. Ke
MATHEMATICS. Student Booklet
 GRADE 6 ASSESSMENT OF READING, WRITING AND MATHEMATICS, 2004 2005 Stuent Booklet MATHEMATICS Plese note: The formt of these ooklets is slightly ifferent from tht use for the ssessment. The items themselves
GRADE 6 ASSESSMENT OF READING, WRITING AND MATHEMATICS, 2004 2005 Stuent Booklet MATHEMATICS Plese note: The formt of these ooklets is slightly ifferent from tht use for the ssessment. The items themselves
FP2 POLAR COORDINATES: PAST QUESTIONS
 FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
Algorithms for Memory Hierarchies Lecture 14
 Algorithms for emory Hierrchies Lecture 4 Lecturer: Nodri Sitchinv Scribe: ichel Hmnn Prllelism nd Cche Obliviousness The combintion of prllelism nd cche obliviousness is n ongoing topic of reserch, in
Algorithms for emory Hierrchies Lecture 4 Lecturer: Nodri Sitchinv Scribe: ichel Hmnn Prllelism nd Cche Obliviousness The combintion of prllelism nd cche obliviousness is n ongoing topic of reserch, in
University of North Carolina-Charlotte Department of Electrical and Computer Engineering ECGR 4143/5195 Electrical Machinery Fall 2009
 Problem 1: Using DC Mchine University o North Crolin-Chrlotte Deprtment o Electricl nd Computer Engineering ECGR 4143/5195 Electricl Mchinery Fll 2009 Problem Set 4 Due: Thursdy October 8 Suggested Reding:
Problem 1: Using DC Mchine University o North Crolin-Chrlotte Deprtment o Electricl nd Computer Engineering ECGR 4143/5195 Electricl Mchinery Fll 2009 Problem Set 4 Due: Thursdy October 8 Suggested Reding:
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES
 MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
Francis Gaspalou Second edition of February 10, 2012 (First edition on January 28, 2012) HOW MANY SQUARES ARE THERE, Mr TARRY?
 Frncis Gslou Second edition of Ferury 10, 2012 (First edition on Jnury 28, 2012) HOW MANY SQUARES ARE THERE, Mr TARRY? ABSTRACT In this er, I enumerte ll the 8x8 imgic sures given y the Trry s ttern. This
Frncis Gslou Second edition of Ferury 10, 2012 (First edition on Jnury 28, 2012) HOW MANY SQUARES ARE THERE, Mr TARRY? ABSTRACT In this er, I enumerte ll the 8x8 imgic sures given y the Trry s ttern. This
Trigonometric ratios 9B 1 a d b 2 a c b
 Trigonometric ratios 9B 1 a a Using sin A sin B 8 sin 72 sin 30 8sin 72 sin 30 As 72 > 30, > 8 cm 15.2 cm ( ) ABC 180 68.4 + 83.7 27.9 Using a 9.8 sin 27.9 sin 83.7 9.8sin 27.9 a sin 83.7 4.61 cm ( ) 2
Trigonometric ratios 9B 1 a a Using sin A sin B 8 sin 72 sin 30 8sin 72 sin 30 As 72 > 30, > 8 cm 15.2 cm ( ) ABC 180 68.4 + 83.7 27.9 Using a 9.8 sin 27.9 sin 83.7 9.8sin 27.9 a sin 83.7 4.61 cm ( ) 2
Section 10.2 Graphing Polar Equations
 Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
Experiment 8 Series DC Motor (II)
 Ojectives To control the speed of loded series dc motor y chnging rmture voltge. To control the speed of loded series dc motor y dding resistnce in prllel with the rmture circuit. To control the speed
Ojectives To control the speed of loded series dc motor y chnging rmture voltge. To control the speed of loded series dc motor y dding resistnce in prllel with the rmture circuit. To control the speed
Unit 5. Algebra 2. Name:
 Unit 5 Algebra 2 Name: 12.1 Day 1: Trigonometric Functions in Right Triangles Vocabulary, Main Topics, and Questions Definitions, Diagrams and Examples Theta Opposite Side of an Angle Adjacent Side of
Unit 5 Algebra 2 Name: 12.1 Day 1: Trigonometric Functions in Right Triangles Vocabulary, Main Topics, and Questions Definitions, Diagrams and Examples Theta Opposite Side of an Angle Adjacent Side of
Name: A Trigonometric Review June 2012
 Name: A Trigonometric Review June 202 This homework will prepare you for in-class work tomorrow on describing oscillations. If you need help, there are several resources: tutoring on the third floor of
Name: A Trigonometric Review June 202 This homework will prepare you for in-class work tomorrow on describing oscillations. If you need help, there are several resources: tutoring on the third floor of
Discontinued AN6262N, AN6263N. (planed maintenance type, maintenance type, planed discontinued typed, discontinued type)
 ICs for Cssette, Cssette Deck ANN, ANN Puse Detection s of Rdio Cssette, Cssette Deck Overview The ANN nd the ANN re the puse detection integrted circuits which select the progrm on the cssette tpe. In
ICs for Cssette, Cssette Deck ANN, ANN Puse Detection s of Rdio Cssette, Cssette Deck Overview The ANN nd the ANN re the puse detection integrted circuits which select the progrm on the cssette tpe. In
Dataflow Language Model. DataFlow Models. Applications of Dataflow. Dataflow Languages. Kahn process networks. A Kahn Process (1)
 The slides contin revisited mterils from: Peter Mrwedel, TU Dortmund Lothr Thiele, ETH Zurich Frnk Vhid, University of liforni, Riverside Dtflow Lnguge Model Drsticlly different wy of looking t computtion:
The slides contin revisited mterils from: Peter Mrwedel, TU Dortmund Lothr Thiele, ETH Zurich Frnk Vhid, University of liforni, Riverside Dtflow Lnguge Model Drsticlly different wy of looking t computtion:
Synchronous Machine Parameter Measurement
 Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
Abdominal Wound Closure Forceps
 Inventor: Crlson, Mrk A. My 25, 2007 Adominl Wound Closure Foreps Astrt. The devie is modifition of stndrd tissue foreps for use during losure of dominl wounds mde for surgil proedure. The modifition onsists
Inventor: Crlson, Mrk A. My 25, 2007 Adominl Wound Closure Foreps Astrt. The devie is modifition of stndrd tissue foreps for use during losure of dominl wounds mde for surgil proedure. The modifition onsists
Study Guide # Vectors in R 2 and R 3. (a) v = a, b, c = a i + b j + c k; vector addition and subtraction geometrically using parallelograms
 Study Guide # 1 MA 26100 - Fll 2018 1. Vectors in R 2 nd R 3 () v =, b, c = i + b j + c k; vector ddition nd subtrction geometriclly using prllelogrms spnned by u nd v; length or mgnitude of v =, b, c,
Study Guide # 1 MA 26100 - Fll 2018 1. Vectors in R 2 nd R 3 () v =, b, c = i + b j + c k; vector ddition nd subtrction geometriclly using prllelogrms spnned by u nd v; length or mgnitude of v =, b, c,
Synchronous Machine Parameter Measurement
 Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
CS2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2005
 CS2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2005 EXPERIMENT 1 FUNDAMENTALS 1. GOALS : Lern how to develop cr lrm digitl circuit during which the following re introduced : CS2204 l fundmentls, nd
CS2204 DIGITAL LOGIC & STATE MACHINE DESIGN SPRING 2005 EXPERIMENT 1 FUNDAMENTALS 1. GOALS : Lern how to develop cr lrm digitl circuit during which the following re introduced : CS2204 l fundmentls, nd
