The Pythagorean Theorem
|
|
|
- Coral Bell
- 5 years ago
- Views:
Transcription
1 . The Pythagorean Theorem Goals Draw squares on the legs of the triangle. Deduce the Pythagorean Theorem through exploration Use the Pythagorean Theorem to find unknown side lengths of right triangles In this problem, students collect data about the areas of squares on the sides of a right triangle. They use patterns in their data to conjecture that the sum of the areas of the two smaller squares equals the area of the largest square. Launch. To introduce the topic, draw a right triangle below on a dot grid at the board or overhead. What kind of triangle have I drawn? (A right triangle) Explain that in a right triangle, the two sides that form the right angle are called the legs of the right triangle. The side opposite the right angle is called the hypotenuse. What are the lengths of the two legs of this triangle? ( unit) How can we find the length of the hypotenuse of the triangle? (Draw a square using this segment as a side. Then, find the area of the square and take its square root.) What are the areas of the squares on the legs? (Both squares have an area of square unit.) What is the area of the square on the hypotenuse? ( square units) Students may notice that the sum of the area of the squares on the legs is equal to the area of the square on the hypotenuse, but don t push for this observation at this time. You might say: In Problem., you will be looking for a relationship among the three squares that can be drawn on the sides of a right triangle. It will help to organize your work in a table so that you can look for patterns. Have students work in groups of three or four. Explore. Ask that each student complete a table. Encourage the students in each group to share the work, with each student finding the areas for two or three of the right triangles. Check to see that students are correctly drawing the squares on the right triangles. Summarize. Ask the class to discuss the patterns they see in the table. They should notice that the sum of the areas of the squares on the legs is equal to the area of the square on the hypotenuse. What conjecture can you make about your results? (When you add the areas of the squares on the legs, you get the area of the square on the hypotenuse.) This pattern is called the Pythagorean Theorem. 5 Looking for Pythagoras
2 Draw and label a right triangle as shown below. a Suppose a right triangle has legs of lengths a and b and a hypotenuse of length c. Using these letters, can you state the Pythagorean Theorem in a general way? (If a and b are the lengths of the legs of a right triangle and c is the length of the hypotenuse, then a + b = c.) Do you think the Pythagorean Theorem will work for triangles that are not right triangles? To help the class explore this question, draw the triangle shown below on the board or overhead (or have the class try this example on their own). Use a corner of a sheet of paper to verify that the triangle does not contain a right angle. b Then, draw squares on each side of the triangle. c We have shown that this triangle is not a right triangle. What are the areas of the squares on its sides? (5, 0, and 5 square units) Is the sum of the areas of the squares on the shorter sides equal to the area of the square on the longest side? (No; ) Next, ask the class this question: Do you think the Pythagorean Theorem is true for all right triangles, even if the sides are not whole numbers? The theorem is true for all right triangles. To help the class explore this, you may want to do ACE Exercises and as a class. The triangle in Exercise has leg lengths "5 units and "5 units, and hypotenuse length "0. The squares of these side lengths are 5, 5, and 0 and = 0. This shows that the Pythagorean Theorem applies to a right triangle with side lengths that are not whole numbers. A proof that shows the theorem is true for all right triangles is developed in the next problem. The Pythagorean Theorem is useful for finding unknown side lengths in a right triangle. In this spirit, you could wrap up by having students add a column to their tables, labeled Length of Hypotenuse. Fill in this column together, or give students a short period of time to complete it themselves and then check the results as a class. Suggested Question Choose one of the right triangles in the table, list the lengths of the three sides, and ask students what the Pythagorean Theorem says about these lengths. The lengths of the sides of a right triangle are,, and ". What does the Pythagorean Theorem say about these lengths? ( + = ("), or + = ) Repeat the question for lengths 5,, and. INVESTIGATION Investigation The Pythagorean Theorem 5
3 5 Looking for Pythagoras
4 . The Pythagorean Theorem At a Glance PACING days Mathematical Goals Deduce the Pythagorean Theorem through exploration Use the Pythagorean Theorem to find unknown side lengths of right triangles Launch Draw a tilted line segment on a dot grid at the board or overhead. Ask: How can we find the length of this line segment? Using the original line segment as a hypotenuse, draw two line segments to make a right triangle. What kind of triangle have I drawn? Explain that in a right triangle, the two sides that form the right angle are called the legs of the right triangle. The side opposite the right angle is called the hypotenuse. What are the lengths of the two legs of this triangle? What are the areas of the squares on the legs? What is the area of the square on the hypotenuse? Have students work in groups of three or four on the problem. Materials Dot paper Centimeter rulers Vocabulary hypotenuse legs Explore Ask that each student complete a table. Encourage the students in each group to share the work, with each student finding the areas for two or three of the right triangles. As you circulate, check to see that students are correctly drawing the squares on the right triangles. Discuss the patterns in the table. What conjecture can you make about your results? This pattern is called the Pythagorean Theorem. Suppose a right triangle has legs of lengths a and b and a hypotenuse of length c. Using these letters, can you state the Pythagorean Theorem in a general way? Do you think the Pythagorean Theorem will work for triangles that are not right triangles? Help the class explore this question by drawing a non-right triangle and then drawing squares on the sides. Then ask: Investigation The Pythagorean Theorem 55
5 Summarize Do you think the Pythagorean Theorem is true for all right triangles, even if the sides are not whole numbers? The theorem is true for all right triangles. To help the class explore this, you may want to do ACE Exercises and as a class. You could wrap up by having students add a column to their tables, labeled Length of Hypotenuse. Fill in this column together, or give students time to complete it themselves and then check the results as a class. Choose one of the right triangles in the table, list the lengths of the three sides, and ask students what the Pythagorean Theorem says about these lengths. Materials Student notebooks Vocabulary conjecture Pythagorean Theorem ACE Assignment Guide for Problem. Core,, 5, 6, 8, Other Applications,, 7,, Adapted For suggestions about adapting Exercises 8 and other ACE exercises, see the CMP Special Needs Handbook. Connecting to Prior Units 8 : Filling and Wrapping Answers to Problem. A. (Figure ) B. The area of the square on the hypotenuse is equal to the sum of the areas of the squares on the legs. C. Possible answer: If the legs of a right triangle are units and unit, then the area of the square on the hypotenuse is 7 units because 6 + = Figure Length of Leg (units) Length of Leg (units) on Leg (units ) on Leg (units ) on Hypotenuse (units ) Looking for Pythagoras
Looking for Pythagoras An Investigation of the Pythagorean Theorem
 Looking for Pythagoras An Investigation of the Pythagorean Theorem I2t2 2006 Stephen Walczyk Grade 8 7-Day Unit Plan Tools Used: Overhead Projector Overhead markers TI-83 Graphing Calculator (& class set)
Looking for Pythagoras An Investigation of the Pythagorean Theorem I2t2 2006 Stephen Walczyk Grade 8 7-Day Unit Plan Tools Used: Overhead Projector Overhead markers TI-83 Graphing Calculator (& class set)
The Pythagorean Theorem
 ! The Pythagorean Theorem Recall that a right triangle is a triangle with a right, or 90, angle. The longest side of a right triangle is the side opposite the right angle. We call this side the hypotenuse
! The Pythagorean Theorem Recall that a right triangle is a triangle with a right, or 90, angle. The longest side of a right triangle is the side opposite the right angle. We call this side the hypotenuse
The Pythagorean Theorem and Right Triangles
 The Pythagorean Theorem and Right Triangles Student Probe Triangle ABC is a right triangle, with right angle C. If the length of and the length of, find the length of. Answer: the length of, since and
The Pythagorean Theorem and Right Triangles Student Probe Triangle ABC is a right triangle, with right angle C. If the length of and the length of, find the length of. Answer: the length of, since and
Pythagorean Theorem Unit
 Pythagorean Theorem Unit TEKS covered: ~ Square roots and modeling square roots, 8.1(C); 7.1(C) ~ Real number system, 8.1(A), 8.1(C); 7.1(A) ~ Pythagorean Theorem and Pythagorean Theorem Applications,
Pythagorean Theorem Unit TEKS covered: ~ Square roots and modeling square roots, 8.1(C); 7.1(C) ~ Real number system, 8.1(A), 8.1(C); 7.1(A) ~ Pythagorean Theorem and Pythagorean Theorem Applications,
Challenging Students to Discover the Pythagorean Relationship
 Brought to you by YouthBuild USA Teacher Fellows! Challenging Students to Discover the Pythagorean Relationship A Common Core-Aligned Lesson Plan to use in your Classroom Author Richard Singer, St. Louis
Brought to you by YouthBuild USA Teacher Fellows! Challenging Students to Discover the Pythagorean Relationship A Common Core-Aligned Lesson Plan to use in your Classroom Author Richard Singer, St. Louis
SPIRIT 2.0 Lesson: How Far Am I Traveling?
 SPIRIT 2.0 Lesson: How Far Am I Traveling? ===============================Lesson Header ============================ Lesson Title: How Far Am I Traveling? Draft Date: June 12, 2008 1st Author (Writer):
SPIRIT 2.0 Lesson: How Far Am I Traveling? ===============================Lesson Header ============================ Lesson Title: How Far Am I Traveling? Draft Date: June 12, 2008 1st Author (Writer):
THE PYTHAGOREAN SPIRAL PROJECT
 THE PYTHAGOREAN SPIRAL PROJECT A Pythagorean Spiral is a series of right triangles arranged in a spiral configuration such that the hypotenuse of one right triangle is a leg of the next right triangle.
THE PYTHAGOREAN SPIRAL PROJECT A Pythagorean Spiral is a series of right triangles arranged in a spiral configuration such that the hypotenuse of one right triangle is a leg of the next right triangle.
Set 6: Understanding the Pythagorean Theorem Instruction
 Instruction Goal: To provide opportunities for students to develop concepts and skills related to understanding that the Pythagorean theorem is a statement about areas of squares on the sides of a right
Instruction Goal: To provide opportunities for students to develop concepts and skills related to understanding that the Pythagorean theorem is a statement about areas of squares on the sides of a right
3.9. Pythagorean Theorem Stop the Presses. My Notes ACTIVITY
 Pythagorean Theorem SUGGESTED LEARNING STRATEGIES: Marking the Text, Predict and Confirm, Shared Reading Jayla and Sidney are co-editors-in-chief of the school yearbook. They have just finished the final
Pythagorean Theorem SUGGESTED LEARNING STRATEGIES: Marking the Text, Predict and Confirm, Shared Reading Jayla and Sidney are co-editors-in-chief of the school yearbook. They have just finished the final
How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr.
 Common Core Standard: 8.G.6, 8.G.7 How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.2 What Is Special
Common Core Standard: 8.G.6, 8.G.7 How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.2 What Is Special
Representing Square Numbers. Use materials to represent square numbers. A. Calculate the number of counters in this square array.
 1.1 Student book page 4 Representing Square Numbers You will need counters a calculator Use materials to represent square numbers. A. Calculate the number of counters in this square array. 5 5 25 number
1.1 Student book page 4 Representing Square Numbers You will need counters a calculator Use materials to represent square numbers. A. Calculate the number of counters in this square array. 5 5 25 number
Square Roots and the Pythagorean Theorem
 UNIT 1 Square Roots and the Pythagorean Theorem Just for Fun What Do You Notice? Follow the steps. An example is given. Example 1. Pick a 4-digit number with different digits. 3078 2. Find the greatest
UNIT 1 Square Roots and the Pythagorean Theorem Just for Fun What Do You Notice? Follow the steps. An example is given. Example 1. Pick a 4-digit number with different digits. 3078 2. Find the greatest
1.1 The Pythagorean Theorem
 1.1 The Pythagorean Theorem Strand Measurement and Geometry Overall Expectations MGV.02: solve problems involving the measurements of two-dimensional shapes and the volumes of three-dimensional figures;
1.1 The Pythagorean Theorem Strand Measurement and Geometry Overall Expectations MGV.02: solve problems involving the measurements of two-dimensional shapes and the volumes of three-dimensional figures;
Student Instruction Sheet: Unit 4 Lesson 1. Pythagorean Theorem
 Student Instruction Sheet: Unit 4 Lesson 1 Suggested time: 75 minutes Pythagorean Theorem What s important in this lesson: In this lesson you will learn the Pythagorean Theorem and how to apply the theorem
Student Instruction Sheet: Unit 4 Lesson 1 Suggested time: 75 minutes Pythagorean Theorem What s important in this lesson: In this lesson you will learn the Pythagorean Theorem and how to apply the theorem
Catty Corner. Side Lengths in Two and. Three Dimensions
 Catty Corner Side Lengths in Two and 4 Three Dimensions WARM UP A 1. Imagine that the rectangular solid is a room. An ant is on the floor situated at point A. Describe the shortest path the ant can crawl
Catty Corner Side Lengths in Two and 4 Three Dimensions WARM UP A 1. Imagine that the rectangular solid is a room. An ant is on the floor situated at point A. Describe the shortest path the ant can crawl
Mathematical Construction
 Mathematical Construction Full illustrated instructions for the two bisectors: Perpendicular bisector Angle bisector Full illustrated instructions for the three triangles: ASA SAS SSS Note: These documents
Mathematical Construction Full illustrated instructions for the two bisectors: Perpendicular bisector Angle bisector Full illustrated instructions for the three triangles: ASA SAS SSS Note: These documents
UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet
 Name Period Date UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet 24.1 The Pythagorean Theorem Explore the Pythagorean theorem numerically, algebraically, and geometrically. Understand a proof
Name Period Date UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet 24.1 The Pythagorean Theorem Explore the Pythagorean theorem numerically, algebraically, and geometrically. Understand a proof
Lesson 6.1 Skills Practice
 Lesson 6.1 Skills Practice Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Vocabulary Match each definition to its corresponding term. 1. A mathematical statement
Lesson 6.1 Skills Practice Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Vocabulary Match each definition to its corresponding term. 1. A mathematical statement
Exploring the Pythagorean Theorem
 Exploring the Pythagorean Theorem Lesson 11 Mathematics Objectives Students will analyze relationships to develop the Pythagorean Theorem. Students will find missing sides in right triangles using the
Exploring the Pythagorean Theorem Lesson 11 Mathematics Objectives Students will analyze relationships to develop the Pythagorean Theorem. Students will find missing sides in right triangles using the
1. 1 Square Numbers and Area Models (pp. 6-10)
 Math 8 Unit 1 Notes Name: 1. 1 Square Numbers and Area Models (pp. 6-10) square number: the product of a number multiplied by itself; for example, 25 is the square of 5 perfect square: a number that is
Math 8 Unit 1 Notes Name: 1. 1 Square Numbers and Area Models (pp. 6-10) square number: the product of a number multiplied by itself; for example, 25 is the square of 5 perfect square: a number that is
Getting Triggy With It
 Getting Triggy With It Date: 15 May 2013 Topic: Pythagorean Theorem and Trigonometric Ratios Class: Grade 9 Ability Level: Mixed Ability Teacher: Mr. Cyrus Alvarez LESSON OBJECTIVES: At the end of the
Getting Triggy With It Date: 15 May 2013 Topic: Pythagorean Theorem and Trigonometric Ratios Class: Grade 9 Ability Level: Mixed Ability Teacher: Mr. Cyrus Alvarez LESSON OBJECTIVES: At the end of the
8.2 Slippery Slopes. A Solidify Understanding Task
 7 8.2 Slippery Slopes A Solidify Understanding Task CC BY https://flic.kr/p/kfus4x While working on Is It Right? in the previous module you looked at several examples that lead to the conclusion that the
7 8.2 Slippery Slopes A Solidify Understanding Task CC BY https://flic.kr/p/kfus4x While working on Is It Right? in the previous module you looked at several examples that lead to the conclusion that the
The Pythagorean Theorem 8.6.C
 ? LESSON 8.1 The Pythagorean Theorem ESSENTIAL QUESTION Expressions, equations, and relationships 8.6.C Use models and diagrams to explain the Pythagorean Theorem. 8.7.C Use the Pythagorean Theorem...
? LESSON 8.1 The Pythagorean Theorem ESSENTIAL QUESTION Expressions, equations, and relationships 8.6.C Use models and diagrams to explain the Pythagorean Theorem. 8.7.C Use the Pythagorean Theorem...
IM 8 Ch Does It Always Work. Common Core Standard: Is the triangle a right triangle? Who is Pythagoras? CPM Materials modified by Mr.
 Common Core Standard: 8.G.6 Is the triangle a right triangle? Who is Pythagoras? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.7 Does It Always Work? Date: Learning Target By the end of the period,
Common Core Standard: 8.G.6 Is the triangle a right triangle? Who is Pythagoras? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.7 Does It Always Work? Date: Learning Target By the end of the period,
Concept: Pythagorean Theorem Name:
 Concept: Pythagorean Theorem Name: Interesting Fact: The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations. This famous theorem is named for the Greek mathematician and
Concept: Pythagorean Theorem Name: Interesting Fact: The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations. This famous theorem is named for the Greek mathematician and
Deriving the General Equation of a Circle
 Deriving the General Equation of a Circle Standard Addressed in this Task MGSE9-12.G.GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square
Deriving the General Equation of a Circle Standard Addressed in this Task MGSE9-12.G.GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square
GAP CLOSING. Powers and Roots. Intermediate / Senior Facilitator Guide
 GAP CLOSING Powers and Roots Intermediate / Senior Facilitator Guide Powers and Roots Diagnostic...5 Administer the diagnostic...5 Using diagnostic results to personalize interventions...5 Solutions...5
GAP CLOSING Powers and Roots Intermediate / Senior Facilitator Guide Powers and Roots Diagnostic...5 Administer the diagnostic...5 Using diagnostic results to personalize interventions...5 Solutions...5
Construction. Student Handbook
 Construction Essential Math Skills for the Apprentice Student Handbook Theory 2 Measurement In all trades the most commonly used tool is the tape measure. Understanding units of measurement is vital to
Construction Essential Math Skills for the Apprentice Student Handbook Theory 2 Measurement In all trades the most commonly used tool is the tape measure. Understanding units of measurement is vital to
In a right-angled triangle, the side opposite the right angle is called the hypotenuse.
 MATHEMATICAL APPLICATIONS 1 WEEK 14 NOTES & EXERCISES In a right-angled triangle, the side opposite the right angle is called the hypotenuse. The other two sides are named in relation to the angle in question,
MATHEMATICAL APPLICATIONS 1 WEEK 14 NOTES & EXERCISES In a right-angled triangle, the side opposite the right angle is called the hypotenuse. The other two sides are named in relation to the angle in question,
Predicting the Ones Digit
 . Predicting the Ones Digit Goals Eamine patterns in the eponential and standard forms of powers of whole numbers Use patterns in powers to estimate the ones digits for unknown powers In this problem,
. Predicting the Ones Digit Goals Eamine patterns in the eponential and standard forms of powers of whole numbers Use patterns in powers to estimate the ones digits for unknown powers In this problem,
Irrational Numbers Can In-Spiral You
 L e s l i e D. L e w i s Irrational Numbers Can In-Spiral You Introducing students to the Pytha - gorean theorem presents a natural context for investigating what irrational numbers are and how they differ
L e s l i e D. L e w i s Irrational Numbers Can In-Spiral You Introducing students to the Pytha - gorean theorem presents a natural context for investigating what irrational numbers are and how they differ
Your Task. Unit 3 (Chapter 1): Number Relationships. The 5 Goals of Chapter 1
 Unit 3 (Chapter 1): Number Relationships The 5 Goals of Chapter 1 I will be able to: model perfect squares and square roots use a variety of strategies to recognize perfect squares use a variety of strategies
Unit 3 (Chapter 1): Number Relationships The 5 Goals of Chapter 1 I will be able to: model perfect squares and square roots use a variety of strategies to recognize perfect squares use a variety of strategies
Pythagorean Theorem. 2.1 Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem... 45
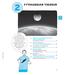 Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions.
 Student Outcomes Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions. Lesson Notes It is recommended that students have access to a calculator as they work
Student Outcomes Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions. Lesson Notes It is recommended that students have access to a calculator as they work
Lesson 3 Pre-Visit Perimeter and Area
 Lesson 3 Pre-Visit Perimeter and Area Objective: Students will be able to: Distinguish between area and perimeter. Calculate the perimeter of a polygon whose side lengths are given or can be determined.
Lesson 3 Pre-Visit Perimeter and Area Objective: Students will be able to: Distinguish between area and perimeter. Calculate the perimeter of a polygon whose side lengths are given or can be determined.
Create Your Own Triangles Learning Task
 Create Your Own Triangles Learning Task Supplies needed Heavy stock, smooth unlined paper for constructing triangles (unlined index cards, white or pastel colors are a good choice) Unlined paper (if students
Create Your Own Triangles Learning Task Supplies needed Heavy stock, smooth unlined paper for constructing triangles (unlined index cards, white or pastel colors are a good choice) Unlined paper (if students
Investigation. Triangle, Triangle, Triangle. Work with a partner.
 Investigation Triangle, Triangle, Triangle Work with a partner. Materials: centimetre ruler 1-cm grid paper scissors Part 1 On grid paper, draw a large right triangle. Make sure its base is along a grid
Investigation Triangle, Triangle, Triangle Work with a partner. Materials: centimetre ruler 1-cm grid paper scissors Part 1 On grid paper, draw a large right triangle. Make sure its base is along a grid
Concept: Pythagorean Theorem Name:
 Concept: Pythagorean Theorem Name: Interesting Fact: The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations. This famous theorem is named for the Greek mathematician and
Concept: Pythagorean Theorem Name: Interesting Fact: The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations. This famous theorem is named for the Greek mathematician and
Geometry. Teacher s Guide
 Geometry Teacher s Guide WALCH PUBLISHING Table of Contents To the Teacher.......................................................... vi Classroom Management..................................................
Geometry Teacher s Guide WALCH PUBLISHING Table of Contents To the Teacher.......................................................... vi Classroom Management..................................................
E G 2 3. MATH 1012 Section 8.1 Basic Geometric Terms Bland
 MATH 1012 Section 8.1 Basic Geometric Terms Bland Point A point is a location in space. It has no length or width. A point is represented by a dot and is named by writing a capital letter next to the dot.
MATH 1012 Section 8.1 Basic Geometric Terms Bland Point A point is a location in space. It has no length or width. A point is represented by a dot and is named by writing a capital letter next to the dot.
2. Where might you find an example of a right angle in your home? How could you check that it is a right angle?
 Master 4.22 Extra Practice 1 Lesson 1: Naming Angles 1. Look at the angles in each of the shapes below. Which angles are acute, right, or obtuse angles? How do you know? 2. Where might you find an example
Master 4.22 Extra Practice 1 Lesson 1: Naming Angles 1. Look at the angles in each of the shapes below. Which angles are acute, right, or obtuse angles? How do you know? 2. Where might you find an example
GAP CLOSING. Powers and Roots. Intermediate / Senior Student Book GAP CLOSING. Powers and Roots. Intermediate / Senior Student Book
 GAP CLOSING Powers and Roots GAP CLOSING Powers and Roots Intermediate / Senior Student Book Intermediate / Senior Student Book Powers and Roots Diagnostic...3 Perfect Squares and Square Roots...6 Powers...
GAP CLOSING Powers and Roots GAP CLOSING Powers and Roots Intermediate / Senior Student Book Intermediate / Senior Student Book Powers and Roots Diagnostic...3 Perfect Squares and Square Roots...6 Powers...
STUDENT'S BOOKLET. Pythagoras Trips. Contents. 1 Squares and Roots 2 Straight Moves. 3 Game of Vectors. Meeting 6 Student s Booklet
 Meeting 6 Student s Booklet Pythagoras Trips February 22 2017 @ UCI Contents 1 Squares and Roots 2 Straight Moves STUDENT'S BOOKLET 3 Game of Vectors 1 SQUARES AND ROOTS UCI Math CEO Meeting 6 (FEBRUARY
Meeting 6 Student s Booklet Pythagoras Trips February 22 2017 @ UCI Contents 1 Squares and Roots 2 Straight Moves STUDENT'S BOOKLET 3 Game of Vectors 1 SQUARES AND ROOTS UCI Math CEO Meeting 6 (FEBRUARY
( for 2 lessons) Key vocabulary: triangle, square, root, hypotenuse, leg, angle, side, length, equation
 LESSON: Pythagoras Theorem ( for 2 lessons) Level: Pre-intermediate, intermediate Learning objectives: to understand the relationship between the sides of right angled-triangle to solve problems using
LESSON: Pythagoras Theorem ( for 2 lessons) Level: Pre-intermediate, intermediate Learning objectives: to understand the relationship between the sides of right angled-triangle to solve problems using
8.2 Slippery Slopes. A Solidify Understanding Task
 SECONDARY MATH I // MODULE 8 7 8.2 Slippery Slopes A Solidify Understanding Task CC BY https://flic.kr/p/kfus4x While working on Is It Right? in the previous module you looked at several examples that
SECONDARY MATH I // MODULE 8 7 8.2 Slippery Slopes A Solidify Understanding Task CC BY https://flic.kr/p/kfus4x While working on Is It Right? in the previous module you looked at several examples that
FOM 11 Ch. 1 Practice Test Name: Inductive and Deductive Reasoning
 FOM 11 Ch. 1 Practice Test Name: Inductive and Deductive Reasoning Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Justin gathered the following evidence.
FOM 11 Ch. 1 Practice Test Name: Inductive and Deductive Reasoning Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Justin gathered the following evidence.
Lesson 12: Unique Triangles Two Sides and a Non-Included Angle
 Lesson 12: Unique Triangles Two Sides and a Non-Included Angle Classwork Exploratory Challenge 1. Use your tools to draw, provided cm, cm, and. Continue with the rest of the problem as you work on your
Lesson 12: Unique Triangles Two Sides and a Non-Included Angle Classwork Exploratory Challenge 1. Use your tools to draw, provided cm, cm, and. Continue with the rest of the problem as you work on your
The Basics: Geometric Structure
 Trinity University Digital Commons @ Trinity Understanding by Design: Complete Collection Understanding by Design Summer 6-2015 The Basics: Geometric Structure Danielle Kendrick Trinity University Follow
Trinity University Digital Commons @ Trinity Understanding by Design: Complete Collection Understanding by Design Summer 6-2015 The Basics: Geometric Structure Danielle Kendrick Trinity University Follow
c) What is the ratio of the length of the side of a square to the length of its diagonal? Is this ratio the same for all squares? Why or why not?
 Tennessee Department of Education Task: Ratios, Proportions, and Similar Figures 1. a) Each of the following figures is a square. Calculate the length of each diagonal. Do not round your answer. Geometry/Core
Tennessee Department of Education Task: Ratios, Proportions, and Similar Figures 1. a) Each of the following figures is a square. Calculate the length of each diagonal. Do not round your answer. Geometry/Core
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem
 5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem I. Lesson Objectives: -Students will be able to recall definitions of angles, how to measure angles, and measurement systems
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem I. Lesson Objectives: -Students will be able to recall definitions of angles, how to measure angles, and measurement systems
6.1 Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Can That Be Right? 6.3 Pythagoras to the Rescue
 Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
Grade 8 Module 3 Lessons 1 14
 Eureka Math 2015 2016 Grade 8 Module 3 Lessons 1 14 Eureka Math, A Story of R a t i o s Published by the non-profit Great Minds. Copyright 2015 Great Minds. No part of this work may be reproduced, distributed,
Eureka Math 2015 2016 Grade 8 Module 3 Lessons 1 14 Eureka Math, A Story of R a t i o s Published by the non-profit Great Minds. Copyright 2015 Great Minds. No part of this work may be reproduced, distributed,
and Transitional Comprehensive Curriculum. Geometry Unit 3: Parallel and Perpendicular Relationships
 Geometry Unit 3: Parallel and Perpendicular Relationships Time Frame: Approximately three weeks Unit Description This unit demonstrates the basic role played by Euclid s fifth postulate in geometry. Euclid
Geometry Unit 3: Parallel and Perpendicular Relationships Time Frame: Approximately three weeks Unit Description This unit demonstrates the basic role played by Euclid s fifth postulate in geometry. Euclid
Trigonometric identities
 Trigonometric identities An identity is an equation that is satisfied by all the values of the variable(s) in the equation. For example, the equation (1 + x) = 1 + x + x is an identity. If you replace
Trigonometric identities An identity is an equation that is satisfied by all the values of the variable(s) in the equation. For example, the equation (1 + x) = 1 + x + x is an identity. If you replace
You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion)
 Pre-Test Unit 7: Pythagorean Theorem KEY You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion) 1. What is the IF-THEN statement for the Pythagorean Theorem?
Pre-Test Unit 7: Pythagorean Theorem KEY You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion) 1. What is the IF-THEN statement for the Pythagorean Theorem?
6.1B Lesson: Building Triangles Given Three Measurements*
 6.1 Lesson: uilding Triangles Given Three Measurements* Name: Period: 1. ircle all the triangles with side lengths 8 and 5 and an included angle of 32. a. b. c. 2. ircle all the triangles with side lengths
6.1 Lesson: uilding Triangles Given Three Measurements* Name: Period: 1. ircle all the triangles with side lengths 8 and 5 and an included angle of 32. a. b. c. 2. ircle all the triangles with side lengths
Requesting a Reward. Goals. Launch 1.2. Explore
 . Requesting a Reward Goals Express a product of identical factors in both exponential form and standard form Gain an intuitive understanding of basic exponential growth patterns Begin to recognize exponential
. Requesting a Reward Goals Express a product of identical factors in both exponential form and standard form Gain an intuitive understanding of basic exponential growth patterns Begin to recognize exponential
1 Version 2.0. Related Below-Grade and Above-Grade Standards for Purposes of Planning for Vertical Scaling:
 Claim 1: Concepts and Procedures Students can explain and apply mathematical concepts and carry out mathematical procedures with precision and fluency. Content Domain: Geometry Target E [a]: Draw, construct,
Claim 1: Concepts and Procedures Students can explain and apply mathematical concepts and carry out mathematical procedures with precision and fluency. Content Domain: Geometry Target E [a]: Draw, construct,
Day 1: June 6, 2011 (Kristin, Shirley, Sheryle, Amber) 8:30 Norms, parking lot (Shirley) 8:40 Class builder (Sheryle) 8:50 PS 1 Materials: Rulers,
 Day 1: June 6, 2011 (Kristin, Shirley, Sheryle, Amber) 8:30 Norms, parking lot (Shirley) 8:40 Class builder (Sheryle) 8:50 PS 1 Materials: Rulers, protractors, colored pencils, shapes printed on colored
Day 1: June 6, 2011 (Kristin, Shirley, Sheryle, Amber) 8:30 Norms, parking lot (Shirley) 8:40 Class builder (Sheryle) 8:50 PS 1 Materials: Rulers, protractors, colored pencils, shapes printed on colored
INTERMEDIATE LEVEL MEASUREMENT
 INTERMEDIATE LEVEL MEASUREMENT TABLE OF CONTENTS Format & Background Information...3-6 Learning Experience 1- Getting Started...6-7 Learning Experience 2 - Cube and Rectangular Prisms...8 Learning Experience
INTERMEDIATE LEVEL MEASUREMENT TABLE OF CONTENTS Format & Background Information...3-6 Learning Experience 1- Getting Started...6-7 Learning Experience 2 - Cube and Rectangular Prisms...8 Learning Experience
NOTES AND EXERCISES WEEK 9 AND 10
 ESSENTIAL MATHEMATICS 3 NOTES AND EXERCISES WEEK 9 AND 10 Scale Drawings A scale drawing is usually a reduction of a real object, such as a building, but can be an enlargement of a very small object, such
ESSENTIAL MATHEMATICS 3 NOTES AND EXERCISES WEEK 9 AND 10 Scale Drawings A scale drawing is usually a reduction of a real object, such as a building, but can be an enlargement of a very small object, such
ACCELERATED MATHEMATICS CHAPTER 14 PYTHAGOREAN THEOREM TOPICS COVERED: Simplifying Radicals Pythagorean Theorem Distance formula
 ACCELERATED MATHEMATICS CHAPTER 14 PYTHAGOREAN THEOREM TOPICS COVERED: Simplifying Radicals Pythagorean Theorem Distance formula Activity 14-1: Simplifying Radicals In this chapter, radicals are going
ACCELERATED MATHEMATICS CHAPTER 14 PYTHAGOREAN THEOREM TOPICS COVERED: Simplifying Radicals Pythagorean Theorem Distance formula Activity 14-1: Simplifying Radicals In this chapter, radicals are going
Model Perimeter. So, the perimeter of the figure is 16 units. centimeters. centimeters. centimeters. centimeters
 Lesson 11.1 Reteach Model Perimeter Perimeter is the distance around a figure. Find the perimeter of the figure. Step 1 Choose a unit to begin counting and label it 1. 1 1 unit Step 2 Count each unit around
Lesson 11.1 Reteach Model Perimeter Perimeter is the distance around a figure. Find the perimeter of the figure. Step 1 Choose a unit to begin counting and label it 1. 1 1 unit Step 2 Count each unit around
Paper Folding: Maximizing the Area of a Triangle Algebra 2
 Paper Folding: Maximizing the Area of a Triangle Algebra (This lesson was developed by Jan Baysden of Hoggard High School and Julie Fonvielle of Whiteville High School during the Leading to Success in
Paper Folding: Maximizing the Area of a Triangle Algebra (This lesson was developed by Jan Baysden of Hoggard High School and Julie Fonvielle of Whiteville High School during the Leading to Success in
In this section, you will learn the basic trigonometric identities and how to use them to prove other identities.
 4.6 Trigonometric Identities Solutions to equations that arise from real-world problems sometimes include trigonometric terms. One example is a trajectory problem. If a volleyball player serves a ball
4.6 Trigonometric Identities Solutions to equations that arise from real-world problems sometimes include trigonometric terms. One example is a trajectory problem. If a volleyball player serves a ball
Number Relationships. Chapter GOAL
 Chapter 1 Number Relationships GOAL You will be able to model perfect squares and square roots use a variety of strategies to recognize perfect squares use a variety of strategies to estimate and calculate
Chapter 1 Number Relationships GOAL You will be able to model perfect squares and square roots use a variety of strategies to recognize perfect squares use a variety of strategies to estimate and calculate
Special Geometry Exam, Fall 2008, W. Stephen Wilson. Mathematics Department, Johns Hopkins University
 Special eometry xam, all 008, W. Stephen Wilson. Mathematics epartment, Johns opkins University I agree to complete this exam without unauthorized assistance from any person, materials or device. Name
Special eometry xam, all 008, W. Stephen Wilson. Mathematics epartment, Johns opkins University I agree to complete this exam without unauthorized assistance from any person, materials or device. Name
Meet #5 March Intermediate Mathematics League of Eastern Massachusetts
 Meet #5 March 2008 Intermediate Mathematics League of Eastern Massachusetts Meet #5 March 2008 Category 1 Mystery 1. In the diagram to the right, each nonoverlapping section of the large rectangle is
Meet #5 March 2008 Intermediate Mathematics League of Eastern Massachusetts Meet #5 March 2008 Category 1 Mystery 1. In the diagram to the right, each nonoverlapping section of the large rectangle is
METHOD 1: METHOD 2: 4D METHOD 1: METHOD 2:
 4A Strategy: Count how many times each digit appears. There are sixteen 4s, twelve 3s, eight 2s, four 1s, and one 0. The sum of the digits is (16 4) + + (8 2) + (4 1) = 64 + 36 +16+4= 120. 4B METHOD 1:
4A Strategy: Count how many times each digit appears. There are sixteen 4s, twelve 3s, eight 2s, four 1s, and one 0. The sum of the digits is (16 4) + + (8 2) + (4 1) = 64 + 36 +16+4= 120. 4B METHOD 1:
Chapter 5. Drawing a cube. 5.1 One and two-point perspective. Math 4520, Spring 2015
 Chapter 5 Drawing a cube Math 4520, Spring 2015 5.1 One and two-point perspective In Chapter 5 we saw how to calculate the center of vision and the viewing distance for a square in one or two-point perspective.
Chapter 5 Drawing a cube Math 4520, Spring 2015 5.1 One and two-point perspective In Chapter 5 we saw how to calculate the center of vision and the viewing distance for a square in one or two-point perspective.
Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat?
 Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat? Notice that the distance from the bottom of the ladder
Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat? Notice that the distance from the bottom of the ladder
Lesson 4: Fundamental Theorem of Similarity (FTS)
 Student Outcomes Students experimentally verify the properties related to the Fundamental Theorem of Similarity (FTS). Lesson Notes The goal of this activity is to show students the properties of the Fundamental
Student Outcomes Students experimentally verify the properties related to the Fundamental Theorem of Similarity (FTS). Lesson Notes The goal of this activity is to show students the properties of the Fundamental
h r c On the ACT, remember that diagrams are usually drawn to scale, so you can always eyeball to determine measurements if you get stuck.
 ACT Plane Geometry Review Let s first take a look at the common formulas you need for the ACT. Then we ll review the rules for the tested shapes. There are also some practice problems at the end of this
ACT Plane Geometry Review Let s first take a look at the common formulas you need for the ACT. Then we ll review the rules for the tested shapes. There are also some practice problems at the end of this
Mathematics Success Level F
 T598 [OBJECTIVE] The student will find the perimeter and area of rectangles and triangles. [MATERIALS] Student pages S204 S212 Transparencies T612, T614, T616, T618, T620, T622 Ruler Scissors Gridded index
T598 [OBJECTIVE] The student will find the perimeter and area of rectangles and triangles. [MATERIALS] Student pages S204 S212 Transparencies T612, T614, T616, T618, T620, T622 Ruler Scissors Gridded index
SESSION ONE GEOMETRY WITH TANGRAMS AND PAPER
 SESSION ONE GEOMETRY WITH TANGRAMS AND PAPER Outcomes Develop confidence in working with geometrical shapes such as right triangles, squares, and parallelograms represented by concrete pieces made of cardboard,
SESSION ONE GEOMETRY WITH TANGRAMS AND PAPER Outcomes Develop confidence in working with geometrical shapes such as right triangles, squares, and parallelograms represented by concrete pieces made of cardboard,
3.3. You wouldn t think that grasshoppers could be dangerous. But they can damage
 Grasshoppers Everywhere! Area and Perimeter of Parallelograms on the Coordinate Plane. LEARNING GOALS In this lesson, you will: Determine the perimeter of parallelograms on a coordinate plane. Determine
Grasshoppers Everywhere! Area and Perimeter of Parallelograms on the Coordinate Plane. LEARNING GOALS In this lesson, you will: Determine the perimeter of parallelograms on a coordinate plane. Determine
2005 Fryer Contest. Solutions
 Canadian Mathematics Competition n activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Fryer Contest Wednesday, pril 20, 2005 Solutions c 2005
Canadian Mathematics Competition n activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2005 Fryer Contest Wednesday, pril 20, 2005 Solutions c 2005
Intermediate Mathematics League of Eastern Massachusetts
 Meet #5 April 2003 Intermediate Mathematics League of Eastern Massachusetts www.imlem.org Meet #5 April 2003 Category 1 Mystery You may use a calculator 1. In his book In an Average Lifetime, author Tom
Meet #5 April 2003 Intermediate Mathematics League of Eastern Massachusetts www.imlem.org Meet #5 April 2003 Category 1 Mystery You may use a calculator 1. In his book In an Average Lifetime, author Tom
B. Examples: 1. At NVHS, there are 104 teachers and 2204 students. What is the approximate teacher to student ratio?
 Name Date Period Notes Formal Geometry Chapter 7 Similar Polygons 7.1 Ratios and Proportions A. Definitions: 1. Ratio: 2. Proportion: 3. Cross Products Property: 4. Equivalent Proportions: B. Examples:
Name Date Period Notes Formal Geometry Chapter 7 Similar Polygons 7.1 Ratios and Proportions A. Definitions: 1. Ratio: 2. Proportion: 3. Cross Products Property: 4. Equivalent Proportions: B. Examples:
MAT 1160 Mathematics, A Human Endeavor
 MAT 1160 Mathematics, A Human Endeavor Syllabus: office hours, grading Schedule (note exam dates) Academic Integrity Guidelines Homework & Quizzes Course Web Site : www.eiu.edu/ mathcs/mat1160/ 2005 09,
MAT 1160 Mathematics, A Human Endeavor Syllabus: office hours, grading Schedule (note exam dates) Academic Integrity Guidelines Homework & Quizzes Course Web Site : www.eiu.edu/ mathcs/mat1160/ 2005 09,
Building Concepts: Ratios Within and Between Scaled Shapes
 Lesson Overview In this TI-Nspire lesson, students learn that ratios are connected to geometry in multiple ways. When one figure is an enlarged or reduced copy of another by some scale factor, the ratios
Lesson Overview In this TI-Nspire lesson, students learn that ratios are connected to geometry in multiple ways. When one figure is an enlarged or reduced copy of another by some scale factor, the ratios
Lesson 27: Sine and Cosine of Complementary and Special Angles
 Lesson 7 M Classwork Example 1 If α and β are the measurements of complementary angles, then we are going to show that sin α = cos β. In right triangle ABC, the measurement of acute angle A is denoted
Lesson 7 M Classwork Example 1 If α and β are the measurements of complementary angles, then we are going to show that sin α = cos β. In right triangle ABC, the measurement of acute angle A is denoted
Suppose that two squares are cut from opposite corners of a chessboard. Can the remaining squares be completely covered by 31 dominoes?
 Chapter 2 Parent Guide Reasoning in Geometry Reasoning is a thinking process that progresses logically from one idea to another. Logical reasoning advances toward a conclusion in such a way as to be understood
Chapter 2 Parent Guide Reasoning in Geometry Reasoning is a thinking process that progresses logically from one idea to another. Logical reasoning advances toward a conclusion in such a way as to be understood
UNIVERSITY OF NORTHERN COLORADO MATHEMATICS CONTEST
 UNIVERSITY OF NORTHERN COLORADO MATHEMATICS CONTEST First Round For all Colorado Students Grades 7-12 October 31, 2009 You have 90 minutes no calculators allowed The average of n numbers is their sum divided
UNIVERSITY OF NORTHERN COLORADO MATHEMATICS CONTEST First Round For all Colorado Students Grades 7-12 October 31, 2009 You have 90 minutes no calculators allowed The average of n numbers is their sum divided
5.1, 5.2, 5.3 Properites of Exponents last revised 12/28/2010
 48 5.1, 5.2, 5.3 Properites of Exponents last revised 12/28/2010 Properites of Exponents 1. *Simplify each of the following: a. b. 2. c. d. 3. e. 4. f. g. 5. h. i. j. Negative exponents are NOT considered
48 5.1, 5.2, 5.3 Properites of Exponents last revised 12/28/2010 Properites of Exponents 1. *Simplify each of the following: a. b. 2. c. d. 3. e. 4. f. g. 5. h. i. j. Negative exponents are NOT considered
ACT Coordinate Geometry Review
 ACT Coordinate Geometry Review Here is a brief review of the coordinate geometry concepts tested on the ACT. Note: there is no review of how to graph an equation on this worksheet. Questions testing this
ACT Coordinate Geometry Review Here is a brief review of the coordinate geometry concepts tested on the ACT. Note: there is no review of how to graph an equation on this worksheet. Questions testing this
Ch. 3 Parallel and Perpendicular Lines
 Ch. 3 Parallel and Perpendicular Lines Section 3.1 Lines and Angles 1. I CAN identify relationships between figures in space. 2. I CAN identify angles formed by two lines and a transversal. Key Vocabulary:
Ch. 3 Parallel and Perpendicular Lines Section 3.1 Lines and Angles 1. I CAN identify relationships between figures in space. 2. I CAN identify angles formed by two lines and a transversal. Key Vocabulary:
16.1 Segment Length and Midpoints
 Name lass ate 16.1 Segment Length and Midpoints Essential Question: How do you draw a segment and measure its length? Explore Exploring asic Geometric Terms In geometry, some of the names of figures and
Name lass ate 16.1 Segment Length and Midpoints Essential Question: How do you draw a segment and measure its length? Explore Exploring asic Geometric Terms In geometry, some of the names of figures and
Squares and Square Roots Algebra 11.1
 Squares and Square Roots Algebra 11.1 To square a number, multiply the number by itself. Practice: Solve. 1. 1. 0.6. (9) 4. 10 11 Squares and Square Roots are Inverse Operations. If =y then is a square
Squares and Square Roots Algebra 11.1 To square a number, multiply the number by itself. Practice: Solve. 1. 1. 0.6. (9) 4. 10 11 Squares and Square Roots are Inverse Operations. If =y then is a square
YEAR 8 Mathematics. Assessment 2: Pythagoras Theorem and Geometry
 Finds correct answer Finds correct answer YEAR 8 Mathematics Assessment : Pythagoras Theorem and Geometry Name: Class: DUE DATE: Thursday 9 th June (Week 10) MARK : Pythagoras (Ques 1-3): /13 ASSESSMENT
Finds correct answer Finds correct answer YEAR 8 Mathematics Assessment : Pythagoras Theorem and Geometry Name: Class: DUE DATE: Thursday 9 th June (Week 10) MARK : Pythagoras (Ques 1-3): /13 ASSESSMENT
Squares and Square Roots
 Squares and Square Roots Focus on After this lesson, you will be able to... determine the square of a whole number determine the square root of a perfect square Literacy Link A square number is the product
Squares and Square Roots Focus on After this lesson, you will be able to... determine the square of a whole number determine the square root of a perfect square Literacy Link A square number is the product
Lesson Idea by: Van McPhail, Okanagan Mission Secondary
 Click to Print This Page Fit by Design or Design to Fit Mechanical Drafter Designer Lesson Idea by: Van McPhail, Okanagan Mission Secondary There's hardly any object in your home or school that hasn't
Click to Print This Page Fit by Design or Design to Fit Mechanical Drafter Designer Lesson Idea by: Van McPhail, Okanagan Mission Secondary There's hardly any object in your home or school that hasn't
Mathematics Background
 For a more robust teacher experience, please visit Teacher Place at mathdashboard.com/cmp3 The Measurement Process While this Unit does not focus on the global aspects of what it means to measure, it does
For a more robust teacher experience, please visit Teacher Place at mathdashboard.com/cmp3 The Measurement Process While this Unit does not focus on the global aspects of what it means to measure, it does
Name Date MASCOT PAINTING. Use the picture on the left and enlarge it by using the grid below. II Classroom Strategies Blackline Master
 MASCOT PAINTING Use the picture on the left and enlarge it by using the grid below. Page 206 Classroom Strategies Blackline Master II - 64 Draw Me in 3-D Use cubes to construct the building described in
MASCOT PAINTING Use the picture on the left and enlarge it by using the grid below. Page 206 Classroom Strategies Blackline Master II - 64 Draw Me in 3-D Use cubes to construct the building described in
Georgia Tech HSMC 2010
 Georgia Tech HSMC 2010 Junior Varsity Multiple Choice February 27 th, 2010 1. A box contains nine balls, labeled 1, 2,,..., 9. Suppose four balls are drawn simultaneously. What is the probability that
Georgia Tech HSMC 2010 Junior Varsity Multiple Choice February 27 th, 2010 1. A box contains nine balls, labeled 1, 2,,..., 9. Suppose four balls are drawn simultaneously. What is the probability that
Part I Multiple Choice
 Oregon Focus on Lines and Angles Block 3 Practice Test ~ The Pythagorean Theorem Name Period Date Long/Short Term Learning Targets MA.MS.08.ALT.05: I can understand and apply the Pythagorean Theorem. MA.MS.08.AST.05.1:
Oregon Focus on Lines and Angles Block 3 Practice Test ~ The Pythagorean Theorem Name Period Date Long/Short Term Learning Targets MA.MS.08.ALT.05: I can understand and apply the Pythagorean Theorem. MA.MS.08.AST.05.1:
5.3. Area of Polygons and Circles Play Area. My Notes ACTIVITY
 Area of Polygons and Circles SUGGESTED LEARNING STRATEGIES: Think/Pair/Share ACTIVITY 5.3 Pictured below is an aerial view of a playground. An aerial view is the view from above something. Decide what
Area of Polygons and Circles SUGGESTED LEARNING STRATEGIES: Think/Pair/Share ACTIVITY 5.3 Pictured below is an aerial view of a playground. An aerial view is the view from above something. Decide what
Orange High School. Year 8 Mathematics. Assignment 1
 Full name: Teacher: Due date: Orange High School Year 8 Mathematics Assignment 1 2017 Syllabus Outcomes This assignment will address many outcomes from the Stage 4 syllabus, with particular focus on: Calculates
Full name: Teacher: Due date: Orange High School Year 8 Mathematics Assignment 1 2017 Syllabus Outcomes This assignment will address many outcomes from the Stage 4 syllabus, with particular focus on: Calculates
A natural number is called a perfect cube if it is the cube of some. some natural number.
 A natural number is called a perfect square if it is the square of some natural number. i.e., if m = n 2, then m is a perfect square where m and n are natural numbers. A natural number is called a perfect
A natural number is called a perfect square if it is the square of some natural number. i.e., if m = n 2, then m is a perfect square where m and n are natural numbers. A natural number is called a perfect
HANDS-ON TRANSFORMATIONS: DILATIONS AND SIMILARITY (Poll Code 44273)
 HANDS-ON TRANSFORMATIONS: DILATIONS AND SIMILARITY (Poll Code 44273) Presented by Shelley Kriegler President, Center for Mathematics and Teaching shelley@mathandteaching.org Fall 2014 8.F.1 8.G.3 8.G.4
HANDS-ON TRANSFORMATIONS: DILATIONS AND SIMILARITY (Poll Code 44273) Presented by Shelley Kriegler President, Center for Mathematics and Teaching shelley@mathandteaching.org Fall 2014 8.F.1 8.G.3 8.G.4
