Catty Corner. Side Lengths in Two and. Three Dimensions
|
|
|
- Neil Charles
- 5 years ago
- Views:
Transcription
1 Catty Corner Side Lengths in Two and 4 Three Dimensions WARM UP A 1. Imagine that the rectangular solid is a room. An ant is on the floor situated at point A. Describe the shortest path the ant can crawl to get to point B in the corner of the ceiling. 2. Suppose it isn t really an ant at all it s a fly! Describe the shortest path the fly can fly to get from point A to point B. 3. If the ant s path and the fly s path were connected, what figure would they form? B LEARNING GOALS Apply the Pythagorean Theorem to determine unknown side lengths of right triangles in mathematical and real-world problems. Apply the Pythagorean Theorem to determine the lengths of diagonals of two- and three-dimensional figures. KEY TERM diagonal You have learned about the Pythagorean Theorem and its converse. How can you apply the Pythagorean Theorem to determine lengths in geometric figures? LESSON 4: Catty Corner M4-99 C03_SE_M04_T02_L04.indd 99
2 Getting Started Diagonally Draw all of the sides you cannot see in each rectangular solid using dotted lines. Then draw a three-dimensional diagonal using a solid line. 1. How many threedimensional diagonals can be drawn in each figure? 2. M4-100 TOPIC 2: Pythagorean Theorem C03_SE_M04_T02_L04.indd 100
3 ACTIVITY 4.1 Determining the Lengths of Diagonals of Rectangles and Trapezoids Previously, you have drawn or created many right triangles and used the Pythagorean Theorem to determine side lengths. In this lesson, you will explore the diagonals of various shapes. 1. Rectangle ABCD is shown. A B 8 ft D 15 ft a. Draw diagonal AC in Rectangle ABCD. Then, determine the length of diagonal AC. C Be on the lookout for right triangles. b. Draw diagonal BD in Rectangle ABCD. Then, determine the length of diagonal BD. c. What can you conclude about the diagonals of this rectangle? LESSON 4: Catty Corner M4-101 C03_SE_M04_T02_L04.indd 101
4 2. Square ABCD is shown. A B 10 m D C a. Draw diagonal AC in Square ABCD. Then, determine the length of diagonal AC. b. Draw diagonal BD in Square ABCD. Then, determine the length of diagonal BD. All squares are also rectangles, so does your conclusion make sense? c. What can you conclude about the diagonals of this square? M4-102 TOPIC 2: Pythagorean Theorem C03_SE_M04_T02_L04.indd 102
5 3. Graph and label the coordinates of the vertices of Trapezoid ABCD: A (1, 2), B (7, 2), C (7, 5), D (3, 5). 10 y NOTES x a. Draw diagonal AC in Trapezoid ABCD. b. What right triangle can be used to determine the length of diagonal AC? c. Determine the length of diagonal AC. d. Draw diagonal BD in Trapezoid ABCD. e. What right triangle can be used to determine the length of diagonal BD? f. Determine the length of diagonal BD. g. What can you conclude about the diagonals of this trapezoid? LESSON 4: Catty Corner M4-103 C03_SE_M04_T02_L04.indd 103
6 4. Graph and label the coordinates of the vertices of isosceles Trapezoid ABCD: A (1, 2), B (9, 2), C (7, 5), D (3, 5). 10 y How is this trapezoid different from the first trapezoid you drew? a. Draw diagonal AC in Trapezoid ABCD x b. What right triangle can be used to determine the length of diagonal AC? M4-104 TOPIC 2: Pythagorean Theorem C03_SE_M04_T02_L04.indd 104
7 c. Determine the length of diagonal AC. d. Draw diagonal BD in Trapezoid ABCD. What is your prediction about the diagonals of this isosceles trapezoid e. What right triangle can be used to determine the length of diagonal BD? f. Determine the length of diagonal BD. g. What can you conclude about the diagonals of this isosceles trapezoid? LESSON 4: Catty Corner M4-105 C03_SE_M04_T02_L04.indd 105
8 ACTIVITY 4.2 Using Diagonals to Solve Problems Use your knowledge of right triangles, the Pythagorean Theorem, and area formulas. 1. Determine the area of each shaded region. Use 3.14 for p and round to the nearest tenth. a. A rectangle is inscribed in a circle as shown. 6 cm 10 cm b. The figure is composed of a right triangle and a semi-circle. 8 mm 5 mm M4-106 TOPIC 2: Pythagorean Theorem C03_SE_M04_T02_L04.indd 106
9 ACTIVITY 4.3 Diagonals in Solid Figures A rectangular box of long-stem roses is 18 inches in length, 6 inches in width, and 4 inches in height. Without bending a long-stem rose, you are to determine the maximum length of a rose that will fit into the box. 1. What makes this problem different from all of the previous applications of the Pythagorean Theorem? 2. Compare a two-dimensional diagonal to a three-dimensional diagonal. Describe the similarities and differences. 2-D Diagonal 3-D Diagonal 3. Which diagonal represents the maximum length of a rose that can fit into a box? LESSON 4: Catty Corner M4-107 C03_SE_M04_T02_L04.indd 107
10 4. Consider the rectangular solid shown. a. Draw all of the sides in the rectangular solid you cannot see using dotted lines. 18 in. 6 in. 4 in. b. Draw a three-dimensional diagonal in the rectangular solid. c. Let s consider that the three-dimensional diagonal you drew in the rectangular solid is also the hypotenuse of a right triangle. If a vertical edge is one of the legs of that right triangle, where is the second leg of that same right triangle? d. Draw the second leg using a dotted line. Then lightly shade the right triangle. e. Determine the length of the second leg you drew. f. Determine the length of the three-dimensional diagonal. g. What does the length of the three-dimensional diagonal represent in terms of this problem situation? 5. Describe how the Pythagorean Theorem was used to solve this problem. M4-108 TOPIC 2: Pythagorean Theorem C03_SE_M04_T02_L04.indd 108
11 ACTIVITY 4.4 Practice with Three- Dimensional Diagonals Determine the length of the diagonal of each rectangular solid in. 4 m 8 m 7 m 6 in. 4 in cm 7 yd 6 cm 5 yd 7 yd 10 cm in. 12 ft 3 in. 15 in. 2 ft 2 ft LESSON 4: Catty Corner M4-109 C03_SE_M04_T02_L04.indd 109
12 NOTES TALK the TALK The Ant and the Fly Again A rectangular room is 10 ft 3 16 ft 3 8 ft. An ant crawls from point A to point B taking the shortest path. A fly flies from point A to point B taking the shortest path. B 8 feet 10 feet A 16 feet 1. Whose path was shorter? 2. How much shorter is the shorter path? M4-110 TOPIC 2: Pythagorean Theorem C03_SE_M04_T02_L04.indd 110
Lesson 6.1 Skills Practice
Lesson 6.1 Skills Practice Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Vocabulary Match each definition to its corresponding term. 1. A mathematical statement
Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions.
Student Outcomes Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions. Lesson Notes It is recommended that students have access to a calculator as they work
UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet
Name Period Date UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet 24.1 The Pythagorean Theorem Explore the Pythagorean theorem numerically, algebraically, and geometrically. Understand a proof
6.1 Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Can That Be Right? 6.3 Pythagoras to the Rescue
Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
Lesson 1 Area of Parallelograms
NAME DATE PERIOD Lesson 1 Area of Parallelograms Words Formula The area A of a parallelogram is the product of any b and its h. Model Step 1: Write the Step 2: Replace letters with information from picture
Square Roots and the Pythagorean Theorem
UNIT 1 Square Roots and the Pythagorean Theorem Just for Fun What Do You Notice? Follow the steps. An example is given. Example 1. Pick a 4-digit number with different digits. 3078 2. Find the greatest
Representing Square Numbers. Use materials to represent square numbers. A. Calculate the number of counters in this square array.
1.1 Student book page 4 Representing Square Numbers You will need counters a calculator Use materials to represent square numbers. A. Calculate the number of counters in this square array. 5 5 25 number
Lesson 3 Pre-Visit Perimeter and Area
Lesson 3 Pre-Visit Perimeter and Area Objective: Students will be able to: Distinguish between area and perimeter. Calculate the perimeter of a polygon whose side lengths are given or can be determined.
The Pythagorean Theorem 8.6.C
? LESSON 8.1 The Pythagorean Theorem ESSENTIAL QUESTION Expressions, equations, and relationships 8.6.C Use models and diagrams to explain the Pythagorean Theorem. 8.7.C Use the Pythagorean Theorem...
AREA See the Math Notes box in Lesson for more information about area.
AREA..1.. After measuring various angles, students look at measurement in more familiar situations, those of length and area on a flat surface. Students develop methods and formulas for calculating the
1. Convert 60 mi per hour into km per sec. 2. Convert 3000 square inches into square yards.
ACT Practice Name Geo Unit 3 Review Hour Date Topics: Unit Conversions Length and Area Compound shapes Removing Area Area and Perimeter with radicals Isosceles and Equilateral triangles Pythagorean Theorem
Student Instruction Sheet: Unit 4 Lesson 1. Pythagorean Theorem
Student Instruction Sheet: Unit 4 Lesson 1 Suggested time: 75 minutes Pythagorean Theorem What s important in this lesson: In this lesson you will learn the Pythagorean Theorem and how to apply the theorem
Squares and Square Roots Algebra 11.1
Squares and Square Roots Algebra 11.1 To square a number, multiply the number by itself. Practice: Solve. 1. 1. 0.6. (9) 4. 10 11 Squares and Square Roots are Inverse Operations. If =y then is a square
G.MG.A.3: Area of Polygons
Regents Exam Questions G.MG.A.3: Area of Polygons www.jmap.org Name: G.MG.A.3: Area of Polygons If the base of a triangle is represented by x + 4 and the height is represented by x, which expression represents
April 09, areas of parallelograms and triangles 2016 ink.notebook. Page 126. Page 128. Page Area of Parallelograms and Triangles
11.1 areas of parallelograms and triangles 2016 ink.noteook Page 126 Page 128 Page 127 11.1 Area of Parallelograms and Triangles Lesson Ojectives Standards Lesson Notes Page 129 11.1 Areas of Parallelograms
Cross Sections of Three-Dimensional Figures
Domain 4 Lesson 22 Cross Sections of Three-Dimensional Figures Common Core Standard: 7.G.3 Getting the Idea A three-dimensional figure (also called a solid figure) has length, width, and height. It is
How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr.
Common Core Standard: 8.G.6, 8.G.7 How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.2 What Is Special
Page 1 part 1 PART 2
Page 1 part 1 PART 2 Page 2 Part 1 Part 2 Page 3 part 1 Part 2 Page 4 Page 5 Part 1 10. Which point on the curve y x 2 1 is closest to the point 4,1 11. The point P lies in the first quadrant on the graph
Similar Figures 2.5. ACTIVITY: Reducing Photographs. How can you use proportions to help make decisions in art, design, and magazine layouts?
.5 Similar Figures How can you use proportions to help make decisions in art, design, and magazine layouts? In a computer art program, when you click and drag on a side of a photograph, you distort it.
Geometry. Warm Ups. Chapter 11
Geometry Warm Ups Chapter 11 Name Period Teacher 1 1.) Find h. Show all work. (Hint: Remember special right triangles.) a.) b.) c.) 2.) Triangle RST is a right triangle. Find the measure of angle R. Show
3.3. You wouldn t think that grasshoppers could be dangerous. But they can damage
Grasshoppers Everywhere! Area and Perimeter of Parallelograms on the Coordinate Plane. LEARNING GOALS In this lesson, you will: Determine the perimeter of parallelograms on a coordinate plane. Determine
All About That Base... and Height
All About That Base... and Height Area of Triangles and Quadrilaterals 2 WARM UP Write 3 different expressions to describe the total area of this rectangle. LEARNING GOALS State and compare the attributes
Whirlygigs for Sale! Rotating Two-Dimensional Figures through Space. LESSON 4.1 Skills Practice. Vocabulary. Problem Set
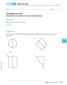LESSON.1 Skills Practice Name Date Whirlygigs for Sale! Rotating Two-Dimensional Figures through Space Vocabulary Describe the term in your own words. 1. disc Problem Set Write the name of the solid figure
The Pythagorean Theorem
. The Pythagorean Theorem Goals Draw squares on the legs of the triangle. Deduce the Pythagorean Theorem through exploration Use the Pythagorean Theorem to find unknown side lengths of right triangles
Lesson 8.3: Scale Diagrams, page 479
c) e.g., One factor is that the longer the distance, the less likely to maintain a high constant speed throughout due to fatigue. By the end of the race the speed will usually be lower than at the start.
Pythagorean Theorem. 2.1 Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem... 45
Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
3.9. Pythagorean Theorem Stop the Presses. My Notes ACTIVITY
Pythagorean Theorem SUGGESTED LEARNING STRATEGIES: Marking the Text, Predict and Confirm, Shared Reading Jayla and Sidney are co-editors-in-chief of the school yearbook. They have just finished the final
Area of Composite Figures. ESSENTIAL QUESTION do you find the area of composite figures? 7.9.C
? LESSON 9.4 Area of Composite Figures ESSENTIAL QUESTION How do you find the area of composite figures? Equations, expressions, and relationships Determine the area of composite figures containing combinations
MATH MEASUREMENT AND GEOMETRY
Students: 1. Students choose appropriate units of measure and use ratios to convert within and between measurement systems to solve problems. 1. Compare weights, capacities, geometric measures, time, and
FSA Geometry EOC Getting ready for. Circles, Geometric Measurement, and Geometric Properties with Equations.
Getting ready for. FSA Geometry EOC Circles, Geometric Measurement, and Geometric Properties with Equations 2014-2015 Teacher Packet Shared by Miami-Dade Schools Shared by Miami-Dade Schools MAFS.912.G-C.1.1
Part I Multiple Choice
Oregon Focus on Lines and Angles Block 3 Practice Test ~ The Pythagorean Theorem Name Period Date Long/Short Term Learning Targets MA.MS.08.ALT.05: I can understand and apply the Pythagorean Theorem. MA.MS.08.AST.05.1:
6.00 Trigonometry Geometry/Circles Basics for the ACT. Name Period Date
6.00 Trigonometry Geometry/Circles Basics for the ACT Name Period Date Perimeter and Area of Triangles and Rectangles The perimeter is the continuous line forming the boundary of a closed geometric figure.
E G 2 3. MATH 1012 Section 8.1 Basic Geometric Terms Bland
MATH 1012 Section 8.1 Basic Geometric Terms Bland Point A point is a location in space. It has no length or width. A point is represented by a dot and is named by writing a capital letter next to the dot.
Geometry 2001 part 1
Geometry 2001 part 1 1. Point is the center of a circle with a radius of 20 inches. square is drawn with two vertices on the circle and a side containing. What is the area of the square in square inches?
2016 Summer Break Packet for Students Entering Geometry Common Core
2016 Summer Break Packet for Students Entering Geometry Common Core Name: Note to the Student: In middle school, you worked with a variety of geometric measures, such as: length, area, volume, angle, surface
Lesson 20T ~ Parts of Circles
Lesson 20T ~ Parts of Circles Name Period Date 1. Draw a diameter. 2. Draw a chord. 3. Draw a central angle. 4. Draw a radius. 5. Give two names for the line drawn in the circle. Given the radius, find
#2. Rhombus ABCD has an area of 464 square units. If DB = 18 units, find AC. #3. What is the area of the shaded sector if the measure of <ABC is 80?
1 Pre-AP Geometry Chapter 12 Test Review Standards/Goals: F.1.a.: I can find the perimeter and area of common plane figures, such as: triangles, quadrilaterals, regular polygons, and irregular figures,
Paper Folding: Maximizing the Area of a Triangle Algebra 2
Paper Folding: Maximizing the Area of a Triangle Algebra (This lesson was developed by Jan Baysden of Hoggard High School and Julie Fonvielle of Whiteville High School during the Leading to Success in
Fair Game Review. Chapter 4. Name Date. Find the area of the square or rectangle Find the area of the patio.
Name Date Chapter Fair Game Review Find the area of the square or rectangle... ft cm 0 ft cm.. in. d in. d. Find the area of the patio. ft 0 ft Copright Big Ideas Learning, LLC Big Ideas Math Green Name
The Pythagorean Theorem is used in many careers on a regular basis. Construction
Applying the Pythagorean Theorem Lesson 2.5 The Pythagorean Theorem is used in many careers on a regular basis. Construction workers and cabinet makers use the Pythagorean Theorem to determine lengths
Geometry Final Exam Review 2012 #
1 PART 1: Multiple Choice (40 x 2 points = 80%). PART 2: Open Ended (2 x 10 = 20%) 1) Find the volume and surface area of the following rectangular prisms 2) Find the surface area of the following cylinders.
Set 6: Understanding the Pythagorean Theorem Instruction
Instruction Goal: To provide opportunities for students to develop concepts and skills related to understanding that the Pythagorean theorem is a statement about areas of squares on the sides of a right
10.3 Areas of Similar Polygons
10.3 Areas of Similar Polygons Learning Objectives Understand the relationship between the scale factor of similar polygons and their areas. Apply scale factors to solve problems about areas of similar
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 17, :30 to 3:30 p.m.
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 17, 2017 12:30 to 3:30 p.m., only Student Name: School Name: The possession or use of any communications
Areas of Tropezoids, Rhombuses, and Kites
102 Areas of Tropezoids, Rhombuses, and Kites MathemaHcs Florida Standards MAFS.912.G-MG.1.1 Use geometric shapes, their measures, and their properties to describe objects. MP1. MP3, MP 4,MP6 Objective
The area A of a trapezoid is one half the product of the height h and the sum of the lengths of its bases, b 1 and b 2.
ALGEBRA Find each missing length. 21. A trapezoid has a height of 8 meters, a base length of 12 meters, and an area of 64 square meters. What is the length of the other base? The area A of a trapezoid
11.2 Areas of Trapezoids,
11. Areas of Trapezoids, Rhombuses, and Kites Goal p Find areas of other types of quadrilaterals. Your Notes VOCABULARY Height of a trapezoid THEOREM 11.4: AREA OF A TRAPEZOID b 1 The area of a trapezoid
University of Houston High School Mathematics Contest Geometry Exam Spring 2016
University of Houston High School Mathematics ontest Geometry Exam Spring 016 nswer the following. Note that diagrams may not be drawn to scale. 1. In the figure below, E, =, = 4 and E = 0. Find the length
h r c On the ACT, remember that diagrams are usually drawn to scale, so you can always eyeball to determine measurements if you get stuck.
ACT Plane Geometry Review Let s first take a look at the common formulas you need for the ACT. Then we ll review the rules for the tested shapes. There are also some practice problems at the end of this
Learning Log Title: CHAPTER 2: ARITHMETIC STRATEGIES AND AREA. Date: Lesson: Chapter 2: Arithmetic Strategies and Area
Chapter 2: Arithmetic Strategies and Area CHAPTER 2: ARITHMETIC STRATEGIES AND AREA Date: Lesson: Learning Log Title: Date: Lesson: Learning Log Title: Chapter 2: Arithmetic Strategies and Area Date: Lesson:
Area of Composite Figures. ESSENTIAL QUESTION How do you find the area of composite figures? 7.G.2.6
LESSON 9.3 Area of Composite Figures Solve real-world and mathematical problems involving area, of objects composed of triangles, quadrilaterals, polygons,. ESSENTIAL QUESTION How do you find the area
ML # 1: Similar Figures and Scale Drawings (Unit 7 Math 7 PLUS) SCALE FACTOR: SIMILAR FIGURES:
ML # 1: Similar Figures and Scale Drawings (Unit 7 Math 7 PLUS) SCALE FACTOR: SIMILAR FIGURES: Corresponding Sides and Angles Corresponding Sides and Angles: Sides or angles that lie in the same location
MEA 501 LESSON _NOTES Period. CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must MEA 301 Compute the perimeter of polygons when all
MEA 501 LESSON _NOTES Period Name CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must MEA 301 Compute the perimeter of polygons when all attain mastery at this level side lengths are given MEA 302 Compute
You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion)
Pre-Test Unit 7: Pythagorean Theorem KEY You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion) 1. What is the IF-THEN statement for the Pythagorean Theorem?
June 2016 Regents GEOMETRY COMMON CORE
1 A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation? 4) 2
Lesson 1 Pre-Visit Ballpark Figures Part 1
Lesson 1 Pre-Visit Ballpark Figures Part 1 Objective: Students will be able to: Estimate, measure, and calculate length, perimeter, and area of various rectangles. Time Requirement: 1 class period, longer
Lesson: Pythagorean Theorem Lesson Topic: Use Pythagorean theorem to calculate the hypotenuse
Lesson: Pythagorean Theorem Lesson Topic: Use Pythagorean theorem to calculate the hypotenuse Question 1: What is the length of the hypotenuse? ft Question 2: What is the length of the hypotenuse? m Question
Grade 3, Module 4: Multiplication and Area
Grade 3, Module 4: Multiplication and Area Mission: Find the Area Topic A: Foundations for Understanding Area In Topic A, students begin to conceptualize area as the amount of two- dimensional surface
Problem of the Month: Between the Lines
Problem of the Month: Between the Lines The Problems of the Month (POM) are used in a variety of ways to promote problem solving and to foster the first standard of mathematical practice from the Common
Topic 1 Pythagorean Theorem
Topic 1 Pythagorean Theorem Question 1 name Perimeter of a trapezoid text In trapezoid ABCD the sides AB and CD are equal. The lengths of BC and AD are b 1 = $x and b 2 = $y respectively. The height of
Foundations of Math 11: Unit 2 Proportions. The scale factor can be written as a ratio, fraction, decimal, or percentage
Lesson 2.3 Scale Name: Definitions 1) Scale: 2) Scale Factor: The scale factor can be written as a ratio, fraction, decimal, or percentage Formula: Formula: Example #1: A small electronic part measures
Problem of the Month: Between the Lines
Problem of the Month: Between the Lines Overview: In the Problem of the Month Between the Lines, students use polygons to solve problems involving area. The mathematical topics that underlie this POM are
AREA AND PERIMETER RECTANGLE WORKSHEETS ARCHIVE
29 April, 2018 AREA AND PERIMETER RECTANGLE WORKSHEETS ARCHIVE Document Filetype: PDF 443.87 KB 0 AREA AND PERIMETER RECTANGLE WORKSHEETS ARCHIVE Download free printable worksheets on Finding Perimeter
Concept: Pythagorean Theorem Name:
Concept: Pythagorean Theorem Name: Interesting Fact: The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations. This famous theorem is named for the Greek mathematician and
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem I. Lesson Objectives: -Students will be able to recall definitions of angles, how to measure angles, and measurement systems
5.3. Area of Polygons and Circles Play Area. My Notes ACTIVITY
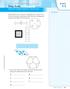Area of Polygons and Circles SUGGESTED LEARNING STRATEGIES: Think/Pair/Share ACTIVITY 5.3 Pictured below is an aerial view of a playground. An aerial view is the view from above something. Decide what
Meet #5 March Intermediate Mathematics League of Eastern Massachusetts
Meet #5 March 2008 Intermediate Mathematics League of Eastern Massachusetts Meet #5 March 2008 Category 1 Mystery 1. In the diagram to the right, each nonoverlapping section of the large rectangle is
QaD Teacher Support Materials
QaD Teacher Support Materials Focus: Develop skills at interpreting geometric diagrams and using them to solve problems. Instructions Remember to download the Weekly Class Report and use it to help plan
Analytic Geometry EOC Study Booklet Geometry Domain Units 1-3 & 6
DOE Assessment Guide Questions (2015) Analytic Geometry EOC Study Booklet Geometry Domain Units 1-3 & 6 Question Example Item #1 Which transformation of ΔMNO results in a congruent triangle? Answer Example
Geometry. Practice Pack
Geometry Practice Pack WALCH PUBLISHING Table of Contents Unit 1: Lines and Angles Practice 1.1 What Is Geometry?........................ 1 Practice 1.2 What Is Geometry?........................ 2 Practice
7.3B STUDENT ACTIVITY #1
E MAT I CS 7.3B STUDENT ACTIVITY #1 PROBLEM: Right triangles MNP and DEF are similar. Find the length in inches of side EF. D M 6 in. P 9 in. N 24 in. F x E Since the triangles are similar, their corresponding
Name Date. Chapter 15 Final Review
Name Date Chapter 15 Final Review Tell whether the events are independent or dependent. Explain. 9) You spin a spinner twice. First Spin: You spin a 2. Second Spin: You spin an odd number. 10) Your committee
WS Stilwell Practice 11-1
Name: Date: Period: WS Stilwell Practice 11-1 Find the area of each figure. Show your formula, work, and answer. Be sure to label! 1) 2) A calculator is allowed 3) 4) 5) 6) 7) Rectangle: 8) Parallelogram:
Assignment 5 unit3-4-radicals. Due: Friday January 13 BEFORE HOMEROOM
Assignment 5 unit3-4-radicals Name: Due: Friday January 13 BEFORE HOMEROOM Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Write the prime factorization
Perimeters of Composite Figures
8. Perimeters of Composite Figures How can you find the perimeter of a composite figure? ACTIVITY: Finding a Pattern Work with a partner. Describe the pattern of the perimeters. Use your pattern to find
GAP CLOSING. Powers and Roots. Intermediate / Senior Student Book GAP CLOSING. Powers and Roots. Intermediate / Senior Student Book
GAP CLOSING Powers and Roots GAP CLOSING Powers and Roots Intermediate / Senior Student Book Intermediate / Senior Student Book Powers and Roots Diagnostic...3 Perfect Squares and Square Roots...6 Powers...
Grade 7 Mathematics Item Specifications Florida Standards Assessments
Assessment Limit MAFS7.G.1 Draw, construct, and describe geometrical figures and describe the relationships between them. MAFS.7.G.1.1 Solve problems involving scale drawings of geometric figures, including
18.2 Geometric Probability
Name Class Date 18.2 Geometric Probability Essential Question: What is geometric probability? Explore G.13.B Determine probabilities based on area to solve contextual problems. Using Geometric Probability
Date: Period: Quadrilateral Word Problems: Review Sheet
Name: Quadrilateral Word Problems: Review Sheet Date: Period: Geometry Honors Directions: Please answer the following on a separate sheet of paper. Completing this review sheet will help you to do well
Concept: Pythagorean Theorem Name:
Concept: Pythagorean Theorem Name: Interesting Fact: The Pythagorean Theorem was one of the earliest theorems known to ancient civilizations. This famous theorem is named for the Greek mathematician and
Lesson 17: Slicing a Right Rectangular Pyramid with a Plane
NYS COMMON COR MATHMATICS CURRICULUM Lesson 17 7 6 Student Outcomes Students describe polygonal regions that result from slicing a right rectangular pyramid by a plane perpendicular to the base and by
Find the area and perimeter of each figure. Round to the nearest tenth if necessary.
Find the area and perimeter of each figure. Round to the nearest tenth if necessary. 1. Use the Pythagorean Theorem to find the height h, of the parallelogram. Each pair of opposite sides of a parallelogram
Daily Warmup. - x 2 + x x 2 + x Questions from HW?? (7x - 39) (3x + 17) 1. BD bisects ABC. Find the m ABC.
Daily Warmup Questions from HW?? B 1. BD bisects ABC. Find the m ABC. (3x + 17) (7x - 39) C 2. The figure below is a regular polygon. Find the value of x. - x 2 + x + 43 A D 4x 2 + x - 37 3. The measure
The Pythagorean Theorem
6 6 What You ll Learn You ll learn to use the and its converse. Wh It s Important Carpentr Carpenters use the to determine the length of roof rafters when the frame a house. See Eample 3. The The stamp
Assignment Assignment for Lesson 3.1
Assignment Assignment for Lesson.1 Name Date Weaving a Rug Area and Perimeter of Rectangles and Squares 1. An artist is weaving a rectangular rug to match the pattern shown in the figure. Use the figure
The Grade 6 Common Core State Standards for Geometry specify that students should
The focus for students in geometry at this level is reasoning about area, surface area, and volume. Students also learn to work with visual tools for representing shapes, such as graphs in the coordinate
1 Version 2.0. Related Below-Grade and Above-Grade Standards for Purposes of Planning for Vertical Scaling:
Claim 1: Concepts and Procedures Students can explain and apply mathematical concepts and carry out mathematical procedures with precision and fluency. Content Domain: Geometry Target E [a]: Draw, construct,
The Pythagorean Theorem and Right Triangles
The Pythagorean Theorem and Right Triangles Student Probe Triangle ABC is a right triangle, with right angle C. If the length of and the length of, find the length of. Answer: the length of, since and
Seventh Grade Middle School Mathematics Contest
Seventh Grade Middle School Mathematics Contest 2002. Which of the following must be true about an obtuse triangle? a. All its interior angles are obtuse. b. It has two acute angles. c. It has exactly
IM 8 Ch Does It Always Work. Common Core Standard: Is the triangle a right triangle? Who is Pythagoras? CPM Materials modified by Mr.
Common Core Standard: 8.G.6 Is the triangle a right triangle? Who is Pythagoras? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.7 Does It Always Work? Date: Learning Target By the end of the period,
WVDE Math 7 G Solve Real-life and Mathematical Problems involving Angle Measure, Area, Surface Area, and Volume Test
WVDE Math 7 G Solve Real-life and Mathematical Problems involving Angle Measure, Area, Surface Area, and Volume Test 1 General Offline Instructions: Read each question carefully and decide which answer
is formed where the diameters intersect? Label the center.
E 26 Get Into Shape Hints or notes: A circle will be folded into a variety of geometric shapes. This activity provides the opportunity to assess the concepts, vocabulary and knowledge of relationships
2016 Geometry Honors Summer Packet
Name: 2016 Geometry Honors Summer Packet This packet is due the first day of school. It will be graded for completion and effort shown. There will be an assessment on these concepts the first week of school.
3 Kevin s work for deriving the equation of a circle is shown below.
June 2016 1. A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation?
Name. Ms. Nong. Due on: Per: Geometry 2 nd semester Math packet # 2 Standards: 8.0 and 16.0
Name FRIDAY, FEBRUARY 24 Due on: Per: TH Geometry 2 nd semester Math packet # 2 Standards: 8.0 and 16.0 8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume
Name Period No. Geometry Unit Review with Application Problems
Name Period No. Geometry Unit Review with Application Problems For problems 1-3, find the area of each figure. Show all steps. 1) 2) 4) Draw a parallelogram with an area of 50 sq. units in the 3) coordinate
GAP CLOSING. Powers and Roots. Intermediate / Senior Facilitator Guide
GAP CLOSING Powers and Roots Intermediate / Senior Facilitator Guide Powers and Roots Diagnostic...5 Administer the diagnostic...5 Using diagnostic results to personalize interventions...5 Solutions...5
CONSTRUCTION / HOUSING
CONSTRUCTION / HOUSING - PRINCE EDWARD ISLAND APPLIED MATHEMATICS 80A Table of Contents Construction/ Housing Reading a Tape Measure (Imperial)... - Using a Carpenter s Square... -5 Checking for Squareness
Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat?
Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat? Notice that the distance from the bottom of the ladder
GA Benchmark 8th Math (2008GABench8thMathset1)
Name: Date: 1. Tess will toss a fair coin 3 times. The possible results are illustrated in the tree diagram below. Based on the information given in the tree diagram, in how many ways (outcomes) can Tess