Limits and Continuity
|
|
|
- Estella Knight
- 6 years ago
- Views:
Transcription
1 Limits and Continuity February 26, 205 Previously, you learned about the concept of the it of a function, and an associated concept, continuity. These concepts can be generalised to functions of several variables. As always, we will discuss only the the case of functions of 2 variables, but the concepts are more or less the same for functions of more variables. Limits To discuss its, let s recall how they worked for single variables. function f(x), the expression For a f(x) = c means that if we choose numbers for x that gradually get closer and closer to a, then the values of f(x) will gradually get closer and closer to c. If you recall, there is a slight technical issue: the values of f(x) have to approach c regardless of whether the numbers you substitute for x are greater than or less than a. We expressed this by saying that if f(x) = c + and if then we say f(x) = c, f(x) = c.
2 The idea is that no matter how you get to a while walking along x, f(x) has to approach c. For functions of two variables, we use the same idea for its. Suppose now that you have a function f(x, y). We say that the it of f(x, y) as (x, y) approaches (a, b) means that as x approaches a and y approaches b, the value of f(x, y) will gradually approach c. Note that there are many ways that x can approach a while y simultaneously approaches b, as is shown in the following picture. As before, it doesn t matter how you get to (a, b). The important thing is that no matter which way you choose to get there, when you substitute the values (x, y) into f(x, y), the value of f(x, y) gets closer and closer to c. This should leave you with a question: how exactly do you compute the its? For just one path in the diagram above, you would need to check an infinite number of values of (x, y). Add to that the fact that there are an infinite number of paths, and you would have an unbelievably large quantity of numbers (x, y) to plug into f(x, y) to figure out the it. So how does one actually do it? 2 Continuity Thinking back to the case of single variable functions, we recall that some functions have a particularly nice property: to figure out its it at a value 2
3 x = a, one can simply substitute x = a into f(x). That is, we have f(x) = f(a). Such functions are known as continuous functions, and they are great because the it as x approaches a is just f(a). Example. Compute x 2 x 2 + 2x +. Solution: You previously learned that the function f(x) = x 2 + 2x + is continuous because it is a polynomial. Thus x 2 x2 + 2x + = () 2 + 2() + = 4. For multivariable functions, the definition is analogous: we say that a function f(x, y) is continuous if you can compute its it as (x, y) approaches (a, b) by simply substituting into f. We denote this by saying f(x, y) = f(a, b). (x,y) (a,b) Based on this, the question we should now be asking ourselves is: Which functions are continuous? In the single-variable world, the following functions are known to be continuous: Polynomials Exponentials Logarithms (if the number in the logarithm is positive) Sine and cosine Any combination of these (as long as there are no zero denominators, or negative numbers in a square root) It turns out that these types of functions are still continuous when you substitute more than one variable into them. Example 2. Compute the following it. xy + (x,y) (2,3) x2 y 2 3
4 Solution: Since the function f(x, y) = xy + is just a combination of polynomials, we need only substitute: xy + (x,y) (2,3) x2 y 2 = (2)(3) + (2) 2 (3) 2 = 42. Example 3. Compute the following it. cos(xy) + ex (x,y) (2,0) Solution: Since the function f(x, y) = cos(xy) + e x is just a combination of a cosine and an exponential, we need only substitute: cos(xy) + (x,y) (2,0) ex = cos((2)(0)) + e 2 = cos(0) + e = + e. 3 Discontinuous Functions The list of functions above seems to include every type of function we study in this course. This should lead you to ask the question: how can a function possibly be discontinuous? Consider the following example in one variable: suppose f(x) is the piecewise function { x if x 0 f(x) = if x < 0 You can check that but f(x) = 0 x 0 + f(x) =. x 0 Thus, the it at 0 does not exist. So we see that piecewise defined functions can be discontinuous. Example 4. Show that the function is not continuous at x = 0. f(x) = x 4
5 Solution: Since x 0 + x = + and x 0 x =, the function is not continuous. For multivariable functions, the situation can be a little more complicated. Recall from the picture above that when we say that (x, y) approaches (a, b), we are not specifying how we get there. In any way you approach (a, b), you have to get the same value of f(x, y). However, as we saw above, having either a piecewise defined function or a function with a denominator could cause problems, as we see in the following example. Example 5. Show that the it does not exist. (x,y) (0,0) x 4 + y 4 Solution: Suppose we choose a path for our coordinates (x, y) by specifying that we only choose coordinates of the type (x, 0). Then the fraction above will take the form x 2 (0) 2 x 4 + (0) 4 = 0. Thus (x,0) (0,0) x 4 + y 4 = 0. On the other hand, if we choose coordinates (x, y) where x = y, then the function takes the form Thus x 2 (x) 2 x 4 + (x) 4 = x4 2x 4 = 2. (x,x) (0,0) x 4 + y 4 = 2. So we have chosen two different paths by which we approach the origin (0, 0), and by doing so we arrive at two different answers. Thus the function cannot be continuous. 5
Exam 2 Review Sheet. r(t) = x(t), y(t), z(t)
 Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
You could identify a point on the graph of a function as (x,y) or (x, f(x)). You may have only one function value for each x number.
 Function Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second
Function Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second
Maxima and Minima. Terminology note: Do not confuse the maximum f(a, b) (a number) with the point (a, b) where the maximum occurs.
 10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
Math 232. Calculus III Limits and Continuity. Updated: January 13, 2016 Calculus III Section 14.2
 Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Section 15.3 Partial Derivatives
 Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Lecture 17 z-transforms 2
 Lecture 17 z-transforms 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/5/3 1 Factoring z-polynomials We can also factor z-transform polynomials to break down a large system into
Lecture 17 z-transforms 2 Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/5/3 1 Factoring z-polynomials We can also factor z-transform polynomials to break down a large system into
5.4 Transformations and Composition of Functions
 5.4 Transformations and Composition of Functions 1. Vertical Shifts: Suppose we are given y = f(x) and c > 0. (a) To graph y = f(x)+c, shift the graph of y = f(x) up by c. (b) To graph y = f(x) c, shift
5.4 Transformations and Composition of Functions 1. Vertical Shifts: Suppose we are given y = f(x) and c > 0. (a) To graph y = f(x)+c, shift the graph of y = f(x) up by c. (b) To graph y = f(x) c, shift
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Modular Arithmetic. Kieran Cooney - February 18, 2016
 Modular Arithmetic Kieran Cooney - kieran.cooney@hotmail.com February 18, 2016 Sums and products in modular arithmetic Almost all of elementary number theory follows from one very basic theorem: Theorem.
Modular Arithmetic Kieran Cooney - kieran.cooney@hotmail.com February 18, 2016 Sums and products in modular arithmetic Almost all of elementary number theory follows from one very basic theorem: Theorem.
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
14.2 Limits and Continuity
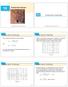 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
HW#02 (18 pts): All recommended exercises from JIT (1 pt/problem)
 Spring 2011 MthSc103 Course Calendar Page 1 of 7 January W 12 Syllabus/Course Policies BST Review Th 13 Basic Skills Test F 14 JIT 1.1 1.3: Numbers, Fractions, Parentheses JIT 1.1: 2, 6, 8, 9 JIT 1.2:
Spring 2011 MthSc103 Course Calendar Page 1 of 7 January W 12 Syllabus/Course Policies BST Review Th 13 Basic Skills Test F 14 JIT 1.1 1.3: Numbers, Fractions, Parentheses JIT 1.1: 2, 6, 8, 9 JIT 1.2:
MATH 12 CLASS 9 NOTES, OCT Contents 1. Tangent planes 1 2. Definition of differentiability 3 3. Differentials 4
 MATH 2 CLASS 9 NOTES, OCT 0 20 Contents. Tangent planes 2. Definition of differentiability 3 3. Differentials 4. Tangent planes Recall that the derivative of a single variable function can be interpreted
MATH 2 CLASS 9 NOTES, OCT 0 20 Contents. Tangent planes 2. Definition of differentiability 3 3. Differentials 4. Tangent planes Recall that the derivative of a single variable function can be interpreted
11.2 LIMITS AND CONTINUITY
 11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
The Chain Rule, Higher Partial Derivatives & Opti- mization
 The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
UNIT 2: FACTOR QUADRATIC EXPRESSIONS. By the end of this unit, I will be able to:
 UNIT 2: FACTOR QUADRATIC EXPRESSIONS UNIT 2 By the end of this unit, I will be able to: o Represent situations using quadratic expressions in one variable o Expand and simplify quadratic expressions in
UNIT 2: FACTOR QUADRATIC EXPRESSIONS UNIT 2 By the end of this unit, I will be able to: o Represent situations using quadratic expressions in one variable o Expand and simplify quadratic expressions in
Section 7.2 Logarithmic Functions
 Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Math 233. Extrema of Functions of Two Variables Basics
 Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
INTEGRATION OVER NON-RECTANGULAR REGIONS. Contents 1. A slightly more general form of Fubini s Theorem
 INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
18.3. Stationary Points. Introduction. Prerequisites. Learning Outcomes
 Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Partial Differentiation 1 Introduction
 Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
MA10103: Foundation Mathematics I. Lecture Notes Week 3
 MA10103: Foundation Mathematics I Lecture Notes Week 3 Indices/Powers In an expression a n, a is called the base and n is called the index or power or exponent. Multiplication/Division of Powers a 3 a
MA10103: Foundation Mathematics I Lecture Notes Week 3 Indices/Powers In an expression a n, a is called the base and n is called the index or power or exponent. Multiplication/Division of Powers a 3 a
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Logarithms. Since perhaps it s been a while, calculate a few logarithms just to warm up.
 Logarithms Since perhaps it s been a while, calculate a few logarithms just to warm up. 1. Calculate the following. (a) log 3 (27) = (b) log 9 (27) = (c) log 3 ( 1 9 ) = (d) ln(e 3 ) = (e) log( 100) =
Logarithms Since perhaps it s been a while, calculate a few logarithms just to warm up. 1. Calculate the following. (a) log 3 (27) = (b) log 9 (27) = (c) log 3 ( 1 9 ) = (d) ln(e 3 ) = (e) log( 100) =
LESSON 18: INTRODUCTION TO FUNCTIONS OF SEVERAL VARIABLES MATH FALL 2018
 LESSON 8: INTRODUCTION TO FUNCTIONS OF SEVERAL VARIABLES MATH 6020 FALL 208 ELLEN WELD. Partial Derivatives We aress how to take a erivative of a function of several variables. Although we won t get into
LESSON 8: INTRODUCTION TO FUNCTIONS OF SEVERAL VARIABLES MATH 6020 FALL 208 ELLEN WELD. Partial Derivatives We aress how to take a erivative of a function of several variables. Although we won t get into
14.7 Maximum and Minimum Values
 CHAPTER 14. PARTIAL DERIVATIVES 115 14.7 Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at
CHAPTER 14. PARTIAL DERIVATIVES 115 14.7 Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at
You found trigonometric values using the unit circle. (Lesson 4-3)
 You found trigonometric values using the unit circle. (Lesson 4-3) LEQ: How do we identify and use basic trigonometric identities to find trigonometric values & use basic trigonometric identities to simplify
You found trigonometric values using the unit circle. (Lesson 4-3) LEQ: How do we identify and use basic trigonometric identities to find trigonometric values & use basic trigonometric identities to simplify
Chapter 3 Exponential and Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions Section 1 Section 2 Section 3 Section 4 Section 5 Exponential Functions and Their Graphs Logarithmic Functions and Their Graphs Properties of Logarithms
Chapter 3 Exponential and Logarithmic Functions Section 1 Section 2 Section 3 Section 4 Section 5 Exponential Functions and Their Graphs Logarithmic Functions and Their Graphs Properties of Logarithms
LECTURE 19 - LAGRANGE MULTIPLIERS
 LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
Math Lecture 2 Inverse Functions & Logarithms
 Math 1060 Lecture 2 Inverse Functions & Logarithms Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms
Math 1060 Lecture 2 Inverse Functions & Logarithms Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms
Lecture 15. Global extrema and Lagrange multipliers. Dan Nichols MATH 233, Spring 2018 University of Massachusetts
 Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Contents. 1 Matlab basics How to start/exit Matlab Changing directory Matlab help... 2
 Contents 1 Matlab basics 2 1.1 How to start/exit Matlab............................ 2 1.2 Changing directory............................... 2 1.3 Matlab help................................... 2 2 Symbolic
Contents 1 Matlab basics 2 1.1 How to start/exit Matlab............................ 2 1.2 Changing directory............................... 2 1.3 Matlab help................................... 2 2 Symbolic
Piecewise Linear Circuits
 Kenneth A. Kuhn March 24, 2004 Introduction Piecewise linear circuits are used to approximate non-linear functions such as sine, square-root, logarithmic, exponential, etc. The quality of the approximation
Kenneth A. Kuhn March 24, 2004 Introduction Piecewise linear circuits are used to approximate non-linear functions such as sine, square-root, logarithmic, exponential, etc. The quality of the approximation
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables
 Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Math 32, October 22 & 27: Maxima & Minima
 Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
We could also take square roots of certain decimals nicely. For example, 0.36=0.6 or 0.09=0.3. However, we will limit ourselves to integers for now.
 7.3 Evaluation of Roots Previously we used the square root to help us approximate irrational numbers. Now we will expand beyond just square roots and talk about cube roots as well. For both we will be
7.3 Evaluation of Roots Previously we used the square root to help us approximate irrational numbers. Now we will expand beyond just square roots and talk about cube roots as well. For both we will be
An interesting class of problems of a computational nature ask for the standard residue of a power of a number, e.g.,
 Binary exponentiation An interesting class of problems of a computational nature ask for the standard residue of a power of a number, e.g., What are the last two digits of the number 2 284? In the absence
Binary exponentiation An interesting class of problems of a computational nature ask for the standard residue of a power of a number, e.g., What are the last two digits of the number 2 284? In the absence
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
NOTES: SIGNED INTEGERS DAY 1
 NOTES: SIGNED INTEGERS DAY 1 MULTIPLYING and DIVIDING: Same Signs (POSITIVE) + + = + positive x positive = positive = + negative x negative = positive Different Signs (NEGATIVE) + = positive x negative
NOTES: SIGNED INTEGERS DAY 1 MULTIPLYING and DIVIDING: Same Signs (POSITIVE) + + = + positive x positive = positive = + negative x negative = positive Different Signs (NEGATIVE) + = positive x negative
PREREQUISITE/PRE-CALCULUS REVIEW
 PREREQUISITE/PRE-CALCULUS REVIEW Introduction This review sheet is a summary of most of the main topics that you should already be familiar with from your pre-calculus and trigonometry course(s), and which
PREREQUISITE/PRE-CALCULUS REVIEW Introduction This review sheet is a summary of most of the main topics that you should already be familiar with from your pre-calculus and trigonometry course(s), and which
Math 122: Final Exam Review Sheet
 Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
Algebra/Geometry Session Problems Questions 1-20 multiple choice
 lgebra/geometry Session Problems Questions 1-0 multiple choice nswer only one choice: (a), (b), (c), (d), or (e) for each of the following questions. Only use a number pencil. Make heavy black marks that
lgebra/geometry Session Problems Questions 1-0 multiple choice nswer only one choice: (a), (b), (c), (d), or (e) for each of the following questions. Only use a number pencil. Make heavy black marks that
Chapter 11 Trigonometric Ratios The Sine Ratio
 Chapter 11 Trigonometric Ratios 11.2 The Sine Ratio Introduction The figure below shows a right-angled triangle ABC, where B = and C = 90. A hypotenuse B θ adjacent side of opposite side of C AB is called
Chapter 11 Trigonometric Ratios 11.2 The Sine Ratio Introduction The figure below shows a right-angled triangle ABC, where B = and C = 90. A hypotenuse B θ adjacent side of opposite side of C AB is called
LECTURE 7: POLYNOMIAL CONGRUENCES TO PRIME POWER MODULI
 LECTURE 7: POLYNOMIAL CONGRUENCES TO PRIME POWER MODULI 1. Hensel Lemma for nonsingular solutions Although there is no analogue of Lagrange s Theorem for prime power moduli, there is an algorithm for determining
LECTURE 7: POLYNOMIAL CONGRUENCES TO PRIME POWER MODULI 1. Hensel Lemma for nonsingular solutions Although there is no analogue of Lagrange s Theorem for prime power moduli, there is an algorithm for determining
cos sin sin 2 60 = 1.
 Name: Class: Date: Use the definitions to evaluate the six trigonometric functions of. In cases in which a radical occurs in a denominator, rationalize the denominator. Suppose that ABC is a right triangle
Name: Class: Date: Use the definitions to evaluate the six trigonometric functions of. In cases in which a radical occurs in a denominator, rationalize the denominator. Suppose that ABC is a right triangle
Lesson 16: The Computation of the Slope of a Non Vertical Line
 ++ Lesson 16: The Computation of the Slope of a Non Vertical Line Student Outcomes Students use similar triangles to explain why the slope is the same between any two distinct points on a non vertical
++ Lesson 16: The Computation of the Slope of a Non Vertical Line Student Outcomes Students use similar triangles to explain why the slope is the same between any two distinct points on a non vertical
College Pre-Calc Lesson Plans
 January 4-8 January 11-15 January 18-22 January 25-29 Sections 9.2 Area of a Triangle Mixed Trig Exercises Section 14.1 Matrix Addition & Scalar Multiplication Section 14.5 Transition Pg 342: 1, 3, 7-13,
January 4-8 January 11-15 January 18-22 January 25-29 Sections 9.2 Area of a Triangle Mixed Trig Exercises Section 14.1 Matrix Addition & Scalar Multiplication Section 14.5 Transition Pg 342: 1, 3, 7-13,
1 Graphs of Sine and Cosine
 1 Graphs of Sine and Cosine Exercise 1 Sketch a graph of y = cos(t). Label the multiples of π 2 and π 4 on your plot, as well as the amplitude and the period of the function. (Feel free to sketch the unit
1 Graphs of Sine and Cosine Exercise 1 Sketch a graph of y = cos(t). Label the multiples of π 2 and π 4 on your plot, as well as the amplitude and the period of the function. (Feel free to sketch the unit
Primitive Roots. Chapter Orders and Primitive Roots
 Chapter 5 Primitive Roots The name primitive root applies to a number a whose powers can be used to represent a reduced residue system modulo n. Primitive roots are therefore generators in that sense,
Chapter 5 Primitive Roots The name primitive root applies to a number a whose powers can be used to represent a reduced residue system modulo n. Primitive roots are therefore generators in that sense,
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers
 SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A
 Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
CHAPTER 11 PARTIAL DERIVATIVES
 CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
By Scott Fallstrom and Brent Pickett The How and Whys Guys
 Math Fundamentals for Statistics I (Math 52) Unit 2:Number Line and Ordering By Scott Fallstrom and Brent Pickett The How and Whys Guys This work is licensed under a Creative Commons Attribution- NonCommercial-ShareAlike
Math Fundamentals for Statistics I (Math 52) Unit 2:Number Line and Ordering By Scott Fallstrom and Brent Pickett The How and Whys Guys This work is licensed under a Creative Commons Attribution- NonCommercial-ShareAlike
Lecture 4 : Monday April 6th
 Lecture 4 : Monday April 6th jacques@ucsd.edu Key concepts : Tangent hyperplane, Gradient, Directional derivative, Level curve Know how to find equation of tangent hyperplane, gradient, directional derivatives,
Lecture 4 : Monday April 6th jacques@ucsd.edu Key concepts : Tangent hyperplane, Gradient, Directional derivative, Level curve Know how to find equation of tangent hyperplane, gradient, directional derivatives,
Independence of Path and Conservative Vector Fields
 Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
r = (a cos θ, b sin θ). (1.1)
 Peeter Joot peeter.joot@gmail.com Circumference of an ellipse 1.1 Motivation Lance told me they ve been covering the circumference of a circle in school this week. This made me think of the generalization
Peeter Joot peeter.joot@gmail.com Circumference of an ellipse 1.1 Motivation Lance told me they ve been covering the circumference of a circle in school this week. This made me think of the generalization
Math Fundamentals for Statistics (Math 52) Unit 2:Number Line and Ordering. By Scott Fallstrom and Brent Pickett The How and Whys Guys.
 Math Fundamentals for Statistics (Math 52) Unit 2:Number Line and Ordering By Scott Fallstrom and Brent Pickett The How and Whys Guys Unit 2 Page 1 2.1: Place Values We just looked at graphing ordered
Math Fundamentals for Statistics (Math 52) Unit 2:Number Line and Ordering By Scott Fallstrom and Brent Pickett The How and Whys Guys Unit 2 Page 1 2.1: Place Values We just looked at graphing ordered
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
(1) 2 x 6. (2) 5 x 8. (3) 9 x 12. (4) 11 x 14. (5) 13 x 18. Soln: Initial quantity of rice is x. After 1st customer, rice available In the Same way
 1. A shop stores x kg of rice. The first customer buys half this amount plus half a kg of rice. The second customer buys half the remaining amount plus half a kg of rice. Then the third customer also buys
1. A shop stores x kg of rice. The first customer buys half this amount plus half a kg of rice. The second customer buys half the remaining amount plus half a kg of rice. Then the third customer also buys
MATH 8 FALL 2010 CLASS 27, 11/19/ Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits
 MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
Comparing Exponential and Logarithmic Rules
 Name _ Date Period Comparing Exponential and Logarithmic Rules Task : Looking closely at exponential and logarithmic patterns ) In a prior lesson you graphed and then compared an exponential function with
Name _ Date Period Comparing Exponential and Logarithmic Rules Task : Looking closely at exponential and logarithmic patterns ) In a prior lesson you graphed and then compared an exponential function with
Review Problems. Calculus IIIA: page 1 of??
 Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
Honors Algebra 2 Assignment Sheet - Chapter 1
 Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and
![[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and [f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and](/thumbs/92/108353356.jpg) Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Chapter 9 Linear equations/graphing. 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane
 Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
Sect 4.5 Inequalities Involving Quadratic Function
 71 Sect 4. Inequalities Involving Quadratic Function Objective #0: Solving Inequalities using a graph Use the graph to the right to find the following: Ex. 1 a) Find the intervals where f(x) > 0. b) Find
71 Sect 4. Inequalities Involving Quadratic Function Objective #0: Solving Inequalities using a graph Use the graph to the right to find the following: Ex. 1 a) Find the intervals where f(x) > 0. b) Find
Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi
 Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture - 23 The Phase Locked Loop (Contd.) We will now continue our discussion
Communication Engineering Prof. Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Lecture - 23 The Phase Locked Loop (Contd.) We will now continue our discussion
Discussion 8 Solution Thursday, February 10th. Consider the function f(x, y) := y 2 x 2.
 Discussion 8 Solution Thursday, February 10th. 1. Consider the function f(x, y) := y 2 x 2. (a) This function is a mapping from R n to R m. Determine the values of n and m. The value of n is 2 corresponding
Discussion 8 Solution Thursday, February 10th. 1. Consider the function f(x, y) := y 2 x 2. (a) This function is a mapping from R n to R m. Determine the values of n and m. The value of n is 2 corresponding
Prolegomena. Chapter Using Interval Notation 1
 Chapter 1 Prolegomena 1.1 Using Interval Notation 1 Interval notation is another method for writing domain and range. In set builder notation braces (curly parentheses {} ) and variables are used to express
Chapter 1 Prolegomena 1.1 Using Interval Notation 1 Interval notation is another method for writing domain and range. In set builder notation braces (curly parentheses {} ) and variables are used to express
WARM UP. 1. Expand the expression (x 2 + 3) Factor the expression x 2 2x Find the roots of 4x 2 x + 1 by graphing.
 WARM UP Monday, December 8, 2014 1. Expand the expression (x 2 + 3) 2 2. Factor the expression x 2 2x 8 3. Find the roots of 4x 2 x + 1 by graphing. 1 2 3 4 5 6 7 8 9 10 Objectives Distinguish between
WARM UP Monday, December 8, 2014 1. Expand the expression (x 2 + 3) 2 2. Factor the expression x 2 2x 8 3. Find the roots of 4x 2 x + 1 by graphing. 1 2 3 4 5 6 7 8 9 10 Objectives Distinguish between
18.S34 (FALL, 2007) PROBLEMS ON PROBABILITY
 18.S34 (FALL, 2007) PROBLEMS ON PROBABILITY 1. Three closed boxes lie on a table. One box (you don t know which) contains a $1000 bill. The others are empty. After paying an entry fee, you play the following
18.S34 (FALL, 2007) PROBLEMS ON PROBABILITY 1. Three closed boxes lie on a table. One box (you don t know which) contains a $1000 bill. The others are empty. After paying an entry fee, you play the following
Analog Circuits Prof. Jayanta Mukherjee Department of Electrical Engineering Indian Institute of Technology-Bombay
 Analog Circuits Prof. Jayanta Mukherjee Department of Electrical Engineering Indian Institute of Technology-Bombay Week -02 Module -01 Non Idealities in Op-Amp (Finite Gain, Finite Bandwidth and Slew Rate)
Analog Circuits Prof. Jayanta Mukherjee Department of Electrical Engineering Indian Institute of Technology-Bombay Week -02 Module -01 Non Idealities in Op-Amp (Finite Gain, Finite Bandwidth and Slew Rate)
Honors Algebra 2 w/ Trigonometry Chapter 14: Trigonometric Identities & Equations Target Goals
 Honors Algebra w/ Trigonometry Chapter 14: Trigonometric Identities & Equations Target Goals By the end of this chapter, you should be able to Identify trigonometric identities. (14.1) Factor trigonometric
Honors Algebra w/ Trigonometry Chapter 14: Trigonometric Identities & Equations Target Goals By the end of this chapter, you should be able to Identify trigonometric identities. (14.1) Factor trigonometric
An ordered collection of counters in rows or columns, showing multiplication facts.
 Addend A number which is added to another number. Addition When a set of numbers are added together. E.g. 5 + 3 or 6 + 2 + 4 The answer is called the sum or the total and is shown by the equals sign (=)
Addend A number which is added to another number. Addition When a set of numbers are added together. E.g. 5 + 3 or 6 + 2 + 4 The answer is called the sum or the total and is shown by the equals sign (=)
3.2 Proving Identities
 3.. Proving Identities www.ck.org 3. Proving Identities Learning Objectives Prove identities using several techniques. Working with Trigonometric Identities During the course, you will see complex trigonometric
3.. Proving Identities www.ck.org 3. Proving Identities Learning Objectives Prove identities using several techniques. Working with Trigonometric Identities During the course, you will see complex trigonometric
Sect Linear Equations in Two Variables
 99 Concept # Sect. - Linear Equations in Two Variables Solutions to Linear Equations in Two Variables In this chapter, we will examine linear equations involving two variables. Such equations have an infinite
99 Concept # Sect. - Linear Equations in Two Variables Solutions to Linear Equations in Two Variables In this chapter, we will examine linear equations involving two variables. Such equations have an infinite
Math 5BI: Problem Set 1 Linearizing functions of several variables
 Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
J.7 Properties of Logarithms
 J.7. PROPERTIES OF LOGARITHMS 1 J.7 Properties of Logarithms J.7.1 Understanding Properties of Logarithms Product Rule of Logarithms log a MN = log a M +log a N Example J.7.1. Rewrite as a sum of logarithms:
J.7. PROPERTIES OF LOGARITHMS 1 J.7 Properties of Logarithms J.7.1 Understanding Properties of Logarithms Product Rule of Logarithms log a MN = log a M +log a N Example J.7.1. Rewrite as a sum of logarithms:
Graphing Sine and Cosine
 The problem with average monthly temperatures on the preview worksheet is an example of a periodic function. Periodic functions are defined on p.254 Periodic functions repeat themselves each period. The
The problem with average monthly temperatures on the preview worksheet is an example of a periodic function. Periodic functions are defined on p.254 Periodic functions repeat themselves each period. The
Double-Angle, Half-Angle, and Reduction Formulas
 Double-Angle, Half-Angle, and Reduction Formulas By: OpenStaxCollege Bicycle ramps for advanced riders have a steeper incline than those designed for novices. Bicycle ramps made for competition (see [link])
Double-Angle, Half-Angle, and Reduction Formulas By: OpenStaxCollege Bicycle ramps for advanced riders have a steeper incline than those designed for novices. Bicycle ramps made for competition (see [link])
Math 259 Winter Recitation Handout 6: Limits in Two Dimensions
 Math 259 Winter 2009 Recitation Handout 6: its in Two Dimensions As we have discussed in lecture, investigating the behavior of functions with two variables, f(x, y), can be more difficult than functions
Math 259 Winter 2009 Recitation Handout 6: its in Two Dimensions As we have discussed in lecture, investigating the behavior of functions with two variables, f(x, y), can be more difficult than functions
Distribution of Primes
 Distribution of Primes Definition. For positive real numbers x, let π(x) be the number of prime numbers less than or equal to x. For example, π(1) = 0, π(10) = 4 and π(100) = 25. To use some ciphers, we
Distribution of Primes Definition. For positive real numbers x, let π(x) be the number of prime numbers less than or equal to x. For example, π(1) = 0, π(10) = 4 and π(100) = 25. To use some ciphers, we
REVIEW SHEET FOR MIDTERM 2: ADVANCED
 REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
Section 5.2 Graphs of the Sine and Cosine Functions
 A Periodic Function and Its Period Section 5.2 Graphs of the Sine and Cosine Functions A nonconstant function f is said to be periodic if there is a number p > 0 such that f(x + p) = f(x) for all x in
A Periodic Function and Its Period Section 5.2 Graphs of the Sine and Cosine Functions A nonconstant function f is said to be periodic if there is a number p > 0 such that f(x + p) = f(x) for all x in
Unit 8 Trigonometry. Math III Mrs. Valentine
 Unit 8 Trigonometry Math III Mrs. Valentine 8A.1 Angles and Periodic Data * Identifying Cycles and Periods * A periodic function is a function that repeats a pattern of y- values (outputs) at regular intervals.
Unit 8 Trigonometry Math III Mrs. Valentine 8A.1 Angles and Periodic Data * Identifying Cycles and Periods * A periodic function is a function that repeats a pattern of y- values (outputs) at regular intervals.
Higher. Expressions & Functions. Unit 2 Course Contents. Higher Higher Higher Higher Higher. Higher Higher. Higher Higher. Higher Higher.
 Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher xpressions & unctions Unit 2 Course Contents Higher
Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher xpressions & unctions Unit 2 Course Contents Higher
4.3. Trigonometric Identities. Introduction. Prerequisites. Learning Outcomes
 Trigonometric Identities 4.3 Introduction trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles. There are a very large number
Trigonometric Identities 4.3 Introduction trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles. There are a very large number
23 Applications of Probability to Combinatorics
 November 17, 2017 23 Applications of Probability to Combinatorics William T. Trotter trotter@math.gatech.edu Foreword Disclaimer Many of our examples will deal with games of chance and the notion of gambling.
November 17, 2017 23 Applications of Probability to Combinatorics William T. Trotter trotter@math.gatech.edu Foreword Disclaimer Many of our examples will deal with games of chance and the notion of gambling.
Solutions to the problems from Written assignment 2 Math 222 Winter 2015
 Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
MULTI-VARIABLE OPTIMIZATION NOTES. 1. Identifying Critical Points
 MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MATH 234 THIRD SEMESTER CALCULUS
 MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
To process an image so that the result is more suitable than the original image for a specific application.
 by Shahid Farid 1 To process an image so that the result is more suitable than the original image for a specific application. Categories: Spatial domain methods and Frequency domain methods 2 Procedures
by Shahid Farid 1 To process an image so that the result is more suitable than the original image for a specific application. Categories: Spatial domain methods and Frequency domain methods 2 Procedures
P1 Chapter 10 :: Trigonometric Identities & Equations
 P1 Chapter 10 :: Trigonometric Identities & Equations jfrost@tiffin.kingston.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 20 th August 2017 Use of DrFrostMaths for practice Register for free
P1 Chapter 10 :: Trigonometric Identities & Equations jfrost@tiffin.kingston.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 20 th August 2017 Use of DrFrostMaths for practice Register for free
UNC Charlotte 2002 Comprehensive. March 4, 2002
 UNC Charlotte March 4, 2002 1 It takes 852 digits to number the pages of a book consecutively How many pages are there in the book? A) 184 B) 235 C) 320 D) 368 E) 425 2 Solve the equation 8 1 6 + x 1 3
UNC Charlotte March 4, 2002 1 It takes 852 digits to number the pages of a book consecutively How many pages are there in the book? A) 184 B) 235 C) 320 D) 368 E) 425 2 Solve the equation 8 1 6 + x 1 3
The Discrete Fourier Transform. Claudia Feregrino-Uribe, Alicia Morales-Reyes Original material: Dr. René Cumplido
 The Discrete Fourier Transform Claudia Feregrino-Uribe, Alicia Morales-Reyes Original material: Dr. René Cumplido CCC-INAOE Autumn 2015 The Discrete Fourier Transform Fourier analysis is a family of mathematical
The Discrete Fourier Transform Claudia Feregrino-Uribe, Alicia Morales-Reyes Original material: Dr. René Cumplido CCC-INAOE Autumn 2015 The Discrete Fourier Transform Fourier analysis is a family of mathematical
Modular arithmetic Math 2320
 Modular arithmetic Math 220 Fix an integer m 2, called the modulus. For any other integer a, we can use the division algorithm to write a = qm + r. The reduction of a modulo m is the remainder r resulting
Modular arithmetic Math 220 Fix an integer m 2, called the modulus. For any other integer a, we can use the division algorithm to write a = qm + r. The reduction of a modulo m is the remainder r resulting
Topic 6: Joint Distributions
 Topic 6: Joint Distributions Course 003, 2017 Page 0 Joint distributions Social scientists are typically interested in the relationship between many random variables. They may be able to change some of
Topic 6: Joint Distributions Course 003, 2017 Page 0 Joint distributions Social scientists are typically interested in the relationship between many random variables. They may be able to change some of
S56 (5.1) Logs and Exponentials.notebook October 14, 2016
 1. Daily Practice 21.9.2016 Exponential Functions Today we will be learning about exponential functions. A function of the form y = a x is called an exponential function with the base 'a' where a 0. y
1. Daily Practice 21.9.2016 Exponential Functions Today we will be learning about exponential functions. A function of the form y = a x is called an exponential function with the base 'a' where a 0. y
