14.7 Maximum and Minimum Values
|
|
|
- Shavonne Pierce
- 5 years ago
- Views:
Transcription
1 CHAPTER 14. PARTIAL DERIVATIVES Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at (a, b) iff(a, b) apple f(x, y) for all (x, y) near (a, b). f has an absolute max at (a, b) iff(a, b) f(x, y) for all (x, y) in the domain. f has an absolute min at (a, b) iff(a, b) apple f(x, y) for all (x, y) in the domain. The number f(a, b) is called the maximum value or minimum value. Theorem. Let f have a local maximum or minimum at (a, b). Then each partial derivative, f x (a, b) and f y (a, b), either equals 0 or does not exist. In particular, if the partial derivatives exist, then max means f(a, b) f(x, y), min means f(a, b) apple f(x, y). Local means (x, y) nearby, absolute means all (x, y) in domain. Local max/min implies rf = 0 (or DNE). rf(a, b) =0. Proof. We can reduce this statement to Calculus I by taking the traces. For instance, the y = b trace gives a function of just one variable, f(x, b). This function has a local max or min at x = a, and so f x (x, b) equals 0 or does not exist at x = a. Definition. We say ha, bi is a critical point of f(x, y) ifrf(a, b) =0 or at least one of the partial derivatives is undefined. Example 1. Find the critical points of f(x, y) =x 2 + y 2 them as local max/min/neither. 4x +8y + 10 and identify f x =2x 4=0 2x 4=0 x =2 f y =2y +8 2y +8=0 y = 4 ha, bi = h2, We will learn a version of the 2nd derivative test below to figure out if this point is a max/min/neither. But in this case we can figure it out with some algebra. Specifically, we ll complete the square: f(x, y) =(x 2 4x + 4) + (y 2 +8y + 16) f(x, y) = 4i =(x 2) 2 +(y + 4) positive numbers 10 for all x, y f(2, 4) = 10 is abs/local min
2 CHAPTER 14. PARTIAL DERIVATIVES 116 Definition (2nd Derivative Test). Suppose (a, b) is a critical point of f with f x (a, b) =f y (a, b) = 0 and suppose all the 2nd partial derivatives are continuous at and near (a, b). Let D = D(a, b) =f xx (a, b) f yy (a, b) 2 f xy (a, b) Let D = f xx f yy (f xy ) 2. (1) D>0, f xx < 0, min, (2) D>0, f xx > 0, max, (3) D<0, neither, (4) D = 0, try something else. 1. If D>0 and f xx (a, b) > 0thenf(a, b) is a local min. 2. If D>0 and f xx (a, b) < 0thenf(a, b) is a local max. 3. If D < 0thenf(a, b) is neither a max nor min and (a, b) isa saddle point. 4. If D = 0, then the 2nd derivative test is gives you no information. 2 Comments. 1. We can write D in other ways. Note that f xy (a, b) = fxy (a, b) f yx (ab) = 2 f yx (a, b) so we can use either fxy or f yx or both to calculate D. 2. In conditions (1) and (2), instead of f xx (a, b) > 0 or f xx (a, b) < 0, we can use f yy (a, b) > 0 or f yy (a, b) < 0 without changing any other details of the test. In e ect, the condition D >0 means that the information we get from f xx and from f yy will be the same (i.e. if D>0thenf xx < 0 () f yy < 0 and f xx > 0 () f yy > 0). 3. We can remember D using matrices: it is the determinant of the matrix of second partial derivatives: D = f xx(a, b) f xy (a, b) f yx (a, b) f yy (a, b) Furthermore, the matrix of all second partial derivatives is called the Hessian matrix. Below in a few examples we will occasionally use the notation r 2 f(x, y) for the matrix of second order partial derivatives. Example 2. Apply the second derivative test to to identify the local/max/min/neither of f(x, y) =x 2 + y 2 4x +8y f x =2x 4 f y =2y +8 (2, 4) = critical pt f xx =2 f yy =2 f yx = f xy =0 This is where we ended on Thursday, February 28 D = =4 D>0 and f xx (2, 4) = 2 > 0so(2, 4) is a local min. Example 3. Find the critical points and identify them as local max/min/neither for
3 CHAPTER 14. PARTIAL DERIVATIVES 117 the function f(x, y) =x 4 y 4. f x =4x 3 f y = 4y 3 (0, 0) = critical pt apple r 2 12x 2 0 f = 0 12y 2 D(0, 0) = =0. Since D = 0, the Second Derivative Test doesn t help. To finish, we look at traces y = 0 trace: f(x, 0) = x 4 x = 0 trace: f(0,y)= y 4 x = 0 is local min y = 0 is local max (0, 0) is saddle point Absolute Maximum and Minimum Comments. Recall the Extreme Value Theorem of Calculus I, also known as the Absolute Max/Min Test. It said two things. (1) Every continuous function defined on an interval [a, b] always has an absolute maximum and an absolute minimum. (2) To find the absolute max/min you (i) find the critical points, (ii) evaluate the function at each critical point and each endpoint, (iii) identify the largest/smallest values calculated in step (ii) as the absolute max/mins. Theorem (Extreme Value Theorem). Let f be a continuous function defined on a closed and bounded domain D R 2. Then f has an absolute maximum an absolute minimum on D. Tofindthemdothe following: 1. Find the critical points of f in D, 2. Evaluate f at each critical point, 3. Find the absolute maximum and minimum values of f on the boundary of D (usually using Calculus I methods, or Lagrange Multipliers in the next section), 4. Identify the largest/smallest values calculated in steps (2) and (3) as the absolute max/mins. Given f contin, D closed bounded. (1) Find crit. pts in D, (2) Evaluate f, (3) Find max/mins on boundary of D, (4) Compare values. Example 4. Let f(x, y) =xy 2, D = {x 0, y 0, x 2 + y 2 apple 3}. Find the absolute maximum and minimum values of f on D. Let s start by identifying D a little better. It is part of a circle with radius p 3, in Quadrant I:
4 CHAPTER 14. PARTIAL DERIVATIVES 118 This domain is bounded, because it does not extend infinitely far in any direction, and it is closed, because it includes its boundary (since the definition had x 0 not just x>0, and similarly y 0 not just y>0 and x 2 + y 2 apple 3 and not just x 2 + y 2 < 3). Now we find the critical points: f x = y 2 y 2 =0 y =0 f y =2xy 2xy =0 x = 0 or y =0 In other words the critical points are all along the x-axis. Since this is also the boundary of the domain D, we ll find the max/min values of f on these critical points in steps (2) and (3). We start by breaking the boundary of D down into three pieces: boundary of D = D 1 [ D 2 [ D 3 D 1 = x-axis from 0 to p 3 D 2 = y-axis from 0 to p 3 D 3 = Quadrant I part of circle x 2 + y 2 =3 Now we figure out the absolute max/min of f on each of these sets: f on D 1 : f(x, 0) = 0 f on D 2 : f(0,y)=0 f on D 3 : f(x, y) =? x 2 + y 2 =3 y = p 3 x 2 f(x, y) =f(x, p 3 x 2 ) = x(3 x 2 ) Now we use Calculus I with the function g(x) =x(3 x 2 ) on the domain [0, p 3]. g(x) =3x x 3, [0, p 3] g 0 (x) =3 3x 2 3 3x 2 =0 x = ±1
5 CHAPTER 14. PARTIAL DERIVATIVES 119 x =1, since x = g(0) = 0 g(1) = 3(1) 1 3 =2 g( p 3) = 3 p 3 ( p 3) 3 = p 3 3 ( p 3) 2 =0 1 is not in the domain So we see that g has absolute min at x = 0 or x = p 3, with value 0, and absolute max at x = 1 with value 2. Translating this back to f we get: y = p 3 x 2 x =0: f(x, y) = 0 everywhere on D 1 x =1: y = p y = p 2 x = p q 3: y = 3 ( p 3) 2 y =0 Abs Max f(1, p 2) = 2 f(x, y) = 0 everywhere on D 2 Abs Min f(x, y) = 0 everywhere on D 1 [ D 2 This is where we ended on Friday, March 1 Extra Example This extra example is very similar to some homework problems, and should be studied like the preceeding examples. Example 5. [Stewart 6e, #32] Find the absolute max and min of the following function on the indicated domain: We find the critical points where f(x, y) =4x +6y x 2 y 2 D = {(x, y) 0 apple x apple 4, 0 apple y apple 5} h 2x +4, 2y +6i = h0, 0i rf = h 2x +4, 2y +6i hx, yi = h2, 3i f(2, 3) = 13 Now we break the boundary of the domain into 4 pieces: Boundary of D = D 1 [ D 2 [ D 3 [ D 4 D 1 : y =0, x is in [0, 4]
6 CHAPTER 14. PARTIAL DERIVATIVES 120 D 2 : x =4, y is in [0, 5] D 3 : y =5, x is in [0, 4] D 4 : x =0, y is in [0, 5] Now we have a series of Calculus I problems: D 1 : find max/min of g 1 (x) =f(x, 0) = 4x x 2, on [0, 4] D 2 : find max/min of g 2 (y) =f(4,y) = y 16 y 2 =6y y 2 on [0, 5] D 3 : find max/min of g 3 (x) =f(x, 5) = 4x x on [0, 4] D 4 : find max/min of g 4 (x) =f(0,y)=6y y 2 on [0, 5] Calc I on D 1 : g 1 (x) =4x x 2, on [0, 4] g1(x) 0 = 2x +4 2x +4=0) x =2 g 1 (0) = 0 g 1 (2) = 4 g 1 (4) = 0 Calc I on D 2 : g 2 (y) =6y y 2 on [0, 5] g2(y) 0 = 2y +6 2y +6=0) y =3 g 2 (0) = 0 g 2 (3) = 18 9=9 g 2 (5) = = 5 Calc I on D 3 g 3 (x) =4x x on [0, 4] g3(x) 0 = 2x +4 2x +4=0) x =2 g 3 (0) = 5 g 3 (2) = 8 4+5=9 g 3 (4) = = 5 Calc I on D 4 : g 4 (x) =6y y 2 on [0, 5] g4(x) 0 = 2y +6 2y +6=0) y =3 g 4 (0) = 0 g 4 (3) = 18 9=9
7 CHAPTER 14. PARTIAL DERIVATIVES 121 g 4 (5) = = 5 After solving the above Calc I problems, and comparing values, you should get the following: f(x, y) : f(2, 3) = 13 g 1 (x) : g 1 (0) = 0, g 1 (2) = 4 g 1 (4) = 0 g 2 (y) : g 2 (0) = 0, g 2 (3) = 9, g 2 (5) = 5 g 3 (x) : g 3 (0) = 5, g 3 (2) = 9, g 3 (4) = 5 g 4 (y) : g 4 (0) = 0, g 4 (3) = 9, g 4 (5) = 5 From the above numbers, we simply want to identify the largest and smallest: Extra Optional Material abs max at (2, 3), value = 13 abs min at (4, 0) and (0, 0), value = 0 Everything in this subsection is kind of interesting, but does not need to be studied, and is not included on the homework or tests. Example 6. [The Ackley Function] The Ackley function was invented as a good test case for numerical algorithms that are designed to find maximums and minimums. We give a simplified version of it here (it can be generalized to higher dimensions, and various coe cients can be tweaked to change the relative size of the mins and maxs). f(x, y) = 10e 5p x 2 +y 2 e cos(2 x)+cos(2 y). Use a computer to find approximate values of the critical points, and the max and mins, on the domain 3 apple x apple 3 and 3 apple y apple 3, and identify them as local/global max/min. Comments. The second derivative test given above is the analogue in two variables of of the second derivative test from Calculus I. There is also a first derivative test analogue. Here s one way to state it. Theorem. Suppose f is continuous at (a, b) and di erentiable near (a, b). 1. If there exists an open disk around (a, b) such that for all (x, y) in that disk we have rf(x, y) hx a, y bi > 0then(a, b) is a local minimum. 2. If there exists an open disk around (a, b) such that for all (x, y) in that disk we have rf(x, y) hx a, y bi < 0then(a, b) is a local maximum. 3. If for all open disks around (a, b) we have some (x, y) inthediskwithrf(x, y) hx a, y bi < 0 and some (x, y) inthediskwithrf(x, y) hx a, y bi > 0, then (a, b) is neither a local max nor local min. (See by Michael W. Botsko in The American Mathematical Monthly, vol. 93, 1986, no. 7, pages ) Comments. 1. The conditions above are more easily understood as directional derivatives. The expression rf(x, y) hx a, y bi > 0 is equivalent to Duf(a + hu 1,b+ hu 2 ) > 0 where x = a + hu 1 and y = b + hu 2. Thus, if we ignore all the complicated parts of the statements about open disks, the previous theorem
8 CHAPTER 14. PARTIAL DERIVATIVES 122 basically says: if all the directional derivatives right around (a, b) are positive, then it s a local min, if all the directional derivatives right around (a, b) are negative, then it s a local max, and if some are positive and some are negative then it s neither. 2. In Calculus practice problems it s rare to find a problem where we need the full strength of part (3). In almost textbook problems instead of needing to look at all directional derivatives to find some that are positive and some that are negative. Really, we almost always get away with just needing to look at the directional derivatives just with respect to the directions h1, 0i and h0, 1i. This means we end up showing that the x-trace has a local max/min, and the y-trace has a local max/min, but one is a max and the other is a min. This is basically what happens in the example f(x, y) =x 4 y 4 above (which we repeat below using the First Derivative Test). Example 7. The article by Botsko mentioned above has this example: Use the first derivative test to show that the critical point (1, 2) of f(x, y) =x 2 +2xy +3y 2 +2x + 10y +9 We take the dot product approach from the previous theorem rf(x, y) hx 1, y+2i = h2x +2y +2, 2x +6y + 10i hx 1, y+2i =(2x +2y + 2)(x 1) + (2x +6y + 10)(y + 2). We can see now why the first derivative approach may not be easy to sort out: how can we hope to show that the above formula is > 0 or < 0? Well, remember it s only meant to be positive or negative for (x, y) su ciently close to (1, 2). Su ciently close means that both x 1 and y + 2 should be close to 0. Since x 1 and y + 2 are the crucial quantities, it would be easier to write the whole formula in terms of them. In other words, change variables. Using these variables we have let w = x 1 let v = y +2 then 2x +2y +2=2w +2v and 2x +6y + 10 = 2w +6v. (2x +2y + 2)(x 1) + (2x +6y + 10)(y + 2) = (2w +2v)w +(2w +6v)v = 2(w 2 + wv + wv +3v 2 ) =2 (w + v) 2 +2v 2 > 0 for all w and v Therefore, (1, 2) is a local minimum. The reader may see that we were a bit lucky here: the formula simplified rather well with the substitutions we made. But it s not so easy in general to factor a quadratic in two variables. Example 8. Apply the first derivative test to identify the behavior of f(x, y) =x 2 + y 2 4x +8y + 10 at the point (2, 4). rf(x, y) hx 2, y+4i = h2x 4, 2y +8i hx 2, y+4i
9 CHAPTER 14. PARTIAL DERIVATIVES 123 Therefore (2, 4) is a local minimum. =(2x 4)(x 2) + (2y + 8)(y + 4) = 2(x 2)(x 2) + 2(y + 4)(y + 4) = 2(x 2) 2 + 2(y + 4) 2 > 0 for all x and y. Example 9. Apply the first derivative test to the function and the critical point (0, 0). f(x, y) =x 4 y 4 rf(x, y) hx 0, y 0i = 4x 3, 4y 3 hx, yi =4x 4 4y 4 For any open disk around (0, 0) we can find an (x, y) value in the disk that makes this positive (for example x in the disk and y = 0) and we can find another (x, y) value that makes this negative (for example x = 0 and y in the disk). Therefore, this is a saddle point. Example 10. Apply the first derivative test to the function and the critical point (0, 0). Therefore (0, 0) is a local maximum. f(x, y) = x 4 y 4 rf(x, y) hx 0, y 0i = 4x 3, 4y 3 hx, yi = 4x 4 4y 4 < 0 for all x and y. Example 11. From the article by Botsko listed above we have more examples: (a) Apply the 1st derivative test to f(x, y) =1 x 2/3 y 4/5 at the critical point (0, 0). Show also that the second derivative test fails. (b) Apply the 1st derivative test to f(x, y) = 25 + (x y) 4 +(x 1) 4 at the critical point (1, 1). Show also that the second derivative test fails. (a) rf(x, y) hx 0, y 0i = 2 3 x 1/3, = 2 3 x2/3 4 5 y4/5 < 0 for all x and y. Therefore (0, 0) is a local max. Note that 2 2 r 2 6 f(x, y) = 49 x 4/ x 6/5 4 5 y 1/5 hx, yi
10 CHAPTER 14. PARTIAL DERIVATIVES 124 Since r 2 f(0, 0) is undefined, we cannot apply the second derivative test. (b) rf(x, y) hx 0, y 0i = 4(x y) 3 + 4(x 1) 3, 4(x y) 3 hx 1, y 1i = 4(x y) 3 + 4(x 1) 3 (x 1) 4(x y) 3 (y 1). Factor out the 4 (and remove it entirely), and then apply the substitution w = x 1 v = y 1 and note that x y = w v (x y) 3 +(x 1) 3 (x 1) (x y) 3 (y 1) = (w v) 3 + w 3 w (w v) 3 v =(w v) 3 w + w 4 (w v) 3 v =(w v) 3 w v + w 4 =(w v) 4 + w 4 > 0 for all w and v. Therefore (1, 1) is a local min. Note that apple r 2 12(x y) (x 1) 2 12(x y) 2 f = 12(x y) 2 12(x y) 2 apple r f(1, 1) = 0 0 Therefore D = 0 and we can t apply the second derivative test.
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Maxima and Minima. Terminology note: Do not confuse the maximum f(a, b) (a number) with the point (a, b) where the maximum occurs.
 10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
MULTI-VARIABLE OPTIMIZATION NOTES. 1. Identifying Critical Points
 MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MATH 105: Midterm #1 Practice Problems
 Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Math 32, October 22 & 27: Maxima & Minima
 Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Lecture 15. Global extrema and Lagrange multipliers. Dan Nichols MATH 233, Spring 2018 University of Massachusetts
 Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Math 233. Extrema of Functions of Two Variables Basics
 Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Math 2411 Calc III Practice Exam 2
 Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
14.6 Directional Derivatives
 CHAPTER 14. PARTIAL DERIVATIVES 107 14.6 Directional Derivatives Comments. Recall that the partial derivatives can be interpreted as the derivatives along traces of f(x, y). We can reinterpret this in
CHAPTER 14. PARTIAL DERIVATIVES 107 14.6 Directional Derivatives Comments. Recall that the partial derivatives can be interpreted as the derivatives along traces of f(x, y). We can reinterpret this in
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables
 Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
14.2 Limits and Continuity
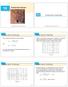 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
CHAPTER 11 PARTIAL DERIVATIVES
 CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
1. Vector Fields. f 1 (x, y, z)i + f 2 (x, y, z)j + f 3 (x, y, z)k.
 HAPTER 14 Vector alculus 1. Vector Fields Definition. A vector field in the plane is a function F(x, y) from R into V, We write F(x, y) = hf 1 (x, y), f (x, y)i = f 1 (x, y)i + f (x, y)j. A vector field
HAPTER 14 Vector alculus 1. Vector Fields Definition. A vector field in the plane is a function F(x, y) from R into V, We write F(x, y) = hf 1 (x, y), f (x, y)i = f 1 (x, y)i + f (x, y)j. A vector field
Math 232. Calculus III Limits and Continuity. Updated: January 13, 2016 Calculus III Section 14.2
 Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
Review guide for midterm 2 in Math 233 March 30, 2009
 Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
MATH Exam 2 Solutions November 16, 2015
 MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
Maxima and Minima. Chapter Local and Global extrema. 5.2 Continuous functions on closed and bounded sets Definition of global extrema
 Chapter 5 Maxima and Minima In first semester calculus we learned how to find the maximal and minimal values of a function y = f(x) of one variable. The basic method is as follows: assuming the independent
Chapter 5 Maxima and Minima In first semester calculus we learned how to find the maximal and minimal values of a function y = f(x) of one variable. The basic method is as follows: assuming the independent
[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and
![[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and [f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and](/thumbs/92/108353356.jpg) Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
11.2 LIMITS AND CONTINUITY
 11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
Functions of several variables
 Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
MATH 234 THIRD SEMESTER CALCULUS
 MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
ANSWER KEY. (a) For each of the following partials derivatives, use the contour plot to decide whether they are positive, negative, or zero.
 Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
LECTURE 19 - LAGRANGE MULTIPLIERS
 LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Partial Differentiation 1 Introduction
 Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Name: ID: Section: Math 233 Exam 2. Page 1. This exam has 17 questions:
 Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
Exam 2 Review Sheet. r(t) = x(t), y(t), z(t)
 Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A
 Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
Test Yourself. 11. The angle in degrees between u and w. 12. A vector parallel to v, but of length 2.
 Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
4 The Cartesian Coordinate System- Pictures of Equations
 The Cartesian Coordinate System- Pictures of Equations Concepts: The Cartesian Coordinate System Graphs of Equations in Two Variables x-intercepts and y-intercepts Distance in Two Dimensions and the Pythagorean
The Cartesian Coordinate System- Pictures of Equations Concepts: The Cartesian Coordinate System Graphs of Equations in Two Variables x-intercepts and y-intercepts Distance in Two Dimensions and the Pythagorean
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Solutions to the problems from Written assignment 2 Math 222 Winter 2015
 Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
INTEGRATION OVER NON-RECTANGULAR REGIONS. Contents 1. A slightly more general form of Fubini s Theorem
 INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
4 to find the dimensions of the rectangle that have the maximum area. 2y A =?? f(x, y) = (2x)(2y) = 4xy
 Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
Honors Algebra 2 Assignment Sheet - Chapter 1
 Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
Calculus 3 Exam 2 31 October 2017
 Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Math 2321 Review for Test 2 Fall 11
 Math 2321 Review for Test 2 Fall 11 The test will cover chapter 15 and sections 16.1-16.5 of chapter 16. These review sheets consist of problems similar to ones that could appear on the test. Some problems
Math 2321 Review for Test 2 Fall 11 The test will cover chapter 15 and sections 16.1-16.5 of chapter 16. These review sheets consist of problems similar to ones that could appear on the test. Some problems
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers
 SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
Unit 7 Partial Derivatives and Optimization
 Unit 7 Partial Derivatives and Optimization We have learned some important applications of the ordinary derivative in finding maxima and minima. We now move on to a topic called partial derivatives which
Unit 7 Partial Derivatives and Optimization We have learned some important applications of the ordinary derivative in finding maxima and minima. We now move on to a topic called partial derivatives which
SOLUTIONS 2. PRACTICE EXAM 2. HOURLY. Problem 1) TF questions (20 points) Circle the correct letter. No justifications are needed.
 SOLUIONS 2. PRACICE EXAM 2. HOURLY Math 21a, S03 Problem 1) questions (20 points) Circle the correct letter. No justifications are needed. A function f(x, y) on the plane for which the absolute minimum
SOLUIONS 2. PRACICE EXAM 2. HOURLY Math 21a, S03 Problem 1) questions (20 points) Circle the correct letter. No justifications are needed. A function f(x, y) on the plane for which the absolute minimum
Math 5BI: Problem Set 1 Linearizing functions of several variables
 Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Review Sheet for Math 230, Midterm exam 2. Fall 2006
 Review Sheet for Math 230, Midterm exam 2. Fall 2006 October 31, 2006 The second midterm exam will take place: Monday, November 13, from 8:15 to 9:30 pm. It will cover chapter 15 and sections 16.1 16.4,
Review Sheet for Math 230, Midterm exam 2. Fall 2006 October 31, 2006 The second midterm exam will take place: Monday, November 13, from 8:15 to 9:30 pm. It will cover chapter 15 and sections 16.1 16.4,
1 Write a Function in
 www.ck12.org Chapter 1. Write a Function in Slope-Intercept Form CHAPTER 1 Write a Function in Slope-Intercept Form Here you ll learn how to write the slope-intercept form of linear functions and how to
www.ck12.org Chapter 1. Write a Function in Slope-Intercept Form CHAPTER 1 Write a Function in Slope-Intercept Form Here you ll learn how to write the slope-intercept form of linear functions and how to
18.3. Stationary Points. Introduction. Prerequisites. Learning Outcomes
 Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Free extrema of two variables functions
 Free extrema of two variables functions Apellidos, Nombre: Departamento: Centro: Alicia Herrero Debón (aherrero@mat.upv.es) Departamento de Matemática Aplicada Instituto de Matemática Multidisciplnar Escuela
Free extrema of two variables functions Apellidos, Nombre: Departamento: Centro: Alicia Herrero Debón (aherrero@mat.upv.es) Departamento de Matemática Aplicada Instituto de Matemática Multidisciplnar Escuela
VECTOR CALCULUS Julian.O 2016
 VETO ALULUS Julian.O 2016 Vector alculus Lecture 3: Double Integrals Green s Theorem Divergence of a Vector Field Double Integrals: Double integrals are used to integrate two-variable functions f(x, y)
VETO ALULUS Julian.O 2016 Vector alculus Lecture 3: Double Integrals Green s Theorem Divergence of a Vector Field Double Integrals: Double integrals are used to integrate two-variable functions f(x, y)
Limits and Continuity
 Limits and Continuity February 26, 205 Previously, you learned about the concept of the it of a function, and an associated concept, continuity. These concepts can be generalised to functions of several
Limits and Continuity February 26, 205 Previously, you learned about the concept of the it of a function, and an associated concept, continuity. These concepts can be generalised to functions of several
Math Lecture 2 Inverse Functions & Logarithms
 Math 1060 Lecture 2 Inverse Functions & Logarithms Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms
Math 1060 Lecture 2 Inverse Functions & Logarithms Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms
Goals: To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
 Unit #23 : Lagrange Multipliers Goals: To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition). Constrained Optimization - Examples
Unit #23 : Lagrange Multipliers Goals: To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition). Constrained Optimization - Examples
 There is another online survey for those of you (freshman) who took the ALEKS placement test before the semester. Please follow the link at the Math 165 web-page, or just go to: https://illinois.edu/sb/sec/2457922
There is another online survey for those of you (freshman) who took the ALEKS placement test before the semester. Please follow the link at the Math 165 web-page, or just go to: https://illinois.edu/sb/sec/2457922
LINEAR EQUATIONS IN TWO VARIABLES
 LINEAR EQUATIONS IN TWO VARIABLES What You Should Learn Use slope to graph linear equations in two " variables. Find the slope of a line given two points on the line. Write linear equations in two variables.
LINEAR EQUATIONS IN TWO VARIABLES What You Should Learn Use slope to graph linear equations in two " variables. Find the slope of a line given two points on the line. Write linear equations in two variables.
47. Conservative Vector Fields
 47. onservative Vector Fields Given a function z = φ(x, y), its gradient is φ = φ x, φ y. Thus, φ is a gradient (or conservative) vector field, and the function φ is called a potential function. Suppose
47. onservative Vector Fields Given a function z = φ(x, y), its gradient is φ = φ x, φ y. Thus, φ is a gradient (or conservative) vector field, and the function φ is called a potential function. Suppose
Lecture 19. Vector fields. Dan Nichols MATH 233, Spring 2018 University of Massachusetts. April 10, 2018.
 Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Logarithmic Functions and Their Graphs
 Logarithmic Functions and Their Graphs Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus Logarithmic Functions and Their Graphs Mr. Niedert 1 / 24 Logarithmic Functions and Their Graphs 1 Logarithmic
Logarithmic Functions and Their Graphs Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus Logarithmic Functions and Their Graphs Mr. Niedert 1 / 24 Logarithmic Functions and Their Graphs 1 Logarithmic
MthSc 103 Test #1 Spring 2011 Version A JIT , 1.8, , , , 8.1, 11.1 ANSWER KEY AND CUID: GRADING GUIDELINES
 Student s Printed Name: ANSWER KEY AND CUID: GRADING GUIDELINES Instructor: Section # : You are not permitted to use a calculator on any portion of this test. You are not allowed to use any textbook, notes,
Student s Printed Name: ANSWER KEY AND CUID: GRADING GUIDELINES Instructor: Section # : You are not permitted to use a calculator on any portion of this test. You are not allowed to use any textbook, notes,
PREREQUISITE/PRE-CALCULUS REVIEW
 PREREQUISITE/PRE-CALCULUS REVIEW Introduction This review sheet is a summary of most of the main topics that you should already be familiar with from your pre-calculus and trigonometry course(s), and which
PREREQUISITE/PRE-CALCULUS REVIEW Introduction This review sheet is a summary of most of the main topics that you should already be familiar with from your pre-calculus and trigonometry course(s), and which
Section 15.3 Partial Derivatives
 Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
JMG. Review Module 1 Lessons 1-20 for Mid-Module. Prepare for Endof-Unit Assessment. Assessment. Module 1. End-of-Unit Assessment.
 Lesson Plans Lesson Plan WEEK 161 December 5- December 9 Subject to change 2016-2017 Mrs. Whitman 1 st 2 nd Period 3 rd Period 4 th Period 5 th Period 6 th Period H S Mathematics Period Prep Geometry Math
Lesson Plans Lesson Plan WEEK 161 December 5- December 9 Subject to change 2016-2017 Mrs. Whitman 1 st 2 nd Period 3 rd Period 4 th Period 5 th Period 6 th Period H S Mathematics Period Prep Geometry Math
5.5 Properties of Logarithms. Work with the Properties of Logarithms. 296 CHAPTER 5 Exponential and Logarithmic Functions
 296 CHAPTER 5 Exponential and Logarithmic Functions The Richter Scale Problems 3 and 32 use the following discussion: The Richter scale is one way of converting seismographic readings into numbers that
296 CHAPTER 5 Exponential and Logarithmic Functions The Richter Scale Problems 3 and 32 use the following discussion: The Richter scale is one way of converting seismographic readings into numbers that
I II III IV V VI VII VIII IX X Total
 1 of 16 HAND IN Answers recorded on exam paper. DEPARTMENT OF MATHEMATICS AND STATISTICS QUEEN S UNIVERSITY AT KINGSTON MATH 121/124 - APR 2018 Section 700 - CDS Students ONLY Instructor: A. Ableson INSTRUCTIONS:
1 of 16 HAND IN Answers recorded on exam paper. DEPARTMENT OF MATHEMATICS AND STATISTICS QUEEN S UNIVERSITY AT KINGSTON MATH 121/124 - APR 2018 Section 700 - CDS Students ONLY Instructor: A. Ableson INSTRUCTIONS:
Practice Problems: Calculus in Polar Coordinates
 Practice Problems: Calculus in Polar Coordinates Answers. For these problems, I want to convert from polar form parametrized Cartesian form, then differentiate and take the ratio y over x to get the slope,
Practice Problems: Calculus in Polar Coordinates Answers. For these problems, I want to convert from polar form parametrized Cartesian form, then differentiate and take the ratio y over x to get the slope,
Chapter 6: Periodic Functions
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
MATH 261 EXAM II PRACTICE PROBLEMS
 MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
Section 7.2 Logarithmic Functions
 Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Pre-AP Algebra 2 Unit 8 - Lesson 2 Graphing rational functions by plugging in numbers; feature analysis
 Pre-AP Algebra 2 Unit 8 - Lesson 2 Graphing rational functions by plugging in numbers; feature analysis Objectives: Students will be able to: Analyze the features of a rational function: determine domain,
Pre-AP Algebra 2 Unit 8 - Lesson 2 Graphing rational functions by plugging in numbers; feature analysis Objectives: Students will be able to: Analyze the features of a rational function: determine domain,
WESI 205 Workbook. 1 Review. 2 Graphing in 3D
 1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
7.3 The Unit Circle Finding Trig Functions Using The Unit Circle Defining Sine and Cosine Functions from the Unit Circle
 7.3 The Unit Circle Finding Trig Functions Using The Unit Circle For any angle t, we can label the intersection of the terminal side and the unit circle as by its coordinates,(x,y).the coordinates x and
7.3 The Unit Circle Finding Trig Functions Using The Unit Circle For any angle t, we can label the intersection of the terminal side and the unit circle as by its coordinates,(x,y).the coordinates x and
10 GRAPHING LINEAR EQUATIONS
 0 GRAPHING LINEAR EQUATIONS We now expand our discussion of the single-variable equation to the linear equation in two variables, x and y. Some examples of linear equations are x+ y = 0, y = 3 x, x= 4,
0 GRAPHING LINEAR EQUATIONS We now expand our discussion of the single-variable equation to the linear equation in two variables, x and y. Some examples of linear equations are x+ y = 0, y = 3 x, x= 4,
MAT187H1F Lec0101 Burbulla
 Spring 17 What Is A Parametric Curve? y P(x, y) x 1. Let a point P on a curve have Cartesian coordinates (x, y). We can think of the curve as being traced out as the point P moves along it. 3. In this
Spring 17 What Is A Parametric Curve? y P(x, y) x 1. Let a point P on a curve have Cartesian coordinates (x, y). We can think of the curve as being traced out as the point P moves along it. 3. In this
MATH Review Exam II 03/06/11
 MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
Mathematics 205 HWK 19b Solutions Section 16.2 p750. (x 2 y) dy dx. 2x 2 3
 Mathematics 5 HWK 9b Solutions Section 6. p75 Problem, 6., p75. Evaluate (x y) dy dx. Solution. (x y) dy dx x ( ) y dy dx [ x x dx ] [ ] y x dx Problem 9, 6., p75. For the region as shown, write f da as
Mathematics 5 HWK 9b Solutions Section 6. p75 Problem, 6., p75. Evaluate (x y) dy dx. Solution. (x y) dy dx x ( ) y dy dx [ x x dx ] [ ] y x dx Problem 9, 6., p75. For the region as shown, write f da as
Chapter 16. Partial Derivatives
 Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
11/1/2017 Second Hourly Practice 2 Math 21a, Fall Name:
 11/1/217 Second Hourly Practice 2 Math 21a, Fall 217 Name: MWF 9 Jameel Al-Aidroos MWF 9 Dennis Tseng MWF 1 Yu-Wei Fan MWF 1 Koji Shimizu MWF 11 Oliver Knill MWF 11 Chenglong Yu MWF 12 Stepan Paul TTH
11/1/217 Second Hourly Practice 2 Math 21a, Fall 217 Name: MWF 9 Jameel Al-Aidroos MWF 9 Dennis Tseng MWF 1 Yu-Wei Fan MWF 1 Koji Shimizu MWF 11 Oliver Knill MWF 11 Chenglong Yu MWF 12 Stepan Paul TTH
Modular Arithmetic. Kieran Cooney - February 18, 2016
 Modular Arithmetic Kieran Cooney - kieran.cooney@hotmail.com February 18, 2016 Sums and products in modular arithmetic Almost all of elementary number theory follows from one very basic theorem: Theorem.
Modular Arithmetic Kieran Cooney - kieran.cooney@hotmail.com February 18, 2016 Sums and products in modular arithmetic Almost all of elementary number theory follows from one very basic theorem: Theorem.
UNIT 2: FACTOR QUADRATIC EXPRESSIONS. By the end of this unit, I will be able to:
 UNIT 2: FACTOR QUADRATIC EXPRESSIONS UNIT 2 By the end of this unit, I will be able to: o Represent situations using quadratic expressions in one variable o Expand and simplify quadratic expressions in
UNIT 2: FACTOR QUADRATIC EXPRESSIONS UNIT 2 By the end of this unit, I will be able to: o Represent situations using quadratic expressions in one variable o Expand and simplify quadratic expressions in
Game Theory. Chapter 2 Solution Methods for Matrix Games. Instructor: Chih-Wen Chang. Chih-Wen NCKU. Game Theory, Ch2 1
 Game Theory Chapter 2 Solution Methods for Matrix Games Instructor: Chih-Wen Chang Chih-Wen Chang @ NCKU Game Theory, Ch2 1 Contents 2.1 Solution of some special games 2.2 Invertible matrix games 2.3 Symmetric
Game Theory Chapter 2 Solution Methods for Matrix Games Instructor: Chih-Wen Chang Chih-Wen Chang @ NCKU Game Theory, Ch2 1 Contents 2.1 Solution of some special games 2.2 Invertible matrix games 2.3 Symmetric
18 Logarithmic Functions
 18 Logarithmic Functions Concepts: Logarithms (Section 3.3) Logarithms as Functions Logarithms as Exponent Pickers Inverse Relationship between Logarithmic and Exponential Functions. The Common Logarithm
18 Logarithmic Functions Concepts: Logarithms (Section 3.3) Logarithms as Functions Logarithms as Exponent Pickers Inverse Relationship between Logarithmic and Exponential Functions. The Common Logarithm
Intercepts and Rapidly Graphing Lines
 Module 1.3 Page 118 of 1390. Module 1.3: Intercepts and Rapidly Graphing Lines This module will review the techniques of rapidly graphing a line on a coordinate plane. By graphing I of course mean physically
Module 1.3 Page 118 of 1390. Module 1.3: Intercepts and Rapidly Graphing Lines This module will review the techniques of rapidly graphing a line on a coordinate plane. By graphing I of course mean physically
Permutation Groups. Every permutation can be written as a product of disjoint cycles. This factorization is unique up to the order of the factors.
 Permutation Groups 5-9-2013 A permutation of a set X is a bijective function σ : X X The set of permutations S X of a set X forms a group under function composition The group of permutations of {1,2,,n}
Permutation Groups 5-9-2013 A permutation of a set X is a bijective function σ : X X The set of permutations S X of a set X forms a group under function composition The group of permutations of {1,2,,n}
Functions: Transformations and Graphs
 Paper Reference(s) 6663/01 Edexcel GCE Core Mathematics C1 Advanced Subsidiary Functions: Transformations and Graphs Calculators may NOT be used for these questions. Information for Candidates A booklet
Paper Reference(s) 6663/01 Edexcel GCE Core Mathematics C1 Advanced Subsidiary Functions: Transformations and Graphs Calculators may NOT be used for these questions. Information for Candidates A booklet
Contents. 1 Matlab basics How to start/exit Matlab Changing directory Matlab help... 2
 Contents 1 Matlab basics 2 1.1 How to start/exit Matlab............................ 2 1.2 Changing directory............................... 2 1.3 Matlab help................................... 2 2 Symbolic
Contents 1 Matlab basics 2 1.1 How to start/exit Matlab............................ 2 1.2 Changing directory............................... 2 1.3 Matlab help................................... 2 2 Symbolic
LECTURE 7: POLYNOMIAL CONGRUENCES TO PRIME POWER MODULI
 LECTURE 7: POLYNOMIAL CONGRUENCES TO PRIME POWER MODULI 1. Hensel Lemma for nonsingular solutions Although there is no analogue of Lagrange s Theorem for prime power moduli, there is an algorithm for determining
LECTURE 7: POLYNOMIAL CONGRUENCES TO PRIME POWER MODULI 1. Hensel Lemma for nonsingular solutions Although there is no analogue of Lagrange s Theorem for prime power moduli, there is an algorithm for determining
MATH 20C: FUNDAMENTALS OF CALCULUS II FINAL EXAM
 MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Trigonometry Final Exam Study Guide Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The graph of a polar equation is given. Select the polar
Trigonometry Final Exam Study Guide Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The graph of a polar equation is given. Select the polar
1.6 Congruence Modulo m
 1.6 Congruence Modulo m 47 5. Let a, b 2 N and p be a prime. Prove for all natural numbers n 1, if p n (ab) and p - a, then p n b. 6. In the proof of Theorem 1.5.6 it was stated that if n is a prime number
1.6 Congruence Modulo m 47 5. Let a, b 2 N and p be a prime. Prove for all natural numbers n 1, if p n (ab) and p - a, then p n b. 6. In the proof of Theorem 1.5.6 it was stated that if n is a prime number
Calculus II Fall 2014
 Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
33. Riemann Summation over Rectangular Regions
 . iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
. iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
Chapter 9 Linear equations/graphing. 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane
 Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
Sect 4.5 Inequalities Involving Quadratic Function
 71 Sect 4. Inequalities Involving Quadratic Function Objective #0: Solving Inequalities using a graph Use the graph to the right to find the following: Ex. 1 a) Find the intervals where f(x) > 0. b) Find
71 Sect 4. Inequalities Involving Quadratic Function Objective #0: Solving Inequalities using a graph Use the graph to the right to find the following: Ex. 1 a) Find the intervals where f(x) > 0. b) Find
5.3 Trigonometric Graphs. Copyright Cengage Learning. All rights reserved.
 5.3 Trigonometric Graphs Copyright Cengage Learning. All rights reserved. Objectives Graphs of Sine and Cosine Graphs of Transformations of Sine and Cosine Using Graphing Devices to Graph Trigonometric
5.3 Trigonometric Graphs Copyright Cengage Learning. All rights reserved. Objectives Graphs of Sine and Cosine Graphs of Transformations of Sine and Cosine Using Graphing Devices to Graph Trigonometric
M.Tolotti - Mathematics (Preparatory) - September Exercises. Maximize p(g(x))g(x) q x subject to x R +
 M.Tolotti - Mathematics (Preparatory) - September 2010 1 Exercises EXERCISE 1. where Maximize p(g(x))g(x) q x subject to x R + p : R R is constant, i.e. p(g(x)) = p = 1 for all x. g(x) = 35x x 2. q = 10.
M.Tolotti - Mathematics (Preparatory) - September 2010 1 Exercises EXERCISE 1. where Maximize p(g(x))g(x) q x subject to x R + p : R R is constant, i.e. p(g(x)) = p = 1 for all x. g(x) = 35x x 2. q = 10.
Kettering University 14 th Mathematics Olympiad. November 22, Problems and Solutions
 Kettering University 14 th Mathematics Olympiad November, 014 Problems and Solutions Problem 1. Solve the equation x x cos y + 1.5 = 0. Solution. x x cos y + 1.5 = x x + 0.5 + 1 cos y = (x 0.5) + (1 cos
Kettering University 14 th Mathematics Olympiad November, 014 Problems and Solutions Problem 1. Solve the equation x x cos y + 1.5 = 0. Solution. x x cos y + 1.5 = x x + 0.5 + 1 cos y = (x 0.5) + (1 cos
1. Measure angle in degrees and radians 2. Find coterminal angles 3. Determine the arc length of a circle
 Pre- Calculus Mathematics 12 5.1 Trigonometric Functions Goal: 1. Measure angle in degrees and radians 2. Find coterminal angles 3. Determine the arc length of a circle Measuring Angles: Angles in Standard
Pre- Calculus Mathematics 12 5.1 Trigonometric Functions Goal: 1. Measure angle in degrees and radians 2. Find coterminal angles 3. Determine the arc length of a circle Measuring Angles: Angles in Standard
6.1 - Introduction to Periodic Functions
 6.1 - Introduction to Periodic Functions Periodic Functions: Period, Midline, and Amplitude In general: A function f is periodic if its values repeat at regular intervals. Graphically, this means that
6.1 - Introduction to Periodic Functions Periodic Functions: Period, Midline, and Amplitude In general: A function f is periodic if its values repeat at regular intervals. Graphically, this means that
