Math Lecture 2 Inverse Functions & Logarithms
|
|
|
- Milo Briggs
- 6 years ago
- Views:
Transcription
1 Math 1060 Lecture 2 Inverse Functions & Logarithms
2 Outline Summary of last lecture Inverse Functions Domain, codomain, and range One-to-one functions Inverse functions Inverse trig functions Logarithms Definition Properties The natural log
3 Summary of last lecture Described coordinated courses, exams, homeworks, quizzes, and grading. Defined four common sets of numbers: N (the natural numbers), Z (the integers), Q (the rational numbers), and R (the real numbers). Described exponential functions, working our way up from a n when n N through a x when x R. Described the graphs of the functions a x and a x, and noticed some commonalities in these graphs. Defined the number e as the unique number so that the tangent line to the graph y = e x at (0, 1) has slope 1. Homework Due Monday: Read Ch. 1 of Stewart, do problems 1.5: 2, 4, 7, 15 and 1.6: 5-8, 29, 30.
4 Domain and codomain Recall that a function is a rule for associating a single output in a set C to each input in a set D. (This is the vertical line test.) The set D is called the domain of the function, and the set C is called the codomain of the function. To denote that f is a function with domain D and codomain C we write f : D C.
5 Example The greatest integer function, denoted [[x]], returns the larger integer less than or equal to x. For instance [[2.34]] = 2, and [[ 3.78]] = 4. The domain of this function is R, but because we can only ever hope to get integers out of the function, the codomain is Z.
6 Examples Function Domain Codomain Notation f (x) = [[x]] R Z f : R Z g(x) = x 2 R R g : R R h(x) = x [0, ) R h : [0, ) R k(x) = 1 x+2 ( 2, ) R k : ( 2, ) R l(z) = (z + 2) 1 /2 ( 2, ) R l : ( 2, ) R Notice that the function is defined for everything in the domain, but does not necessarily hit every value in the codomain. E.g., g(x) = x 2 is never negative; h(x) = x is also never negative, by convention.
7 A convention The function h(x) = x is always positive, but this is by convention. The square root of x, x, should be the number y such that y 2 = x. If x > 0, then there are always two y values satisfying y 2 = x. For example, if y 2 = 4, then y = ±2.
8 A convention Functions can only have one output value, though, so for x to be a function, we must restrict ourselves to either the positive or negative square roots. By convention, the symbol x will always mean the positive square root. If we want the negative root, we will explicitly write x. Important Observation: x 2 = x.
9 The range of a function The codomain of a function f (x) is the set of all possible outputs of the function. The range of a function f (x) is the set of all values in the codomain that are actually obtained. For example, the range of g(x) = x is [0, ): these are the only values will ever get out of x.
10 The vertical line test The graph of a function f (x) i.e., the set of all (x, y)-pairs satisfying y = f (x) always satisfies the vertical line test because exactly one output is associated with each input. However, the same output could occur multiple times.
11 One-to-one In the event that every value in the range occurs for exactly one input value, we say the function is one-to-one (sometimes denoted 1-1). The graphs of one-to-one functions pass both the vertical and horizontal line test. Example:
12 One-to-one In the event that every value in the range occurs for exactly one input value, we say the function is one-to-one (sometimes denoted 1-1). The graphs of one-to-one functions pass both the vertical and horizontal line test. Example:
13 One-to-one In the event that every value in the range occurs for exactly one input value, we say the function is one-to-one (sometimes denoted 1-1). The graphs of one-to-one functions pass both the vertical and horizontal line test. The graph of a function which is not one-to-one:
14 One-to-one In the event that every value in the range occurs for exactly one input value, we say the function is one-to-one (sometimes denoted 1-1). The graphs of one-to-one functions pass both the vertical and horizontal line test. The graph of a function which is not one-to-one:
15 Inverse functions One-to-one functions are special because they are invertible. That means, if y = f (x), then we can find a function g that satisfies x = g(y). I.e., inverse functions undo one another. Example: If f (x) = 3 x, then g(x) = x 3 is its inverse. E.g., 3 = f ( 27), and 27 = g( 3): f (g( 3)) = 3 and g(f ( 27)) = 27. Example: If f (x) = 3x + 2, then g(x) = x 2 3 is its inverse. E.g., 8 = f (2), and 2 = g(8): f (g(8)) = 8 and g(f (2)) = 2.
16 Inverse functions If f : D C is a one-to-one function with range R, then its inverse is usually denoted f 1 and is a function from R back to D, f 1 : R D. Warning: f 1 does not mean f raised to the 1! It is just a notational convention that means the inverse of f. If you want to actually raise a function to 1, write it as (f (x)) 1.
17 f 1 (x) (f (x)) 1 If f (x) = x 3, then f 1 (x) = 3 x while (f (x)) 1 = x 3. f 1 (x) = 3 x (f (x)) 1 = x 3
18 Inverse functions The defining property of the inverse function f 1 is that it undoes f. More precisely, f 1 is the unique function satisfying the following two equations: f ( f 1 (x) ) = x f 1 (f (x)) = x Another way to say this is that if y = f (x), then x = f 1 (y). The inverse switches the roles of x and y. Notice that the domain of f is the range of f 1, and the domain of f 1 is the range of f.
19 Graphs of inverse functions Since the inverse function switches the role of x and y, there is an easy graphical description of inverse functions: the graph of f 1 is the graph of f but reflected about the line y = x.
20 Graphs of inverse functions Since the inverse function switches the role of x and y, there is an easy graphical description of inverse functions: the graph of f 1 is the graph of f but reflected about the line y = x.
21 Graphs of inverse functions Since the inverse function switches the role of x and y, there is an easy graphical description of inverse functions: the graph of f 1 is the graph of f but reflected about the line y = x.
22 Trying to invert a non-invertible function Notice that if a function f is not one-to-one, then its graph reflected about y = x is not a function! This is another way of thinking about one-to-one and invertible functions: if a graph s reflection around y = x does not pass the vertical line test (i.e., isn t the graph of a function), then the originally function is not one-to-one and so not invertible.
23 Trying to invert a non-invertible function Notice that if a function f is not one-to-one, then its graph reflected about y = x is not a function! This is another way of thinking about one-to-one functions: if a function s reflection around y = x is not a function (i.e., fails the vertical line test).
24 Trying to invert a non-invertible function Notice that if a function f is not one-to-one, then its graph reflected about y = x is not a function! This is another way of thinking about one-to-one functions: if a function s reflection around y = x is not a function (i.e., fails the vertical line test).
25 Inverse functions In most situations you can solve for the inverse function using the following procedure: 1. Write down the equation y = f (x) 2. Solve for x, giving an equation x = [some expression involving y]. 3. Swap x and y to get an equation y = [some expression involving x]. 4. The expression on the right-hand side, involving x s, is the inverse function.
26 Example Example: Calculate the inverse of f (x) = x 3 5. Solution: 1. Write y = f (x): y = x Solve for x: y = x 3 5 = y + 5 = x 3 = 3 y + 5 = x = x = 3 y Swap x and y: 4. The inverse is y = 3 x + 5 f 1 (x) = 3 x + 5.
27 Calculating inverses Why does this procedure work? Keep in mind the defining property for an inverse function is f 1 (f (x)) = x. If y = f (x), we need f 1 (y) = x, which just means we have solved for x: we have x by itself on one side of the equation, and an expression involving y s on the other side. The step where we swap x and y is simply putting the equation into the more familiar y = some function of x notation.
28 Example Example: Calculate the inverse of g(x) = 3x+1 x 2. Solution: 1. Write y = f (x): y = 3x + 1 x Solve for x: y = 3x + 1 x 2 = y(x 2) = 3x + 1 = xy 2y = 3x + 1 = xy 2y 3x = 1 = x(y 3) 2y = 1 = x(y 3) = 1 + 2y = x = 1 + 2y y 3.
29 Example (continued) 3. Swapping the x s and y s, we have that the inverse of g(x) = 3x + 1 x 2 which is g 1 (x) = 1 + 2x x 3.
30 Inverse trig functions Notice that the six trig functions (sin(x), cos(x), tan(x), sec(x), csc(x), and tan(x)) are not one-to-one, and so are not invertible. These functions do become invertible if we restrict their domains so that the graphs pass the horizontal line test. This is easiest to explain by example...
31 Restricting the domain to make sin(x) one-to-one
32 Restricting the domain to make cos(x) one-to-one
33 Domains and ranges of inverse trig functions Function Domain Range arcsin [ 1, 1] [ π /2, π /2] arccos [ 1, 1] [0, π] arctan R ( π /2, π /2) arcsec (, 1] [1, ) [0, π /2) ( π /2, π] arccsc [1, ) (0, π /2] arccot (, ) (0, π)
34 Logarithms If a > 0, then the function f (x) = a x is one-to-one, and so it must have an inverse. Like the trigonometric functions, this inverse does not have a nice, closed form. The inverse of a x is called the logarithm with base a and is denoted log a (x). Note this means the logarithm and exponential satisfy the following two equations: log a (a x ) = x a log a (x) = x. Another way to say the same thing: if y = log a (x), then a y = x. For example, log 2 (32) = 5 because 2 5 = 32. Similarly, log 7 (49) = 2 since 7 2 = 49.
35 Graphs of logarithms The graph of a logarithmic function is easy to determine if you know what the corresponding exponential function looks like. Notice that log a (x) is not defined if x 0! If you see log a (0) or log a ( 3) in one of your answers, then you ve made a mistake somewhere!
36 Properties of exponentials Recall that exponential functions satisfied five important properties: (i) a 0 = 1 (ii) a x a y = a x+y. (iii) ax a = a x y y (iv) (a x ) y = a xy (v) (ab) x = a x b x. Using these properties, we can show that log a (x) must satisfy five similar properties. We will prove the first two in class, and leave the other three as an exercise.
37 Properties of logarithms Theorem For all positive real numbers a > 0 and b > 0, and for every pair of real numbers x and y, the following five properties hold: (i) log a (1) = 0 (ii) log a (xy) = log a (x) + log a (y) ( ) (iii) log x a y = log a (x) log a (y) (iv) log a (x y ) = y log a (x) (v) log b (x) = log a(x) log a (b). We ll show properties (i), (ii) and (v), and leave the others as exercises.
38 Properties of logarithms Property (i): log a (1) = 0. Recall that log a (x) is the inverse of a x. Thus a log a (x) = x. So, a log a (1) = 1, and log a (1) must be the power we can raise a to to get 1. There is only possibility: a 0 = 1, and so log a (1) = 0.
39 Properties of logarithms Property (ii) log a (xy) = log a (x) + log a (y). Using properties of exponents, we know a log a (x)+log a (y) = a log a (x) a log a (y) = xy. Taking log a of both sides of the equation gives the result: a log a (x)+log a (y) = xy = log a (a log a (x)+log a (y)) = log a (xy) = log a (x) + log a (y) = log a (xy).
40 Properties of logarithms Property (v) log b (x) = log a(x) log a (b). We know b log b (x) = x. Taking log a of both sides of the equation tells us log a (b log b (x) ) = log a (x). By property (iv) (which we have not shown; try to prove it on your own), we have log b (x) log a (b) = log a (x). Solving for log b (x) gives the result. Example: log 3 (243) = log 10(243) log 10 (3) = 5
41 The natural log As the function e x comes up all the time in calculus, its inverse, log e (x) comes up all the time as well. For this reason we give log e (x) a special name and some special notation: log e (x) is called the natural logarithm and is denoted ln(x). So, ln(x) and e x satisfy the following two equations: ln (e x ) = x e ln(x) = x.
42 Homework 1. Due Monday, 8/25: Read Ch. 1 of Stewart Stewart 1.5: 2, 4, 7, 15 Stewart 1.6: 5-8, 29, 30
Section 7.2 Logarithmic Functions
 Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
5.4 Transformations and Composition of Functions
 5.4 Transformations and Composition of Functions 1. Vertical Shifts: Suppose we are given y = f(x) and c > 0. (a) To graph y = f(x)+c, shift the graph of y = f(x) up by c. (b) To graph y = f(x) c, shift
5.4 Transformations and Composition of Functions 1. Vertical Shifts: Suppose we are given y = f(x) and c > 0. (a) To graph y = f(x)+c, shift the graph of y = f(x) up by c. (b) To graph y = f(x) c, shift
Logs and Exponentials Higher.notebook February 26, Daily Practice
 Daily Practice 2.2.2015 Daily Practice 3.2.2015 Today we will be learning about exponential functions and logs. Homework due! Need to know for Unit Test 2: Expressions and Functions Adding and subtracng
Daily Practice 2.2.2015 Daily Practice 3.2.2015 Today we will be learning about exponential functions and logs. Homework due! Need to know for Unit Test 2: Expressions and Functions Adding and subtracng
SECTION 1.5: TRIGONOMETRIC FUNCTIONS
 SECTION.5: TRIGONOMETRIC FUNCTIONS The Unit Circle The unit circle is the set of all points in the xy-plane for which x + y =. Def: A radian is a unit for measuring angles other than degrees and is measured
SECTION.5: TRIGONOMETRIC FUNCTIONS The Unit Circle The unit circle is the set of all points in the xy-plane for which x + y =. Def: A radian is a unit for measuring angles other than degrees and is measured
PREREQUISITE/PRE-CALCULUS REVIEW
 PREREQUISITE/PRE-CALCULUS REVIEW Introduction This review sheet is a summary of most of the main topics that you should already be familiar with from your pre-calculus and trigonometry course(s), and which
PREREQUISITE/PRE-CALCULUS REVIEW Introduction This review sheet is a summary of most of the main topics that you should already be familiar with from your pre-calculus and trigonometry course(s), and which
Trigonometry Review Page 1 of 14
 Trigonometry Review Page of 4 Appendix D has a trigonometric review. This material is meant to outline some of the proofs of identities, help you remember the values of the trig functions at special values,
Trigonometry Review Page of 4 Appendix D has a trigonometric review. This material is meant to outline some of the proofs of identities, help you remember the values of the trig functions at special values,
Inverse functions and logarithms
 Inverse unctions and logarithms Recall that a unction is a machine that takes a number rom one set and puts a number o another set. Must be welldeined, meaning the unction is decisive: () always has an
Inverse unctions and logarithms Recall that a unction is a machine that takes a number rom one set and puts a number o another set. Must be welldeined, meaning the unction is decisive: () always has an
Logarithmic Functions and Their Graphs
 Logarithmic Functions and Their Graphs Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus Logarithmic Functions and Their Graphs Mr. Niedert 1 / 24 Logarithmic Functions and Their Graphs 1 Logarithmic
Logarithmic Functions and Their Graphs Accelerated Pre-Calculus Mr. Niedert Accelerated Pre-Calculus Logarithmic Functions and Their Graphs Mr. Niedert 1 / 24 Logarithmic Functions and Their Graphs 1 Logarithmic
S56 (5.1) Logs and Exponentials.notebook October 14, 2016
 1. Daily Practice 21.9.2016 Exponential Functions Today we will be learning about exponential functions. A function of the form y = a x is called an exponential function with the base 'a' where a 0. y
1. Daily Practice 21.9.2016 Exponential Functions Today we will be learning about exponential functions. A function of the form y = a x is called an exponential function with the base 'a' where a 0. y
S56 (5.3) Logs and Exponentials.notebook March 02, 2016
 Daily Practice 22.2.206 Today we will be learning about exponential and logarithmic functions. Homework due tomorrow. Need to know for Unit Test 2: Expressions and Functions Adding and subtracng logs,
Daily Practice 22.2.206 Today we will be learning about exponential and logarithmic functions. Homework due tomorrow. Need to know for Unit Test 2: Expressions and Functions Adding and subtracng logs,
2. Be able to evaluate a trig function at a particular degree measure. Example: cos. again, just use the unit circle!
 Study Guide for PART II of the Fall 18 MAT187 Final Exam NO CALCULATORS are permitted on this part of the Final Exam. This part of the Final exam will consist of 5 multiple choice questions. You will be
Study Guide for PART II of the Fall 18 MAT187 Final Exam NO CALCULATORS are permitted on this part of the Final Exam. This part of the Final exam will consist of 5 multiple choice questions. You will be
Chapter 3, Part 1: Intro to the Trigonometric Functions
 Haberman MTH 11 Section I: The Trigonometric Functions Chapter 3, Part 1: Intro to the Trigonometric Functions In Example 4 in Section I: Chapter, we observed that a circle rotating about its center (i.e.,
Haberman MTH 11 Section I: The Trigonometric Functions Chapter 3, Part 1: Intro to the Trigonometric Functions In Example 4 in Section I: Chapter, we observed that a circle rotating about its center (i.e.,
HW#02 (18 pts): All recommended exercises from JIT (1 pt/problem)
 Spring 2011 MthSc103 Course Calendar Page 1 of 7 January W 12 Syllabus/Course Policies BST Review Th 13 Basic Skills Test F 14 JIT 1.1 1.3: Numbers, Fractions, Parentheses JIT 1.1: 2, 6, 8, 9 JIT 1.2:
Spring 2011 MthSc103 Course Calendar Page 1 of 7 January W 12 Syllabus/Course Policies BST Review Th 13 Basic Skills Test F 14 JIT 1.1 1.3: Numbers, Fractions, Parentheses JIT 1.1: 2, 6, 8, 9 JIT 1.2:
MA10103: Foundation Mathematics I. Lecture Notes Week 3
 MA10103: Foundation Mathematics I Lecture Notes Week 3 Indices/Powers In an expression a n, a is called the base and n is called the index or power or exponent. Multiplication/Division of Powers a 3 a
MA10103: Foundation Mathematics I Lecture Notes Week 3 Indices/Powers In an expression a n, a is called the base and n is called the index or power or exponent. Multiplication/Division of Powers a 3 a
WARM UP. 1. Expand the expression (x 2 + 3) Factor the expression x 2 2x Find the roots of 4x 2 x + 1 by graphing.
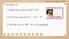 WARM UP Monday, December 8, 2014 1. Expand the expression (x 2 + 3) 2 2. Factor the expression x 2 2x 8 3. Find the roots of 4x 2 x + 1 by graphing. 1 2 3 4 5 6 7 8 9 10 Objectives Distinguish between
WARM UP Monday, December 8, 2014 1. Expand the expression (x 2 + 3) 2 2. Factor the expression x 2 2x 8 3. Find the roots of 4x 2 x + 1 by graphing. 1 2 3 4 5 6 7 8 9 10 Objectives Distinguish between
Graphing Trig Functions. Objectives: Students will be able to graph sine, cosine and tangent functions and translations of these functions.
 Graphing Trig Functions Name: Objectives: Students will be able to graph sine, cosine and tangent functions and translations of these functions. y = sinx (0,) x 0 sinx (,0) (0, ) (,0) /2 3/2 /2 3/2 2 x
Graphing Trig Functions Name: Objectives: Students will be able to graph sine, cosine and tangent functions and translations of these functions. y = sinx (0,) x 0 sinx (,0) (0, ) (,0) /2 3/2 /2 3/2 2 x
18 Logarithmic Functions
 18 Logarithmic Functions Concepts: Logarithms (Section 3.3) Logarithms as Functions Logarithms as Exponent Pickers Inverse Relationship between Logarithmic and Exponential Functions. The Common Logarithm
18 Logarithmic Functions Concepts: Logarithms (Section 3.3) Logarithms as Functions Logarithms as Exponent Pickers Inverse Relationship between Logarithmic and Exponential Functions. The Common Logarithm
Chapter 3 Exponential and Logarithmic Functions
 Chapter 3 Exponential and Logarithmic Functions Section 1 Section 2 Section 3 Section 4 Section 5 Exponential Functions and Their Graphs Logarithmic Functions and Their Graphs Properties of Logarithms
Chapter 3 Exponential and Logarithmic Functions Section 1 Section 2 Section 3 Section 4 Section 5 Exponential Functions and Their Graphs Logarithmic Functions and Their Graphs Properties of Logarithms
MAT01A1. Appendix D: Trigonometry
 MAT01A1 Appendix D: Trigonometry Dr Craig 12 February 2019 Introduction Who: Dr Craig What: Lecturer & course coordinator for MAT01A1 Where: C-Ring 508 acraig@uj.ac.za Web: http://andrewcraigmaths.wordpress.com
MAT01A1 Appendix D: Trigonometry Dr Craig 12 February 2019 Introduction Who: Dr Craig What: Lecturer & course coordinator for MAT01A1 Where: C-Ring 508 acraig@uj.ac.za Web: http://andrewcraigmaths.wordpress.com
Lab I - Direction fields and solution curves
 Lab I - Direction fields and solution curves Richard S. Laugesen September 1, 2009 We consider differential equations having the form In other words, Example 1. a. b. = y, y = f(x, y), = y2 2x + 5. that
Lab I - Direction fields and solution curves Richard S. Laugesen September 1, 2009 We consider differential equations having the form In other words, Example 1. a. b. = y, y = f(x, y), = y2 2x + 5. that
Practice Test 3 (longer than the actual test will be) 1. Solve the following inequalities. Give solutions in interval notation. (Expect 1 or 2.
 MAT 115 Spring 2015 Practice Test 3 (longer than the actual test will be) Part I: No Calculators. Show work. 1. Solve the following inequalities. Give solutions in interval notation. (Expect 1 or 2.) a.
MAT 115 Spring 2015 Practice Test 3 (longer than the actual test will be) Part I: No Calculators. Show work. 1. Solve the following inequalities. Give solutions in interval notation. (Expect 1 or 2.) a.
You could identify a point on the graph of a function as (x,y) or (x, f(x)). You may have only one function value for each x number.
 Function Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second
Function Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second
MAT01A1. Appendix D: Trigonometry
 MAT01A1 Appendix D: Trigonometry Dr Craig 14 February 2017 Introduction Who: Dr Craig What: Lecturer & course coordinator for MAT01A1 Where: C-Ring 508 acraig@uj.ac.za Web: http://andrewcraigmaths.wordpress.com
MAT01A1 Appendix D: Trigonometry Dr Craig 14 February 2017 Introduction Who: Dr Craig What: Lecturer & course coordinator for MAT01A1 Where: C-Ring 508 acraig@uj.ac.za Web: http://andrewcraigmaths.wordpress.com
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Section 7.7 Graphs of the Tangent, Cotangent, Cosecant, and Secant Functions
 Section 7.7 Graphs of the Tangent, Cotangent, Cosecant, and Secant Functions In this section, we will look at the graphs of the other four trigonometric functions. We will start by examining the tangent
Section 7.7 Graphs of the Tangent, Cotangent, Cosecant, and Secant Functions In this section, we will look at the graphs of the other four trigonometric functions. We will start by examining the tangent
Math 147 Section 5.2. Application Example
 Math 147 Section 5.2 Logarithmic Functions Properties of Change of Base Formulas Math 147, Section 5.2 1 Application Example Use a change-of-base formula to evaluate each logarithm. (a) log 3 12 (b) log
Math 147 Section 5.2 Logarithmic Functions Properties of Change of Base Formulas Math 147, Section 5.2 1 Application Example Use a change-of-base formula to evaluate each logarithm. (a) log 3 12 (b) log
6.4 & 6.5 Graphing Trigonometric Functions. The smallest number p with the above property is called the period of the function.
 Math 160 www.timetodare.com Periods of trigonometric functions Definition A function y f ( t) f ( t p) f ( t) 6.4 & 6.5 Graphing Trigonometric Functions = is periodic if there is a positive number p such
Math 160 www.timetodare.com Periods of trigonometric functions Definition A function y f ( t) f ( t p) f ( t) 6.4 & 6.5 Graphing Trigonometric Functions = is periodic if there is a positive number p such
Math 1205 Trigonometry Review
 Math 105 Trigonometry Review We begin with the unit circle. The definition of a unit circle is: x + y =1 where the center is (0, 0) and the radius is 1. An angle of 1 radian is an angle at the center of
Math 105 Trigonometry Review We begin with the unit circle. The definition of a unit circle is: x + y =1 where the center is (0, 0) and the radius is 1. An angle of 1 radian is an angle at the center of
Higher. Expressions & Functions. Unit 2 Course Contents. Higher Higher Higher Higher Higher. Higher Higher. Higher Higher. Higher Higher.
 Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher xpressions & unctions Unit 2 Course Contents Higher
Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher Higher xpressions & unctions Unit 2 Course Contents Higher
Double-Angle, Half-Angle, and Reduction Formulas
 Double-Angle, Half-Angle, and Reduction Formulas By: OpenStaxCollege Bicycle ramps for advanced riders have a steeper incline than those designed for novices. Bicycle ramps made for competition (see [link])
Double-Angle, Half-Angle, and Reduction Formulas By: OpenStaxCollege Bicycle ramps for advanced riders have a steeper incline than those designed for novices. Bicycle ramps made for competition (see [link])
Chapter 6: Periodic Functions
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
Instructor Notes for Chapter 4
 Section 4.1 One to One Functions (Day 1) Instructor Notes for Chapter 4 Understand that an inverse relation undoes the original Understand why the line y = xis a line of symmetry for the graphs of relations
Section 4.1 One to One Functions (Day 1) Instructor Notes for Chapter 4 Understand that an inverse relation undoes the original Understand why the line y = xis a line of symmetry for the graphs of relations
Calculus 3 Exam 2 31 October 2017
 Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Logarithms. Since perhaps it s been a while, calculate a few logarithms just to warm up.
 Logarithms Since perhaps it s been a while, calculate a few logarithms just to warm up. 1. Calculate the following. (a) log 3 (27) = (b) log 9 (27) = (c) log 3 ( 1 9 ) = (d) ln(e 3 ) = (e) log( 100) =
Logarithms Since perhaps it s been a while, calculate a few logarithms just to warm up. 1. Calculate the following. (a) log 3 (27) = (b) log 9 (27) = (c) log 3 ( 1 9 ) = (d) ln(e 3 ) = (e) log( 100) =
Algebra2/Trig Chapter 10 Packet
 Algebra2/Trig Chapter 10 Packet In this unit, students will be able to: Convert angle measures from degrees to radians and radians to degrees. Find the measure of an angle given the lengths of the intercepted
Algebra2/Trig Chapter 10 Packet In this unit, students will be able to: Convert angle measures from degrees to radians and radians to degrees. Find the measure of an angle given the lengths of the intercepted
7.1 INTRODUCTION TO PERIODIC FUNCTIONS
 7.1 INTRODUCTION TO PERIODIC FUNCTIONS Ferris Wheel Height As a Function of Time The London Eye Ferris Wheel measures 450 feet in diameter and turns continuously, completing a single rotation once every
7.1 INTRODUCTION TO PERIODIC FUNCTIONS Ferris Wheel Height As a Function of Time The London Eye Ferris Wheel measures 450 feet in diameter and turns continuously, completing a single rotation once every
Siyavula textbooks: Grade 12 Maths. Collection Editor: Free High School Science Texts Project
 Siyavula textbooks: Grade 12 Maths Collection Editor: Free High School Science Texts Project Siyavula textbooks: Grade 12 Maths Collection Editor: Free High School Science Texts Project Authors: Free
Siyavula textbooks: Grade 12 Maths Collection Editor: Free High School Science Texts Project Siyavula textbooks: Grade 12 Maths Collection Editor: Free High School Science Texts Project Authors: Free
Copyright 2009 Pearson Education, Inc. Slide Section 8.2 and 8.3-1
 8.3-1 Transformation of sine and cosine functions Sections 8.2 and 8.3 Revisit: Page 142; chapter 4 Section 8.2 and 8.3 Graphs of Transformed Sine and Cosine Functions Graph transformations of y = sin
8.3-1 Transformation of sine and cosine functions Sections 8.2 and 8.3 Revisit: Page 142; chapter 4 Section 8.2 and 8.3 Graphs of Transformed Sine and Cosine Functions Graph transformations of y = sin
REVIEW SHEET FOR MIDTERM 2: ADVANCED
 REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
Math 122: Final Exam Review Sheet
 Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
1 Graphs of Sine and Cosine
 1 Graphs of Sine and Cosine Exercise 1 Sketch a graph of y = cos(t). Label the multiples of π 2 and π 4 on your plot, as well as the amplitude and the period of the function. (Feel free to sketch the unit
1 Graphs of Sine and Cosine Exercise 1 Sketch a graph of y = cos(t). Label the multiples of π 2 and π 4 on your plot, as well as the amplitude and the period of the function. (Feel free to sketch the unit
Math 5BI: Problem Set 1 Linearizing functions of several variables
 Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
5.5 Properties of Logarithms. Work with the Properties of Logarithms. 296 CHAPTER 5 Exponential and Logarithmic Functions
 296 CHAPTER 5 Exponential and Logarithmic Functions The Richter Scale Problems 3 and 32 use the following discussion: The Richter scale is one way of converting seismographic readings into numbers that
296 CHAPTER 5 Exponential and Logarithmic Functions The Richter Scale Problems 3 and 32 use the following discussion: The Richter scale is one way of converting seismographic readings into numbers that
Lecture 19. Vector fields. Dan Nichols MATH 233, Spring 2018 University of Massachusetts. April 10, 2018.
 Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Verifying Trigonometric Identities
 25 PART I: Solutions to Odd-Numbered Exercises and Practice Tests a 27. sina =- ==> a = c. sin A = 20 sin 28 ~ 9.39 c B = 90 -A = 62 b cosa=- ==~ b=c.cosa~ 7.66 c 29. a = ~/c 2 - b 2 = -~/2.542-6.22 ~
25 PART I: Solutions to Odd-Numbered Exercises and Practice Tests a 27. sina =- ==> a = c. sin A = 20 sin 28 ~ 9.39 c B = 90 -A = 62 b cosa=- ==~ b=c.cosa~ 7.66 c 29. a = ~/c 2 - b 2 = -~/2.542-6.22 ~
MATH 261 EXAM II PRACTICE PROBLEMS
 MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
Trigonometric Integrals Section 5.7
 A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics Trigonometric Integrals Section 5.7 Dr. John Ehrke Department of Mathematics Spring 2013 Eliminating Powers From Trig Functions
A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics Trigonometric Integrals Section 5.7 Dr. John Ehrke Department of Mathematics Spring 2013 Eliminating Powers From Trig Functions
Differentiable functions (Sec. 14.4)
 Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Math 102 Key Ideas. 1 Chapter 1: Triangle Trigonometry. 1. Consider the following right triangle: c b
 Math 10 Key Ideas 1 Chapter 1: Triangle Trigonometry 1. Consider the following right triangle: A c b B θ C a sin θ = b length of side opposite angle θ = c length of hypotenuse cosθ = a length of side adjacent
Math 10 Key Ideas 1 Chapter 1: Triangle Trigonometry 1. Consider the following right triangle: A c b B θ C a sin θ = b length of side opposite angle θ = c length of hypotenuse cosθ = a length of side adjacent
Math 180 Chapter 6 Lecture Notes. Professor Miguel Ornelas
 Math 180 Chapter 6 Lecture Notes Professor Miguel Ornelas 1 M. Ornelas Math 180 Lecture Notes Section 6.1 Section 6.1 Verifying Trigonometric Identities Verify the identity. a. sin x + cos x cot x = csc
Math 180 Chapter 6 Lecture Notes Professor Miguel Ornelas 1 M. Ornelas Math 180 Lecture Notes Section 6.1 Section 6.1 Verifying Trigonometric Identities Verify the identity. a. sin x + cos x cot x = csc
14.2 Limits and Continuity
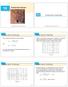 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
7.1 INTRODUCTION TO PERIODIC FUNCTIONS
 7.1 INTRODUCTION TO PERIODIC FUNCTIONS *SECTION: 6.1 DCP List: periodic functions period midline amplitude Pg 247- LECTURE EXAMPLES: Ferris wheel, 14,16,20, eplain 23, 28, 32 *SECTION: 6.2 DCP List: unit
7.1 INTRODUCTION TO PERIODIC FUNCTIONS *SECTION: 6.1 DCP List: periodic functions period midline amplitude Pg 247- LECTURE EXAMPLES: Ferris wheel, 14,16,20, eplain 23, 28, 32 *SECTION: 6.2 DCP List: unit
Chapter 8. Analytic Trigonometry. 8.1 Trigonometric Identities
 Chapter 8. Analytic Trigonometry 8.1 Trigonometric Identities Fundamental Identities Reciprocal Identities: 1 csc = sin sec = 1 cos cot = 1 tan tan = 1 cot tan = sin cos cot = cos sin Pythagorean Identities:
Chapter 8. Analytic Trigonometry 8.1 Trigonometric Identities Fundamental Identities Reciprocal Identities: 1 csc = sin sec = 1 cos cot = 1 tan tan = 1 cot tan = sin cos cot = cos sin Pythagorean Identities:
Functions of more than one variable
 Chapter 3 Functions of more than one variable 3.1 Functions of two variables and their graphs 3.1.1 Definition A function of two variables has two ingredients: a domain and a rule. The domain of the function
Chapter 3 Functions of more than one variable 3.1 Functions of two variables and their graphs 3.1.1 Definition A function of two variables has two ingredients: a domain and a rule. The domain of the function
Section 2.3 Task List
 Summer 2017 Math 108 Section 2.3 67 Section 2.3 Task List Work through each of the following tasks, carefully filling in the following pages in your notebook. Section 2.3 Function Notation and Applications
Summer 2017 Math 108 Section 2.3 67 Section 2.3 Task List Work through each of the following tasks, carefully filling in the following pages in your notebook. Section 2.3 Function Notation and Applications
Algebra 2/Trigonometry Review Sessions 1 & 2: Trigonometry Mega-Session. The Unit Circle
 Algebra /Trigonometry Review Sessions 1 & : Trigonometry Mega-Session Trigonometry (Definition) - The branch of mathematics that deals with the relationships between the sides and the angles of triangles
Algebra /Trigonometry Review Sessions 1 & : Trigonometry Mega-Session Trigonometry (Definition) - The branch of mathematics that deals with the relationships between the sides and the angles of triangles
266&deployment= &UserPass=b3733cde68af274d036da170749a68f6
 Sections 14.6 and 14.7 (1482266) Question 12345678910111213141516171819202122 Due: Thu Oct 21 2010 11:59 PM PDT 1. Question DetailsSCalcET6 14.6.012. [1289020] Find the directional derivative, D u f, of
Sections 14.6 and 14.7 (1482266) Question 12345678910111213141516171819202122 Due: Thu Oct 21 2010 11:59 PM PDT 1. Question DetailsSCalcET6 14.6.012. [1289020] Find the directional derivative, D u f, of
Section 5.2 Graphs of the Sine and Cosine Functions
 A Periodic Function and Its Period Section 5.2 Graphs of the Sine and Cosine Functions A nonconstant function f is said to be periodic if there is a number p > 0 such that f(x + p) = f(x) for all x in
A Periodic Function and Its Period Section 5.2 Graphs of the Sine and Cosine Functions A nonconstant function f is said to be periodic if there is a number p > 0 such that f(x + p) = f(x) for all x in
Exponential and Logarithmic Functions. Copyright Cengage Learning. All rights reserved.
 5 Exponential and Logarithmic Functions Copyright Cengage Learning. All rights reserved. 5.3 Properties of Logarithms Copyright Cengage Learning. All rights reserved. Objectives Use the change-of-base
5 Exponential and Logarithmic Functions Copyright Cengage Learning. All rights reserved. 5.3 Properties of Logarithms Copyright Cengage Learning. All rights reserved. Objectives Use the change-of-base
Example: The graphs of e x, ln(x), x 2 and x 1 2 are shown below. Identify each function s graph.
 Familiar Functions - 1 Transformation of Functions, Exponentials and Loga- Unit #1 : rithms Example: The graphs of e x, ln(x), x 2 and x 1 2 are shown below. Identify each function s graph. Goals: Review
Familiar Functions - 1 Transformation of Functions, Exponentials and Loga- Unit #1 : rithms Example: The graphs of e x, ln(x), x 2 and x 1 2 are shown below. Identify each function s graph. Goals: Review
Trigonometric identities
 Trigonometric identities An identity is an equation that is satisfied by all the values of the variable(s) in the equation. For example, the equation (1 + x) = 1 + x + x is an identity. If you replace
Trigonometric identities An identity is an equation that is satisfied by all the values of the variable(s) in the equation. For example, the equation (1 + x) = 1 + x + x is an identity. If you replace
Honors Algebra 2 Assignment Sheet - Chapter 1
 Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
Review Problems. Calculus IIIA: page 1 of??
 Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
LECTURE 19 - LAGRANGE MULTIPLIERS
 LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
Graphing Sine and Cosine
 The problem with average monthly temperatures on the preview worksheet is an example of a periodic function. Periodic functions are defined on p.254 Periodic functions repeat themselves each period. The
The problem with average monthly temperatures on the preview worksheet is an example of a periodic function. Periodic functions are defined on p.254 Periodic functions repeat themselves each period. The
Section 8.1 Radians and Arc Length
 Section 8. Radians and Arc Length Definition. An angle of radian is defined to be the angle, in the counterclockwise direction, at the center of a unit circle which spans an arc of length. Conversion Factors:
Section 8. Radians and Arc Length Definition. An angle of radian is defined to be the angle, in the counterclockwise direction, at the center of a unit circle which spans an arc of length. Conversion Factors:
Permutation Groups. Every permutation can be written as a product of disjoint cycles. This factorization is unique up to the order of the factors.
 Permutation Groups 5-9-2013 A permutation of a set X is a bijective function σ : X X The set of permutations S X of a set X forms a group under function composition The group of permutations of {1,2,,n}
Permutation Groups 5-9-2013 A permutation of a set X is a bijective function σ : X X The set of permutations S X of a set X forms a group under function composition The group of permutations of {1,2,,n}
2.3 Quick Graphs of Linear Equations
 2.3 Quick Graphs of Linear Equations Algebra III Mr. Niedert Algebra III 2.3 Quick Graphs of Linear Equations Mr. Niedert 1 / 11 Forms of a Line Slope-Intercept Form The slope-intercept form of a linear
2.3 Quick Graphs of Linear Equations Algebra III Mr. Niedert Algebra III 2.3 Quick Graphs of Linear Equations Mr. Niedert 1 / 11 Forms of a Line Slope-Intercept Form The slope-intercept form of a linear
Calculus for the Life Sciences
 Calculus for the Life Sciences Lecture Notes Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego
Calculus for the Life Sciences Lecture Notes Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego
Determine the intercepts of the line and ellipse below: Definition: An intercept is a point of a graph on an axis. Line: x intercept(s)
 Topic 1 1 Intercepts and Lines Definition: An intercept is a point of a graph on an axis. For an equation Involving ordered pairs (x, y): x intercepts (a, 0) y intercepts (0, b) where a and b are real
Topic 1 1 Intercepts and Lines Definition: An intercept is a point of a graph on an axis. For an equation Involving ordered pairs (x, y): x intercepts (a, 0) y intercepts (0, b) where a and b are real
Lecture 3 Presentations and more Great Groups
 Lecture Presentations and more Great Groups From last time: A subset of elements S G with the property that every element of G can be written as a finite product of elements of S and their inverses is
Lecture Presentations and more Great Groups From last time: A subset of elements S G with the property that every element of G can be written as a finite product of elements of S and their inverses is
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Exam 2 Review Sheet. r(t) = x(t), y(t), z(t)
 Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
3.2 Proving Identities
 3.. Proving Identities www.ck.org 3. Proving Identities Learning Objectives Prove identities using several techniques. Working with Trigonometric Identities During the course, you will see complex trigonometric
3.. Proving Identities www.ck.org 3. Proving Identities Learning Objectives Prove identities using several techniques. Working with Trigonometric Identities During the course, you will see complex trigonometric
Section 1.5 An Introduction to Logarithms
 Section. An Introduction to Logarithms So far we ve used the idea exponent Base Result from two points of view. When the base and exponent were given, for instance, we simplified to the result 8. When
Section. An Introduction to Logarithms So far we ve used the idea exponent Base Result from two points of view. When the base and exponent were given, for instance, we simplified to the result 8. When
2.5 Amplitude, Period and Frequency
 2.5 Amplitude, Period and Frequency Learning Objectives Calculate the amplitude and period of a sine or cosine curve. Calculate the frequency of a sine or cosine wave. Graph transformations of sine and
2.5 Amplitude, Period and Frequency Learning Objectives Calculate the amplitude and period of a sine or cosine curve. Calculate the frequency of a sine or cosine wave. Graph transformations of sine and
MATHEMATICAL FUNCTIONS AND GRAPHS
 1 MATHEMATICAL FUNCTIONS AND GRAPHS Objectives Learn how to enter formulae and create and edit graphs. Familiarize yourself with three classes of functions: linear, exponential, and power. Explore effects
1 MATHEMATICAL FUNCTIONS AND GRAPHS Objectives Learn how to enter formulae and create and edit graphs. Familiarize yourself with three classes of functions: linear, exponential, and power. Explore effects
MATH 259 FINAL EXAM. Friday, May 8, Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E
 MATH 259 FINAL EXAM 1 Friday, May 8, 2009. NAME: Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E Instructions: 1. Do not separate the pages of the exam.
MATH 259 FINAL EXAM 1 Friday, May 8, 2009. NAME: Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E Instructions: 1. Do not separate the pages of the exam.
Lesson 1b Linear Equations
 In the first lesson we looked at the concepts and rules of a Function. The first Function that we are going to investigate is the Linear Function. This is a good place to start because with Linear Functions,
In the first lesson we looked at the concepts and rules of a Function. The first Function that we are going to investigate is the Linear Function. This is a good place to start because with Linear Functions,
Chapter 6: Periodic Functions
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
( x "1) 2 = 25, x 3 " 2x 2 + 5x "12 " 0, 2sin" =1.
 Unit Analytical Trigonometry Classwork A) Verifying Trig Identities: Definitions to know: Equality: a statement that is always true. example:, + 7, 6 6, ( + ) 6 +0. Equation: a statement that is conditionally
Unit Analytical Trigonometry Classwork A) Verifying Trig Identities: Definitions to know: Equality: a statement that is always true. example:, + 7, 6 6, ( + ) 6 +0. Equation: a statement that is conditionally
Lesson 8. Diana Pell. Monday, January 27
 Lesson 8 Diana Pell Monday, January 27 Section 5.2: Continued Richter scale is a logarithmic scale used to express the total amount of energy released by an earthquake. The Richter scale gives the magnitude
Lesson 8 Diana Pell Monday, January 27 Section 5.2: Continued Richter scale is a logarithmic scale used to express the total amount of energy released by an earthquake. The Richter scale gives the magnitude
Trigonometry. An Overview of Important Topics
 Trigonometry An Overview of Important Topics 1 Contents Trigonometry An Overview of Important Topics... 4 UNDERSTAND HOW ANGLES ARE MEASURED... 6 Degrees... 7 Radians... 7 Unit Circle... 9 Practice Problems...
Trigonometry An Overview of Important Topics 1 Contents Trigonometry An Overview of Important Topics... 4 UNDERSTAND HOW ANGLES ARE MEASURED... 6 Degrees... 7 Radians... 7 Unit Circle... 9 Practice Problems...
Unit 3 Unit Circle and Trigonometry + Graphs
 HARTFIELD PRECALCULUS UNIT 3 NOTES PAGE 1 Unit 3 Unit Circle and Trigonometry + Graphs (2) The Unit Circle (3) Displacement and Terminal Points (5) Significant t-values Coterminal Values of t (7) Reference
HARTFIELD PRECALCULUS UNIT 3 NOTES PAGE 1 Unit 3 Unit Circle and Trigonometry + Graphs (2) The Unit Circle (3) Displacement and Terminal Points (5) Significant t-values Coterminal Values of t (7) Reference
1111: Linear Algebra I
 1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 7 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 7 1 / 8 Invertible matrices Theorem. 1. An elementary matrix is invertible. 2.
1111: Linear Algebra I Dr. Vladimir Dotsenko (Vlad) Lecture 7 Dr. Vladimir Dotsenko (Vlad) 1111: Linear Algebra I Lecture 7 1 / 8 Invertible matrices Theorem. 1. An elementary matrix is invertible. 2.
Mathematics UNIT FIVE Trigonometry II. Unit. Student Workbook. Lesson 1: Trigonometric Equations Approximate Completion Time: 4 Days
 Mathematics 0- Student Workbook Unit 5 Lesson : Trigonometric Equations Approximate Completion Time: 4 Days Lesson : Trigonometric Identities I Approximate Completion Time: 4 Days Lesson : Trigonometric
Mathematics 0- Student Workbook Unit 5 Lesson : Trigonometric Equations Approximate Completion Time: 4 Days Lesson : Trigonometric Identities I Approximate Completion Time: 4 Days Lesson : Trigonometric
171S5.4p Properties of Logarithmic Functions. November 20, CHAPTER 5: Exponential and Logarithmic Functions. Examples. Express as a product.
 MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 5: Exponential and Logarithmic Functions 5.1 Inverse Functions 5.2 Exponential Functions and Graphs 5.3 Logarithmic Functions
MAT 171 Precalculus Algebra Dr. Claude Moore Cape Fear Community College CHAPTER 5: Exponential and Logarithmic Functions 5.1 Inverse Functions 5.2 Exponential Functions and Graphs 5.3 Logarithmic Functions
Year 10 Term 1 Homework
 Yimin Math Centre Year 10 Term 1 Homework Student Name: Grade: Date: Score: Table of contents 6 Year 10 Term 1 Week 6 Homework 1 6.1 Triangle trigonometry................................... 1 6.1.1 The
Yimin Math Centre Year 10 Term 1 Homework Student Name: Grade: Date: Score: Table of contents 6 Year 10 Term 1 Week 6 Homework 1 6.1 Triangle trigonometry................................... 1 6.1.1 The
5-5 Multiple-Angle and Product-to-Sum Identities
 Find the values of sin 2, cos 2, tan 2 1 cos for the given value interval, (270, 360 ) Since on the interval (270, 360 ), one point on the terminal side of θ has x-coordinate 3 a distance of 5 units from
Find the values of sin 2, cos 2, tan 2 1 cos for the given value interval, (270, 360 ) Since on the interval (270, 360 ), one point on the terminal side of θ has x-coordinate 3 a distance of 5 units from
Number Theory/Cryptography (part 1 of CSC 282)
 Number Theory/Cryptography (part 1 of CSC 282) http://www.cs.rochester.edu/~stefanko/teaching/11cs282 1 Schedule The homework is due Sep 8 Graded homework will be available at noon Sep 9, noon. EXAM #1
Number Theory/Cryptography (part 1 of CSC 282) http://www.cs.rochester.edu/~stefanko/teaching/11cs282 1 Schedule The homework is due Sep 8 Graded homework will be available at noon Sep 9, noon. EXAM #1
Lesson Plan Mr. Baglos Course: Honors Algebra II As of: 4/2/18. After School: 2:30-3:30 Room 2232
 Lesson Plan Mr. Baglos Course: Honors Algebra II As of: 4/2/18 After School: 2:30-3:30 Room 2232 HW: Finish all notes for the day, do the assignment from your HMH workbook, Gizmos, your Math Journal, and
Lesson Plan Mr. Baglos Course: Honors Algebra II As of: 4/2/18 After School: 2:30-3:30 Room 2232 HW: Finish all notes for the day, do the assignment from your HMH workbook, Gizmos, your Math Journal, and
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Review #Final Exam MATH 142-Drost
 Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
# 1,5,9,13,...37 (hw link has all odds)
 February 8, 17 Goals: 1. Recognize trig functions and their integrals.. Learn trig identities useful for integration. 3. Understand which identities work and when. a) identities enable substitution by
February 8, 17 Goals: 1. Recognize trig functions and their integrals.. Learn trig identities useful for integration. 3. Understand which identities work and when. a) identities enable substitution by
2.4 Translating Sine and Cosine Functions
 www.ck1.org Chapter. Graphing Trigonometric Functions.4 Translating Sine and Cosine Functions Learning Objectives Translate sine and cosine functions vertically and horizontally. Identify the vertical
www.ck1.org Chapter. Graphing Trigonometric Functions.4 Translating Sine and Cosine Functions Learning Objectives Translate sine and cosine functions vertically and horizontally. Identify the vertical

 # %
# %