c) How many different four-digit numbers can be formed by arranging the digits 2, 1, 1, and 6?
|
|
|
- Howard Berry
- 6 years ago
- Views:
Transcription
1 Arsenio Says, Show Me The Digits!. a) From the digits 0,,, 3, 4, 5, 6, how many four-digit numbers with distinct digits can be constructed? {0463 is not a four-digit number!} b) Of these, how many are even? c) How many different four-digit numbers can be formed by arranging the digits,,, and 6? Being Wholly Positive About The Number Of Divisors. How many distinct positive whole number divisors are there of the integer {Hint: , so every divisor is uniquely determined by ,000? Number of factors of Number of factors of 3 Number of factors of 5 } Fair-minded Santa. 3. a) In how many ways can 9 different toys be divided evenly among three children? {Hint: The distribution of toys boils down to Which 3 toys for child # Which 3 toys for child # Which 3 toys for child #3 } b) In how many ways can 9 identical toys be divided evenly among three children? Boys Are Icky; No Girls Are Icky. 4. Three boys and 3 girls will sit together in a row. a) How many different ways can they sit together without restrictions? b) How many different ways can they sit together if the genders must sit together? c) How many different ways can they sit together if only the boys must sit together? d) How many different ways can they sit together if no two of the same gender can sit together?
2 You ve Seen One Painting, You ve Seen Them All. 5. An art collection on auction consisted of 4 Dalis, 5 Van Goghs, and 6 Picassos, and at the art auction were 5 art collectors. The society page reporter only observed the number of Dalis, Van Goghs, and Picassos acquired by each collector. a) How many different results could she have recorded for the sale of the Dalis if all were sold? b) How many different results could she have recorded for the sale of the Van Goghs if all were sold? c) How many different results could she have recorded for the sale of the Picassos if all were sold? d) How many different results could she have recorded for the sale of all 5 paintings if all were sold? {Hint: If we assume that each collector buys at least one Picasso then we ll decide how many each collector gets by choosing 4 spaces from the 5 spaces between the 6 Picassos: Collector # gets Picasso Collector # gets Picassos Collector # 3 gets Picasso Collector # 4 gets Picasso Collector # 5 gets Picasso So if each must buy at least one, there are 5 C 4 5 different ways that the 6 Picassos could have been sold to the 5 collectors. To allow for the possibility that one or more collectors didn t buy any Picassos, we ll pretend that there are actually Picassos for the 5 collectors to buy. Collector # gets 3 Picassos Collector # gets Picassos Collector # 3 gets Picasso Collector # 4 gets 3 Picassos Collector # 5 gets Picassos From the 0 spaces available, we ll select 4. If we subtract from each number of Picassos assigned to each collector, we ll have a way that the collectors could buy all 6 Picassos even if some don t buy any. Collector # gets Picassos Collector # gets Picasso Collector # 3 gets 0 Picassos Collector # 4 gets Picassos Collector # 5 gets Picasso }
3 Bob And Carol And Ted And Alice And 6. Three married couples have bought six seats in a row for a performance of a musical comedy. a) In how many different ways can they be seated? b) In how many different ways can they be seated if each couple must sit together with the husband to the left of his wife? c) In how many different ways can they be seated if each couple must sit together? d) In how many different ways can they be seated if all the men must sit together and all the women must sit together? Fancy Dealing. 7. How many different ways can you select 3 cards out of a standard 5 card deck so that the 3 cards selected include at least 3 cards from each suit? {Hint: If you have at least 3 cards of each of the four suits, that gives you cards. You just need one more card.} If you count it using 3C 3 3C 3 3C # of ways to choose 3 hearts # of ways to choose 3 diamonds # of ways to choose 3 spades C 40 # of ways to choose 3 clubs # of ways to choose the 3 th card You will over count. Here s why: Suppose that one time you choose,, and 3 of hearts,,, and 3 of diamonds,,, and 3 of spades,,, and 3 of clubs and your 3 th card is the 4 of hearts, and the next time you choose,, and 4 of hearts,,, and 3 of diamonds,,, and 3 of spades,,, and 3 of clubs and your 3 th card is the 3 of hearts. Then the two selections are the same, but they are counted as two different selections. Instead, try the approach Which suit will have 4 cards? # of ways to choose 4 of this kind # of ways to choose 3 of the next kind # of ways to choose 3 of the next kind # of ways to choose 3 of the last kind
4 Ups and Downs With And Without Nine Lives. 8. a) An elevator starts at the basement with 8 people(not including the elevator operator) and discharges them all by the time it reaches the 6 th floor. In how many ways could the operator record the number of people leaving the elevator on each of the 6 floors? b) If the same elevator also has 0 cats, in how many ways could the operator record the number of cats leaving the elevator on each of the 6 floors? c) In how many ways could the operator record the number of people and the number of cats leaving the elevator on each of the 6 floors? {Hint: See the hint for #5.} Don t Spend It All In One Place. 9. We have $0,000 dollars that must be invested among 4 possible opportunities. Each investment must be a whole number multiple of $,000, and there are minimal investments that must be made. The minimal investments are,, 3, and 4 thousand dollars, respectively. How many different investment strategies are available? {Hint: See the hint for #5.} Hopefully, You ll Have A Lot Of Interest In These Banks. 0. Determine the number of different paths for spelling the word BANK: K N K A N K B A N K {Hint: The letters actually form a tree diagram: B A A N N N N }
5 It s All In The Name.. a) Explain why in a group of 677 people with names spelled from the letters A-Z, at least two people share first and last names beginning with the same letters. For example, the names could be Chris Jones and Charles Jackson. {Hint: How many different ways are there for the beginning letters of a person s first and last names? # of choices for the first letter of the first name # of choices for the first letter of the last name } b) What is the fewest number of people needed to guarantee that at least two people share first, middle, and last names beginning with the same letters?(assume that everyone has first, middle, and last names.) For example, the names could be Chris Allen Jones and Charles Arnold Jackson. c) What is the fewest number of people needed to guarantee that at least three people share first and last names beginning with the same letters? d) What is the fewest number of people needed to guarantee that at least three people share first, middle, and last names beginning with the same letters?(assume that everyone has first, middle, and last names.) It s A Monthly Thing.. a) What is the smallest number of people in a group that will guarantee that at least two of the people were born in the same month? b) What is the smallest number of people in a group that will guarantee that at least three of the people were born in the same month?
6 Texas Hold em. 3. In this problem, we ll determine the number of possible particular 5-card poker hands. Here is a possible decision process for the 5-card poker hand with one pair 3 4C 3 C Which one Which one of the first of the kind? second kind? Which kind of pair? Which two cards of this kind? Which 3 other kinds? Which one of the third kind? So there are 3 4C C ,098,40 different two-of-a-kind 5-card poker hands. a) See if you can do the same thing to find the number of different three-of-a-kind hands: Which kind of three-ofa-kind? Which three cards of this kind? Which other kinds? Which one of the first kind? Which one of the second kind? b) See if you can do the same thing to find the number of different four-of-a-kind hands: Which kind of four-ofa-kind? Which other kinds? Which one of the other kind? The number of different flushes, i.e. five cards of the same suit, but not in order First we ll count the number of different hands with 5 cards of the same suit: 4 3C 5 Which suit? Which 5 cards? Then we ll subtract the number of hands with 5 cards of the same suit that are in order(these would be straight flushes): 4 0 Which kind of card Which suit? starts the straight flush? So we get 4 3C5 40 5,08 different 5-card poker hands which are flushes. c) See if you can do something similar to find the number of straights, i.e. 5 cards in a row, but not all of the same suit. First we ll count the number of different hands with 5 cards in a row: Which kind of card starts the straight? Which suit for the first card? Which suit for the second card? Which suit for the third card? Which suit for the fourth card? Which suit for the fifth card? Then we ll subtract the number of 5-card hands in order of the same suit(straight flushes):
7 Red Or White, It s Your Joyce. 4. To win a math contest, Joyce must determine how many marbles are in a box. She is told that there are 3 identical red marbles and some number of identical white marbles in the box. She is also told that there are 35 distinguishable permutations of the marbles. So how many marbles are in the box? {Hint: The number of distinguishable permutations is RW! R! W!, and we know that R 3.} You have learned that the number of permutations of n distinct objects is n!. For instance if you wanted to seat three people along one side of a rectangular table, the number of possible arrangements is 3!. However, if the three people are to be seated around a circular table, the number of possible arrangements is only!. Let s see why: If the people are labeled A, B, and C, the two arrangements look like the following: A A B C C B At first, it might seem that there should be 3! = 6 different arrangements, like the following: A A B B C C B A C () () (3) B C C C A A (4) (5) (6) But, if you look closely, you ll see that arrangements (), (4), and (5) are identical, each is just a rotation of the other. The same is true of (), (3), and (6). B B A
8 Knights Of The Circular Table And The Venerable Bead. 5. a) Find a formula for the number of different ways that n people(or objects) can be seated(or placed) around a circular table. {Hint: Start with n!, but divide it by the number of rotations that can be made that generate equivalent arrangements.} b) Use the previous formula to find the number of different arrangements of people around a circular table. c) Use the previous formula to find the number of different necklaces that use 0 different colored beads. d) Modify the previous formula to find the number of different necklaces that use 0 beads with 5 red, 4 blue, 8 green, and 3 yellow. {Hint: Similarly modify the formula for permutations of non-distinguishable objects.} Multiples Of Multiples. 6. a) How many of the first,000 counting numbers are multiples of or multiples of 5? {Hint: multiples of or multiples of 5 multiples of multiples of 5 nmultiples of and 5 n n n.} b) How many of the first 0,003 counting numbers are multiples of or multiples of 3?
9 Don t Get Punched Out At The Motel. 7. A national motel chain has replaced the key lock for each room with a key card system. A door is unlocked by inserting a plastic card into a slot above the door knob. Each key s unique identity is determined by a grid of 63 cells, each of which is either solid or punched Room # a) Determine the number of different key cards possible. b) How many are possible if each key card must have at least one punched cell?
10 It s As Easy As ABCDEFG. 8. Find the number of permutations of ABCDEFG that contain the following: a) the sequence ABC {Hint: They would look like one of the following: A B C A B C A B C A B C A B C.} b) the sequences AB, CD, and EF, but not necessarily in this order. {Hint: Treat each pair of letters as a single unit, and decide the position of G. For example, AB CD EF G AB CD G EF AB G CD EF G AB CD EF.} c) the sequences AB, BC, and EF, but not necessarily in this order. Man Have We Got A Lot Of Different Pizzas. 9. A pizza parlor offers four sizes of pizza(small, medium, large, and colossus), two types of crust(thick and thin), and 4 different toppings. a) If you must choose a size, a crust, and at least topping, and you can t duplicate a topping, how many different pizzas can be made? b) How many if double toppings are allowed?
11 Too Many Officers And Not Enough Enlisted. 0. A president, treasurer, and secretary, all different, are to be chosen from a club consisting of 0 people(a, B, C, D, E, F, G, H, I, J). How many different choices of officers are possible if a) there are no restrictions? b) A and B will not serve together? {Hint: Some selections will have only B, some only A, and some won t have either.} 8 7 B is President Treasurer Secretary 8 7 President A is Treasurer Secretary c) C and D will serve together or not at all? {Hint: Some selections will have C and D, and some won t have either.} 8 C is President D is Treasurer Secretary d) E must be an officer? {Hint: E has to be one of the officers selected.} e) F will only serve if she is president? 9 8 President Treasurer E is Secretary {Hint: Some selections will have F as president, and some won t have F as an officer.} 9 8 F is President Treasurer Secretary Even You Can Choose Two.. In how many different ways can you select two distinct integers from the set,,3,,00 so that their sum is even? {Hint: What kinds of numbers will produce even sums? even even?, odd odd?, even odd?}
12 Congratulations Mr. and Mrs. Zeta.. Mr. and Mrs. Zeta want to name their baby so that its monogram(first, middle, and last initials) will be in alphabetical order with no letters repeated. How many such monograms are possible? Shake It Like You Mean It. 3. a) Twenty people are at a party. If everyone at the party shakes the hand of everyone else at the party, determine the total number of handshakes. b) Ten married couples are having a party. If each person at the party shakes the hand of everyone else except his/her spouse, determine the number of handshakes at the party. Don t Lose Your Marbles! 4. An urn contains 5 red, 6 blue, and 8 green marbles. If a set of 3 marbles is randomly selected, without replacement, a) what is the probability that all the marbles will be of the same color? b) what is the probability that the marbles will be of different colors? c) Answer parts a) and b) if each time a marble is selected, its color is recorded and then it s put back into the urn. Imelda Returns. 5. A closet contains 0 pairs of shoes. If 8 shoes are selected, without replacement, how many ways can there be a) no complete pair? Hint: Here are the ten pairs of shoes: LR LR LR 3 3 LR 4 4 LR 5 5 LR 6 6 LR 7 7 LR 8 8 LR 9 9 L0 R 0 0C 8 Which 8 pairs? Shoe from st pair selected Shoe from nd pair selected Shoe from 8 th pair selected b) exactly one complete pair?
13 Bob And Carol And Ted And Alice And The Saga Continues. 6. Six married couples are standing in a room. a) If two people are chosen at random, find the probability that they are married. b) If two people are chosen at random, find the probability that one is male and one is female. c) If four people are chosen at random, find the probability that two married couples are chosen. d) If four people are chosen at random, find the probability that no married couple is chosen. e) If the people are divided into 6 pairs, find the probability that each pair is married. f) If the people are divided into 6 pairs, find the probability that each pair contains a male and a female. It s All Ancient Greek To Me. 7. You have wandered by accident into a class in ancient Greek. A ten-question multiple choice test is handed out, with each answer to be chosen from four possibilities. If you randomly guess the answers, what is the probability that you will get all the answers right? There is an important principle in probability that generalizes the formula P A B P A PB P A B to more than two events, and it s called the Inclusionexclusion Principle. For three events, we can derive it from the formula for two events, A B C A B A C A B A C A B C : assuming that and P A B C P A B C P A P B C P A B C In short, P A P B P C P B C P A B A C P A P B P C P B C P A B P A C P A B C P A B C P A B C P A P B P C P B C P A B P A C.. The pattern in general is to add the single event probabilities, subtract the double event probabilities, add the triple event probabilities,. So for example with four events the formula is
14 PB D PC D PA B C PA B D PA C D PB C D P A B C D P A B C D P A P B P C P D P A B P A C P A D P B C You may use the Inclusion-exclusion Principle in solving the next two problems. I m Missing A Suit, But Don t Call The Dry Cleaner. 8. Find the probability that 3 randomly selected cards from a standard 5 card deck will be missing at least one of the four suits. {Hint: Let C be the event that the 3 cards are missing clubs, D be the event that the 3 cards are missing diamonds, H be the event that the 3 cards are missing hearts, and S be the event that the 3 cards are missing spades. P C D H S P C P D P H P S P C D P C H P C S PD H PD S PH S PC D H PC D S PD H S PC H S PC D H S } The Mad Hat-Checker. 9. A hat-checker in a theater mixed up all five of his checks and decided to hand out all of the hats at random at the end of the show. What is the probability that not a single person received his/her hat back? {Hint: Let A be the event that the first owner gets his hat back, B the event that the second owner gets his hat back, with events C, D, and E defined similarly. The probability that we want to calculate is P A B C D E, so use the Inclusion-exclusion Principle to do it.} Roll The Bones Differently. 30. a) If four fair dice are thrown, what is the probability that the four numbers turning up will all be different? {Hint: Each of the different ways the dice could turn up different would correspond to a permutation of size 4 of the numbers -6.} b) If six fair dice are thrown, then what is the probability that at least one number will repeat?
15 Eleven The Hard Way. 3. a) A fair coin is tossed 4 times, find the probability of tossing at least consecutive tails. {Hint: Here are the different ways of having exactly consecutive tails: T T T T T T T T T T T H H or T H or T H T T T T T T T T T T T H H or T H or T H T T T T T T T T T T T H So you get H or T H or T H T T T T T T T T T T T. Do the same for exactly, exactly 3, and exactly 4.} b) A fair coin is tossed 5 times, find the probability of tossing at least consecutive tails. It s The Length Of The Hypotenuse That Counts. 3. a) If x and y are numbers randomly chosen between 0 and, what is the probability that the hypotenuse of a right triangle with legs of x and y will have length less than? {Hint: y x y x b) Do the same, but for the hypotenuse length being less than. }
16 Where Everybody Knows Your Name. 33. Frasier and Sam both plan to call Diane tonight to ask her for a date. Frasier plans to call between 5:00 PM and 8:00 PM while Sam plans to call between 6:00 PM and 9:00 PM. If they pick their actual calling times at random, what is the probability that Frasier calls before Sam? {Hint: Sam s calling time 9 6 On this line, they call at the same time. 5 8 Frasier s calling time } We re All Winners Here. 34. Three runners compete in a race. The probability that A will win the race is twice the probability that B will win. The probability that B will win is twice the probability that C will win. What is the exact probability that A will win the race?
17 Just Stick To It. 35. a) A box contains 5 sticks measuring 5, 30, 40, 60, and 90 centimeters in length. If three of the sticks are randomly chosen, what is the probability that they can be arranged to form a triangle? {Hint: In order for the three sticks to form a triangle, the length of the longest stick must be less than the sum of the lengths of the other two sticks. Longest stick Medium stick Small stick b) Do the same, but the lengths are 5, 30, 40, 50, and 80. } Another Marble Question Out Of The Blue. 36. A box contains less than 0 marbles. If you randomly select two marbles without replacement, a) you have a 3 box? chance of getting two blue marbles. How many blue marbles are in the b) you have a 50% chance of getting two blue marbles. How many blue marbles are in the box? A Patriotic Marble Problem. 37. A bag contains marbles which are colored red, white, or blue. The probability of drawing a red marble is 6, and the probability of drawing a white marble is 3. a) What is the probability of drawing a blue marble? b) What is the smallest number of marbles that could be in the bag? c) If the bag contains four red marbles and eight white marbles, how many blue marbles does it contain?
18 Hey, What s Your Sign? 38. There are signs of the zodiac. Assuming that a person is just as likely to be born under one sign as another, what is the probability that in a group of 5 people at least two of them a) have the same sign? {Hint: The opposite of at least two have the same sign is that all 5 have different signs.} b) are Aries? Escape from Castle Warwick. 39. You re trapped at Castle Warwick. The only escape is to reach Castle Howard through a system of canals. The problem is that the system of canals has five gatehouses, each run by a cranky gatekeeper who shows up for work about half the time. So the probability that a gate is open on a given day is one-half. The arrows show the way the water flows through the canals and indicate the only direction of travel. What is the probability that a water route from Castle Warwick to Castle Howard is open so that you can escape? Warwick Howard 5 {Hint: There are 3 different states of the five gate houses. Here are the ways you can t get to Castle Howard open or closed open or closed closed closed open or closed closed closed open closed open or closed closed open or closed closed open closed closed closed open open closed }
19 Raiders Of The Lost Arc. 40. A line segment PQ goes across a circle of radius 3. a) Suppose that the shorter distance around the circle from P to Q is. What is the probability that a second line segment drawn at random from P to another point on the circle will be shorter than PQ? P Q Hint: The circumference of the circle is 6. The length of portion of the circumference where we can choose a point R so that PR is shorter than PQ is 4. P Q b) Suppose that the distance around the circle from P to Q is 3. What is the probability that a second line segment drawn at random from P to another point on the circle will be shorter than PQ? I Repeat; Don t Lose Your Marbles! 4. A bowl initially contains 5 white and 7 black marbles. Each time a marble is selected, its color is noted and it is replaced in the bowl along with other marbles of the same color. a) Find the probability that the first two marbles selected are black and the next two white. b) Find the probability that of the first 4 marbles selected, exactly two are black.
20 No Fair, Two Heads Are Better Than One. 4. A gambler has in his pocket a fair coin and a two-headed coin. He selects one of the coins at random; when he flips it, it shows heads. a) What is the probability that it is the fair coin? b) Suppose he flips the same coin a second time and again it shows heads. Now what is the probability that it is the fair coin? c) Suppose he flips the same coin a third time and it show tails. Now what is the probability that it is the fair coin? Why Would Anyone Jump Out Of A Perfectly Good Airplane? 43. A parachutist will jump from an airplane and land in a square field that is kilometers on each side. In each corner of the field there is a group of trees. The parachutist s ropes will get tangled in a tree if he lands within kilometer of a corner. What is the probability that 9 the parachutist will land in the field without getting caught in a tree? {Hint: The parachutist must land inside the gray region of the square. 9 Km Km }
21 No Matter What You Do, You re Gonna Get Tangled Up. 44. Refer to the previous parachute problem. Suppose the parachutist gets caught in a corner tree if he lands within x kilometers of a corner. Find the smallest value of x so that the probability of getting caught is? {Hint: You might think that the answer is picture looks like with this radius: because 4, but here s what the Safe zone Notice the overlap of the tree regions.} For the probability of getting caught in a corner tree to be and x being the smallest, the picture would have to look like this.
22 Bowling For Marbles. 45. Bowl I contains white and 4 red marbles, whereas bowl II contains white and red marble. A marble is randomly chosen from bowl I and transferred into bowl II, and then a marble is randomly selected from bowl II. a) What is the probability that the marble selected from bowl II is white? b) What is the probability that the transferred marble was white, given that a white marble is selected from bowl II? The Worst You Get Is A B. 46. You enter the maze at the start and you choose the paths randomly moving from left to right until you arrive in either room A or room B. 4 5 Start B A a) Find the probability that you end up in room A. b) Find the probability that you end up in room B. c) Find the probability that path 3 was selected given that you ended up in room A. d) Find the probability that path 3 was selected given that you ended up in room B. e) Find the probability that path was selected given that you ended up in room A. {Hint: The maze path is almost a probability tree.}
23 It s All There In Black And White. 47. If two marbles are removed at random without replacement from a bag containing black and white marbles, the probability that they are both white is. If three are removed at random 3 without replacement, the probability that they are all white is. How many marbles of 6 each color are in the bag? W W {Hint: W B W B 3 W W W and. Substitute the first W B W B W B 6 equation into the second one, and then substitute the result back into the first equation.} Kermit Asked: What s On The Other Side? 48. Three cards - one is red on both sides, another is black on both sides, and the other is red on one side and black on the other side are placed into a hat. You randomly pull out one card and look at just one side of it. It is red. What is the probability that the card you hold is red on both sides? {Hint: An equally likely sample space for this experiment is S r, r, r, r, b, b, b, b, r, b, b, r, where each ordered pair card card card 3 represents what color is on the one side you look at and what color is on the other side.} How Fair Is The Fair? 49. At a state fair a game is played by tossing a coin of radius 0 millimeters onto a large table ruled into congruent squares each with side measure of 5 millimeters. If the coin lands entirely within some square, the player wins a prize. If the coin touches or crosses the edge of any square, the player loses. Assuming that the coin lands somewhere on the table, what s the probability that the player wins? {Hint: The center of the coin must land inside the gray region of the square. 0 mm 5 mm }
24 Let s At Least Make It Refer to the previous problem. What should be the radius of the coin so that the probability of winning is.5? You re Just Throwing Darts. 5. If a dart hits the square target at random, what is the probability that it will hit in a shaded region? 6 cm cm 4 cm {Hint: Think about area.} 8 cm Will It Be A Man Or A Woman? 5. One student in a class of men and women is to be chosen to represent the class. Each student is equally likely to be chosen, and the probability that a man is chosen is 3 the probability that a woman is chosen. What is the ratio of the number of men to the total number of men and women? M 3W {Hint: M W M W of the equation.} which implies that M W 3, so substitute this into the right side
25 Oh, The French. 53. The French nobleman Antoine Gombauld, the Chevalier de Mere, was a famous 7 th - century gambler. He loved dice games. One of his favorites was betting that a 6 would appear at least once in four rolls of a die. He eventually became bored with this game, and came up with a new one. In the new game, he bet that there would be at least one pair of 6 s in 4 rolls of a pair of dice. He soon noticed that he was not winning as much with the new game. In 654, Gombauld wrote a letter to the French mathematician Blaise Pascal, who in turn mentioned the problem to Pierre de Fermat. The two mathematicians solved the mystery. See if you can too by working out the following parts. This exchange between gambler and mathematician is said to be the birth of the study of probability. In a letter to Fermat referring to Gombauld, Pascal wrote: He is very intelligent, but he is not a mathematician: this as you know is a great defect. a) Find the probability of getting at least one 6 in four rolls of a fair die. {Hint: Pat least one 6 in four rolls Pno 6's in four rolls.} b) Find the probability of getting at least one double 6 when rolling two fair dice 4 times. {Hint: The probability of rolling a double 6 with a pair of fair dice is 36, and P at least one double 6 in 4 rolls Pno double 6's in 4 rolls.} c) What is the fewest number of rolls so that the probability of getting at least one double 6 is greater than? Tails You Lose. 54. Three fair coins are tossed and, after each toss, those coins that come up tails are removed, and the remaining coins tossed again. What is the probability that in exactly three rounds of tosses, all the coins will have been removed? {Hint: How can this happen? 3 heads, 3 heads, 3 tails 3 heads, heads, tails 3 heads, head, tail heads, heads, tails heads, head, tail head, head, tail }
26 In a certain region of the country, a committee is considering an optimal jury size. A decision by a jury is made on the basis of a simple majority. If there are an even number of people on a jury, the result could be a tie (hung jury) in which case there is a retrial. Retrials are expensive. Moreover, an incorrect decision on the part of a jury is considered unacceptable. Thus optimal jury size to this committee means that size which has the greatest chance of making the correct decision on the first trial when compared to other sizes under consideration. We ll restrict our considerations to juries of size, 3, and 4. Let s suppose there is a probability p, 0 p, of an individual on a jury of making a correct decision. Now assuming that these decisions are made on an independent basis, the probability that a two-person will make a correct decision on the first trial is given by p. In the case of a three-person jury, a correct decision on the first trial results from one of the following: Juror Juror Juror 3 Probability right right right 3 p wrong right right p p right wrong right p p p right right wrong p p So the probability that a three-person jury will make a correct decision on the first trial is given by p 3 3p p. In the case of a four-person jury, a correct decision on the first trial results from one of the following: Juror Juror Juror 3 Juror 4 Probability right right right right 4 p 3 wrong right right right p p right wrong right right p p p right right wrong right p right right right wrong p 3 p So the probability that a four-person jury will make the correct decision on the first trial is given p 4 4p 3 p. The information gained so far is summarized in the following table: by Size of Jury p p Probability of correct decision on first trial p 3 p 3 3p p 4 p 4 4p 3 p Now under the definition of optimal jury size, we would choose a two-person jury over a threeperson jury if 3 p p 3p p Since p 0, we can divide both sides by p to get
27 p 3 p p 3 p p Since this last inequality is never satisfied, it follows that we would never choose a two-person jury over a three-person jury. We would choose a four-person jury over a three-person jury if p 4 p p p 3p p. Again, dividing both sides by Dividing both sides by 3, we get p, we get p 4 p p p 3 p 3p 6 p 3 0 p p 0 p 0 Since this last inequality is impossible, it follows that we would never pick a four-person jury over a three-person jury. The previous analysis indicates that a three-person jury is optimal if one considers two, three, and four-person juries. Let s conclude the discussion by comparing a two-person jury to a four-person jury. We would choose a two-person jury over a four-person jury if 4 3 p p 4p p. Again, dividing both sides by p, we get 4 p p p 3p 4 p 0 p p 3 0 Here s the sign chart for the left side of the last inequality: 0 p 3 We can conclude that we would choose a two-person jury over a four-person jury if a four-person jury over a two-person jury if p. If 3 p, and 3 p, then both have the same chance 3
28 of making the correct decision on the first trial. If p, and in an educated society one would 3 hope that would happen, a four-person jury would be preferable to a two-person jury. Here is a graph of the probability of a correct decision on the first trial by juries of size two, three, and four. Probability of a jury of a given size making a correct decision 3 4 Probability of a single juror making a correct decision, p Trial By Jury. 55. a) Using the definition of optimal jury size, which is preferable, a one-person jury or a three-person jury? b) Using the definition of optimal jury size, which is preferable, a five-person jury or a three-person jury? c) Using the definition of optimal jury size, find the optimal jury size for juries up to size seven.
29 Just The Rope, Not The Cheese. 56. a) A magician cuts a rope into two pieces at a point selected at random. What is the probability that the length of the longer piece of rope is at least 8 times the length of the shorter piece of rope? {Hint: If we call the length of the rope L, then the cut would have to be made in the black portion of the rope indicated in the diagram. L L L 9 9 } b) What is the probability that the length of the longer piece of rope is at least 6 times the length of the shorter piece of rope? Think Of A Letter From A To Z. 57. Each person in a group of people selects a letter of the alphabet at random. What is the fewest number of people that could be in the group if the probability of two or more people choosing the same letter is greater than? {Hint: For the number of people, n, with n 6, the number of ways that everyone chooses a different letter is n or 6 P n. The number of ways that the n people can choose a letter without restriction is 6 n. So the probability that P everyone chooses a different letter is 6 n n. Now use the complement.} 6 Consider the problem of estimating the number of fish in a certain lake. One method is the following: Randomly select a spot on the lake and using a net, get a catch of fish. Suppose that 00 fish are caught. These fish are then tagged and returned to the lake. One week later, another spot is selected and 00 fish are netted with 40 of them having tags. This suggests that 40 or.4 of the total number of fish in the lake are tagged. If F is the total number of fish in 00 the lake, then.4f 00 F F We can generalize the process as follows: Let
30 N N the number of fish caught and tagged the number of fish in the second catch T the number of tagged fish in the second catch F the total number of fish in the lake Then, as before: T F N N F NN T NN T is called a basic estimate for the total number of fish in the lake, F. For example, if N N the number of fish caught and tagged 60 the number of fish in the second catch 80 T the number of tagged fish in the second catch 0 Then a basic estimate for the total number of fish in the lake is given by NN F 480. T 0 Now let s look at this estimation problem from a different point of view. Suppose we play the same game with a small goldfish pond. Suppose that N N the number of fish caught and tagged 3 the number of fish in the second catch 3 T the number of tagged fish in the second catch. NN 33 Our basic estimate for the number of goldfish in the pond is F 9. In general, T the smallest number of fish that could be in the lake or pond is N N T. For this goldfish pond we get Let s calculate the conditional probability of getting tagged fish our of 3 in the second catch, given that the pond actually contains 5 goldfish. P tagged fish out of 3 total of 5 fish
31 # of ways of selecting tagged fish # of ways of selecting untagged fish # of ways of selecting 3 fish C C C We can also calculate the conditional probability of getting tagged fish out of 3 in the second catch, given that the pond actually contains 6 goldfish. P tagged fish out of 3 total of 6 fish # of ways of selecting tagged fish # of ways of selecting untagged fish # of ways of selecting 3 fish C C C It is not unreasonable to say that it is more likely that the pond contains 6 goldfish rather than 5. In general, the formula for the conditional probability of getting tagged fish out of 3 in the second catch, given that the pond actually contains K goldfish is given by P tagged fish out of 3 total of K fish # of ways of selecting tagged fish # of ways of selecting untagged fish # of ways of selecting 3 fish C C 3 K 3. K 3 C Here is a table and graph of conditional probabilities for different values of K: K C C 3 K 3 K 3 C
32 conditional probability Total number of fish From the previous table and graph, it would appear that the most likely number of goldfish in the pond is 8 or 9. Before accepting this, however, there is one question to answer. If the table were continued, is it possible that at some point the probabilities would begin to increase again? In order to answer this question, let s look at which we ll abbreviate as P P tagged fish out of 3 total of K fish tagged fish out of 3 total of K+ fish P K P K. The probabilities in the table will be increasing when and decreasing when C P K P K 3 K 3 3 K and PK P K C K 3 C P K P K, since PK PK C C, so C K 3, since PK PK,. Now we know that 3C K 3C PK K C3 K 3K 4 PK 3C K C K 4k 4. If C K 3
33 we do a polynomial division, we get that this we can conclude that P K P K PK K 8 K PK K and PK P K K K K for 5 8. So from for K 8. From this we have that the conditional probabilities will continue to decrease beyond 9. Therefore we can say that the most likely number of fish in the pond is 8 or 9. We call 8 or 9 a Maximum Likelihood Estimate. Recall that our basic estimate was Suppose that N N Go Jump In The Pond! the number of fish caught and tagged 3 the number of fish in the second catch 4 T the number of tagged fish in the second catch a) What is a basic estimate for the number of fish in the pond? b) What is the fewest number of fish possible in the pond? c) What is the most likely number of fish in the pond? d) Verify that the conditional probabilities will continue to decrease after a certain value. e) How do the basic estimate and the most likely estimate compare?
34 Can You Cut It As An Escort? 59. In 988, the ignition keys for Ford Escorts were made of a blank key with five cuts, each cut made to one of five different depths. a) How many different key types were there? b) If in 988, Ford sold 38,50 Escorts, and assuming that the key types were assigned uniformly to the Escorts, what is the probability that one Escort key will start another one selected at random? {Hint: If the key types were assigned uniformly, then there would be of each type. So for another car s key to match a given car s type, it would have to be one of the remaining keys of that type.} c) If an Escort is selected, what is the probability that a randomly selected key type will start it? The answers in b) and c) aren t close by coincidence. Assuming a uniform assignment of the key types, the probability that a randomly selected Escort key will start another one is N N 3,5 N, where N is the total number of Escorts sold. Notice that 3,5 3,5 N, so for N N large values of N, N 0 N, and 3,5 3,5 N 3,5. N 3,5 N Unrandomly Choose A Random 3-digit Number. 60. Sometimes things which seem random really aren t. For example, a magician writes a number and seals it in an envelope. He asks you to think of a 3-digit number with all the digits the same, but you don t tell him the number. Then he asks you to add the three digits together and divide the original number by this sum. The magician opens the envelope, and shows you the result that you got. What number did the magician seal in the envelope? Show that it will always work. Hint: If the number is aaa, then its value is 00a 0a a a. The sum of the digits is a a a 3a. If you divide the number by the sum of the digits, you get a 3a.
35 Being Unfair With Fair Dice. 6. Sometimes things which seem random really aren t. For example, a magician writes a number and seals it in an envelope. He asks you to roll two standard dice. Then he asks you to multiply the top two numbers, multiply the bottom two numbers, multiply the top of one by the bottom of the other, and multiply the other top and bottom. The magician then asks you to add up the four answers. When the magician opens the envelope, it s the same number. What number did the magician seal in the envelope? Show that it will always work. Hint: Suppose that the numbers are t, b, t, b. On a standard die, opposite numbers add to 7, so t b 7 and t b 7. The sum of the four products is t t b b t b t b. t t bb t b t b t t t b t b bb t t b b t b. Notice that I Won t Just Give You One; I ll Give You Both. 6. Sometimes things which seem random really aren t. For example, have a friend secretly choose a number from to 9 and another number from 0 to 99. Have your friend add the two numbers. Multiply the result by 5. Add the smaller chosen number. Multiply this sum by. Subtract the smaller chosen number. Have your friend give you the result. You should be able to determine the two numbers. Describe how to determine the two numbers. Show that it will always work. Hint: Suppose that the first number is x and the second number is y. Then here s what happens: 5x y x x 5 x y x x x 0y 0 x y x.. Notice that remaining digits to the left one's digit Given a set of numbers a, a, a3,, a n, we would like to find a value, x, which minimizes the sum of its distances from the set of numbers, x a x a x an, and also a value x, which minimizes the sum the squares of its distances from the set of numbers, x a x a x a. n Let s start with minimizing the sum of the squares of the distances: x a x a x an x ax a x ax a x anx an nx a a an x a a an Now let s complete the square on the right side: Factor out the n from the first two terms.
36 n x x a a a n a a a n n Then add the square of half the coefficient of x inside the brackets, and subtract n times this amount on the outside to balance out this addition. nx x a a a n n n a a an a a an a a an n a a an a a a nx a a an n n n The Lesser Known Of The X-men, The Square Minimizer. 63. So what is the special value of x that will minimize the right side of the equation, and what is this minimum value? Let s look at the graph of the sum of the squared distances for some particular sets of numbers: For,,3,4,5, the graph of x x x 3 x 4 x 5 is the following. For,0,3,4,4, the graph of x x x 3 x 4 x 4 is the following.
37 Now let s minimize the sum of the distances, x a x a x an. In this case, we ll look at some specific examples, and we ll look for a pattern. For,,4, the graph of x x x 4 is the following. The piecewise formula is 3x 7; x x 5 ; x x x x 4 x ; x 4 3x7 ; x4
38 For,,6, the graph of x x x 6 is the following. The piecewise formula is 3x 9; x x 7 ; x x x x 6 x 3 ; x 6 3x9 ; x6 For,,5,8,, the graph of x x x 5 x 8 x is the following. The piecewise formula is 5x 6; x 3x 8 ; x x 4 ; x 5 x x x 5 x 8 x x4 ;5 x 8 3x ;8 x 5x6 ; x
39 In these three examples each set contained an odd number of values. Another Lesser Known Of The X-men, The Odd Absolute Minimizer. 64. What is the value of x that minimizes the sum of the distances in the case of an odd number of values? Determine minimizing values of x for the sums of the distances for the following sets: a),,3,4,5,6,7 b),,3, 4,5, 6,7 Let s do an example with an even number of values: For,,4,5, the graph of x x x 4 x 5 is the following. 4x ; x x 0 ; x The piecewise formula is x x x 4 x 5 6 ; x 4 x ;4 x 5 4x ; x5
40 Another Lesser Known Of The X-men, The Even Absolute Minimizer. 65. What s the value of x that minimizes the sum of the distances if there are an even number of values? Determine minimizing values of x for the sums of the distances for the following sets: a),,3,4,5,6 b),,3,3,5,6 The Electric Company On Sesame Street. 66. An electrical station is to be located on a straight street containing six houses. House A is located on one end of the street, House B is located 500 feet from House A, House C is located 600 feet from House A, House D is located 800 feet from House A, House E is located 950 feet from House A, and House F is located 00 feet from House A. How far from House A on the street should the station be located to use the least amount of wire connecting it to each of the 6 houses? Seven matchboxes are arranged in a row, as in the following diagram. The first contains 9 matches, the second 9, and the remaining ones contain 6, 8, 8,, and 4 matches, respectively. Matches may be taken from any matchbox and transferred to any adjacent matchbox. The matches must be redistributed so that the number of matches in each matchbox is the same. How can this be accomplished, shifting as few matches as possible? Matchbox 9 Matchbox 9 Matchbox 3 6 Matchbox 4 8 Matchbox 5 8 Matchbox 6 Matchbox 7 4 There is a total of 05 matches in all the boxes. So in order to have the same number of matches in each of the seven matchboxes, each box must contain 5 matches. The solution of the problem is to shift 4 matches from box to box.
41 Matchbox 5 Matchbox 3 Matchbox 3 6 Matchbox 4 8 Matchbox 5 8 Matchbox 6 Matchbox 7 4 Then shift matches from box 3 to box and 9 matches from box 3 to box 4. Matchbox 5 Matchbox 5 Matchbox 3 5 Matchbox 4 7 Matchbox 5 8 Matchbox 6 Matchbox 7 4 Then shift matches from box 4 to box 5 and 5 matches from box 5 to box 6. Finally, shift match from box 6 to box 7. Matchbox 5 Matchbox 5 Matchbox 3 5 Matchbox 4 5 Matchbox 5 5 Matchbox 6 6 Matchbox 7 4 Matchbox 5 Matchbox 5 Matchbox 3 5 Matchbox 4 5 Matchbox 5 5 Matchbox 6 5 Matchbox 7 5 The total number of shifted matches is
42 An algebraic approach that leads to this result is the following: If matches are shifted from a smaller numbered box to a larger numbered box, then it s considered a positive shift, otherwise, it s considered a negative shift. Shift x matches from box to box. This gives 9 x matches in box and 9 x matches in box. In order to have 5 matches in box, we need to shift x 6 matches from box to box 3. This gives 5 matches in box and x 0 matches in box 3. In order to have 5 matches in box 3, we need to shift x 5 matches from box 3 to box 4. This gives 5 matches in box 3 and x 3 matches in box 4. In order to have 5 matches in box 4, we need to shift x matches from box 4 to box 5. This gives 5 matches in box 4 and x 6 matches in box 5. In order to have 5 matches in box 5, we need to shift x matches from box 5 to box 6. This gives 5 matches in box 5 and x matches in box 6. In order to have 5 matches in box 6, we need to shift x 3 matches from box 6 to box 7. This gives 5 matches in box 6 and x matches in box 7. So the results are the following: Matchbox 9 x Matchbox 5 Matchbox 3 5 Matchbox 4 5 Matchbox 5 5 Matchbox 6 5 Matchbox 7 x x x 6 x 5 x x x 3 The total number of shifted matches is x x 6 x 5 x x x 3, and in order to have 5 matches in each box, we need 9 x 5 and x 5. This leads to x 4 and the number of shifted matches being Matchgame Consider the following arrangement of matchboxes along with the given number of matches in each box: Matchbox Matchbox Matchbox 3 3 Matchbox 4 7 Matchbox 5 3 Matchbox 6 0 Matchbox 7 0 Matches may be taken from any matchbox and transferred to any adjacent matchbox. The matches must be redistributed so that the number of matches in each matchbox is the same. How can this be accomplished, shifting as few matches as possible? Now suppose that the seven matchboxes are arranged in a circle:
43 It is permissible to move matches from any box to any adjacent box. The matches must be shifted in such a way that the number of matches in all the boxes becomes the same. How can this be done, shifting as few matches as possible? An algebraic approach is the following: If matches are shifted from a smaller numbered box to a larger numbered box, then it s considered a positive shift, otherwise, it s considered a negative shift. Shift x matches from box to box. This gives 9 x matches in box and 9 x matches in box. In order to have 5 matches in box, we need to shift x 6 matches from box to box 3. This gives 5 matches in box and x 0 matches in box 3. In order to have 5 matches in box 3, we need to shift x 5 matches from box 3 to box 4. This gives 5 matches in box 3 and x 3 matches in box 4. In order to have 5 matches in box 4, we need to shift x matches from box 4 to box 5. This gives 5 matches in box 4 and x 6 matches in box 5. In order to have 5 matches in box 5, we need to shift x matches from box 5 to box 6. This gives 5 matches in box 5 and x matches in box 6. In order to have 5 matches in box 6, we need to shift x 3 matches from box 6 to box 7. This gives 5 matches in box 6 and x matches in box 7. In order to have 5 matches in box 7, we need to shift x 4 matches from box 7 to box. This gives 5 matches in box 7 and 5 matches in box. So the results are the following: x 3 5 x x 5 x 6 5 x x x 5
Probability Problems for Group 1 (Due by Oct. 26)
 Probability Problems for Group (Due by Oct. 26) Don t Lose Your Marbles!. An urn contains 5 red, 6 blue, and 8 green marbles. If a set of 3 marbles is randomly selected, without replacement, a) what is
Probability Problems for Group (Due by Oct. 26) Don t Lose Your Marbles!. An urn contains 5 red, 6 blue, and 8 green marbles. If a set of 3 marbles is randomly selected, without replacement, a) what is
Probability(Due by Oct. 9)
 Probability(Due by Oct. 9) Don t Lose Your Marbles!. An urn contains 5 red, 6 blue, and 8 green marbles. If a set of marbles is randomly selected, without replacement, a) what is the probability that all
Probability(Due by Oct. 9) Don t Lose Your Marbles!. An urn contains 5 red, 6 blue, and 8 green marbles. If a set of marbles is randomly selected, without replacement, a) what is the probability that all
Counting Problems for Group 2(Due by EOC Sep. 27)
 Counting Problems for Group 2(Due by EOC Sep. 27) Arsenio Says, Show Me The Digits! 1. a) From the digits 0, 1, 2, 3, 4, 5, 6, how many four-digit numbers with distinct digits can be constructed? {0463
Counting Problems for Group 2(Due by EOC Sep. 27) Arsenio Says, Show Me The Digits! 1. a) From the digits 0, 1, 2, 3, 4, 5, 6, how many four-digit numbers with distinct digits can be constructed? {0463
Probability and Counting Techniques
 Probability and Counting Techniques Diana Pell (Multiplication Principle) Suppose that a task consists of t choices performed consecutively. Suppose that choice 1 can be performed in m 1 ways; for each
Probability and Counting Techniques Diana Pell (Multiplication Principle) Suppose that a task consists of t choices performed consecutively. Suppose that choice 1 can be performed in m 1 ways; for each
Counting Problems for Group 1 (Due by EOC Feb. 27)
 Counting Problems for Group 1 (Due by EOC Feb. 27) Not All Things Must Pass. 1. Forty-one students each took three exams: one in Algebra, one in Biology, and one in Chemistry. Here are the results 12 failed
Counting Problems for Group 1 (Due by EOC Feb. 27) Not All Things Must Pass. 1. Forty-one students each took three exams: one in Algebra, one in Biology, and one in Chemistry. Here are the results 12 failed
4.1 Sample Spaces and Events
 4.1 Sample Spaces and Events An experiment is an activity that has observable results. Examples: Tossing a coin, rolling dice, picking marbles out of a jar, etc. The result of an experiment is called an
4.1 Sample Spaces and Events An experiment is an activity that has observable results. Examples: Tossing a coin, rolling dice, picking marbles out of a jar, etc. The result of an experiment is called an
The Teachers Circle Mar. 20, 2012 HOW TO GAMBLE IF YOU MUST (I ll bet you $5 that if you give me $10, I ll give you $20.)
 The Teachers Circle Mar. 2, 22 HOW TO GAMBLE IF YOU MUST (I ll bet you $ that if you give me $, I ll give you $2.) Instructor: Paul Zeitz (zeitzp@usfca.edu) Basic Laws and Definitions of Probability If
The Teachers Circle Mar. 2, 22 HOW TO GAMBLE IF YOU MUST (I ll bet you $ that if you give me $, I ll give you $2.) Instructor: Paul Zeitz (zeitzp@usfca.edu) Basic Laws and Definitions of Probability If
CSC/MTH 231 Discrete Structures II Spring, Homework 5
 CSC/MTH 231 Discrete Structures II Spring, 2010 Homework 5 Name 1. A six sided die D (with sides numbered 1, 2, 3, 4, 5, 6) is thrown once. a. What is the probability that a 3 is thrown? b. What is the
CSC/MTH 231 Discrete Structures II Spring, 2010 Homework 5 Name 1. A six sided die D (with sides numbered 1, 2, 3, 4, 5, 6) is thrown once. a. What is the probability that a 3 is thrown? b. What is the
3 The multiplication rule/miscellaneous counting problems
 Practice for Exam 1 1 Axioms of probability, disjoint and independent events 1 Suppose P (A 0, P (B 05 (a If A and B are independent, what is P (A B? What is P (A B? (b If A and B are disjoint, what is
Practice for Exam 1 1 Axioms of probability, disjoint and independent events 1 Suppose P (A 0, P (B 05 (a If A and B are independent, what is P (A B? What is P (A B? (b If A and B are disjoint, what is
Chapter 3: PROBABILITY
 Chapter 3 Math 3201 1 3.1 Exploring Probability: P(event) = Chapter 3: PROBABILITY number of outcomes favourable to the event total number of outcomes in the sample space An event is any collection of
Chapter 3 Math 3201 1 3.1 Exploring Probability: P(event) = Chapter 3: PROBABILITY number of outcomes favourable to the event total number of outcomes in the sample space An event is any collection of
Compound Probability. Set Theory. Basic Definitions
 Compound Probability Set Theory A probability measure P is a function that maps subsets of the state space Ω to numbers in the interval [0, 1]. In order to study these functions, we need to know some basic
Compound Probability Set Theory A probability measure P is a function that maps subsets of the state space Ω to numbers in the interval [0, 1]. In order to study these functions, we need to know some basic
Chapter 2. Permutations and Combinations
 2. Permutations and Combinations Chapter 2. Permutations and Combinations In this chapter, we define sets and count the objects in them. Example Let S be the set of students in this classroom today. Find
2. Permutations and Combinations Chapter 2. Permutations and Combinations In this chapter, we define sets and count the objects in them. Example Let S be the set of students in this classroom today. Find
PROBABILITY. 1. Introduction. Candidates should able to:
 PROBABILITY Candidates should able to: evaluate probabilities in simple cases by means of enumeration of equiprobable elementary events (e.g for the total score when two fair dice are thrown), or by calculation
PROBABILITY Candidates should able to: evaluate probabilities in simple cases by means of enumeration of equiprobable elementary events (e.g for the total score when two fair dice are thrown), or by calculation
CSE 312: Foundations of Computing II Quiz Section #2: Inclusion-Exclusion, Pigeonhole, Introduction to Probability (solutions)
 CSE 31: Foundations of Computing II Quiz Section #: Inclusion-Exclusion, Pigeonhole, Introduction to Probability (solutions) Review: Main Theorems and Concepts Binomial Theorem: x, y R, n N: (x + y) n
CSE 31: Foundations of Computing II Quiz Section #: Inclusion-Exclusion, Pigeonhole, Introduction to Probability (solutions) Review: Main Theorems and Concepts Binomial Theorem: x, y R, n N: (x + y) n
Individual 5 th Grade
 Individual 5 th Grade Instructions: Problems 1 10 are multiple choice and count towards your team score. Bubble in the letter on your answer sheet. Be sure to erase all mistakes completely. 1. Which one
Individual 5 th Grade Instructions: Problems 1 10 are multiple choice and count towards your team score. Bubble in the letter on your answer sheet. Be sure to erase all mistakes completely. 1. Which one
3 The multiplication rule/miscellaneous counting problems
 Practice for Exam 1 1 Axioms of probability, disjoint and independent events 1. Suppose P (A) = 0.4, P (B) = 0.5. (a) If A and B are independent, what is P (A B)? What is P (A B)? (b) If A and B are disjoint,
Practice for Exam 1 1 Axioms of probability, disjoint and independent events 1. Suppose P (A) = 0.4, P (B) = 0.5. (a) If A and B are independent, what is P (A B)? What is P (A B)? (b) If A and B are disjoint,
MATH 215 DISCRETE MATHEMATICS INSTRUCTOR: P. WENG
 MATH DISCRETE MATHEMATICS INSTRUCTOR: P. WENG Counting and Probability Suggested Problems Basic Counting Skills, Inclusion-Exclusion, and Complement. (a An office building contains 7 floors and has 7 offices
MATH DISCRETE MATHEMATICS INSTRUCTOR: P. WENG Counting and Probability Suggested Problems Basic Counting Skills, Inclusion-Exclusion, and Complement. (a An office building contains 7 floors and has 7 offices
Name: Class: Date: ID: A
 Class: Date: Chapter 0 review. A lunch menu consists of different kinds of sandwiches, different kinds of soup, and 6 different drinks. How many choices are there for ordering a sandwich, a bowl of soup,
Class: Date: Chapter 0 review. A lunch menu consists of different kinds of sandwiches, different kinds of soup, and 6 different drinks. How many choices are there for ordering a sandwich, a bowl of soup,
1. An office building contains 27 floors and has 37 offices on each floor. How many offices are in the building?
 1. An office building contains 27 floors and has 37 offices on each floor. How many offices are in the building? 2. A particular brand of shirt comes in 12 colors, has a male version and a female version,
1. An office building contains 27 floors and has 37 offices on each floor. How many offices are in the building? 2. A particular brand of shirt comes in 12 colors, has a male version and a female version,
A Probability Work Sheet
 A Probability Work Sheet October 19, 2006 Introduction: Rolling a Die Suppose Geoff is given a fair six-sided die, which he rolls. What are the chances he rolls a six? In order to solve this problem, we
A Probability Work Sheet October 19, 2006 Introduction: Rolling a Die Suppose Geoff is given a fair six-sided die, which he rolls. What are the chances he rolls a six? In order to solve this problem, we
CHAPTER 9 - COUNTING PRINCIPLES AND PROBABILITY
 CHAPTER 9 - COUNTING PRINCIPLES AND PROBABILITY Probability is the Probability is used in many real-world fields, such as insurance, medical research, law enforcement, and political science. Objectives:
CHAPTER 9 - COUNTING PRINCIPLES AND PROBABILITY Probability is the Probability is used in many real-world fields, such as insurance, medical research, law enforcement, and political science. Objectives:
Counting Methods and Probability
 CHAPTER Counting Methods and Probability Many good basketball players can make 90% of their free throws. However, the likelihood of a player making several free throws in a row will be less than 90%. You
CHAPTER Counting Methods and Probability Many good basketball players can make 90% of their free throws. However, the likelihood of a player making several free throws in a row will be less than 90%. You
2008 High School Math Contest Draft #3
 2008 High School Math Contest Draft #3 Elon University April, 2008 Note : In general, figures are drawn not to scale! All decimal answers should be rounded to two decimal places. 1. On average, how often
2008 High School Math Contest Draft #3 Elon University April, 2008 Note : In general, figures are drawn not to scale! All decimal answers should be rounded to two decimal places. 1. On average, how often
7.1 Experiments, Sample Spaces, and Events
 7.1 Experiments, Sample Spaces, and Events An experiment is an activity that has observable results. Examples: Tossing a coin, rolling dice, picking marbles out of a jar, etc. The result of an experiment
7.1 Experiments, Sample Spaces, and Events An experiment is an activity that has observable results. Examples: Tossing a coin, rolling dice, picking marbles out of a jar, etc. The result of an experiment
Algebra II- Chapter 12- Test Review
 Sections: Counting Principle Permutations Combinations Probability Name Choose the letter of the term that best matches each statement or phrase. 1. An illustration used to show the total number of A.
Sections: Counting Principle Permutations Combinations Probability Name Choose the letter of the term that best matches each statement or phrase. 1. An illustration used to show the total number of A.
Empirical (or statistical) probability) is based on. The empirical probability of an event E is the frequency of event E.
 Probability and Statistics Chapter 3 Notes Section 3-1 I. Probability Experiments. A. When weather forecasters say There is a 90% chance of rain tomorrow, or a doctor says There is a 35% chance of a successful
Probability and Statistics Chapter 3 Notes Section 3-1 I. Probability Experiments. A. When weather forecasters say There is a 90% chance of rain tomorrow, or a doctor says There is a 35% chance of a successful
The probability set-up
 CHAPTER 2 The probability set-up 2.1. Introduction and basic theory We will have a sample space, denoted S (sometimes Ω) that consists of all possible outcomes. For example, if we roll two dice, the sample
CHAPTER 2 The probability set-up 2.1. Introduction and basic theory We will have a sample space, denoted S (sometimes Ω) that consists of all possible outcomes. For example, if we roll two dice, the sample
Statistics 1040 Summer 2009 Exam III
 Statistics 1040 Summer 2009 Exam III 1. For the following basic probability questions. Give the RULE used in the appropriate blank (BEFORE the question), for each of the following situations, using one
Statistics 1040 Summer 2009 Exam III 1. For the following basic probability questions. Give the RULE used in the appropriate blank (BEFORE the question), for each of the following situations, using one
The probability set-up
 CHAPTER The probability set-up.1. Introduction and basic theory We will have a sample space, denoted S sometimes Ω that consists of all possible outcomes. For example, if we roll two dice, the sample space
CHAPTER The probability set-up.1. Introduction and basic theory We will have a sample space, denoted S sometimes Ω that consists of all possible outcomes. For example, if we roll two dice, the sample space
The study of probability is concerned with the likelihood of events occurring. Many situations can be analyzed using a simplified model of probability
 The study of probability is concerned with the likelihood of events occurring Like combinatorics, the origins of probability theory can be traced back to the study of gambling games Still a popular branch
The study of probability is concerned with the likelihood of events occurring Like combinatorics, the origins of probability theory can be traced back to the study of gambling games Still a popular branch
Chapter 9 Miscellaneous Examples
 Miscellaneous Examples 9. The use of "Complementary Events" at a suitable time may help to solve the problem. Example Assume that a single torpedo ( 魚雷 ) has a probability 6 of sinking a ship, a probability
Miscellaneous Examples 9. The use of "Complementary Events" at a suitable time may help to solve the problem. Example Assume that a single torpedo ( 魚雷 ) has a probability 6 of sinking a ship, a probability
INDIAN STATISTICAL INSTITUTE
 INDIAN STATISTICAL INSTITUTE B1/BVR Probability Home Assignment 1 20-07-07 1. A poker hand means a set of five cards selected at random from usual deck of playing cards. (a) Find the probability that it
INDIAN STATISTICAL INSTITUTE B1/BVR Probability Home Assignment 1 20-07-07 1. A poker hand means a set of five cards selected at random from usual deck of playing cards. (a) Find the probability that it
Dependence. Math Circle. October 15, 2016
 Dependence Math Circle October 15, 2016 1 Warm up games 1. Flip a coin and take it if the side of coin facing the table is a head. Otherwise, you will need to pay one. Will you play the game? Why? 2. If
Dependence Math Circle October 15, 2016 1 Warm up games 1. Flip a coin and take it if the side of coin facing the table is a head. Otherwise, you will need to pay one. Will you play the game? Why? 2. If
Introduction to Mathematical Reasoning, Saylor 111
 Here s a game I like plying with students I ll write a positive integer on the board that comes from a set S You can propose other numbers, and I tell you if your proposed number comes from the set Eventually
Here s a game I like plying with students I ll write a positive integer on the board that comes from a set S You can propose other numbers, and I tell you if your proposed number comes from the set Eventually
Unit 9: Probability Assignments
 Unit 9: Probability Assignments #1: Basic Probability In each of exercises 1 & 2, find the probability that the spinner shown would land on (a) red, (b) yellow, (c) blue. 1. 2. Y B B Y B R Y Y B R 3. Suppose
Unit 9: Probability Assignments #1: Basic Probability In each of exercises 1 & 2, find the probability that the spinner shown would land on (a) red, (b) yellow, (c) blue. 1. 2. Y B B Y B R Y Y B R 3. Suppose
Algebra 2 Notes Section 10.1: Apply the Counting Principle and Permutations
 Algebra 2 Notes Section 10.1: Apply the Counting Principle and Permutations Objective(s): Vocabulary: I. Fundamental Counting Principle: Two Events: Three or more Events: II. Permutation: (top of p. 684)
Algebra 2 Notes Section 10.1: Apply the Counting Principle and Permutations Objective(s): Vocabulary: I. Fundamental Counting Principle: Two Events: Three or more Events: II. Permutation: (top of p. 684)
MAT104: Fundamentals of Mathematics II Summary of Counting Techniques and Probability. Preliminary Concepts, Formulas, and Terminology
 MAT104: Fundamentals of Mathematics II Summary of Counting Techniques and Probability Preliminary Concepts, Formulas, and Terminology Meanings of Basic Arithmetic Operations in Mathematics Addition: Generally
MAT104: Fundamentals of Mathematics II Summary of Counting Techniques and Probability Preliminary Concepts, Formulas, and Terminology Meanings of Basic Arithmetic Operations in Mathematics Addition: Generally
6) A) both; happy B) neither; not happy C) one; happy D) one; not happy
 MATH 00 -- PRACTICE TEST 2 Millersville University, Spring 202 Ron Umble, Instr. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all natural
MATH 00 -- PRACTICE TEST 2 Millersville University, Spring 202 Ron Umble, Instr. MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find all natural
Chapter 1. Probability
 Chapter 1. Probability 1.1 Basic Concepts Scientific method a. For a given problem, we define measures that explains the problem well. b. Data is collected with observation and the measures are calculated.
Chapter 1. Probability 1.1 Basic Concepts Scientific method a. For a given problem, we define measures that explains the problem well. b. Data is collected with observation and the measures are calculated.
Probability. The MEnTe Program Math Enrichment through Technology. Title V East Los Angeles College
 Probability The MEnTe Program Math Enrichment through Technology Title V East Los Angeles College 2003 East Los Angeles College. All rights reserved. Topics Introduction Empirical Probability Theoretical
Probability The MEnTe Program Math Enrichment through Technology Title V East Los Angeles College 2003 East Los Angeles College. All rights reserved. Topics Introduction Empirical Probability Theoretical
Fundamentals of Probability
 Fundamentals of Probability Introduction Probability is the likelihood that an event will occur under a set of given conditions. The probability of an event occurring has a value between 0 and 1. An impossible
Fundamentals of Probability Introduction Probability is the likelihood that an event will occur under a set of given conditions. The probability of an event occurring has a value between 0 and 1. An impossible
COUNTING AND PROBABILITY
 CHAPTER 9 COUNTING AND PROBABILITY It s as easy as 1 2 3. That s the saying. And in certain ways, counting is easy. But other aspects of counting aren t so simple. Have you ever agreed to meet a friend
CHAPTER 9 COUNTING AND PROBABILITY It s as easy as 1 2 3. That s the saying. And in certain ways, counting is easy. But other aspects of counting aren t so simple. Have you ever agreed to meet a friend
Raise your hand if you rode a bus within the past month. Record the number of raised hands.
 166 CHAPTER 3 PROBABILITY TOPICS Raise your hand if you rode a bus within the past month. Record the number of raised hands. Raise your hand if you answered "yes" to BOTH of the first two questions. Record
166 CHAPTER 3 PROBABILITY TOPICS Raise your hand if you rode a bus within the past month. Record the number of raised hands. Raise your hand if you answered "yes" to BOTH of the first two questions. Record
Foundations of Probability Worksheet Pascal
 Foundations of Probability Worksheet Pascal The basis of probability theory can be traced back to a small set of major events that set the stage for the development of the field as a branch of mathematics.
Foundations of Probability Worksheet Pascal The basis of probability theory can be traced back to a small set of major events that set the stage for the development of the field as a branch of mathematics.
6. In how many different ways can you answer 10 multiple-choice questions if each question has five choices?
 Pre-Calculus Section 4.1 Multiplication, Addition, and Complement 1. Evaluate each of the following: a. 5! b. 6! c. 7! d. 0! 2. Evaluate each of the following: a. 10! b. 20! 9! 18! 3. In how many different
Pre-Calculus Section 4.1 Multiplication, Addition, and Complement 1. Evaluate each of the following: a. 5! b. 6! c. 7! d. 0! 2. Evaluate each of the following: a. 10! b. 20! 9! 18! 3. In how many different
Discrete probability and the laws of chance
 Chapter 8 Discrete probability and the laws of chance 8.1 Multiple Events and Combined Probabilities 1 Determine the probability of each of the following events assuming that the die has equal probability
Chapter 8 Discrete probability and the laws of chance 8.1 Multiple Events and Combined Probabilities 1 Determine the probability of each of the following events assuming that the die has equal probability
April 10, ex) Draw a tree diagram of this situation.
 April 10, 2014 12-1 Fundamental Counting Principle & Multiplying Probabilities 1. Outcome - the result of a single trial. 2. Sample Space - the set of all possible outcomes 3. Independent Events - when
April 10, 2014 12-1 Fundamental Counting Principle & Multiplying Probabilities 1. Outcome - the result of a single trial. 2. Sample Space - the set of all possible outcomes 3. Independent Events - when
Name: Class: Date: 6. An event occurs, on average, every 6 out of 17 times during a simulation. The experimental probability of this event is 11
 Class: Date: Sample Mastery # Multiple Choice Identify the choice that best completes the statement or answers the question.. One repetition of an experiment is known as a(n) random variable expected value
Class: Date: Sample Mastery # Multiple Choice Identify the choice that best completes the statement or answers the question.. One repetition of an experiment is known as a(n) random variable expected value
For all questions, answer choice E) NOTA means that none of the above answers is correct.
 For all questions, answer choice means that none of the above answers is correct. 1. How many distinct permutations are there for the letters in the word MUALPHATHETA? 1! 4! B) 1! 3! C) 1!! D) 1!. A fair
For all questions, answer choice means that none of the above answers is correct. 1. How many distinct permutations are there for the letters in the word MUALPHATHETA? 1! 4! B) 1! 3! C) 1!! D) 1!. A fair
Introduction. Firstly however we must look at the Fundamental Principle of Counting (sometimes referred to as the multiplication rule) which states:
 Worksheet 4.11 Counting Section 1 Introduction When looking at situations involving counting it is often not practical to count things individually. Instead techniques have been developed to help us count
Worksheet 4.11 Counting Section 1 Introduction When looking at situations involving counting it is often not practical to count things individually. Instead techniques have been developed to help us count
MAT104: Fundamentals of Mathematics II Counting Techniques Class Exercises Solutions
 MAT104: Fundamentals of Mathematics II Counting Techniques Class Exercises Solutions 1. Appetizers: Salads: Entrées: Desserts: 2. Letters: (A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U,
MAT104: Fundamentals of Mathematics II Counting Techniques Class Exercises Solutions 1. Appetizers: Salads: Entrées: Desserts: 2. Letters: (A, B, C, D, E, F, G, H, I, J, K, L, M, N, O, P, Q, R, S, T, U,
Name: Spring P. Walston/A. Moore. Topic worksheet # assigned #completed Teacher s Signature Tree Diagrams FCP
 Name: Spring 2016 P. Walston/A. Moore Topic worksheet # assigned #completed Teacher s Signature Tree Diagrams 1-0 13 FCP 1-1 16 Combinations/ Permutations Factorials 1-2 22 1-3 20 Intro to Probability
Name: Spring 2016 P. Walston/A. Moore Topic worksheet # assigned #completed Teacher s Signature Tree Diagrams 1-0 13 FCP 1-1 16 Combinations/ Permutations Factorials 1-2 22 1-3 20 Intro to Probability
Here are two situations involving chance:
 Obstacle Courses 1. Introduction. Here are two situations involving chance: (i) Someone rolls a die three times. (People usually roll dice in pairs, so dice is more common than die, the singular form.)
Obstacle Courses 1. Introduction. Here are two situations involving chance: (i) Someone rolls a die three times. (People usually roll dice in pairs, so dice is more common than die, the singular form.)
1. How many subsets are there for the set of cards in a standard playing card deck? How many subsets are there of size 8?
 Math 1711-A Summer 2016 Final Review 1 August 2016 Time Limit: 170 Minutes Name: 1. How many subsets are there for the set of cards in a standard playing card deck? How many subsets are there of size 8?
Math 1711-A Summer 2016 Final Review 1 August 2016 Time Limit: 170 Minutes Name: 1. How many subsets are there for the set of cards in a standard playing card deck? How many subsets are there of size 8?
Chapter 1. Probability
 Chapter 1. Probability 1.1 Basic Concepts Scientific method a. For a given problem, we define measures that explains the problem well. b. Data is collected with observation and the measures are calculated.
Chapter 1. Probability 1.1 Basic Concepts Scientific method a. For a given problem, we define measures that explains the problem well. b. Data is collected with observation and the measures are calculated.
2 Event is equally likely to occur or not occur. When all outcomes are equally likely, the theoretical probability that an event A will occur is:
 10.3 TEKS a.1, a.4 Define and Use Probability Before You determined the number of ways an event could occur. Now You will find the likelihood that an event will occur. Why? So you can find real-life geometric
10.3 TEKS a.1, a.4 Define and Use Probability Before You determined the number of ways an event could occur. Now You will find the likelihood that an event will occur. Why? So you can find real-life geometric
LC OL Probability. ARNMaths.weebly.com. As part of Leaving Certificate Ordinary Level Math you should be able to complete the following.
 A Ryan LC OL Probability ARNMaths.weebly.com Learning Outcomes As part of Leaving Certificate Ordinary Level Math you should be able to complete the following. Counting List outcomes of an experiment Apply
A Ryan LC OL Probability ARNMaths.weebly.com Learning Outcomes As part of Leaving Certificate Ordinary Level Math you should be able to complete the following. Counting List outcomes of an experiment Apply
1. The sides of a cube are increased by 100%. By how many percent 1. percent does the volume of the cube increase?
 Blitz, Page 1 1. The sides of a cube are increased by 100%. By how many percent 1. percent does the volume of the cube increase? 2. How many primes are there between 90 and 100? 2. 3. Approximately how
Blitz, Page 1 1. The sides of a cube are increased by 100%. By how many percent 1. percent does the volume of the cube increase? 2. How many primes are there between 90 and 100? 2. 3. Approximately how
PROBABILITY TOPIC TEST MU ALPHA THETA 2007
 PROBABILITY TOPI TEST MU ALPHA THETA 00. Richard has red marbles and white marbles. Richard s friends, Vann and Penelo, each select marbles from the bag. What is the probability that Vann selects red marble
PROBABILITY TOPI TEST MU ALPHA THETA 00. Richard has red marbles and white marbles. Richard s friends, Vann and Penelo, each select marbles from the bag. What is the probability that Vann selects red marble
Instructions: Choose the best answer and shade in the corresponding letter on the answer sheet provided. Be sure to include your name and student ID.
 Math 3201 Unit 3 Probability Test 1 Unit Test Name: Part 1 Selected Response: Instructions: Choose the best answer and shade in the corresponding letter on the answer sheet provided. Be sure to include
Math 3201 Unit 3 Probability Test 1 Unit Test Name: Part 1 Selected Response: Instructions: Choose the best answer and shade in the corresponding letter on the answer sheet provided. Be sure to include
Chapter 11: Probability and Counting Techniques
 Chapter 11: Probability and Counting Techniques Diana Pell Section 11.3: Basic Concepts of Probability Definition 1. A sample space is a set of all possible outcomes of an experiment. Exercise 1. An experiment
Chapter 11: Probability and Counting Techniques Diana Pell Section 11.3: Basic Concepts of Probability Definition 1. A sample space is a set of all possible outcomes of an experiment. Exercise 1. An experiment
Math is Cool Masters
 Sponsored by: Algebra II January 6, 008 Individual Contest Tear this sheet off and fill out top of answer sheet on following page prior to the start of the test. GENERAL INSTRUCTIONS applying to all tests:
Sponsored by: Algebra II January 6, 008 Individual Contest Tear this sheet off and fill out top of answer sheet on following page prior to the start of the test. GENERAL INSTRUCTIONS applying to all tests:
Due Friday February 17th before noon in the TA drop box, basement, AP&M. HOMEWORK 3 : HAND IN ONLY QUESTIONS: 2, 4, 8, 11, 13, 15, 21, 24, 27
 Exercise Sheet 3 jacques@ucsd.edu Due Friday February 17th before noon in the TA drop box, basement, AP&M. HOMEWORK 3 : HAND IN ONLY QUESTIONS: 2, 4, 8, 11, 13, 15, 21, 24, 27 1. A six-sided die is tossed.
Exercise Sheet 3 jacques@ucsd.edu Due Friday February 17th before noon in the TA drop box, basement, AP&M. HOMEWORK 3 : HAND IN ONLY QUESTIONS: 2, 4, 8, 11, 13, 15, 21, 24, 27 1. A six-sided die is tossed.
2006 Pascal Contest (Grade 9)
 Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2006 Pascal Contest (Grade 9) Wednesday, February 22, 2006
Canadian Mathematics Competition An activity of the Centre for Education in Mathematics and Computing, University of Waterloo, Waterloo, Ontario 2006 Pascal Contest (Grade 9) Wednesday, February 22, 2006
Introduction to Counting and Probability
 Randolph High School Math League 2013-2014 Page 1 If chance will have me king, why, chance may crown me. Shakespeare, Macbeth, Act I, Scene 3 1 Introduction Introduction to Counting and Probability Counting
Randolph High School Math League 2013-2014 Page 1 If chance will have me king, why, chance may crown me. Shakespeare, Macbeth, Act I, Scene 3 1 Introduction Introduction to Counting and Probability Counting
commands Homework D1 Q.1.
 > commands > > Homework D1 Q.1. If you enter the lottery by choosing 4 different numbers from a set of 47 numbers, how many ways are there to choose your numbers? Answer: Use the C(n,r) formula. C(47,4)
> commands > > Homework D1 Q.1. If you enter the lottery by choosing 4 different numbers from a set of 47 numbers, how many ways are there to choose your numbers? Answer: Use the C(n,r) formula. C(47,4)
Section : Combinations and Permutations
 Section 11.1-11.2: Combinations and Permutations Diana Pell A construction crew has three members. A team of two must be chosen for a particular job. In how many ways can the team be chosen? How many words
Section 11.1-11.2: Combinations and Permutations Diana Pell A construction crew has three members. A team of two must be chosen for a particular job. In how many ways can the team be chosen? How many words
Math 1313 Section 6.2 Definition of Probability
 Math 1313 Section 6.2 Definition of Probability Probability is a measure of the likelihood that an event occurs. For example, if there is a 20% chance of rain tomorrow, that means that the probability
Math 1313 Section 6.2 Definition of Probability Probability is a measure of the likelihood that an event occurs. For example, if there is a 20% chance of rain tomorrow, that means that the probability
CPM Educational Program
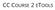 CC COURSE 2 ETOOLS Table of Contents General etools... 5 Algebra Tiles (CPM)... 6 Pattern Tile & Dot Tool (CPM)... 9 Area and Perimeter (CPM)...11 Base Ten Blocks (CPM)...14 +/- Tiles & Number Lines (CPM)...16
CC COURSE 2 ETOOLS Table of Contents General etools... 5 Algebra Tiles (CPM)... 6 Pattern Tile & Dot Tool (CPM)... 9 Area and Perimeter (CPM)...11 Base Ten Blocks (CPM)...14 +/- Tiles & Number Lines (CPM)...16
Name Date Trial 1: Capture distances with only decimeter markings. Name Trial 1 Trial 2 Trial 3 Average
 Decimal Drop Name Date Trial 1: Capture distances with only decimeter markings. Name Trial 1 Trial 2 Trial 3 Average Trial 2: Capture distances with centimeter markings Name Trial 1 Trial 2 Trial 3 Average
Decimal Drop Name Date Trial 1: Capture distances with only decimeter markings. Name Trial 1 Trial 2 Trial 3 Average Trial 2: Capture distances with centimeter markings Name Trial 1 Trial 2 Trial 3 Average
18.S34 (FALL, 2007) PROBLEMS ON PROBABILITY
 18.S34 (FALL, 2007) PROBLEMS ON PROBABILITY 1. Three closed boxes lie on a table. One box (you don t know which) contains a $1000 bill. The others are empty. After paying an entry fee, you play the following
18.S34 (FALL, 2007) PROBLEMS ON PROBABILITY 1. Three closed boxes lie on a table. One box (you don t know which) contains a $1000 bill. The others are empty. After paying an entry fee, you play the following
CHAPTER 7 Probability
 CHAPTER 7 Probability 7.1. Sets A set is a well-defined collection of distinct objects. Welldefined means that we can determine whether an object is an element of a set or not. Distinct means that we can
CHAPTER 7 Probability 7.1. Sets A set is a well-defined collection of distinct objects. Welldefined means that we can determine whether an object is an element of a set or not. Distinct means that we can
Mat 344F challenge set #2 Solutions
 Mat 344F challenge set #2 Solutions. Put two balls into box, one ball into box 2 and three balls into box 3. The remaining 4 balls can now be distributed in any way among the three remaining boxes. This
Mat 344F challenge set #2 Solutions. Put two balls into box, one ball into box 2 and three balls into box 3. The remaining 4 balls can now be distributed in any way among the three remaining boxes. This
Chapter 1 - Set Theory
 Midterm review Math 3201 Name: Chapter 1 - Set Theory Part 1: Multiple Choice : 1) U = {hockey, basketball, golf, tennis, volleyball, soccer}. If B = {sports that use a ball}, which element would be in
Midterm review Math 3201 Name: Chapter 1 - Set Theory Part 1: Multiple Choice : 1) U = {hockey, basketball, golf, tennis, volleyball, soccer}. If B = {sports that use a ball}, which element would be in
Find the probability of an event by using the definition of probability
 LESSON 10-1 Probability Lesson Objectives Find the probability of an event by using the definition of probability Vocabulary experiment (p. 522) trial (p. 522) outcome (p. 522) sample space (p. 522) event
LESSON 10-1 Probability Lesson Objectives Find the probability of an event by using the definition of probability Vocabulary experiment (p. 522) trial (p. 522) outcome (p. 522) sample space (p. 522) event
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Mathematical Ideas Chapter 2 Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) In one town, 2% of all voters are Democrats. If two voters
Mathematical Ideas Chapter 2 Review Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. ) In one town, 2% of all voters are Democrats. If two voters
Probability Paradoxes
 Probability Paradoxes Washington University Math Circle February 20, 2011 1 Introduction We re all familiar with the idea of probability, even if we haven t studied it. That is what makes probability so
Probability Paradoxes Washington University Math Circle February 20, 2011 1 Introduction We re all familiar with the idea of probability, even if we haven t studied it. That is what makes probability so
Intermediate Math Circles November 1, 2017 Probability I
 Intermediate Math Circles November 1, 2017 Probability I Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application.
Intermediate Math Circles November 1, 2017 Probability I Probability is the study of uncertain events or outcomes. Games of chance that involve rolling dice or dealing cards are one obvious area of application.
Math 227 Elementary Statistics. Bluman 5 th edition
 Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 4 Probability and Counting Rules 2 Objectives Determine sample spaces and find the probability of an event using classical probability or empirical
Math 227 Elementary Statistics Bluman 5 th edition CHAPTER 4 Probability and Counting Rules 2 Objectives Determine sample spaces and find the probability of an event using classical probability or empirical
CS 237: Probability in Computing
 CS 237: Probability in Computing Wayne Snyder Computer Science Department Boston University Lecture 5: o Independence reviewed; Bayes' Rule o Counting principles and combinatorics; o Counting considered
CS 237: Probability in Computing Wayne Snyder Computer Science Department Boston University Lecture 5: o Independence reviewed; Bayes' Rule o Counting principles and combinatorics; o Counting considered
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Study Guide for Test III (MATH 1630) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the number of subsets of the set. 1) {x x is an even
Study Guide for Test III (MATH 1630) Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. Find the number of subsets of the set. 1) {x x is an even
Discrete Structures for Computer Science
 Discrete Structures for Computer Science William Garrison bill@cs.pitt.edu 6311 Sennott Square Lecture #23: Discrete Probability Based on materials developed by Dr. Adam Lee The study of probability is
Discrete Structures for Computer Science William Garrison bill@cs.pitt.edu 6311 Sennott Square Lecture #23: Discrete Probability Based on materials developed by Dr. Adam Lee The study of probability is
Page 1 of 22. Website: Mobile:
 Exercise 15.1 Question 1: Complete the following statements: (i) Probability of an event E + Probability of the event not E =. (ii) The probability of an event that cannot happen is. Such as event is called.
Exercise 15.1 Question 1: Complete the following statements: (i) Probability of an event E + Probability of the event not E =. (ii) The probability of an event that cannot happen is. Such as event is called.
a) 2, 4, 8, 14, 22, b) 1, 5, 6, 10, 11, c) 3, 9, 21, 39, 63, d) 3, 0, 6, 15, 27, e) 3, 8, 13, 18, 23,
 Pre-alculus Midterm Exam Review Name:. Which of the following is an arithmetic sequence?,, 8,,, b),, 6, 0,, c), 9,, 9, 6, d), 0, 6,, 7, e), 8,, 8,,. What is a rule for the nth term of the arithmetic sequence
Pre-alculus Midterm Exam Review Name:. Which of the following is an arithmetic sequence?,, 8,,, b),, 6, 0,, c), 9,, 9, 6, d), 0, 6,, 7, e), 8,, 8,,. What is a rule for the nth term of the arithmetic sequence
Section The Multiplication Principle and Permutations
 Section 2.1 - The Multiplication Principle and Permutations Example 1: A yogurt shop has 4 flavors (chocolate, vanilla, strawberry, and blueberry) and three sizes (small, medium, and large). How many different
Section 2.1 - The Multiplication Principle and Permutations Example 1: A yogurt shop has 4 flavors (chocolate, vanilla, strawberry, and blueberry) and three sizes (small, medium, and large). How many different
Combinatorics: The Fine Art of Counting
 Combinatorics: The Fine Art of Counting The Final Challenge Part One You have 30 minutes to solve as many of these problems as you can. You will likely not have time to answer all the questions, so pick
Combinatorics: The Fine Art of Counting The Final Challenge Part One You have 30 minutes to solve as many of these problems as you can. You will likely not have time to answer all the questions, so pick
Class XII Chapter 13 Probability Maths. Exercise 13.1
 Exercise 13.1 Question 1: Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E F) = 0.2, find P (E F) and P(F E). It is given that P(E) = 0.6, P(F) = 0.3, and P(E F) = 0.2 Question 2:
Exercise 13.1 Question 1: Given that E and F are events such that P(E) = 0.6, P(F) = 0.3 and P(E F) = 0.2, find P (E F) and P(F E). It is given that P(E) = 0.6, P(F) = 0.3, and P(E F) = 0.2 Question 2:
4.2.4 What if both events happen?
 4.2.4 What if both events happen? Unions, Intersections, and Complements In the mid 1600 s, a French nobleman, the Chevalier de Mere, was wondering why he was losing money on a bet that he thought was
4.2.4 What if both events happen? Unions, Intersections, and Complements In the mid 1600 s, a French nobleman, the Chevalier de Mere, was wondering why he was losing money on a bet that he thought was
Eighth Grade Test - Excellence in Mathematics Contest
 1. The sum of two natural numbers is 100 and their positive difference is 42. What is the positive difference of the squares of these two natural numbers?. 1600. 200. 600. 4200. 400 2. The sum of 16 consecutive
1. The sum of two natural numbers is 100 and their positive difference is 42. What is the positive difference of the squares of these two natural numbers?. 1600. 200. 600. 4200. 400 2. The sum of 16 consecutive
EECS 203 Spring 2016 Lecture 15 Page 1 of 6
 EECS 203 Spring 2016 Lecture 15 Page 1 of 6 Counting We ve been working on counting for the last two lectures. We re going to continue on counting and probability for about 1.5 more lectures (including
EECS 203 Spring 2016 Lecture 15 Page 1 of 6 Counting We ve been working on counting for the last two lectures. We re going to continue on counting and probability for about 1.5 more lectures (including
Solutions for the Practice Final
 Solutions for the Practice Final 1. Ian and Nai play the game of todo, where at each stage one of them flips a coin and then rolls a die. The person who played gets as many points as the number rolled
Solutions for the Practice Final 1. Ian and Nai play the game of todo, where at each stage one of them flips a coin and then rolls a die. The person who played gets as many points as the number rolled
3 PROBABILITY TOPICS
 Chapter 3 Probability Topics 35 3 PROBABILITY TOPICS Figure 3. Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Chapter 3 Probability Topics 35 3 PROBABILITY TOPICS Figure 3. Meteor showers are rare, but the probability of them occurring can be calculated. (credit: Navicore/flickr) Introduction It is often necessary
Independence Is The Word
 Problem 1 Simulating Independent Events Describe two different events that are independent. Describe two different events that are not independent. The probability of obtaining a tail with a coin toss
Problem 1 Simulating Independent Events Describe two different events that are independent. Describe two different events that are not independent. The probability of obtaining a tail with a coin toss
Probability: introduction
 May 6, 2009 Probability: introduction page 1 Probability: introduction Probability is the part of mathematics that deals with the chance or the likelihood that things will happen The probability of an
May 6, 2009 Probability: introduction page 1 Probability: introduction Probability is the part of mathematics that deals with the chance or the likelihood that things will happen The probability of an
6. a) Determine the probability distribution. b) Determine the expected sum of two dice. c) Repeat parts a) and b) for the sum of
 d) generating a random number between 1 and 20 with a calculator e) guessing a person s age f) cutting a card from a well-shuffled deck g) rolling a number with two dice 3. Given the following probability
d) generating a random number between 1 and 20 with a calculator e) guessing a person s age f) cutting a card from a well-shuffled deck g) rolling a number with two dice 3. Given the following probability
Date. Probability. Chapter
 Date Probability Contests, lotteries, and games offer the chance to win just about anything. You can win a cup of coffee. Even better, you can win cars, houses, vacations, or millions of dollars. Games
Date Probability Contests, lotteries, and games offer the chance to win just about anything. You can win a cup of coffee. Even better, you can win cars, houses, vacations, or millions of dollars. Games
Meet #5 March Intermediate Mathematics League of Eastern Massachusetts
 Meet #5 March 2008 Intermediate Mathematics League of Eastern Massachusetts Meet #5 March 2008 Category 1 Mystery 1. In the diagram to the right, each nonoverlapping section of the large rectangle is
Meet #5 March 2008 Intermediate Mathematics League of Eastern Massachusetts Meet #5 March 2008 Category 1 Mystery 1. In the diagram to the right, each nonoverlapping section of the large rectangle is
1. How to identify the sample space of a probability experiment and how to identify simple events
 Statistics Chapter 3 Name: 3.1 Basic Concepts of Probability Learning objectives: 1. How to identify the sample space of a probability experiment and how to identify simple events 2. How to use the Fundamental
Statistics Chapter 3 Name: 3.1 Basic Concepts of Probability Learning objectives: 1. How to identify the sample space of a probability experiment and how to identify simple events 2. How to use the Fundamental
Chapter 5 - Elementary Probability Theory
 Chapter 5 - Elementary Probability Theory Historical Background Much of the early work in probability concerned games and gambling. One of the first to apply probability to matters other than gambling
Chapter 5 - Elementary Probability Theory Historical Background Much of the early work in probability concerned games and gambling. One of the first to apply probability to matters other than gambling
Independent and Mutually Exclusive Events
 Independent and Mutually Exclusive Events By: OpenStaxCollege Independent and mutually exclusive do not mean the same thing. Independent Events Two events are independent if the following are true: P(A
Independent and Mutually Exclusive Events By: OpenStaxCollege Independent and mutually exclusive do not mean the same thing. Independent Events Two events are independent if the following are true: P(A
