Automata and Formal Languages - CM0081 Turing Machines
|
|
|
- Edith Jocelin Griffin
- 6 years ago
- Views:
Transcription
1 Automata and Formal Languages - CM0081 Turing Machines Andrés Sicard-Ramírez Universidad EAFIT Semester
2 Turing Machines Alan Mathison Turing ( ) Automata and Formal Languages - CM0081. Turing Machines 2/45
3 Turing Machines (TM) Unbounded tape divided into discrete squares which contain symbols from a finite alphabet Automata and Formal Languages - CM0081. Turing Machines 3/45
4 Turing Machines (TM) Unbounded tape divided into discrete squares which contain symbols from a finite alphabet Read/Write head Automata and Formal Languages - CM0081. Turing Machines 4/45
5 Turing Machines (TM) Unbounded tape divided into discrete squares which contain symbols from a finite alphabet Read/Write head Finite set of instructions (transition function) Automata and Formal Languages - CM0081. Turing Machines 5/45
6 Turing Machines (TM) Unbounded tape divided into discrete squares which contain symbols from a finite alphabet Read/Write head Finite set of instructions (transition function) Move of a TM (tape symbol under the head, current state): change state, rewrite the symbol and move the head one square Automata and Formal Languages - CM0081. Turing Machines 6/45
7 Turing Machines A Turing machine is a 7-tuple M = (Q, Σ, Γ, δ, q 0, B, F ) where Q: A finite set of states Σ: An alphabet of input symbols Γ: An alphabet of tape symbols (Σ Γ) δ Q Γ Q Γ D: A transition (partial) function where D = {L, R} is the set of moves q 0 Q: A start state B: The blank symbol (B Γ, B Σ) F Q: A set of final or accepting states Automata and Formal Languages - CM0081. Turing Machines 7/45
8 Transition Diagrams for Turing Machines Example start Y /Y 0/0 Y /Y 0/0 q 0 0/X 1/Y q 1 q 2 Y /Y X/X Y /Y B/B q 3 q 4 where Σ = {0, 1} and Γ = {0, 1, X, Y, B}. Automata and Formal Languages - CM0081. Turing Machines 8/45
9 Transition Tables for Turing Machines Example The machine of the previous example is given by M = ({q 0, q 1, q 2.q 3, q 4 }, {0, 1}, {0, 1, X, Y, B}, δ, q 0, B, {q 4 }) where δ is given by state 0 1 X Y B q 0 (q 1, X, R) (q 3, Y, R) q 1 (q 1, 0, R) (q 2, Y, L) (q 1, Y, R) q 2 (q 2, 0, L) (q 0, X, R) (q 2, Y, L) q 3 (q 3, Y, R) (q 4, B, R) q 4 Automata and Formal Languages - CM0081. Turing Machines 9/45
10 Quintuples for Turing Machines Example The machine of the previous example is given by M = ({q 0, q 1, q 2.q 3, q 4 }, {0, 1}, {0, 1, X, Y, B}, δ, q 0, B, {q 4 }), where δ is given by q 0, 0, X, R, q 1 q 0, Y, Y, R, q 3 q 1, 0, 0, R, q 1 q 1, 1, Y, L, q 2 q 1, Y, Y, R, q 1 q 2, 0, 0, L, q 2 q 2, X, X, R, q 0 q 2, Y, Y, L, q 2 q 3, Y, Y, R, q 3 q 3, B, B, R, q 4 Automata and Formal Languages - CM0081. Turing Machines 10/45
11 Instantaneous Descriptions for Turing Machines Definition An instantaneous description of a TM is a string where i) q is the state of the TM, X 1 X 2 X i 1 qx i X i+1 X n ii) the head is scanning the i-th symbol from the left and iii) X 1 X 2 X n is the portion of the tape between the leftmost and rightmost non-blank. Automata and Formal Languages - CM0081. Turing Machines 11/45
12 Instantaneous Descriptions for Turing Machines Notation : Move of the TM M from an instantaneous descriptions to another. M M : Zero o more moves of the TM M. Automata and Formal Languages - CM0081. Turing Machines 12/45
13 Instantaneous Descriptions for Turing Machines Example q 0 X 0 1 q M Xq 1 01 M X0q 2 1 q 1 q M X0q 2 1 X 0 1 q 2 Automata and Formal Languages - CM0081. Turing Machines 13/45
14 Recursively Enumerable Languages Definition Let M = (Q, Σ, Γ, δ, q 0, B, F ) be a TM. The language accepted by M is L(M) = {w Σ q 0 w M αpβ}, where p F and α, β Γ. Automata and Formal Languages - CM0081. Turing Machines 14/45
15 Recursively Enumerable Languages Definition Let M = (Q, Σ, Γ, δ, q 0, B, F ) be a TM. The language accepted by M is L(M) = {w Σ q 0 w M αpβ}, where p F and α, β Γ. Definition A language L is recursively enumerable (RE) if exists a TM M such L = L(M). Automata and Formal Languages - CM0081. Turing Machines 15/45
16 Recursively Enumerable Languages Example Let M be the machine described by the previous diagram. Then L(M) = {0 n 1 n n 1}. See the simulation in the course website. Automata and Formal Languages - CM0081. Turing Machines 16/45
17 Recursive Languages Convention We assume that a TM halts if it accepts. Automata and Formal Languages - CM0081. Turing Machines 17/45
18 Recursive Languages Convention We assume that a TM halts if it accepts. What about if the TM does not accept? Automata and Formal Languages - CM0081. Turing Machines 18/45
19 Recursive Languages Convention We assume that a TM halts if it accepts. What about if the TM does not accept? Recall Recall that a language L is recursively enumerable if exists a TM M such that L = L(M). Automata and Formal Languages - CM0081. Turing Machines 19/45
20 Recursive Languages Convention We assume that a TM halts if it accepts. What about if the TM does not accept? Recall Recall that a language L is recursively enumerable if exists a TM M such that L = L(M). Definition A language L is recursive if exists a TM M such that i) L = L(M) and ii) M always halt (even if it does not accept) Automata and Formal Languages - CM0081. Turing Machines 20/45
21 Turing Machine Computable Functions Number-theoretical functions {f f N k N} Automata and Formal Languages - CM0081. Turing Machines 21/45
22 Turing Machine Computable Functions Number-theoretical functions {f f N k N} Codification n = 0 n = 0 0 n times (n 1, n 2,, n k ) = n 1 1 n n k for n N for (n 1, n 2,, n k ) N k Automata and Formal Languages - CM0081. Turing Machines 22/45
23 Turing Machine Computable Functions Definition A function f N N is Turing machine computable iff exists a machine M = (Q, {0, 1}, Γ, δ, q 0, B) (there are not accepting states) such that for all n N: From the initial instantaneous description q 0 n the machine halts with f(n) on its tape, surrounded by blanks. Automata and Formal Languages - CM0081. Turing Machines 23/45
24 Turing Machine Computable Functions Definition A function f N N is Turing machine computable iff exists a machine M = (Q, {0, 1}, Γ, δ, q 0, B) (there are not accepting states) such that for all n N: From the initial instantaneous description q 0 n the machine halts with f(n) on its tape, surrounded by blanks. Remark: The definition extends to functions f N k N. Automata and Formal Languages - CM0081. Turing Machines 24/45
25 Turing Machine Computable Functions Example The proper subtraction function is Turing machine computable. m n, m n = { Initial instantaneous description: q 0 0 m 10 n Final information on the tape: 0 m n if m n; 0, otherwise. See the simulation in the course homepage. Automata and Formal Languages - CM0081. Turing Machines 25/45
26 Turing Machine Computable Functions Examples The following functions are Turing machine computable: z(x) = 0 s(x) = x + 1 Ik n(x 1,, x n ) = x k i(x) = x f k (x) = k x + y, xy, x y (zero function) (successor function) (n-ary projection functions) (identity function) (k-constant function) (addition, multiplication and exponentiation) Automata and Formal Languages - CM0081. Turing Machines 26/45
27 Equivalence between Function Computation and Language Recognition Example (Hopcroft, Motwani and Ullman [2007], Exercise 8.2.4) Define the graph of a function f N N to be the set of all strings of the form [ x, f(x)]. Automata and Formal Languages - CM0081. Turing Machines 27/45
28 Equivalence between Function Computation and Language Recognition Example (Hopcroft, Motwani and Ullman [2007], Exercise 8.2.4) Define the graph of a function f N N to be the set of all strings of the form [ x, f(x)]. A Turing machine is said to compute the function f N N if, started with x on its tape, it halts (in any state) with f(x) on its tape. Automata and Formal Languages - CM0081. Turing Machines 28/45
29 Equivalence between Function Computation and Language Recognition Example (Hopcroft, Motwani and Ullman [2007], Exercise 8.2.4) Define the graph of a function f N N to be the set of all strings of the form [ x, f(x)]. A Turing machine is said to compute the function f N N if, started with x on its tape, it halts (in any state) with f(x) on its tape. Answer the following, with informal, but clear constructions. Automata and Formal Languages - CM0081. Turing Machines 29/45
30 Equivalence between Function Computation and Language Recognition Example (cont.) 1. Show how, given a TM that computes f, you can construct a TM that accepts the graph of f as a language. Automata and Formal Languages - CM0081. Turing Machines 30/45
31 Equivalence between Function Computation and Language Recognition Example (cont.) 1. Show how, given a TM that computes f, you can construct a TM that accepts the graph of f as a language. 2. Show how, given a TM that accepts the graph of f, you can construct a TM that computes f. Automata and Formal Languages - CM0081. Turing Machines 31/45
32 Equivalence between Function Computation and Language Recognition Example (cont.) 1. Show how, given a TM that computes f, you can construct a TM that accepts the graph of f as a language. 2. Show how, given a TM that accepts the graph of f, you can construct a TM that computes f. 3. A function is said to partial if it may be undefined for some arguments. If we extend the ideas of this exercise to partial functions, then we do not require that the TM computing f halts if its input x is one of the natural numbers for which f(x) is not defined. Automata and Formal Languages - CM0081. Turing Machines 32/45
33 Equivalence between Function Computation and Language Recognition Example (cont.) 1. Show how, given a TM that computes f, you can construct a TM that accepts the graph of f as a language. 2. Show how, given a TM that accepts the graph of f, you can construct a TM that computes f. 3. A function is said to partial if it may be undefined for some arguments. If we extend the ideas of this exercise to partial functions, then we do not require that the TM computing f halts if its input x is one of the natural numbers for which f(x) is not defined. Do your constructions for parts (1) and (2) work if the function f is partial? If not, explain how you could modify the constructions to make it work. Automata and Formal Languages - CM0081. Turing Machines 33/45
34 Restrictions to Turing Machines Automata and Formal Languages - CM0081. Turing Machines 34/45
35 Restrictions to Turing Machines Restrictions Turing machines with semi-unbounded tapes Automata and Formal Languages - CM0081. Turing Machines 35/45
36 Restrictions to Turing Machines Restrictions Turing machines with semi-unbounded tapes Multi-stack machines Automata and Formal Languages - CM0081. Turing Machines 36/45
37 Restrictions to Turing Machines Restrictions Turing machines with semi-unbounded tapes Multi-stack machines Theorem The previous restrictions are equivalents to Turing machines. Automata and Formal Languages - CM0081. Turing Machines 37/45
38 Extensions to Turing Machines Automata and Formal Languages - CM0081. Turing Machines 38/45
39 Extensions to Turing Machines Extensions Multi-tape Turing machines Automata and Formal Languages - CM0081. Turing Machines 39/45
40 Extensions to Turing Machines Extensions Multi-tape Turing machines Mutil-dimensional tape Turing machines Automata and Formal Languages - CM0081. Turing Machines 40/45
41 Extensions to Turing Machines Extensions Multi-tape Turing machines Mutil-dimensional tape Turing machines Multi-head Turing machines Automata and Formal Languages - CM0081. Turing Machines 41/45
42 Extensions to Turing Machines Extensions Multi-tape Turing machines Mutil-dimensional tape Turing machines Multi-head Turing machines Non-deterministic Turing machines Automata and Formal Languages - CM0081. Turing Machines 42/45
43 Extensions to Turing Machines Extensions Multi-tape Turing machines Mutil-dimensional tape Turing machines Multi-head Turing machines Non-deterministic Turing machines Subroutines Automata and Formal Languages - CM0081. Turing Machines 43/45
44 Extensions to Turing Machines Extensions Multi-tape Turing machines Mutil-dimensional tape Turing machines Multi-head Turing machines Non-deterministic Turing machines Subroutines Theorem The previous extensions are equivalents to Turing machines. Automata and Formal Languages - CM0081. Turing Machines 44/45
45 References Hopcroft, J. E., Motwani, R. and Ullman, J. D. (2007). Introduction to Automata theory, Languages, and Computation. 3rd ed. Pearson Education. Automata and Formal Languages - CM0081. Turing Machines 45/45
Computability. What can be computed?
 Computability What can be computed? Computability What can be computed? read/write tape 0 1 1 0 control Computability What can be computed? read/write tape 0 1 1 0 control Computability What can be computed?
Computability What can be computed? Computability What can be computed? read/write tape 0 1 1 0 control Computability What can be computed? read/write tape 0 1 1 0 control Computability What can be computed?
CITS2211 Discrete Structures Turing Machines
 CITS2211 Discrete Structures Turing Machines October 23, 2017 Highlights We have seen that FSMs and PDAs are surprisingly powerful But there are some languages they can not recognise We will study a new
CITS2211 Discrete Structures Turing Machines October 23, 2017 Highlights We have seen that FSMs and PDAs are surprisingly powerful But there are some languages they can not recognise We will study a new
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI
 DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6503 THEORY OF COMPUTATION 2 Mark Questions & Answers Year / Semester: III / V Regulation: 2013 Academic year:
DHANALAKSHMI COLLEGE OF ENGINEERING, CHENNAI Department of Computer Science and Engineering CS6503 THEORY OF COMPUTATION 2 Mark Questions & Answers Year / Semester: III / V Regulation: 2013 Academic year:
Technical framework of Operating System using Turing Machines
 Reviewed Paper Technical framework of Operating System using Turing Machines Paper ID IJIFR/ V2/ E2/ 028 Page No 465-470 Subject Area Computer Science Key Words Turing, Undesirability, Complexity, Snapshot
Reviewed Paper Technical framework of Operating System using Turing Machines Paper ID IJIFR/ V2/ E2/ 028 Page No 465-470 Subject Area Computer Science Key Words Turing, Undesirability, Complexity, Snapshot
of the hypothesis, but it would not lead to a proof. P 1
 Church-Turing thesis The intuitive notion of an effective procedure or algorithm has been mentioned several times. Today the Turing machine has become the accepted formalization of an algorithm. Clearly
Church-Turing thesis The intuitive notion of an effective procedure or algorithm has been mentioned several times. Today the Turing machine has become the accepted formalization of an algorithm. Clearly
Implementation of Recursively Enumerable Languages in Universal Turing Machine
 Implementation of Recursively Enumerable Languages in Universal Turing Machine Sumitha C.H, Member, ICMLC and Krupa Ophelia Geddam Abstract This paper presents the design and working of a Universal Turing
Implementation of Recursively Enumerable Languages in Universal Turing Machine Sumitha C.H, Member, ICMLC and Krupa Ophelia Geddam Abstract This paper presents the design and working of a Universal Turing
Turing Machines (TM)
 1 Introduction Turing Machines (TM) Jay Bagga A Turing Machine (TM) is a powerful model which represents a general purpose computer. The Church-Turing thesis states that our intuitive notion of algorithms
1 Introduction Turing Machines (TM) Jay Bagga A Turing Machine (TM) is a powerful model which represents a general purpose computer. The Church-Turing thesis states that our intuitive notion of algorithms
CSCI3390-Lecture 8: Undecidability of a special case of the tiling problem
 CSCI3390-Lecture 8: Undecidability of a special case of the tiling problem February 16, 2016 Here we show that the constrained tiling problem from the last lecture (tiling the first quadrant with a designated
CSCI3390-Lecture 8: Undecidability of a special case of the tiling problem February 16, 2016 Here we show that the constrained tiling problem from the last lecture (tiling the first quadrant with a designated
Introduction To Automata Theory Languages And Computation Addison Wesley Series In Computer Science
 Introduction To Automata Theory Languages And Computation Addison Wesley Series In Computer Science INTRODUCTION TO AUTOMATA THEORY LANGUAGES AND COMPUTATION ADDISON WESLEY SERIES IN COMPUTER SCIENCE PDF
Introduction To Automata Theory Languages And Computation Addison Wesley Series In Computer Science INTRODUCTION TO AUTOMATA THEORY LANGUAGES AND COMPUTATION ADDISON WESLEY SERIES IN COMPUTER SCIENCE PDF
Multiplayer Pushdown Games. Anil Seth IIT Kanpur
 Multiplayer Pushdown Games Anil Seth IIT Kanpur Multiplayer Games we Consider These games are played on graphs (finite or infinite) Generalize two player infinite games. Any number of players are allowed.
Multiplayer Pushdown Games Anil Seth IIT Kanpur Multiplayer Games we Consider These games are played on graphs (finite or infinite) Generalize two player infinite games. Any number of players are allowed.
Tiling Problems. This document supersedes the earlier notes posted about the tiling problem. 1 An Undecidable Problem about Tilings of the Plane
 Tiling Problems This document supersedes the earlier notes posted about the tiling problem. 1 An Undecidable Problem about Tilings of the Plane The undecidable problems we saw at the start of our unit
Tiling Problems This document supersedes the earlier notes posted about the tiling problem. 1 An Undecidable Problem about Tilings of the Plane The undecidable problems we saw at the start of our unit
Computing Permutations with Stacks and Deques
 Michael Albert 1 Mike Atkinson 1 Steve Linton 2 1 Department of Computer Science, University of Otago 2 School of Computer Science, University of St Andrews 7th Australia New Zealand Mathematics Convention
Michael Albert 1 Mike Atkinson 1 Steve Linton 2 1 Department of Computer Science, University of Otago 2 School of Computer Science, University of St Andrews 7th Australia New Zealand Mathematics Convention
Pin-Permutations and Structure in Permutation Classes
 and Structure in Permutation Classes Frédérique Bassino Dominique Rossin Journées de Combinatoire de Bordeaux, feb. 2009 liafa Main result of the talk Conjecture[Brignall, Ruškuc, Vatter]: The pin-permutation
and Structure in Permutation Classes Frédérique Bassino Dominique Rossin Journées de Combinatoire de Bordeaux, feb. 2009 liafa Main result of the talk Conjecture[Brignall, Ruškuc, Vatter]: The pin-permutation
SRM UNIVERSITY FACULTY OF ENGINEERING AND TECHNOLOGY
 SRM UNIVERSITY FACULTY OF ENGINEERING AND TECHNOLOGY SCHOOL OF COMPUTER SCIENCE AND ENGINEERING DEPARTMENT OF CSE COURSE PLAN Course Code : CS0204 Course Title : Theory of Computation Semester : IV Course
SRM UNIVERSITY FACULTY OF ENGINEERING AND TECHNOLOGY SCHOOL OF COMPUTER SCIENCE AND ENGINEERING DEPARTMENT OF CSE COURSE PLAN Course Code : CS0204 Course Title : Theory of Computation Semester : IV Course
THE ENUMERATION OF PERMUTATIONS SORTABLE BY POP STACKS IN PARALLEL
 THE ENUMERATION OF PERMUTATIONS SORTABLE BY POP STACKS IN PARALLEL REBECCA SMITH Department of Mathematics SUNY Brockport Brockport, NY 14420 VINCENT VATTER Department of Mathematics Dartmouth College
THE ENUMERATION OF PERMUTATIONS SORTABLE BY POP STACKS IN PARALLEL REBECCA SMITH Department of Mathematics SUNY Brockport Brockport, NY 14420 VINCENT VATTER Department of Mathematics Dartmouth College
CDT314 FABER Formal Languages, Automata and Models of Computation MARK BURGIN INDUCTIVE TURING MACHINES
 CDT314 FABER Formal Languages, Automata and Models of Computation MARK BURGIN INDUCTIVE TURING MACHINES 2012 1 Inductive Turing Machines Burgin, M. Inductive Turing Machines, Notices of the Academy of
CDT314 FABER Formal Languages, Automata and Models of Computation MARK BURGIN INDUCTIVE TURING MACHINES 2012 1 Inductive Turing Machines Burgin, M. Inductive Turing Machines, Notices of the Academy of
Membrane Computing as Multi Turing Machines
 Volume 4 No.8, December 2012 www.ijais.org Membrane Computing as Multi Turing Machines Mahmoud Abdelaziz Amr Badr Ibrahim Farag ABSTRACT A Turing machine (TM) can be adapted to simulate the logic of any
Volume 4 No.8, December 2012 www.ijais.org Membrane Computing as Multi Turing Machines Mahmoud Abdelaziz Amr Badr Ibrahim Farag ABSTRACT A Turing machine (TM) can be adapted to simulate the logic of any
Honors Algebra 2 Assignment Sheet - Chapter 1
 Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
Assignment Sheet - Chapter 1 #01: Read the text and the examples in your book for the following sections: 1.1, 1., and 1.4. Be sure you read and understand the handshake problem. Also make sure you copy
CSCI 1590 Intro to Computational Complexity
 CSCI 1590 Intro to Computational Complexity Parallel Computation and Complexity Classes John Savage Brown University April 13, 2009 John Savage (Brown University) CSCI 1590 Intro to Computational Complexity
CSCI 1590 Intro to Computational Complexity Parallel Computation and Complexity Classes John Savage Brown University April 13, 2009 John Savage (Brown University) CSCI 1590 Intro to Computational Complexity
Outline. In One Slide. LR Parsing. LR Parsing. No Stopping The Parsing! Bottom-Up Parsing. LR(1) Parsing Tables #2
 LR Parsing Bottom-Up Parsing #1 Outline No Stopping The Parsing! Bottom-Up Parsing LR Parsing Shift and Reduce LR(1) Parsing Algorithm LR(1) Parsing Tables #2 In One Slide An LR(1) parser reads tokens
LR Parsing Bottom-Up Parsing #1 Outline No Stopping The Parsing! Bottom-Up Parsing LR Parsing Shift and Reduce LR(1) Parsing Algorithm LR(1) Parsing Tables #2 In One Slide An LR(1) parser reads tokens
Some algorithmic and combinatorial problems on permutation classes
 Some algorithmic and combinatorial problems on permutation classes The point of view of decomposition trees PhD Defense, 2009 December the 4th Outline 1 Objects studied : Permutations, Patterns and Classes
Some algorithmic and combinatorial problems on permutation classes The point of view of decomposition trees PhD Defense, 2009 December the 4th Outline 1 Objects studied : Permutations, Patterns and Classes
Computer Science 1001.py. Lecture 25 : Intro to Error Correction and Detection Codes
 Computer Science 1001.py Lecture 25 : Intro to Error Correction and Detection Codes Instructors: Daniel Deutch, Amiram Yehudai Teaching Assistants: Michal Kleinbort, Amir Rubinstein School of Computer
Computer Science 1001.py Lecture 25 : Intro to Error Correction and Detection Codes Instructors: Daniel Deutch, Amiram Yehudai Teaching Assistants: Michal Kleinbort, Amir Rubinstein School of Computer
PUZZLES ON GRAPHS: THE TOWERS OF HANOI, THE SPIN-OUT PUZZLE, AND THE COMBINATION PUZZLE
 PUZZLES ON GRAPHS: THE TOWERS OF HANOI, THE SPIN-OUT PUZZLE, AND THE COMBINATION PUZZLE LINDSAY BAUN AND SONIA CHAUHAN ADVISOR: PAUL CULL OREGON STATE UNIVERSITY ABSTRACT. The Towers of Hanoi is a well
PUZZLES ON GRAPHS: THE TOWERS OF HANOI, THE SPIN-OUT PUZZLE, AND THE COMBINATION PUZZLE LINDSAY BAUN AND SONIA CHAUHAN ADVISOR: PAUL CULL OREGON STATE UNIVERSITY ABSTRACT. The Towers of Hanoi is a well
The Tiling Problem. Nikhil Gopalkrishnan. December 08, 2008
 The Tiling Problem Nikhil Gopalkrishnan December 08, 2008 1 Introduction A Wang tile [12] is a unit square with each edge colored from a finite set of colors Σ. A set S of Wang tiles is said to tile a
The Tiling Problem Nikhil Gopalkrishnan December 08, 2008 1 Introduction A Wang tile [12] is a unit square with each edge colored from a finite set of colors Σ. A set S of Wang tiles is said to tile a
Independence of Path and Conservative Vector Fields
 Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
RE-DESIGNING THE PACMAN GAME USING PUSH DOWN AUTOMATA
 Page50 RE-DESIGNING THE PACMAN GAME USING PUSH DOWN AUTOMATA Ariana Yunita a, Riestiya Zain Fadillah b, Muhammad Redho Darmawan c, Andika Dwi Gutomo Putra d, a,b Universitas Pertamina, Jakarta, Indonesia
Page50 RE-DESIGNING THE PACMAN GAME USING PUSH DOWN AUTOMATA Ariana Yunita a, Riestiya Zain Fadillah b, Muhammad Redho Darmawan c, Andika Dwi Gutomo Putra d, a,b Universitas Pertamina, Jakarta, Indonesia
DVA325 Formal Languages, Automata and Models of Computation (FABER)
 DVA325 Formal Languages, Automata and Models of Computation (FABER) Lecture 1 - Introduction School of Innovation, Design and Engineering Mälardalen University 11 November 2014 Abu Naser Masud FABER November
DVA325 Formal Languages, Automata and Models of Computation (FABER) Lecture 1 - Introduction School of Innovation, Design and Engineering Mälardalen University 11 November 2014 Abu Naser Masud FABER November
Modeling Supervisory Control of Autonomous Mobile Robots using Graph Theory, Automata and Z Notation
 Modeling Supervisory Control of Autonomous Mobile Robots using Graph Theory, Automata and Z Notation Javed Iqbal 1, Sher Afzal Khan 2, Nazir Ahmad Zafar 3 and Farooq Ahmad 1 1 Faculty of Information Technology,
Modeling Supervisory Control of Autonomous Mobile Robots using Graph Theory, Automata and Z Notation Javed Iqbal 1, Sher Afzal Khan 2, Nazir Ahmad Zafar 3 and Farooq Ahmad 1 1 Faculty of Information Technology,
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
Basic Science for Software Developers
 Basic Science for Software Developers David Lorge Parnas, P.Eng. Michael Soltys Department of Computing and Software Faculty of Engineering McMaster University, Hamilton, Ontario, Canada - L8S 4K1 1 Introduction
Basic Science for Software Developers David Lorge Parnas, P.Eng. Michael Soltys Department of Computing and Software Faculty of Engineering McMaster University, Hamilton, Ontario, Canada - L8S 4K1 1 Introduction
14.4. Tangent Planes. Tangent Planes. Tangent Planes. Tangent Planes. Partial Derivatives. Tangent Planes and Linear Approximations
 14 Partial Derivatives 14.4 and Linear Approximations Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Suppose a surface S has equation z = f(x, y), where
14 Partial Derivatives 14.4 and Linear Approximations Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Suppose a surface S has equation z = f(x, y), where
COSE312: Compilers. Lecture 5 Lexical Analysis (4)
 COSE312: Compilers Lecture 5 Lexical Analysis (4) Hakjoo Oh 2017 Spring Hakjoo Oh COSE312 2017 Spring, Lecture 5 March 20, 2017 1 / 20 Part 3: Automation Transform the lexical specification into an executable
COSE312: Compilers Lecture 5 Lexical Analysis (4) Hakjoo Oh 2017 Spring Hakjoo Oh COSE312 2017 Spring, Lecture 5 March 20, 2017 1 / 20 Part 3: Automation Transform the lexical specification into an executable
Oracle Turing Machine. Kaixiang Wang
 Oracle Turing Machine Kaixiang Wang Pre-background: What is Turing machine Oracle Turing Machine Definition Function Complexity Why Oracle Turing Machine is important Application of Oracle Turing Machine
Oracle Turing Machine Kaixiang Wang Pre-background: What is Turing machine Oracle Turing Machine Definition Function Complexity Why Oracle Turing Machine is important Application of Oracle Turing Machine
Sensors, Signals and Noise
 Sensors, Signals and Noise COURSE OUTLINE Introduction Signals and Noise Filtering Noise Sensors and associated electronics Sergio Cova SENSORS SIGNALS AND NOISE SSN04b FILTERING NOISE rv 2017/01/25 1
Sensors, Signals and Noise COURSE OUTLINE Introduction Signals and Noise Filtering Noise Sensors and associated electronics Sergio Cova SENSORS SIGNALS AND NOISE SSN04b FILTERING NOISE rv 2017/01/25 1
Tile Complexity of Assembly of Length N Arrays and N x N Squares. by John Reif and Harish Chandran
 Tile Complexity of Assembly of Length N Arrays and N x N Squares by John Reif and Harish Chandran Wang Tilings Hao Wang, 1961: Proving theorems by Pattern Recognition II Class of formal systems Modeled
Tile Complexity of Assembly of Length N Arrays and N x N Squares by John Reif and Harish Chandran Wang Tilings Hao Wang, 1961: Proving theorems by Pattern Recognition II Class of formal systems Modeled
Section 15.3 Partial Derivatives
 Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Experiments #6. Convolution and Linear Time Invariant Systems
 Experiments #6 Convolution and Linear Time Invariant Systems 1) Introduction: In this lab we will explain how to use computer programs to perform a convolution operation on continuous time systems and
Experiments #6 Convolution and Linear Time Invariant Systems 1) Introduction: In this lab we will explain how to use computer programs to perform a convolution operation on continuous time systems and
Logical Agents (AIMA - Chapter 7)
 Logical Agents (AIMA - Chapter 7) CIS 391 - Intro to AI 1 Outline 1. Wumpus world 2. Logic-based agents 3. Propositional logic Syntax, semantics, inference, validity, equivalence and satifiability Next
Logical Agents (AIMA - Chapter 7) CIS 391 - Intro to AI 1 Outline 1. Wumpus world 2. Logic-based agents 3. Propositional logic Syntax, semantics, inference, validity, equivalence and satifiability Next
11/18/2015. Outline. Logical Agents. The Wumpus World. 1. Automating Hunt the Wumpus : A different kind of problem
 Outline Logical Agents (AIMA - Chapter 7) 1. Wumpus world 2. Logic-based agents 3. Propositional logic Syntax, semantics, inference, validity, equivalence and satifiability Next Time: Automated Propositional
Outline Logical Agents (AIMA - Chapter 7) 1. Wumpus world 2. Logic-based agents 3. Propositional logic Syntax, semantics, inference, validity, equivalence and satifiability Next Time: Automated Propositional
Math 233. Extrema of Functions of Two Variables Basics
 Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
CSCI 2570 Introduction to Nanocomputing
 CSCI 2570 Introduction to Nanocomputing DNA Tiling John E Savage Computing with DNA Prepare oligonucleotides ( program them ) Prepare solution with multiple strings. Only complementary substrings q and
CSCI 2570 Introduction to Nanocomputing DNA Tiling John E Savage Computing with DNA Prepare oligonucleotides ( program them ) Prepare solution with multiple strings. Only complementary substrings q and
MAT 115: Finite Math for Computer Science Problem Set 5
 MAT 115: Finite Math for Computer Science Problem Set 5 Out: 04/10/2017 Due: 04/17/2017 Instructions: I leave plenty of space on each page for your computation. If you need more sheet, please attach your
MAT 115: Finite Math for Computer Science Problem Set 5 Out: 04/10/2017 Due: 04/17/2017 Instructions: I leave plenty of space on each page for your computation. If you need more sheet, please attach your
International Journal of Combinatorial Optimization Problems and Informatics. E-ISSN:
 International Journal of Combinatorial Optimization Problems and Informatics E-ISSN: 2007-1558 editor@ijcopi.org International Journal of Combinatorial Optimization Problems and Informatics México Karim,
International Journal of Combinatorial Optimization Problems and Informatics E-ISSN: 2007-1558 editor@ijcopi.org International Journal of Combinatorial Optimization Problems and Informatics México Karim,
Automaten und Formale Sprachen alias Theoretische Informatik. Sommersemester 2014
 Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2014 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Who are we? Teacher: Dr.
Automaten und Formale Sprachen alias Theoretische Informatik Sommersemester 2014 Dr. Sander Bruggink Übungsleitung: Jan Stückrath Sander Bruggink Automaten und Formale Sprachen 1 Who are we? Teacher: Dr.
Automatic Enumeration and Random Generation for pattern-avoiding Permutation Classes
 Automatic Enumeration and Random Generation for pattern-avoiding Permutation Classes Adeline Pierrot Institute of Discrete Mathematics and Geometry, TU Wien (Vienna) Permutation Patterns 2014 Joint work
Automatic Enumeration and Random Generation for pattern-avoiding Permutation Classes Adeline Pierrot Institute of Discrete Mathematics and Geometry, TU Wien (Vienna) Permutation Patterns 2014 Joint work
Enhanced Turing Machines
 Enhanced Turing Machines Lecture 28 Sections 10.1-10.2 Robb T. Koether Hampden-Sydney College Wed, Nov 2, 2016 Robb T. Koether (Hampden-Sydney College) Enhanced Turing Machines Wed, Nov 2, 2016 1 / 21
Enhanced Turing Machines Lecture 28 Sections 10.1-10.2 Robb T. Koether Hampden-Sydney College Wed, Nov 2, 2016 Robb T. Koether (Hampden-Sydney College) Enhanced Turing Machines Wed, Nov 2, 2016 1 / 21
132-avoiding Two-stack Sortable Permutations, Fibonacci Numbers, and Pell Numbers
 132-avoiding Two-stack Sortable Permutations, Fibonacci Numbers, and Pell Numbers arxiv:math/0205206v1 [math.co] 19 May 2002 Eric S. Egge Department of Mathematics Gettysburg College Gettysburg, PA 17325
132-avoiding Two-stack Sortable Permutations, Fibonacci Numbers, and Pell Numbers arxiv:math/0205206v1 [math.co] 19 May 2002 Eric S. Egge Department of Mathematics Gettysburg College Gettysburg, PA 17325
Prolog - 3. Prolog Nomenclature
 Append on lists Prolog - 3 Generate and test paradigm n Queens example Unification Informal definition: isomorphism Formal definition: substitution Prolog-3, CS314 Fall 01 BGRyder 1 Prolog Nomenclature
Append on lists Prolog - 3 Generate and test paradigm n Queens example Unification Informal definition: isomorphism Formal definition: substitution Prolog-3, CS314 Fall 01 BGRyder 1 Prolog Nomenclature
Examples: Find the domain and range of the function f(x, y) = 1 x y 2.
 Multivariate Functions In this chapter, we will return to scalar functions; thus the functions that we consider will output points in space as opposed to vectors. However, in contrast to the majority of
Multivariate Functions In this chapter, we will return to scalar functions; thus the functions that we consider will output points in space as opposed to vectors. However, in contrast to the majority of
Logic and the Sizes of Sets
 1/25 Logic and the Sizes of Sets Larry Moss, Indiana University EASLLI 2014 2/25 Map of Some Natural Logics FOL FO 2 + trans Church-Turing first-order logic FO 2 + R is trans RC (tr,opp) Peano-Frege Aristotle
1/25 Logic and the Sizes of Sets Larry Moss, Indiana University EASLLI 2014 2/25 Map of Some Natural Logics FOL FO 2 + trans Church-Turing first-order logic FO 2 + R is trans RC (tr,opp) Peano-Frege Aristotle
FORMAL DEFINITION OF ARTIFICIAL INTELLIGENCE 1
 International Journal "Information Theories & Applications" Vol.12 277 Further works includes services implementation in GRID environment, which will connect computational cluster and other computational
International Journal "Information Theories & Applications" Vol.12 277 Further works includes services implementation in GRID environment, which will connect computational cluster and other computational
Dynamic Games: Backward Induction and Subgame Perfection
 Dynamic Games: Backward Induction and Subgame Perfection Carlos Hurtado Department of Economics University of Illinois at Urbana-Champaign hrtdmrt2@illinois.edu Jun 22th, 2017 C. Hurtado (UIUC - Economics)
Dynamic Games: Backward Induction and Subgame Perfection Carlos Hurtado Department of Economics University of Illinois at Urbana-Champaign hrtdmrt2@illinois.edu Jun 22th, 2017 C. Hurtado (UIUC - Economics)
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
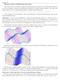 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
You could identify a point on the graph of a function as (x,y) or (x, f(x)). You may have only one function value for each x number.
 Function Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second
Function Before we review exponential and logarithmic functions, let's review the definition of a function and the graph of a function. A function is just a rule. The rule links one number to a second
Permutations of a Multiset Avoiding Permutations of Length 3
 Europ. J. Combinatorics (2001 22, 1021 1031 doi:10.1006/eujc.2001.0538 Available online at http://www.idealibrary.com on Permutations of a Multiset Avoiding Permutations of Length 3 M. H. ALBERT, R. E.
Europ. J. Combinatorics (2001 22, 1021 1031 doi:10.1006/eujc.2001.0538 Available online at http://www.idealibrary.com on Permutations of a Multiset Avoiding Permutations of Length 3 M. H. ALBERT, R. E.
Simple permutations: decidability and unavoidable substructures
 Simple permutations: decidability and unavoidable substructures Robert Brignall a Nik Ruškuc a Vincent Vatter a,,1 a University of St Andrews, School of Mathematics and Statistics, St Andrews, Fife, KY16
Simple permutations: decidability and unavoidable substructures Robert Brignall a Nik Ruškuc a Vincent Vatter a,,1 a University of St Andrews, School of Mathematics and Statistics, St Andrews, Fife, KY16
Formal Verification. Lecture 5: Computation Tree Logic (CTL)
 Formal Verification Lecture 5: Computation Tree Logic (CTL) Jacques Fleuriot 1 jdf@inf.ac.uk 1 With thanks to Bob Atkey for some of the diagrams. Recap Previously: Linear-time Temporal Logic This time:
Formal Verification Lecture 5: Computation Tree Logic (CTL) Jacques Fleuriot 1 jdf@inf.ac.uk 1 With thanks to Bob Atkey for some of the diagrams. Recap Previously: Linear-time Temporal Logic This time:
Reading 14 : Counting
 CS/Math 240: Introduction to Discrete Mathematics Fall 2015 Instructors: Beck Hasti, Gautam Prakriya Reading 14 : Counting In this reading we discuss counting. Often, we are interested in the cardinality
CS/Math 240: Introduction to Discrete Mathematics Fall 2015 Instructors: Beck Hasti, Gautam Prakriya Reading 14 : Counting In this reading we discuss counting. Often, we are interested in the cardinality
code V(n,k) := words module
 Basic Theory Distance Suppose that you knew that an English word was transmitted and you had received the word SHIP. If you suspected that some errors had occurred in transmission, it would be impossible
Basic Theory Distance Suppose that you knew that an English word was transmitted and you had received the word SHIP. If you suspected that some errors had occurred in transmission, it would be impossible
An Aperiodic Tiling from a Dynamical System: An Exposition of An Example of Culik and Kari. S. Eigen J. Navarro V. Prasad
 An Aperiodic Tiling from a Dynamical System: An Exposition of An Example of Culik and Kari S. Eigen J. Navarro V. Prasad These tiles can tile the plane But only Aperiodically Example A (Culik-Kari) Dynamical
An Aperiodic Tiling from a Dynamical System: An Exposition of An Example of Culik and Kari S. Eigen J. Navarro V. Prasad These tiles can tile the plane But only Aperiodically Example A (Culik-Kari) Dynamical
Advanced Automata Theory 4 Games
 Advanced Automata Theory 4 Games Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Advanced Automata Theory 4 Games p. 1 Repetition
Advanced Automata Theory 4 Games Frank Stephan Department of Computer Science Department of Mathematics National University of Singapore fstephan@comp.nus.edu.sg Advanced Automata Theory 4 Games p. 1 Repetition
THE GAME CREATION OPERATOR
 2/6/17 THE GAME CREATION OPERATOR Joint work with Urban Larsson and Matthieu Dufour Silvia Heubach California State University Los Angeles SoCal-Nevada Fall 2016 Section Meeting October 22, 2016 Much of
2/6/17 THE GAME CREATION OPERATOR Joint work with Urban Larsson and Matthieu Dufour Silvia Heubach California State University Los Angeles SoCal-Nevada Fall 2016 Section Meeting October 22, 2016 Much of
Sequential program, state machine, Concurrent process models
 INSIGHT Sequential program, state machine, Concurrent process models Finite State Machines, or automata, originated in computational theory and mathematical models in support of various fields of bioscience.
INSIGHT Sequential program, state machine, Concurrent process models Finite State Machines, or automata, originated in computational theory and mathematical models in support of various fields of bioscience.
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables
 Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Connected Permutations, Hypermaps and Weighted Dyck Words. Robert Cori Mini course, Maps Hypermaps february 2008
 1 Connected Permutations, Hypermaps and Weighted Dyck Words 2 Why? Graph embeddings Nice bijection by Patrice Ossona de Mendez and Pierre Rosenstiehl. Deduce enumerative results. Extensions? 3 Cycles (or
1 Connected Permutations, Hypermaps and Weighted Dyck Words 2 Why? Graph embeddings Nice bijection by Patrice Ossona de Mendez and Pierre Rosenstiehl. Deduce enumerative results. Extensions? 3 Cycles (or
2359 (i.e. 11:59:00 pm) on 4/16/18 via Blackboard
 CS 109: Introduction to Computer Science Goodney Spring 2018 Homework Assignment 4 Assigned: 4/2/18 via Blackboard Due: 2359 (i.e. 11:59:00 pm) on 4/16/18 via Blackboard Notes: a. This is the fourth homework
CS 109: Introduction to Computer Science Goodney Spring 2018 Homework Assignment 4 Assigned: 4/2/18 via Blackboard Due: 2359 (i.e. 11:59:00 pm) on 4/16/18 via Blackboard Notes: a. This is the fourth homework
Reflector A Dynamic Manifestation of Turing Machines with Time and Space Complexity Analysis
 Reflector A Dynamic Manifestation of Turing Machines with Time and Space Complexity Analysis Behroz Mirza MS Computing, Shaheed Zulfikar Ali Bhutto Institute of Science and Technology 90 and 100 Clifton
Reflector A Dynamic Manifestation of Turing Machines with Time and Space Complexity Analysis Behroz Mirza MS Computing, Shaheed Zulfikar Ali Bhutto Institute of Science and Technology 90 and 100 Clifton
Constructing Simple Nonograms of Varying Difficulty
 Constructing Simple Nonograms of Varying Difficulty K. Joost Batenburg,, Sjoerd Henstra, Walter A. Kosters, and Willem Jan Palenstijn Vision Lab, Department of Physics, University of Antwerp, Belgium Leiden
Constructing Simple Nonograms of Varying Difficulty K. Joost Batenburg,, Sjoerd Henstra, Walter A. Kosters, and Willem Jan Palenstijn Vision Lab, Department of Physics, University of Antwerp, Belgium Leiden
Modular Arithmetic. claserken. July 2016
 Modular Arithmetic claserken July 2016 Contents 1 Introduction 2 2 Modular Arithmetic 2 2.1 Modular Arithmetic Terminology.................. 2 2.2 Properties of Modular Arithmetic.................. 2 2.3
Modular Arithmetic claserken July 2016 Contents 1 Introduction 2 2 Modular Arithmetic 2 2.1 Modular Arithmetic Terminology.................. 2 2.2 Properties of Modular Arithmetic.................. 2 2.3
14.2 Limits and Continuity
 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
Classes of permutations avoiding 231 or 321
 Classes of permutations avoiding 231 or 321 Nik Ruškuc nik.ruskuc@st-andrews.ac.uk School of Mathematics and Statistics, University of St Andrews Dresden, 25 November 2015 Aim Introduce the area of pattern
Classes of permutations avoiding 231 or 321 Nik Ruškuc nik.ruskuc@st-andrews.ac.uk School of Mathematics and Statistics, University of St Andrews Dresden, 25 November 2015 Aim Introduce the area of pattern
Lesson 11: Linear and Exponential Investigations
 Hart Interactive Algebra Lesson Lesson : Linear and Exponential Investigations Opening Exercise In this lesson, you ll be exploring linear and exponential function in five different investigations. You
Hart Interactive Algebra Lesson Lesson : Linear and Exponential Investigations Opening Exercise In this lesson, you ll be exploring linear and exponential function in five different investigations. You
RESTRICTED PERMUTATIONS AND POLYGONS. Ghassan Firro and Toufik Mansour Department of Mathematics, University of Haifa, Haifa, Israel
 RESTRICTED PERMUTATIONS AND POLYGONS Ghassan Firro and Toufik Mansour Department of Mathematics, University of Haifa, 905 Haifa, Israel {gferro,toufik}@mathhaifaacil abstract Several authors have examined
RESTRICTED PERMUTATIONS AND POLYGONS Ghassan Firro and Toufik Mansour Department of Mathematics, University of Haifa, 905 Haifa, Israel {gferro,toufik}@mathhaifaacil abstract Several authors have examined
One-Dimensional Peg Solitaire, and Duotaire
 More Games of No Chance MSRI Publications Volume 42, 2002 One-Dimensional Peg Solitaire, and Duotaire CRISTOPHER MOORE AND DAVID EPPSTEIN Abstract. We solve the problem of one-dimensional Peg Solitaire.
More Games of No Chance MSRI Publications Volume 42, 2002 One-Dimensional Peg Solitaire, and Duotaire CRISTOPHER MOORE AND DAVID EPPSTEIN Abstract. We solve the problem of one-dimensional Peg Solitaire.
Outline. Unlimited Register Machine. Intuitive Definition. What is Effective Procedure. Basic Concepts Computable Function
 Outline UnlimitedRegisterMachine Xiaofeng Gao Department of Computer Science and Engineering Shanghai Jiao Tong University, P.R.China CS363-Computability Theory 1 2 3 4 SpecialthanksisgiventoProf.YuxiFuforsharinghisteachingmaterials.
Outline UnlimitedRegisterMachine Xiaofeng Gao Department of Computer Science and Engineering Shanghai Jiao Tong University, P.R.China CS363-Computability Theory 1 2 3 4 SpecialthanksisgiventoProf.YuxiFuforsharinghisteachingmaterials.
Simple Search Algorithms
 Lecture 3 of Artificial Intelligence Simple Search Algorithms AI Lec03/1 Topics of this lecture Random search Search with closed list Search with open list Depth-first and breadth-first search again Uniform-cost
Lecture 3 of Artificial Intelligence Simple Search Algorithms AI Lec03/1 Topics of this lecture Random search Search with closed list Search with open list Depth-first and breadth-first search again Uniform-cost
Chapter 3 PRINCIPLE OF INCLUSION AND EXCLUSION
 Chapter 3 PRINCIPLE OF INCLUSION AND EXCLUSION 3.1 The basics Consider a set of N obects and r properties that each obect may or may not have each one of them. Let the properties be a 1,a,..., a r. Let
Chapter 3 PRINCIPLE OF INCLUSION AND EXCLUSION 3.1 The basics Consider a set of N obects and r properties that each obect may or may not have each one of them. Let the properties be a 1,a,..., a r. Let
Ma/CS 6a Class 16: Permutations
 Ma/CS 6a Class 6: Permutations By Adam Sheffer The 5 Puzzle Problem. Start with the configuration on the left and move the tiles to obtain the configuration on the right. The 5 Puzzle (cont.) The game
Ma/CS 6a Class 6: Permutations By Adam Sheffer The 5 Puzzle Problem. Start with the configuration on the left and move the tiles to obtain the configuration on the right. The 5 Puzzle (cont.) The game
Computability of Tilings
 Computability of Tilings Grégory Lafitte and Michael Weiss Abstract Wang tiles are unit size squares with colored edges. To know whether a given finite set of Wang tiles can tile the plane while respecting
Computability of Tilings Grégory Lafitte and Michael Weiss Abstract Wang tiles are unit size squares with colored edges. To know whether a given finite set of Wang tiles can tile the plane while respecting
Avoiding consecutive patterns in permutations
 Avoiding consecutive patterns in permutations R. E. L. Aldred M. D. Atkinson D. J. McCaughan January 3, 2009 Abstract The number of permutations that do not contain, as a factor (subword), a given set
Avoiding consecutive patterns in permutations R. E. L. Aldred M. D. Atkinson D. J. McCaughan January 3, 2009 Abstract The number of permutations that do not contain, as a factor (subword), a given set
arxiv: v1 [cs.et] 15 Mar 2014
![arxiv: v1 [cs.et] 15 Mar 2014 arxiv: v1 [cs.et] 15 Mar 2014](/thumbs/87/96673767.jpg) Doubles and Negatives are Positive (in Self-Assembly) Jacob Hendricks, Matthew J. Patitz, and Trent A. Rogers arxiv:1403.3841v1 [cs.et] 15 Mar 2014 Abstract. In the abstract Tile Assembly Model (atam),
Doubles and Negatives are Positive (in Self-Assembly) Jacob Hendricks, Matthew J. Patitz, and Trent A. Rogers arxiv:1403.3841v1 [cs.et] 15 Mar 2014 Abstract. In the abstract Tile Assembly Model (atam),
Lecture 5: Pitch and Chord (1) Chord Recognition. Li Su
 Lecture 5: Pitch and Chord (1) Chord Recognition Li Su Recap: short-time Fourier transform Given a discrete-time signal x(t) sampled at a rate f s. Let window size N samples, hop size H samples, then the
Lecture 5: Pitch and Chord (1) Chord Recognition Li Su Recap: short-time Fourier transform Given a discrete-time signal x(t) sampled at a rate f s. Let window size N samples, hop size H samples, then the
REVIEW SHEET FOR MIDTERM 2: ADVANCED
 REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
Solving Problems by Searching
 Solving Problems by Searching Berlin Chen 2005 Reference: 1. S. Russell and P. Norvig. Artificial Intelligence: A Modern Approach. Chapter 3 AI - Berlin Chen 1 Introduction Problem-Solving Agents vs. Reflex
Solving Problems by Searching Berlin Chen 2005 Reference: 1. S. Russell and P. Norvig. Artificial Intelligence: A Modern Approach. Chapter 3 AI - Berlin Chen 1 Introduction Problem-Solving Agents vs. Reflex
Permutation Tableaux and the Dashed Permutation Pattern 32 1
 Permutation Tableaux and the Dashed Permutation Pattern William Y.C. Chen and Lewis H. Liu Center for Combinatorics, LPMC-TJKLC Nankai University, Tianjin, P.R. China chen@nankai.edu.cn, lewis@cfc.nankai.edu.cn
Permutation Tableaux and the Dashed Permutation Pattern William Y.C. Chen and Lewis H. Liu Center for Combinatorics, LPMC-TJKLC Nankai University, Tianjin, P.R. China chen@nankai.edu.cn, lewis@cfc.nankai.edu.cn
Section 7.2 Logarithmic Functions
 Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
Math 150 c Lynch 1 of 6 Section 7.2 Logarithmic Functions Definition. Let a be any positive number not equal to 1. The logarithm of x to the base a is y if and only if a y = x. The number y is denoted
10703 Deep Reinforcement Learning and Control
 10703 Deep Reinforcement Learning and Control Russ Salakhutdinov Slides borrowed from Katerina Fragkiadaki Solving known MDPs: Dynamic Programming Markov Decision Process (MDP)! A Markov Decision Process
10703 Deep Reinforcement Learning and Control Russ Salakhutdinov Slides borrowed from Katerina Fragkiadaki Solving known MDPs: Dynamic Programming Markov Decision Process (MDP)! A Markov Decision Process
Lecture 20 November 13, 2014
 6.890: Algorithmic Lower Bounds: Fun With Hardness Proofs Fall 2014 Prof. Erik Demaine Lecture 20 November 13, 2014 Scribes: Chennah Heroor 1 Overview This lecture completes our lectures on game characterization.
6.890: Algorithmic Lower Bounds: Fun With Hardness Proofs Fall 2014 Prof. Erik Demaine Lecture 20 November 13, 2014 Scribes: Chennah Heroor 1 Overview This lecture completes our lectures on game characterization.
On game semantics of the affine and intuitionistic logics (Extended abstract)
 On game semantics of the affine and intuitionistic logics (Extended abstract) Ilya Mezhirov 1 and Nikolay Vereshchagin 2 1 The German Research Center for Artificial Intelligence, TU Kaiserslautern, ilya.mezhirov@dfki.uni-kl.de
On game semantics of the affine and intuitionistic logics (Extended abstract) Ilya Mezhirov 1 and Nikolay Vereshchagin 2 1 The German Research Center for Artificial Intelligence, TU Kaiserslautern, ilya.mezhirov@dfki.uni-kl.de
Pinpointing Computation with Modular Queries in the Boolean Hierarchy
 Pinpointing Computation with Modular Queries in the Boolean Hierarchy Manindra Agrawal Richard Beigel Thomas Thierauf Abstract A modular query consists of asking how many (modulo m) of k strings belong
Pinpointing Computation with Modular Queries in the Boolean Hierarchy Manindra Agrawal Richard Beigel Thomas Thierauf Abstract A modular query consists of asking how many (modulo m) of k strings belong
Game-playing AIs: Games and Adversarial Search I AIMA
 Game-playing AIs: Games and Adversarial Search I AIMA 5.1-5.2 Games: Outline of Unit Part I: Games as Search Motivation Game-playing AI successes Game Trees Evaluation Functions Part II: Adversarial Search
Game-playing AIs: Games and Adversarial Search I AIMA 5.1-5.2 Games: Outline of Unit Part I: Games as Search Motivation Game-playing AI successes Game Trees Evaluation Functions Part II: Adversarial Search
Extensive Form Games: Backward Induction and Imperfect Information Games
 Extensive Form Games: Backward Induction and Imperfect Information Games CPSC 532A Lecture 10 October 12, 2006 Extensive Form Games: Backward Induction and Imperfect Information Games CPSC 532A Lecture
Extensive Form Games: Backward Induction and Imperfect Information Games CPSC 532A Lecture 10 October 12, 2006 Extensive Form Games: Backward Induction and Imperfect Information Games CPSC 532A Lecture
Equivalence classes of length-changing replacements of size-3 patterns
 Equivalence classes of length-changing replacements of size-3 patterns Vahid Fazel-Rezai Mentor: Tanya Khovanova 2013 MIT-PRIMES Conference May 18, 2013 Vahid Fazel-Rezai Length-Changing Pattern Replacements
Equivalence classes of length-changing replacements of size-3 patterns Vahid Fazel-Rezai Mentor: Tanya Khovanova 2013 MIT-PRIMES Conference May 18, 2013 Vahid Fazel-Rezai Length-Changing Pattern Replacements
PROPORTIONAL VERSUS NONPROPORTIONAL RELATIONSHIPS NOTES
 PROPORTIONAL VERSUS NONPROPORTIONAL RELATIONSHIPS NOTES Proportional means that if x is changed, then y is changed in the same proportion. This relationship can be expressed by a proportional/linear function
PROPORTIONAL VERSUS NONPROPORTIONAL RELATIONSHIPS NOTES Proportional means that if x is changed, then y is changed in the same proportion. This relationship can be expressed by a proportional/linear function
From Fibonacci to Catalan permutations
 PUMA Vol 7 (2006), No 2, pp 7 From Fibonacci to Catalan permutations E Barcucci Dipartimento di Sistemi e Informatica, Università di Firenze, Viale G B Morgagni 65, 5034 Firenze - Italy e-mail: barcucci@dsiunifiit
PUMA Vol 7 (2006), No 2, pp 7 From Fibonacci to Catalan permutations E Barcucci Dipartimento di Sistemi e Informatica, Università di Firenze, Viale G B Morgagni 65, 5034 Firenze - Italy e-mail: barcucci@dsiunifiit
arxiv: v2 [cs.ds] 5 Apr 2016
![arxiv: v2 [cs.ds] 5 Apr 2016 arxiv: v2 [cs.ds] 5 Apr 2016](/thumbs/77/75872179.jpg) A Discrete and Bounded Envy-Free Cake Cutting Protocol for Four Agents Haris Aziz Simon Mackenzie Data61 and UNSW Sydney, Australia {haris.aziz, simon.mackenzie}@data61.csiro.au arxiv:1508.05143v2 [cs.ds]
A Discrete and Bounded Envy-Free Cake Cutting Protocol for Four Agents Haris Aziz Simon Mackenzie Data61 and UNSW Sydney, Australia {haris.aziz, simon.mackenzie}@data61.csiro.au arxiv:1508.05143v2 [cs.ds]
Game Theory and Algorithms Lecture 19: Nim & Impartial Combinatorial Games
 Game Theory and Algorithms Lecture 19: Nim & Impartial Combinatorial Games May 17, 2011 Summary: We give a winning strategy for the counter-taking game called Nim; surprisingly, it involves computations
Game Theory and Algorithms Lecture 19: Nim & Impartial Combinatorial Games May 17, 2011 Summary: We give a winning strategy for the counter-taking game called Nim; surprisingly, it involves computations
Sets. Gazihan Alankuş (Based on original slides by Brahim Hnich et al.) August 6, Outline Sets Equality Subset Empty Set Cardinality Power Set
 Gazihan Alankuş (Based on original slides by Brahim Hnich et al.) August 6, 2012 Gazihan Alankuş (Based on original slides by Brahim Hnich et al.) Gazihan Alankuş (Based on original slides by Brahim Hnich
Gazihan Alankuş (Based on original slides by Brahim Hnich et al.) August 6, 2012 Gazihan Alankuş (Based on original slides by Brahim Hnich et al.) Gazihan Alankuş (Based on original slides by Brahim Hnich
JMG. Review Module 1 Lessons 1-20 for Mid-Module. Prepare for Endof-Unit Assessment. Assessment. Module 1. End-of-Unit Assessment.
 Lesson Plans Lesson Plan WEEK 161 December 5- December 9 Subject to change 2016-2017 Mrs. Whitman 1 st 2 nd Period 3 rd Period 4 th Period 5 th Period 6 th Period H S Mathematics Period Prep Geometry Math
Lesson Plans Lesson Plan WEEK 161 December 5- December 9 Subject to change 2016-2017 Mrs. Whitman 1 st 2 nd Period 3 rd Period 4 th Period 5 th Period 6 th Period H S Mathematics Period Prep Geometry Math
Compulsory Exercise no. 1 Deadline: 1 May 2014
 Side 1 hans@phys.au.dk 6 April 014 Compulsory Exercise no. 1 Deadline: 1 May 014 The goal of the present compulsory exercise is to construct software that can be used for time series analysis. In order
Side 1 hans@phys.au.dk 6 April 014 Compulsory Exercise no. 1 Deadline: 1 May 014 The goal of the present compulsory exercise is to construct software that can be used for time series analysis. In order
