Georgia Standards of Excellence Frameworks. Mathematics. Accelerated GSE Pre-Calculus Unit 4: Trigonometric Identities
|
|
|
- Bernice Barker
- 5 years ago
- Views:
Transcription
1 Georgia Standards of Excellence Frameworks Mathematics Accelerated GSE Pre-Calculus Unit 4: Trigonometric Identities These materials are for nonprofit educational purposes only. Any other use may constitute copyright infringement.
2 Unit 4 Trigonometric Identities Table of Contents OVERVIEW... 3 STANDARDS ADDRESSED IN THIS UNIT... 3 KEY STANDARDS... 3 STANDARDS FOR MATHEMATICAL PRACTICE... 3 ENDURING UNDERSTANDINGS... 4 ESSENTIAL QUESTIONS... 4 CONCEPTS/SKILLS TO MAINTAIN... 4 SELECTED TERMS AND SYMBOLS... 5 CLASSROOM ROUTINES... 6 STRATEGIES FOR TEACHING AND LEARNING... 6 EVIDENCE OF LEARNING... 7 TASKS... 7 PROVING THE SINE ADDITION AND SUBTRACTION IDENTITIES... 8 PROVING THE COSINE ADDITION AND SUBTRACTION IDENTITIES A DISTANCE FORMULA PROOF FOR THE COSINE ADDITION IDENTITY PROVING THE TANGENT ADDITION AND SUBTRACTION IDENTITIES DOUBLE-ANGLE IDENTITIES FOR SINE, COSINE, AND TANGENT THE COSINE DOUBLE-ANGLE: A MAN WITH MANY IDENTITIES DERIVING HALF-ANGLE IDENTITIES CULMINATING TASK: HOW MANY ANGLES CAN YOU FIND? *Revised standards indicated in bold red font. July 2015 Page 2 of 49
3 OVERVIEW In this unit, students will: build upon their work with trigonometric identities with addition and subtraction formulas will look at addition and subtraction formulas geometrically prove addition and subtraction formulas use addition and subtraction formulas to solve problems Although the units in this instructional framework emphasize key standards and big ideas at specific times of the year, routine topics such as estimation, mental computation, and basic computation facts should be addressed on an ongoing basis. Ideas related to the eight practice standards should be addressed constantly as well. To assure that this unit is taught with the appropriate emphasis, depth, and rigor, it is important that the tasks listed under Evidence of Learning be reviewed early in the planning process. A variety of resources should be utilized to supplement this unit. This unit provides much needed content information, but excellent learning activities as well. The tasks in this unit illustrate the types of learning activities that should be utilized from a variety of sources. STANDARDS ADDRESSED IN THIS UNIT Mathematical standards are interwoven and should be addressed throughout the year in as many different units and activities as possible in order to emphasize the natural connections that exist among mathematical topics. The standards call for a student to demonstrate mastery of the content by proving these addition and subtraction formulas using various methods. KEY STANDARDS Prove and apply trigonometric identities MGSE9-12.F.TF.9 Prove addition, subtraction, double, and half-angle formulas for sine, cosine, and tangent and use them to solve problems. STANDARDS FOR MATHEMATICAL PRACTICE Refer to the Comprehensive Course Overview for more detailed information about the Standards for Mathematical Practice. 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively. 3. Construct viable arguments and critique the reasoning of others. July 2015 Page 3 of 49
4 4. Model with mathematics. 5. Use appropriate tools strategically. 6. Attend to precision. 7. Look for and make use of structure. Georgia Department of Education 8. Look for and express regularity in repeated reasoning. ENDURING UNDERSTANDINGS Understand the concept of identity Prove the addition formula for sine, cosine and tangent Prove the subtraction formula for sine, cosine and tangent Use trigonometric functions to prove formulas ESSENTIAL QUESTIONS How can I add trigonometric functions? How can I subtract trigonometric functions? How can I prove the addition formula for trigonometric functions? How can I prove the subtraction formula for trigonometric functions? What is an identity? CONCEPTS/SKILLS TO MAINTAIN It is expected that students will have prior knowledge/experience related to the concepts and skills identified below. It may be necessary to pre-assess in order to determine if time needs to be spent on conceptual activities that help students develop a deeper understanding of these ideas. number sense computation with whole numbers and decimals, including application of order of operations applications of the Pythagorean Theorem operations with trigonometric ratios operations with radians and degrees even and odd functions geometric constructions algebraic proofs geometric proofs methods of proof July 2015 Page 4 of 49
5 SELECTED TERMS AND SYMBOLS Georgia Department of Education The following terms and symbols are often misunderstood. These concepts are not an inclusive list and should not be taught in isolation. However, due to evidence of frequent difficulty and misunderstanding associated with these concepts, instructors should pay particular attention to them and how their students are able to explain and apply them. The definitions below are for teacher reference only and are not to be memorized by the students. Students should explore these concepts using models and real life examples. Students should understand the concepts involved and be able to recognize and/or demonstrate them with words, models, pictures, or numbers. The website below is interactive and includes a math glossary. Definitions and activities for these and other terms can be found on the Intermath website. Links to external sites are particularly useful. Addition Identity for Cosine: cos( x+ y) = cos xcos y sin xsin y Addition Identity for Sine: sin( x+ y) = sin xcos y+ cos xsin y tan x+ tan y Addition Identity for Tangent: tan( x+ y) = 1 tan xtan y Double Angle Identity for Sine: sin(2x) = 2 sin x cos x Double Angle Identity for Cosine: cos(2x) = cos 2 x sin 2 x = 2 cos 2 x 1 = 1 2 sin 2 x 2 tan x Double Angle Identity for Tangent: tan 2x = Half Angle Identity for Sine: sin x x = ± 1 cos tan 2 x Half Angle Identity for Cosine: cos x cos x = ± Half Angle Identity for Tangent: tan x x = ± 1 cos = sin x 1 cos x = 2 1+cos x 1+cos x sin x Even Function: a function with symmetry about the y-axis that satisfies the relationship f( x) = f( x) Identity: an identity is a relation that is always true, no matter the value of the variable. Odd Function: a function with symmetry about the origin that satisfies the relationship f( x) = f( x) Subtraction Identity for Cosine: cos( x y) = cos xcos y+ sin xsin y Subtraction Identity for Sine: sin( x y) = sin xcos y cos xsin y tan x tan y Subtraction Identity for Tangent: tan( x y) = 1 + tan xtan y July 2015 Page 5 of 49
6 CLASSROOM ROUTINES Georgia Department of Education The importance of continuing the established classroom routines cannot be overstated. Daily routines must include such obvious activities as estimating, analyzing data, describing patterns, and answering daily questions. They should also include less obvious routines, such as how to select materials, how to use materials in a productive manner, how to put materials away, how to access classroom technology such as computers and calculators. An additional routine is to allow plenty of time for children to explore new materials before attempting any directed activity with these new materials. The regular use of routines is important to the development of students' number sense, flexibility, fluency, collaborative skills and communication. These routines contribute to a rich, hands-on standards based classroom and will support students performances on the tasks in this unit and throughout the school year. STRATEGIES FOR TEACHING AND LEARNING Students should be actively engaged by developing their own understanding. Mathematics should be represented in as many ways as possible by using graphs, tables, pictures, symbols and words. Interdisciplinary and cross curricular strategies should be used to reinforce and extend the learning activities. Appropriate manipulatives and technology should be used to enhance student learning. Students should be given opportunities to revise their work based on teacher feedback, peer feedback, and metacognition which includes self-assessment and reflection. Students should write about the mathematical ideas and concepts they are learning. Consideration of all students should be made during the planning and instruction of this unit. Teachers need to consider the following: What level of support do my struggling students need in order to be successful with this unit? In what way can I deepen the understanding of those students who are competent in this unit? What real life connections can I make that will help my students utilize the skills practiced in this unit? July 2015 Page 6 of 49
7 EVIDENCE OF LEARNING Georgia Department of Education By the conclusion of this unit, students should be able to demonstrate the following competencies: Demonstrate a method to prove addition or subtraction identities for sine, cosine, and tangent. Apply addition or subtraction identities for sine, cosine, and tangent. Use addition or subtraction identities to find missing values for sine, cosine and tangent functions. TASKS The following tasks represent the level of depth, rigor, and complexity expected of all Pre- Calculus students. These tasks or tasks of similar depth and rigor should be used to demonstrate evidence of learning. It is important that all elements of a task be addressed throughout the learning process so that students understand what is expected of them. While some tasks are identified as a performance task, they may also be used for teaching and learning (learning task). Task Name Proving the Sine Addition and Subtraction Identities Proving the Cosine Addition and Subtraction Identities A Distance Formula Proof for the Cosine Addition Identity Proving the Tangent Addition and Subtraction Identities Double Angle Identities for Sine, Cosine, and Tangent. The Cosine Double- Angle Half Angle Identities for Sine, Cosine, and Tangent Culminating Task: How Many Angles Can You Find? Task Type Grouping Strategy Learning Task Large Group/Partner Task Learning Task Large Group/Partner Task Learning Task Individual/Partner Task Learning Task Partner/Small Group Task Learning Task Individual/Partner Learning Task Individual/Partner Learning Task Individual/Partner Performance Task Individual/Partner Task Content Addressed Developing a proof for the Sine addition and subtraction identities. Developing a proof for the Cosine addition and subtraction identities. Using the Distance Formula to develop a proof for the Cosine addition identity. Developing a proof for the Tangent addition and subtraction identities. Using the Addition Identities to Derive the Double Angle Identities Exploring the different forms of and uses for the double angle identity for cosine. Using the Double Angle Identities to Derive the Half Angle Identities Using trigonometric addition and subtraction identities to determine trigonometric values. July 2015 Page 7 of 49
8 PROVING THE SINE ADDITION AND SUBTRACTION IDENTITIES Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double, and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: This task guides students through one possible proof of addition and subtraction identities for sine. It is designed to guide the student step by step through the process, with several stops along the way to make sure they are on the right track. The emphasis should not be on this particular method, but rather the act of proof itself. Ask students to look beyond the steps to see mathematics happening through proof. PROVING THE SINE ADDITION AND SUBTRACTION IDENTITIES When it becomes necessary to add and subtract angles, finding the sine of the new angles is not as straight forward as adding or subtracting the sine of the individual angles. Convince yourself of this by performing the following operation: sin(30 + ) sin(60 = ) sin(90 )? In this task, you will develop a formula for finding the sine of a sum or difference of two angles. Begin by looking at the diagram below. (note: DG AB ): Use the diagram to answer the following questions: July 2015 Page 8 of 49
9 D E C F A x y G 90 B 1. What type of triangles are AAA, AAA aaa DDD? Right Triangles 2. Write an expression for the measurement of DAB. m DAB = x + y 3. Write an expression forsin DAB. sin( x+ y) = DG AD 4. EG BC Now we will use algebra to develop the formula for the sine of a sum of two angles. July 2015 Page 9 of 49
10 a. Use your expression from #3. sin( x+ y) = DG AD b. Rewrite DG as the sum of two segments, EG and DE, then split the fraction. DG EG + DE EG DE sin( x+ y) = = = + AD AD AD AD c. Use the relationship from #4 to make a substitution. EG DE BC DE sin( x+ y) = + = + AD AD AD AD BC DE Did you arrive at this equation? sin( x+ y) = + If not, go back and try again. AD AD a. Now multiply the first term by AC CD, and the second term by. This will not change AC CD the value of our expressions, but will establish a link between some important pieces. BC AC DE CD sin( x+ y) = + AD AC AD CD We are using AC and CD because they give us sine and cosine ratios when we multiply and divide them purposefully in each term. b. Now change the order on the denominators of both terms. BC AC DE CD sin( x+ y) = + AC AD CD AD BC AC DE CD Did you arrive at this equation? sin( x+ y) = + AC AD CD AD July 2015 Page 10 of 49
11 Now is the most important step. Look at each factor. What relationship do each of those represent? For example, BC is the opposite side from X, and AC is the hypotenuse in that BC triangle. This means that sin X AC =. Substitute the other values and you have developed a formula for sin(x+y). Students may have trouble finding a substitution for DE. Try to point them towards the fact CD that triangle CDE and triangle FCE are similar(ce is parallel to AB so angle ECA is congruent to angle BAC by alternate interior angles.) BC AC DE CD sin( x+ y) = + = sin xcos y+ cos xsin y AC AD CD AD Check your formula with the following exercises: 1. sin( ) = sin(90 )? sin 45 cos 45 + cos 45 sin 45 = + = 1 = sin sin π π sin π + =? π π π π π sin cos + cos sin = + = 1 = sin Write your formula here: sin( x+ y) = sin xcos y+ cos xsin y Now that we have a formula for the sine of a sum of angles, we can use it to develop the formula for the difference of angles. We can think of the difference of two angles like this: sin( x y) = sin( x+ ( y)) Using the formula we developed above, we substitute in and get: sin( x y) = sin xcos( y) + cos xsin( y) July 2015 Page 11 of 49
12 But, cosine is an even function meaning that: f( x) = f( x). Use this fact to simplify the equation. sin( x y) = sin xcos y+ cos xsin( y) Similarly, sine is an odd function meaning that: f( x) = f( x). Use this fact to simplify the equation. sin( x y) = sin xcos y cos xsin y Write your formula here: sin( x y) = sin xcos y cos xsin y A note to the teacher: This task only involves proving the addition and subtraction identities. The classroom teacher should build on this proof by providing problems that build competency and fluency in applying the identity. Such problems should include, but not be limited to: finding exact values, expressing as a trigonometric function of one angle, verifying identities and solving trigonometric equations. July 2015 Page 12 of 49
13 PROVING THE SINE ADDITION AND SUBTRACTION IDENTITIES When it becomes necessary to add and subtract angles, finding the sine of the new angles is not as straight forward as adding or subtracting the sine of the individual angles. Convince yourself of this by performing the following operation: sin(30 + ) sin(60 = ) sin(90 )? In this task, you will develop a formula for finding the sine of a sum or difference of two angles. Begin by looking at the diagram below. (note: DG AB ): D E C F A x y G 90 B Use the diagram to answer the following questions: 1. What type of triangles are AAA, AAA aaa DDD? 2. Write an expression for the measurement of DAB. July 2015 Page 13 of 49
14 3. Write an expression forsin DAB. 4. EG Now we will use algebra to develop the formula for the sine of a sum of two angles. a. Use your expression from #3. b. Rewrite DG as the sum of two segments, EG and DE, then split the fraction. c. Use the relationship from #4 to make a substitution. BC DE Did you arrive at this equation? sin( x+ y) = + If not, go back and try again. AD AD a. Now multiply the first term by AC CD, and the second term by. This will not change AC CD the value of our expressions, but will establish a link between some important pieces. b. Now change the order on the denominators of both terms. BC AC DE CD Did you arrive at this equation? sin( x+ y) = + AC AD CD AD July 2015 Page 14 of 49
15 Now is the most important step. Look at each factor. What relationship do each of those represent? For example, BC is the opposite side from X, and AC is the hypotenuse in that BC triangle. This means that sin X AC =. Substitute the other values and you have developed a formula for sin(x+y). Check your formula with the following exercises: 1. sin( ) = sin(90 )? 2. sin π π sin π + =? Write your formula here: Now that we have a formula for the sine of a sum of angles, we can use it to develop the formula for the difference of angles. We can think of the difference of two angles like this: sin( x y) = sin( x+ ( y)) Using the formula we developed above, we substitute in and get: sin( x y) = sin xcos( y) + cos xsin( y) But, cosine is an even function meaning that: f( x) = f( x). Use this fact to simplify the equation. Similarly, sine is an odd function meaning that: f( x) = f( x). Use this fact to simplify the equation. Write your formula here: July 2015 Page 15 of 49
16 PROVING THE COSINE ADDITION AND SUBTRACTION IDENTITIES Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: This task follows the format of the first task. It is designed to guide the student step by step through the process, with several stops along the way to make sure they are on the right track. The emphasis should not be on this particular method, but rather the act of proof itself. Ask students to look beyond the steps to see mathematics happening through proof. PROVING THE COSINE ADDITION AND SUBTRACTION IDENTITIES In the first task you saw that it is necessary to develop a formula for calculating the sine of sums or differences of angles. Can the same formula work for cosine? Experiment with your formula and see if you can use it to answer the exercise below: cos(30 + ) cos(60 = ) cos(90 )? In this task, you will develop a formula for finding the sine of a sum or difference of two angles. Begin by looking at the diagram below. (note: DG AB ): July 2015 Page 16 of 49
17 D E C F A x y G 90 B Use the diagram to answer the following questions: 1. What type of triangles are AAA, AAA aaa DDD? Right Triangles 2. Write an expression for the measurement of DAB. m DAB = x + y 3. Write an expression for cos DAB. cos( x+ y) = AG DA 4. BG EC July 2015 Page 17 of 49
18 5. ECA CAB by alternate interior angles. 6. CDE ECA because they are corresponding angles in similar triangles. Now we will use algebra to develop the formula for the cosine of a sum of two angles. a. Use your expression from #3. cos( x+ y) = AG DA b. Rewrite AG as the difference of two segments, AB and BG, then split the fraction. AG AB BG AB BG cos( x+ y) = = = DA AD AD AD c. Use the relationship from #4 to make a substitution. AB EC cos( x+ y) = AD AD AB EC Did you arrive at this equation? cos( x+ y) = If not, go back and try again. AD AD a. Now multiply the first term by AC CD, and the second term by. This will not change AC CD the value of our expressions, but will establish a link between some important pieces. AB AC EC CD cos( x+ y) = AD AC AD CD We are using AC and CD because they give us sine and cosine ratios when we multiply and divide them purposefully in each term. b. Now change the order on the denominators of both terms. July 2015 Page 18 of 49
19 AB AC EC CD cos( x+ y) = AC AD CD AD AB AC EC CD Did you arrive at this equation? cos( x+ y) = AC AD CD AD Now is the most important step. Look at each factor. What relationship do each of those represent? For example, EC is the opposite side from X (from similarity), and CD is a EC hypotenuse in that triangle. This means that sin X CD =. Substitute the other values and you have developed a formula for cos(x+y). cos( x+ y) = cos x cos y sin x sin y Check your formula with the following exercises: 1. cos( ) = cos(60 )? cos( ) = cos 30 cos 30 sin 30 sin 30 = = = cos cos π π cos π + =? π π π π π π π cos( + ) = cos cos sin sin = = 0 = cos Write your formula here: cos( x+ y) = cos x cos y sin x sin y Now that we have a formula for the cosine of a sum of angles, we can use it to develop the formula for the difference of angles. We can think of the difference of two angles like this: cos( x y) = cos( x+ ( y)) Using the formula we developed above, we substitute in and get: cos( x y) = cos xcos( y) sin xsin( y) July 2015 Page 19 of 49
20 But, cosine is an even function meaning that: f( x) = f( x). Use this fact to simplify the equation. cos( x y) = cos x cos y sin x sin ( y) Similarly, sine is an odd function meaning that: f( x) = f( x). Use this fact to simplify the equation. cos( x y) = cos x cos y+ sin x sin y Write your formula here: cos( x y) = cos x cos y+ sin x sin y A note to the teacher: This task only involves proving the addition and subtraction identities. The classroom teacher should build on this proof by providing problems that build competency and fluency in applying the identity. Such problems should include, but not be limited to: finding exact values, expressing as a trigonometric function of one angle, verifying identities and solving trigonometric equations. July 2015 Page 20 of 49
21 PROVING THE COSINE ADDITION AND SUBTRACTION IDENTITIES In the first task you saw that it is necessary to develop a formula for calculating the sine of sums or differences of angles. Can the same formula work for cosine? Experiment with your formula and see if you can use it to answer the exercise below: cos(30 + ) cos(60 = ) cos(90 )? In this task, you will develop a formula for finding the sine of a sum or difference of two angles. Begin by looking at the diagram below. (note: DG AB ): D E C F A x y G 90 B Use the diagram to answer the following questions: July 2015 Page 21 of 49
22 1. What type of triangles are AAA, AAA aaa DDD? 2. Write an expression for the measurement of DAB. 3. Write an expression for cos DAB. 4. BG 5. ECA by alternate interior angles. 6. CDE because they are corresponding angles in similar triangles. Now we will use algebra to develop the formula for the cosine of a sum of two angles. a. Use your expression from #3. b. Rewrite AG as the difference of two segments, AB and BG, then split the fraction. c. Use the relationship from #4 to make a substitution. AB EC Did you arrive at this equation? cos( x+ y) = If not, go back and try again. AD AD a. Now multiply the first term by AC CD, and the second term by. This will not change AC CD the value of our expressions, but will establish a link between some important pieces. b. Now change the order on the denominators of both terms. July 2015 Page 22 of 49
23 AB AC EC CD Did you arrive at this equation? cos( x+ y) = AC AD CD AD Now is the most important step. Look at each factor. What relationship do each of those represent? For example, EC is the opposite side from X (from similarity), and CD is a EC hypotenuse in that triangle. This means that sin X CD =. Substitute the other values and you have developed a formula for cos(x+y). Check your formula with the following exercises: 1. cos( ) = cos(60 )? 2. cos π π cos π + =? Write your formula here: Now that we have a formula for the cosine of a sum of angles, we can use it to develop the formula for the difference of angles. We can think of the difference of two angles like this: cos( x y) = cos( x+ ( y)) Using the formula we developed above, we substitute in and get: cos( x y) = cos xcos( y) sin xsin( y) But, cosine is an even function meaning that: f( x) = f( x). Use this fact to simplify the equation. July 2015 Page 23 of 49
24 Similarly, sine is an odd function meaning that: f( x) = f( x). Use this fact to simplify the equation. Write your formula here: July 2015 Page 24 of 49
25 A DISTANCE FORMULA PROOF FOR THE COSINE ADDITION IDENTITY Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: In this task, students derive the sum identity for the cosine function, in the process reviewing some of the geometric topics and ideas about proofs. This derivation also provides practice with algebraic manipulation of trigonometric functions that include examples of how applying the Pythagorean identities can often simplify a cumbersome trigonometric expression. Rewriting expressions in order to solve trigonometric equations is one of the more common applications of the sum and difference identities. This task is presented as an alternative proof to the ones the students performed earlier. A DISTANCE FORMULA PROOF FOR THE COSINE ADDITION IDENTITY In this task, you will use the sum and difference identities to solve equations and find the exact values of angles that are not multiples of π and π. Before you apply these identities to 6 4 problems, you will first derive them. The first identity you will prove involves taking the cosine of the sum of two angles. ( ) cos α + β = cosαcos β sinαsin β We can derive this identity by making deductions from the relationships between the quantities on the unit circle below. July 2015 Page 25 of 49
26 R Q O β α -β P S 1. Complete the following congruence statements: a. ROP QOS b. RO QO PO SO c. By the SAS congruence theorem, ROP QOS d. RP QS 2. Write the coordinates of each of the four points on the unit circle, remembering that the cosine and sine functions produce x- and y- values on the unit circle. a. R = ( cos( α + β), sin ( α β) + ) b. Q = ( cos α,sinα ) c. P = (1, 0) ( ) d. S = cos ( β),sin ( β) July 2015 Page 26 of 49
27 3. Use the coordinates found in problem 2 and the distance formula to find the length of chord RP. Note: Students may not simplify here, but will need to in part 5. Solution: ( ) ( cos α + β 1) + ( sin ( α + β) 0) 2 2 = cos 2 ( α β) 2 cos( α β) 1 sin 2 ( α β) = ( ( α β) sin 2 ( α β) ) 1 2 cos ( α β) = cos( α + β) applying a Pythagorean identity = 2 2cos( α + β) squaring each binomial rearranging terms 4. a. Use the coordinates found in problem 2 and the distance formula to find the length of chord QS. Note: Students may not simplify here, but will need to in part 5. Solution: ( ) ( cosα cos( β) ) + sinα sin ( β) 2 2 = cos 2 α 2 cosα cos ( β) cos 2 ( β) sin 2 α 2sinα sin ( β) sin 2 ( β) squaring each binomial = ( cos 2 α + sin 2 α) + ( cos 2 ( β) + sin 2 ( β) ) 2 cosα cos ( β) 2sinα sin ( β) rearranging terms cosα cos β 2sinα sin β applying a Pythagorean identity twice = ( ) ( ) = 2 2 cosα cos( β) 2sinα sin ( β) b. Two useful identities that you may choose to explore later are cos( θ ) sin( θ ) sinθ July 2015 Page 27 of 49 = cosθ and =. Use these two identities to simplify your solution to 4a so that your expression has no negative angles. Solution: 2 2 cosα cos( β) 2sinα sin ( β) = 2 2 cosα cos β 2sinα( sin β) = 2 2 cosα cos β + 2sinα sin β 5. From 1d, you know that RP QS. You can therefore write an equation by setting the expressions found in problems 3 and 4b equal to one another. Simplify this equation and
28 solve for cos( α β) Georgia Department of Education +. Applying one of the Pythagorean Identities will be useful! When finished, you will have derived the angle sum identity for cosine. Solution: ( ) ( ) ( ) 2 2 cos α + β = 2 2 cosα cos β + 2sinα sin β 2 2 cos α + β = 2 2 cosα cos β + 2sinα sin β squaring both sides 2 cos α + β = 2 cosα cos β + 2sinα sin β adding 2 to both sides cos(α ± β) = cos α cos β sin α sin β dividing both sides by 2 The other three sum and difference identities can be derived from the identity found in problem 5. These four identities can be summarized with the following two statements. ( ) sin α ± β = sinα cos β ± cosα sin β cos(α ± β) = cos α cos β sin α sin β Recall that so far, you can only calculate the exact values of the sines and cosines of multiples of π and π. These identities will allow you to calculate the exact value of the sine and 6 4 cosine of many more angles. 6. Evaluate sin 75 by applying the angle addition identity for sine and evaluating each trigonometric function: Solution: sin( )= sin 30 cos 45 + cos 30 sin = + = July 2015 Page 28 of 49
29 7. Similarly, find the exact value of the following trigonometric expressions: a. cos 15 ( ) Solution: π b. sin 12 Solution: c. cos(345 ) Solution: d. 19π sin 12 Solution: July 2015 Page 29 of 49
30 A DISTANCE FORMULA PROOF FOR THE COSINE ADDITION IDENTITY In this task, you will use the sum and difference identities to solve equations and find the exact values of angles that are not multiples of π and π. Before you apply these identities to 6 4 problems, you will first derive them. The first identity you will prove involves taking the cosine of the sum of two angles. ( ) cos α + β = cosαcos β sinαsin β We can derive this identity by making deductions from the relationships between the quantities on the unit circle below. R Q O β α -β P S 1. Complete the following congruence statements: a. ROP b. RO c. By the congruence theorem, ROP QOS d. RP July 2015 Page 30 of 49
31 2. Write the coordinates of each of the four points on the unit circle, remembering that the cosine and sine functions produce x- and y- values on the unit circle. a. R = b. Q = c. P = d. S = 3. Use the coordinates found in problem 2 and the distance formula to find the length of chord RP. 4. Use the coordinates found in problem 2 and the distance formula to find the length of chordqs. 5. From 1d, you know that RP QS. You can therefore write an equation by setting the expressions found in problems 3 and 4b equal to one another. Simplify this equation and cos α + β. Applying one of the Pythagorean Identities will be useful! When solve for ( ) finished, you will have derived the angle sum identity for cosine. July 2015 Page 31 of 49
32 The other three sum and difference identities can be derived from the identity found in problem 5. These four identities can be summarized with the following two statements. ( ) ( ) sin α ± β = sinα cos β ± cosα sin β cos α ± β = cosα cos β sinα sin β Recall that so far, you can only calculate the exact values of the sines and cosines of multiples of π and π. These identities will allow you to calculate the exact value of the sine and 6 4 cosine of many more angles. 6. Evaluate sin 75 by applying the angle addition identity for sine and evaluating each trigonometric function: sin( )= sin 30 cos 45 + cos 30 sin Similarly, find the exact value of the following trigonometric expressions: a. cos 15 ( ) π b. sin 12 c. cos(345 ) d. 19π sin 12 July 2015 Page 32 of 49
33 PROVING THE TANGENT ADDITION AND SUBTRACTION IDENTITIES Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: This task uses algebraic manipulation and the previously developed identities to derive tangent addition and subtraction identities. Again, the emphasis should be on the mathematical processes and not the method itself. Students should feel confident in manipulating algebraic expressions and simplifying trigonometric expressions using identities. PROVING THE TANGENT ADDITION AND SUBTRACTION IDENTITIES By this point, you should have developed formulas for sine and cosine of sums and differences of angles. If so, you are already most of the way to finding a formula for the tangent of a sum of two angles. Let s begin with a relationship that we already know to be true about tangent. 1. tan x sin x cos x = so it stands to reason that tan ( x y) + = sin( x+ y ) cos( x+ y) Use what you already know about sum and difference formulas to expand the relationship above. 2. tan ( x y) + = sin xcos y+ cos xsin y cos xcos y sin xsin y July 2015 Page 33 of 49
34 1 3. Now we want to simplify this. (Hint: Multiply numerator and denominator by cos x ) 1 The reason to multiply by is to establish a tangent ratio and to divide out cos x. It is cos x important that students see why to choose that value as a part of the proof. sin xcos y cos xsin y + cos cos tan cos sin tan( ) x x x y+ y x+ y = = cos xcos y sin xsin y cos y tan xsin y cos x cos x 4. You can simplify it some more. Think about step 3 for a hint. 1 Students should multiply by to establish a tangent ratio for the y variable and cos y divide out cos y. Lead them back to #3 if they need help. tan xcos y sin y + cos y cos y tan x+ tan y tan( x+ y) = = cos y tan xsin y 1 tan xtan y cos y cos y 5. Write your formula here for the tangent of a sum: tan x+ tan y tan( x+ y) = 1 tan xtan y 6. Now that you have seen the process, develop a formula for the tangent of a difference. Encourage students to attempt this on their own without referring back to the proof of the addition identity. If they need help, they may reference it. Encourage them to persevere through this process and not give up easily. Mathematics and especially proof is meant to be a productive struggle in which students work hard to construct their own knowledge. When they have finished, they should have: tan x tan y tan( x y) = 1 + tan xtan y July 2015 Page 34 of 49
35 Write your formula here: tan x tan y tan( x y) = 1 + tan xtan y July 2015 Page 35 of 49
36 THE TANGENT ADDITION AND SUBTRACTION IDENTITIES By this point, you should have developed formulas for sine and cosine of sums and differences of angles. If so, you are already most of the way to finding a formula for the tangent of a sum of two angles. Let s begin with a relationship that we already know to be true about tangent. 1. tan x sin x cos x = so it stands to reason that tan ( x y) + = Use what you already know about sum and difference formulas to expand the relationship above. 2. tan ( x y) + = 3. Now we want to simplify this. (Hint: Multiply numerator and denominator by 1 cos x ) 4. You can simplify it some more. Think about step 3 for a hint. 5. Write your formula here for the tangent of a sum: 6. Now that you have seen the process, develop a formula for the tangent of a difference. Write your formula here: July 2015 Page 36 of 49
37 6b. Georgia Department of Education DOUBLE-ANGLE IDENTITIES FOR SINE, COSINE, AND TANGENT Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double, and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: This task guides students through a derivation of the double-angle identities for the primary trigonometric functions. It also aims to draw a distinction between doubling an angle and doubling the value of a trigonometric function associated with that angle. This distinction is a common misunderstanding that students have. The task concentrates on the derivation of the sine double-angle formula by leading the students through a step-by-step process. The students are then left to derive the cosine and tangent identities through the use of the same process. DOUBLE-ANGLE IDENTITIES FOR SINE, COSINE, AND TANGENT Before we begin Evaluate the following expressions without a calculator. 1a. cos 45 = 2/2 1b. cos 90 = 0 2a. sin 60 = 3/22T 2b. sin 120 = 3/2 3a. sin π 6 = 1/22T 3b. sin π 3 = 3/2 4a. cos π = 0 4b. cos π= 1 2 5a. tan 5π 6 = 3/32T 5b. tan 5π 3 = 3 6a. tan 45 = 12T tan 90 = undefined2t Study the expressions in parts a and b of the problems above they are related. Describe how the expressions in parts a and b of the problems differ. The angle measures in parts b are twice the measure of the angles in parts a. Consider the following Based on the observations above decide which of these statements are keepers & which are trash. July 2015 Page 37 of 49
38 If an angle is doubled then the sine value of the angle is doubled too. If an angle is halved then the cosine value of the angle is halved too. 2 sin x sin 2x Double the angle & double the sine value really mean the same thing. The equation 2 cos x = cos 2x has no solutions. Doubling angles does not double their trig values. One more thing Before we go on, let s look at the graph above can you identify the two equations that have been graphed? Write them on opposite sides of the equals sign below. 2 cos x cos 2x = Discussion questions: Is the equation above an identity? Does the equation above have solutions? Does the graph above change your opinion of any of the keepers or trash on the previous page? Let s Dig In! Hopefully it is obvious to you by now that if an angle is doubled, we know very little about what happens to its trig values. One thing we are certain of, however, is that doubling an angle does not double its trig values (except in some special cases!). Try this: You are familiar, by now, with the identity sin(x + y) = sin x cos y + cos x sin y. A - In the space below, rewrite the identity replacing both x and y with x. July 2015 Page 38 of 49
39 sin(x + x) = sin x cos x + cos x sin x B - Now, by combining like terms on the left side and like terms on the right side, simplify the identity you wrote above. sin(2x) = 2 sin x cos x C - Use the new mathematical identity you found to complete the following statement. The words to the right may be helpful. To find the sine value of an angle that I ve doubled, I can double the product of the sine value and the cosine value sine cosine sum product double half identity value argument Now, on a separate paper, repeat A - B - C - for cosine and tangent! July 2015 Page 39 of 49
40 DOUBLE-ANGLE IDENTITIES FOR SINE, COSINE, AND TANGENT Before we begin Evaluate the following expressions without a calculator. 1a. cos 45 = 1b. cos 90 = 2a. sin 60 = 2b. sin 120 = 3a. sin π 6 = 3b. sin π 3 = 4a. cos π = 2 4b. cos π= 5a. tan 5π = 6 5b. tan 5π = 3 6a. tan 45 = 6b. tan 90 = Study the expressions in parts a and b of the problems above they are related. Describe how the expressions in parts a and b of the problems differ. Consider the following Based on the observations above decide which of these statements are keepers & which are trash. If an angle is doubled then the sine value of the angle is doubled too. If an angle is halved then the cosine value of the angle is halved too. 2 sin x sin 2x Double the angle & double the sine value really mean the same thing. The equation 2 cos x = cos 2x has no solutions. Doubling angles does not double their trig values. July 2015 Page 40 of 49
41 One more thing Before we go on, let s look at the graph above can you identify the two equations that have been graphed? Write them on opposite sides of the equals sign below. = Discussion questions: Is the equation above an identity? Does the equation above have solutions? Does the graph above change your opinion of any of the keepers or trash on the previous page? Let s Dig In! Hopefully it is obvious to you by now that if an angle is doubled, we know very little about what happens to its trig values. One thing we are certain of, however, is that doubling an angle does not double its trig values (except in some special cases!). Try this: You are familiar, by now, with the identity sin(x + y) = sin x cos y + cos x sin y. A - In the space below, rewrite the identity replacing both x and y with xs. B - Now, by combining like terms on the left side and like terms on the right side, simplify the identity you wrote above. C - Use the new mathematical identity you found to complete the following statement. The words to the right may be helpful. To find the sine value of an angle that I ve doubled, I can sine cosine sum product double half identity value argument Now, on a separate paper, repeat A - B - C - for cosine and tangent! July 2015 Page 41 of 49
42 THE COSINE DOUBLE-ANGLE: A MAN WITH MANY IDENTITIES Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double, and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: This task serves as a discovery of the alternate forms of the cosine double angle identity and also as a segue into the next task (deriving half-angle identities). A discussion about the advantages of the two alternate forms is encouraged. There is an extension included that challenges students to derive the double angle identity for tangent using the double angle identity for sine and cosine. The Cosine Double-Angle: A man with many identities. Verify these two identities: cos 2 x sin 2 x = 2 cos 2 x 1 cos 2 x sin 2 x = 2 cos 2 x (sin 2 x + cos 2 x) cos 2 x sin 2 x = 2 cos 2 x sin 2 x cos 2 x cos 2 x sin 2 x = 2 cos 2 x cos 2 x sin 2 x cos 2 x sin 2 x = cos 2 x sin 2 x cos 2 x sin 2 x = 1 2 sin 2 x cos 2 x sin 2 x = (sin 2 x + cos 2 x) 2 sin 2 x cos 2 x sin 2 x = sin 2 x + cos 2 x 2 sin 2 x cos 2 x sin 2 x = cos 2 x +sin 2 x 2 sin 2 x cos 2 x sin 2 x = cos 2 x sin 2 x Earlier, you discovered that cos(2x) = cos 2 x sin 2 x. Use the transitive property of equality along with the identities above to rewrite two alternate forms of the double angle identity for cosine. cos(2x) = cos 2 x sin 2 x or cos(2x) = 2 cos 2 x 1 or cos(2x) = 1 2 sin 2 x July 2015 Page 42 of 49
43 Discussion Question: What advantages might one of the two alternate forms of the identity have over the original? Answers Vary: the two alternate forms express the double-angle identity for sine in terms of only one trig function instead of two. Try this! You have written a double-angle identity for tangent already (based off the sum identity). Try sin 2x simplifying tan 2x = to get the same thing. A helpful hint: You ll want to, at some point in cos 2x the process, divide the top and bottom by cos 2 x tan 2x = tan 2x = tan 2x = tan 2x = tan 2x = sin 2x cos 2x 2 sin x cos x cos 2 x sin 2 x 2 sin x cos x cos 2 x cos 2 x sin 2 x cos 2 x 2 sin x cos x cos 2 x cos 2 x sin2 x cos 2 x 2 tan x 1 tan 2 x July 2015 Page 43 of 49
44 The Cosine Double-Angle: A Man With Many Identities Verify these two identities: cos 2 x sin 2 x = 2 cos 2 x 1 cos 2 x sin 2 x = 1 2 sin 2 x Earlier, you discovered that cos(2x) = cos 2 x sin 2 x. Use the transitive property of equality along with the identities above to rewrite two alternate forms of the double angle identity for cosine. cos(2x) = cos 2 x sin 2 x or cos(2x) = or cos(2x) = Discussion Question: What advantages might one of the two alternate forms of the identity have over the original? Try this! You have written a double-angle identity for tangent already (based off the sum identity). Try sin 2x simplifying tan 2x = to get the same thing. A helpful hint: You ll want to, at some point in cos 2x the process, divide the top and bottom by July 2015 Page 44 of 49
45 DERIVING HALF-ANGLE IDENTITIES Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double, and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: This task leads students through the derivation of the half-angle identities. It emphasizes algebraic manipulation and substitution as a means to transform a known identity into an identity that is more useful for a particular purpose. The opportunity to present math as a tool that has been created and can be manipulated by people is one that should not be missed by the teacher. It is recommended that students have completed the two tasks previous to this one. DERIVING HALF-ANGLE IDENTITIES After deriving the double-angle identities for sine, cosine, and tangent, you re ready to try the same for half-angle identities. To do so, you ll use the double-angle identities you just derived. Follow these steps to find a half-angle identity. 1. Begin with either of the alternate forms of the cosine double-angle identity. Notice that, in the alternate identities, there are two instances of the variable x one that is x alone and the other that is 2x. cos 2x = 2 cos 2 x 1 cos 2x = 1 2 sin 2 x 2. Rearrange your chosen identity so that the term with x alone gets isolated on a side. Think about this question: If you wanted to evaluate angle x for the trig function you isolated, what information would you need to know in order to use the identity you have? cos 2x = 2 cos 2 x 1 cos 2x = 1 2 sin 2 x 1 + cos 2x cos x = ± 2 1 cos 2x sin x = ± 2 We d like to have something more useful that what came out of step 2. We d like an identity that will give us the trig function value of half an angle if we know a trig function value of the full angle. We can do this with a simple substitution. 3. Into the result you have from step 2 above, substitute u for x. Now simplify the result. Record 2 your result below. July 2015 Page 45 of 49
46 Half-Angle Identity for Sine Half-Angle Identity for Cosine Half-Angle Identity for Tangent sin u x =± 1 cos cos u x =± 1+cos tan u x =± 1 cos 2 1+cos x 4. After step 3, you have one of the three identities above. Now, return to step 1 and choose a different alternate form. Complete steps 2 and 3 again. Record the other identity in the correct place above. 5. Finally, there s tangent. It has been tricky in past identity sets (e.g. sums, differences, and double-angle) but is it surprisingly easy to come up with a working identity for tan u 2. Verify this identity (there are three here) and discuss your findings with a classmate: sin x 1 + cos x = ± 1 cos x 1 + cos x = 1 cos x sin x This triple identity has three parts. The middle member of this identity is the half angle identity for tangent that was derived above. The two members on either side of the identity above are alternate forms of the half angle identity for tangent. Students could work through any one of these three identities above but should not miss the fact that alternate forms of the half angle identity for tangent are being verified. July 2015 Page 46 of 49
47 DERIVING HALF-ANGLE IDENTITIES After deriving the double-angle identities for sine, cosine, and tangent, you re ready to try the same for half-angle identities. To do so, you ll use the double-angle identities you just derived. Follow these steps to find a half-angle identity. 1. Begin with either of the alternate forms of the cosine double-angle identity. Notice that, in the alternate identities, there are two instances of the variable x one that is x alone and the other that is 2x. 2. Rearrange your chosen identity so that the term with x alone gets isolated on a side. Think about this question: If you wanted to evaluate angle x for the trig function you isolated, what information would you need to know in order to use the identity you have? We d like to have something more useful that what came out of step 2. We d like an identity that will give us the trig function value of half an angle if we know a trig function value of the full angle. We can do this with a simple substitution. 3. Into the result you have from step 2 above, substitute u for x. Now simplify the result. Record 2 your result below. Half-Angle Identity for Sine Half-Angle Identity for Cosine Half-Angle Identity for Tangent sin u 2 =± cos u 2 =± tan u 2 =± 4. After step 3, you have one of the three identities above. Now, return to step 1 and choose a different alternate form. Complete steps 2 and 3 again. Record the other identity in the correct place above. 5. Finally, there s tangent. It has been tricky in past identity sets (e.g. sums, differences, and double-angle) but is it surprisingly easy to come up with a working identity for tan u 2. Verify this identity (there are three here) and discuss your findings with a classmate: sin x 1 + cos x = ± 1 cos x 1 + cos x = 1 cos x sin x July 2015 Page 47 of 49
48 CULMINATING TASK: HOW MANY ANGLES CAN YOU FIND? Georgia Standards of Excellence: MGSE9-12.F.TF.9 Prove addition, subtraction, double and half-angle formulas for sine, cosine, and tangent and use them to solve problems. Introduction: The purpose of this culminating task is to give students an exercise in using the identities that they have developed. There are many possibilities for answers and students should demonstrate that they can apply each of the identities with other trigonometric relationships in order to find the answers. You may consider suggesting different methods for students who need more guidance. For example, find 2 angles using the sine addition identity etc. CULMINATING TASK: HOW MANY ANGLES CAN YOU FIND? Using the following values, how many other trigonometric values of angles between 0 and 180 degrees can you find (without using a calculator)? Don t forget about complementary angles, co-terminal angles and other trig rules. Show work and justification for each value. sin 5 = ; cos 45 = ; sin 60 = ; cos 60 = 0.5 Example: sin 50 = sin( ) = sin 5 cos 45 + cos 5 sin 45 and remembering that sin cos 2 5 = 1 allows us to find cos 5 = , so sin 50 = (0.7071) (0.9962) = (which is quite close to the actual value of ). EXTENSION: Have students develop an identity for sin(x+y+z), cos(x+y+z) and tan(x+y+z). July 2015 Page 48 of 49
49 CULMINATING TASK: HOW MANY ANGLES CAN YOU FIND? Using the following values, how many other trigonometric values of angles between 0 and 180 degrees can you find (without using a calculator)? Don t forget about complementary angles, co-terminal angles and other trig rules. Show work and justification for each value. sin 5 = ; cos 45 = ; sin 60 = ; cos 60 = 0.5 July 2015 Page 49 of 49
Double-Angle, Half-Angle, and Reduction Formulas
 Double-Angle, Half-Angle, and Reduction Formulas By: OpenStaxCollege Bicycle ramps for advanced riders have a steeper incline than those designed for novices. Bicycle ramps made for competition (see [link])
Double-Angle, Half-Angle, and Reduction Formulas By: OpenStaxCollege Bicycle ramps for advanced riders have a steeper incline than those designed for novices. Bicycle ramps made for competition (see [link])
Exactly Evaluating Even More Trig Functions
 Exactly Evaluating Even More Trig Functions Pre/Calculus 11, Veritas Prep. We know how to find trig functions of certain, special angles. Using our unit circle definition of the trig functions, as well
Exactly Evaluating Even More Trig Functions Pre/Calculus 11, Veritas Prep. We know how to find trig functions of certain, special angles. Using our unit circle definition of the trig functions, as well
P1 Chapter 10 :: Trigonometric Identities & Equations
 P1 Chapter 10 :: Trigonometric Identities & Equations jfrost@tiffin.kingston.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 20 th August 2017 Use of DrFrostMaths for practice Register for free
P1 Chapter 10 :: Trigonometric Identities & Equations jfrost@tiffin.kingston.sch.uk www.drfrostmaths.com @DrFrostMaths Last modified: 20 th August 2017 Use of DrFrostMaths for practice Register for free
Trigonometric identities
 Trigonometric identities An identity is an equation that is satisfied by all the values of the variable(s) in the equation. For example, the equation (1 + x) = 1 + x + x is an identity. If you replace
Trigonometric identities An identity is an equation that is satisfied by all the values of the variable(s) in the equation. For example, the equation (1 + x) = 1 + x + x is an identity. If you replace
Trigonometry. An Overview of Important Topics
 Trigonometry An Overview of Important Topics 1 Contents Trigonometry An Overview of Important Topics... 4 UNDERSTAND HOW ANGLES ARE MEASURED... 6 Degrees... 7 Radians... 7 Unit Circle... 9 Practice Problems...
Trigonometry An Overview of Important Topics 1 Contents Trigonometry An Overview of Important Topics... 4 UNDERSTAND HOW ANGLES ARE MEASURED... 6 Degrees... 7 Radians... 7 Unit Circle... 9 Practice Problems...
Chapter 3, Part 1: Intro to the Trigonometric Functions
 Haberman MTH 11 Section I: The Trigonometric Functions Chapter 3, Part 1: Intro to the Trigonometric Functions In Example 4 in Section I: Chapter, we observed that a circle rotating about its center (i.e.,
Haberman MTH 11 Section I: The Trigonometric Functions Chapter 3, Part 1: Intro to the Trigonometric Functions In Example 4 in Section I: Chapter, we observed that a circle rotating about its center (i.e.,
How to Do Trigonometry Without Memorizing (Almost) Anything
 How to Do Trigonometry Without Memorizing (Almost) Anything Moti en-ari Weizmann Institute of Science http://www.weizmann.ac.il/sci-tea/benari/ c 07 by Moti en-ari. This work is licensed under the reative
How to Do Trigonometry Without Memorizing (Almost) Anything Moti en-ari Weizmann Institute of Science http://www.weizmann.ac.il/sci-tea/benari/ c 07 by Moti en-ari. This work is licensed under the reative
Trigonometry Review Page 1 of 14
 Trigonometry Review Page of 4 Appendix D has a trigonometric review. This material is meant to outline some of the proofs of identities, help you remember the values of the trig functions at special values,
Trigonometry Review Page of 4 Appendix D has a trigonometric review. This material is meant to outline some of the proofs of identities, help you remember the values of the trig functions at special values,
Georgia Performance Standards Framework for Mathematics Grade 6 Unit Seven Organizer: SCALE FACTOR (3 weeks)
 The following instructional plan is part of a GaDOE collection of Unit Frameworks, Performance Tasks, examples of Student Work, and Teacher Commentary. Many more GaDOE approved instructional plans are
The following instructional plan is part of a GaDOE collection of Unit Frameworks, Performance Tasks, examples of Student Work, and Teacher Commentary. Many more GaDOE approved instructional plans are
Year 10 Term 1 Homework
 Yimin Math Centre Year 10 Term 1 Homework Student Name: Grade: Date: Score: Table of contents 6 Year 10 Term 1 Week 6 Homework 1 6.1 Triangle trigonometry................................... 1 6.1.1 The
Yimin Math Centre Year 10 Term 1 Homework Student Name: Grade: Date: Score: Table of contents 6 Year 10 Term 1 Week 6 Homework 1 6.1 Triangle trigonometry................................... 1 6.1.1 The
Lesson 27: Sine and Cosine of Complementary and Special Angles
 Lesson 7 M Classwork Example 1 If α and β are the measurements of complementary angles, then we are going to show that sin α = cos β. In right triangle ABC, the measurement of acute angle A is denoted
Lesson 7 M Classwork Example 1 If α and β are the measurements of complementary angles, then we are going to show that sin α = cos β. In right triangle ABC, the measurement of acute angle A is denoted
Module 5 Trigonometric Identities I
 MAC 1114 Module 5 Trigonometric Identities I Learning Objectives Upon completing this module, you should be able to: 1. Recognize the fundamental identities: reciprocal identities, quotient identities,
MAC 1114 Module 5 Trigonometric Identities I Learning Objectives Upon completing this module, you should be able to: 1. Recognize the fundamental identities: reciprocal identities, quotient identities,
MHF4U. Advanced Functions Grade 12 University Mitchell District High School. Unit 4 Radian Measure 5 Video Lessons
 MHF4U Advanced Functions Grade 12 University Mitchell District High School Unit 4 Radian Measure 5 Video Lessons Allow no more than 1 class days for this unit! This includes time for review and to write
MHF4U Advanced Functions Grade 12 University Mitchell District High School Unit 4 Radian Measure 5 Video Lessons Allow no more than 1 class days for this unit! This includes time for review and to write
3.2 Proving Identities
 3.. Proving Identities www.ck.org 3. Proving Identities Learning Objectives Prove identities using several techniques. Working with Trigonometric Identities During the course, you will see complex trigonometric
3.. Proving Identities www.ck.org 3. Proving Identities Learning Objectives Prove identities using several techniques. Working with Trigonometric Identities During the course, you will see complex trigonometric
Mathematics Lecture. 3 Chapter. 1 Trigonometric Functions. By Dr. Mohammed Ramidh
 Mathematics Lecture. 3 Chapter. 1 Trigonometric Functions By Dr. Mohammed Ramidh Trigonometric Functions This section reviews the basic trigonometric functions. Trigonometric functions are important because
Mathematics Lecture. 3 Chapter. 1 Trigonometric Functions By Dr. Mohammed Ramidh Trigonometric Functions This section reviews the basic trigonometric functions. Trigonometric functions are important because
Math 1205 Trigonometry Review
 Math 105 Trigonometry Review We begin with the unit circle. The definition of a unit circle is: x + y =1 where the center is (0, 0) and the radius is 1. An angle of 1 radian is an angle at the center of
Math 105 Trigonometry Review We begin with the unit circle. The definition of a unit circle is: x + y =1 where the center is (0, 0) and the radius is 1. An angle of 1 radian is an angle at the center of
Trigonometry. David R. Wilkins
 Trigonometry David R. Wilkins 1. Trigonometry 1. Trigonometry 1.1. Trigonometric Functions There are six standard trigonometric functions. They are the sine function (sin), the cosine function (cos), the
Trigonometry David R. Wilkins 1. Trigonometry 1. Trigonometry 1.1. Trigonometric Functions There are six standard trigonometric functions. They are the sine function (sin), the cosine function (cos), the
cos 2 x + sin 2 x = 1 cos(u v) = cos u cos v + sin u sin v sin(u + v) = sin u cos v + cos u sin v
 Concepts: Double Angle Identities, Power Reducing Identities, Half Angle Identities. Memorized: cos x + sin x 1 cos(u v) cos u cos v + sin v sin(u + v) cos v + cos u sin v Derive other identities you need
Concepts: Double Angle Identities, Power Reducing Identities, Half Angle Identities. Memorized: cos x + sin x 1 cos(u v) cos u cos v + sin v sin(u + v) cos v + cos u sin v Derive other identities you need
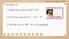
MATH 1040 CP 15 SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question.
 MATH 1040 CP 15 SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. 1) (sin x + cos x) 1 + sin x cos x =? 1) ) sec 4 x + sec x tan x - tan 4 x =? ) ) cos
MATH 1040 CP 15 SHORT ANSWER. Write the word or phrase that best completes each statement or answers the question. 1) (sin x + cos x) 1 + sin x cos x =? 1) ) sec 4 x + sec x tan x - tan 4 x =? ) ) cos
One of the classes that I have taught over the past few years is a technology course for
 Trigonometric Functions through Right Triangle Similarities Todd O. Moyer, Towson University Abstract: This article presents an introduction to the trigonometric functions tangent, cosecant, secant, and
Trigonometric Functions through Right Triangle Similarities Todd O. Moyer, Towson University Abstract: This article presents an introduction to the trigonometric functions tangent, cosecant, secant, and
Honors Algebra 2 w/ Trigonometry Chapter 14: Trigonometric Identities & Equations Target Goals
 Honors Algebra w/ Trigonometry Chapter 14: Trigonometric Identities & Equations Target Goals By the end of this chapter, you should be able to Identify trigonometric identities. (14.1) Factor trigonometric
Honors Algebra w/ Trigonometry Chapter 14: Trigonometric Identities & Equations Target Goals By the end of this chapter, you should be able to Identify trigonometric identities. (14.1) Factor trigonometric
Chapter 4/5 Part 2- Trig Identities and Equations
 Chapter 4/5 Part 2- Trig Identities and Equations Lesson Package MHF4U Chapter 4/5 Part 2 Outline Unit Goal: By the end of this unit, you will be able to solve trig equations and prove trig identities.
Chapter 4/5 Part 2- Trig Identities and Equations Lesson Package MHF4U Chapter 4/5 Part 2 Outline Unit Goal: By the end of this unit, you will be able to solve trig equations and prove trig identities.
4.3. Trigonometric Identities. Introduction. Prerequisites. Learning Outcomes
 Trigonometric Identities 4.3 Introduction trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles. There are a very large number
Trigonometric Identities 4.3 Introduction trigonometric identity is a relation between trigonometric expressions which is true for all values of the variables (usually angles. There are a very large number
Math 3 Trigonometry Part 2 Waves & Laws
 Math 3 Trigonometry Part 2 Waves & Laws GRAPHING SINE AND COSINE Graph of sine function: Plotting every angle and its corresponding sine value, which is the y-coordinate, for different angles on the unit
Math 3 Trigonometry Part 2 Waves & Laws GRAPHING SINE AND COSINE Graph of sine function: Plotting every angle and its corresponding sine value, which is the y-coordinate, for different angles on the unit
Trigonometric Identities. Copyright 2017, 2013, 2009 Pearson Education, Inc.
 5 Trigonometric Identities Copyright 2017, 2013, 2009 Pearson Education, Inc. 1 5.5 Double-Angle Double-Angle Identities An Application Product-to-Sum and Sum-to-Product Identities Copyright 2017, 2013,
5 Trigonometric Identities Copyright 2017, 2013, 2009 Pearson Education, Inc. 1 5.5 Double-Angle Double-Angle Identities An Application Product-to-Sum and Sum-to-Product Identities Copyright 2017, 2013,
MATH STUDENT BOOK. 12th Grade Unit 5
 MATH STUDENT BOOK 12th Grade Unit 5 Unit 5 ANALYTIC TRIGONOMETRY MATH 1205 ANALYTIC TRIGONOMETRY INTRODUCTION 3 1. IDENTITIES AND ADDITION FORMULAS 5 FUNDAMENTAL TRIGONOMETRIC IDENTITIES 5 PROVING IDENTITIES
MATH STUDENT BOOK 12th Grade Unit 5 Unit 5 ANALYTIC TRIGONOMETRY MATH 1205 ANALYTIC TRIGONOMETRY INTRODUCTION 3 1. IDENTITIES AND ADDITION FORMULAS 5 FUNDAMENTAL TRIGONOMETRIC IDENTITIES 5 PROVING IDENTITIES
Mathematics UNIT FIVE Trigonometry II. Unit. Student Workbook. Lesson 1: Trigonometric Equations Approximate Completion Time: 4 Days
 Mathematics 0- Student Workbook Unit 5 Lesson : Trigonometric Equations Approximate Completion Time: 4 Days Lesson : Trigonometric Identities I Approximate Completion Time: 4 Days Lesson : Trigonometric
Mathematics 0- Student Workbook Unit 5 Lesson : Trigonometric Equations Approximate Completion Time: 4 Days Lesson : Trigonometric Identities I Approximate Completion Time: 4 Days Lesson : Trigonometric
MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question.
 Trigonometry Final Exam Study Guide Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The graph of a polar equation is given. Select the polar
Trigonometry Final Exam Study Guide Name MULTIPLE CHOICE. Choose the one alternative that best completes the statement or answers the question. The graph of a polar equation is given. Select the polar
Algebra2/Trig Chapter 10 Packet
 Algebra2/Trig Chapter 10 Packet In this unit, students will be able to: Convert angle measures from degrees to radians and radians to degrees. Find the measure of an angle given the lengths of the intercepted
Algebra2/Trig Chapter 10 Packet In this unit, students will be able to: Convert angle measures from degrees to radians and radians to degrees. Find the measure of an angle given the lengths of the intercepted
WARM UP. 1. Expand the expression (x 2 + 3) Factor the expression x 2 2x Find the roots of 4x 2 x + 1 by graphing.
 WARM UP Monday, December 8, 2014 1. Expand the expression (x 2 + 3) 2 2. Factor the expression x 2 2x 8 3. Find the roots of 4x 2 x + 1 by graphing. 1 2 3 4 5 6 7 8 9 10 Objectives Distinguish between
WARM UP Monday, December 8, 2014 1. Expand the expression (x 2 + 3) 2 2. Factor the expression x 2 2x 8 3. Find the roots of 4x 2 x + 1 by graphing. 1 2 3 4 5 6 7 8 9 10 Objectives Distinguish between
2. Be able to evaluate a trig function at a particular degree measure. Example: cos. again, just use the unit circle!
 Study Guide for PART II of the Fall 18 MAT187 Final Exam NO CALCULATORS are permitted on this part of the Final Exam. This part of the Final exam will consist of 5 multiple choice questions. You will be
Study Guide for PART II of the Fall 18 MAT187 Final Exam NO CALCULATORS are permitted on this part of the Final Exam. This part of the Final exam will consist of 5 multiple choice questions. You will be
Math 123 Discussion Session Week 4 Notes April 25, 2017
 Math 23 Discussion Session Week 4 Notes April 25, 207 Some trigonometry Today we want to approach trigonometry in the same way we ve approached geometry so far this quarter: we re relatively familiar with
Math 23 Discussion Session Week 4 Notes April 25, 207 Some trigonometry Today we want to approach trigonometry in the same way we ve approached geometry so far this quarter: we re relatively familiar with
You found trigonometric values using the unit circle. (Lesson 4-3)
 You found trigonometric values using the unit circle. (Lesson 4-3) LEQ: How do we identify and use basic trigonometric identities to find trigonometric values & use basic trigonometric identities to simplify
You found trigonometric values using the unit circle. (Lesson 4-3) LEQ: How do we identify and use basic trigonometric identities to find trigonometric values & use basic trigonometric identities to simplify
Trigonometric Integrals Section 5.7
 A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics Trigonometric Integrals Section 5.7 Dr. John Ehrke Department of Mathematics Spring 2013 Eliminating Powers From Trig Functions
A B I L E N E C H R I S T I A N U N I V E R S I T Y Department of Mathematics Trigonometric Integrals Section 5.7 Dr. John Ehrke Department of Mathematics Spring 2013 Eliminating Powers From Trig Functions
Algebra 2/Trigonometry Review Sessions 1 & 2: Trigonometry Mega-Session. The Unit Circle
 Algebra /Trigonometry Review Sessions 1 & : Trigonometry Mega-Session Trigonometry (Definition) - The branch of mathematics that deals with the relationships between the sides and the angles of triangles
Algebra /Trigonometry Review Sessions 1 & : Trigonometry Mega-Session Trigonometry (Definition) - The branch of mathematics that deals with the relationships between the sides and the angles of triangles
Trig functions are examples of periodic functions because they repeat. All periodic functions have certain common characteristics.
 Trig functions are examples of periodic functions because they repeat. All periodic functions have certain common characteristics. The sine wave is a common term for a periodic function. But not all periodic
Trig functions are examples of periodic functions because they repeat. All periodic functions have certain common characteristics. The sine wave is a common term for a periodic function. But not all periodic
Solutions to Exercises, Section 5.6
 Instructor s Solutions Manual, Section 5.6 Exercise 1 Solutions to Exercises, Section 5.6 1. For θ = 7, evaluate each of the following: (a) cos 2 θ (b) cos(θ 2 ) [Exercises 1 and 2 emphasize that cos 2
Instructor s Solutions Manual, Section 5.6 Exercise 1 Solutions to Exercises, Section 5.6 1. For θ = 7, evaluate each of the following: (a) cos 2 θ (b) cos(θ 2 ) [Exercises 1 and 2 emphasize that cos 2
The reciprocal identities are obvious from the definitions of the six trigonometric functions.
 The Fundamental Identities: (1) The reciprocal identities: csc = 1 sec = 1 (2) The tangent and cotangent identities: tan = cot = cot = 1 tan (3) The Pythagorean identities: sin 2 + cos 2 =1 1+ tan 2 =
The Fundamental Identities: (1) The reciprocal identities: csc = 1 sec = 1 (2) The tangent and cotangent identities: tan = cot = cot = 1 tan (3) The Pythagorean identities: sin 2 + cos 2 =1 1+ tan 2 =
MATH 1113 Exam 3 Review. Fall 2017
 MATH 1113 Exam 3 Review Fall 2017 Topics Covered Section 4.1: Angles and Their Measure Section 4.2: Trigonometric Functions Defined on the Unit Circle Section 4.3: Right Triangle Geometry Section 4.4:
MATH 1113 Exam 3 Review Fall 2017 Topics Covered Section 4.1: Angles and Their Measure Section 4.2: Trigonometric Functions Defined on the Unit Circle Section 4.3: Right Triangle Geometry Section 4.4:
In this section, you will learn the basic trigonometric identities and how to use them to prove other identities.
 4.6 Trigonometric Identities Solutions to equations that arise from real-world problems sometimes include trigonometric terms. One example is a trajectory problem. If a volleyball player serves a ball
4.6 Trigonometric Identities Solutions to equations that arise from real-world problems sometimes include trigonometric terms. One example is a trajectory problem. If a volleyball player serves a ball
What role does the central angle play in helping us find lengths of arcs and areas of regions within the circle?
 Middletown Public Schools Mathematics Unit Planning Organizer Subject Geometry Grade/Course 10 Unit 5 Circles and other Conic Sections Duration 16 instructional + 4 days for reteaching/enrichment Big Idea
Middletown Public Schools Mathematics Unit Planning Organizer Subject Geometry Grade/Course 10 Unit 5 Circles and other Conic Sections Duration 16 instructional + 4 days for reteaching/enrichment Big Idea
( x "1) 2 = 25, x 3 " 2x 2 + 5x "12 " 0, 2sin" =1.
 Unit Analytical Trigonometry Classwork A) Verifying Trig Identities: Definitions to know: Equality: a statement that is always true. example:, + 7, 6 6, ( + ) 6 +0. Equation: a statement that is conditionally
Unit Analytical Trigonometry Classwork A) Verifying Trig Identities: Definitions to know: Equality: a statement that is always true. example:, + 7, 6 6, ( + ) 6 +0. Equation: a statement that is conditionally
Chapter 1 and Section 2.1
 Chapter 1 and Section 2.1 Diana Pell Section 1.1: Angles, Degrees, and Special Triangles Angles Degree Measure Angles that measure 90 are called right angles. Angles that measure between 0 and 90 are called
Chapter 1 and Section 2.1 Diana Pell Section 1.1: Angles, Degrees, and Special Triangles Angles Degree Measure Angles that measure 90 are called right angles. Angles that measure between 0 and 90 are called
MAT187H1F Lec0101 Burbulla
 Spring 17 What Is A Parametric Curve? y P(x, y) x 1. Let a point P on a curve have Cartesian coordinates (x, y). We can think of the curve as being traced out as the point P moves along it. 3. In this
Spring 17 What Is A Parametric Curve? y P(x, y) x 1. Let a point P on a curve have Cartesian coordinates (x, y). We can think of the curve as being traced out as the point P moves along it. 3. In this
PROVING IDENTITIES TRIGONOMETRY 4. Dr Adrian Jannetta MIMA CMath FRAS INU0115/515 (MATHS 2) Proving identities 1/ 7 Adrian Jannetta
 PROVING IDENTITIES TRIGONOMETRY 4 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Proving identities / 7 Adrian Jannetta Proving an identity Proving an identity is a process which starts with the
PROVING IDENTITIES TRIGONOMETRY 4 INU05/55 (MATHS 2) Dr Adrian Jannetta MIMA CMath FRAS Proving identities / 7 Adrian Jannetta Proving an identity Proving an identity is a process which starts with the
Math 180 Chapter 6 Lecture Notes. Professor Miguel Ornelas
 Math 180 Chapter 6 Lecture Notes Professor Miguel Ornelas 1 M. Ornelas Math 180 Lecture Notes Section 6.1 Section 6.1 Verifying Trigonometric Identities Verify the identity. a. sin x + cos x cot x = csc
Math 180 Chapter 6 Lecture Notes Professor Miguel Ornelas 1 M. Ornelas Math 180 Lecture Notes Section 6.1 Section 6.1 Verifying Trigonometric Identities Verify the identity. a. sin x + cos x cot x = csc
1 Graphs of Sine and Cosine
 1 Graphs of Sine and Cosine Exercise 1 Sketch a graph of y = cos(t). Label the multiples of π 2 and π 4 on your plot, as well as the amplitude and the period of the function. (Feel free to sketch the unit
1 Graphs of Sine and Cosine Exercise 1 Sketch a graph of y = cos(t). Label the multiples of π 2 and π 4 on your plot, as well as the amplitude and the period of the function. (Feel free to sketch the unit
Trigonometric Identities. Copyright 2017, 2013, 2009 Pearson Education, Inc.
 5 Trigonometric Identities Copyright 2017, 2013, 2009 Pearson Education, Inc. 1 5.3 Sum and Difference Identities Difference Identity for Cosine Sum Identity for Cosine Cofunction Identities Applications
5 Trigonometric Identities Copyright 2017, 2013, 2009 Pearson Education, Inc. 1 5.3 Sum and Difference Identities Difference Identity for Cosine Sum Identity for Cosine Cofunction Identities Applications
Chapter 6: Periodic Functions
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a triangle, and related to points on a circle. We noticed how the x and y values
Math 102 Key Ideas. 1 Chapter 1: Triangle Trigonometry. 1. Consider the following right triangle: c b
 Math 10 Key Ideas 1 Chapter 1: Triangle Trigonometry 1. Consider the following right triangle: A c b B θ C a sin θ = b length of side opposite angle θ = c length of hypotenuse cosθ = a length of side adjacent
Math 10 Key Ideas 1 Chapter 1: Triangle Trigonometry 1. Consider the following right triangle: A c b B θ C a sin θ = b length of side opposite angle θ = c length of hypotenuse cosθ = a length of side adjacent
MATH Week 10. Ferenc Balogh Winter. Concordia University
 MATH 20 - Week 0 Ferenc Balogh Concordia University 2008 Winter Based on the textbook J. Stuart, L. Redlin, S. Watson, Precalculus - Mathematics for Calculus, 5th Edition, Thomson All figures and videos
MATH 20 - Week 0 Ferenc Balogh Concordia University 2008 Winter Based on the textbook J. Stuart, L. Redlin, S. Watson, Precalculus - Mathematics for Calculus, 5th Edition, Thomson All figures and videos
Calculus for the Life Sciences
 Calculus for the Life Sciences Lecture Notes Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego
Calculus for the Life Sciences Lecture Notes Joseph M. Mahaffy, jmahaffy@mail.sdsu.edu Department of Mathematics and Statistics Dynamical Systems Group Computational Sciences Research Center San Diego
Trigonometric Equations
 Chapter Three Trigonometric Equations Solving Simple Trigonometric Equations Algebraically Solving Complicated Trigonometric Equations Algebraically Graphs of Sine and Cosine Functions Solving Trigonometric
Chapter Three Trigonometric Equations Solving Simple Trigonometric Equations Algebraically Solving Complicated Trigonometric Equations Algebraically Graphs of Sine and Cosine Functions Solving Trigonometric
Figure 5.1. sin θ = AB. cos θ = OB. tan θ = AB OB = sin θ. sec θ = 1. cotan θ = 1
 5 Trigonometric functions Trigonometry is the mathematics of triangles. A right-angle triangle is one in which one angle is 90, as shown in Figure 5.1. The thir angle in the triangle is φ = (90 θ). Figure
5 Trigonometric functions Trigonometry is the mathematics of triangles. A right-angle triangle is one in which one angle is 90, as shown in Figure 5.1. The thir angle in the triangle is φ = (90 θ). Figure
Math 104 Final Exam Review
 Math 04 Final Exam Review. Find all six trigonometric functions of θ if (, 7) is on the terminal side of θ.. Find cosθ and sinθ if the terminal side of θ lies along the line y = x in quadrant IV.. Find
Math 04 Final Exam Review. Find all six trigonometric functions of θ if (, 7) is on the terminal side of θ.. Find cosθ and sinθ if the terminal side of θ lies along the line y = x in quadrant IV.. Find
Mathematics. 6 th Grade Unit 7: Rational Explorations: Numbers and their Opposites
 CCGPS Frameworks Student Edition Mathematics 6 th Grade Unit 7: Rational Explorations: Numbers and their Opposites These materials are for nonprofit educational purposes only. Any other use may constitute
CCGPS Frameworks Student Edition Mathematics 6 th Grade Unit 7: Rational Explorations: Numbers and their Opposites These materials are for nonprofit educational purposes only. Any other use may constitute
c) What is the ratio of the length of the side of a square to the length of its diagonal? Is this ratio the same for all squares? Why or why not?
 Tennessee Department of Education Task: Ratios, Proportions, and Similar Figures 1. a) Each of the following figures is a square. Calculate the length of each diagonal. Do not round your answer. Geometry/Core
Tennessee Department of Education Task: Ratios, Proportions, and Similar Figures 1. a) Each of the following figures is a square. Calculate the length of each diagonal. Do not round your answer. Geometry/Core
Special Right Triangles and Right Triangle Trigonometry
 Special Right Triangles and Right Triangle Trigonometry Reporting Category Topic Triangles Investigating special right triangles and right triangle trigonometry Primary SOL G.8 The student will solve real-world
Special Right Triangles and Right Triangle Trigonometry Reporting Category Topic Triangles Investigating special right triangles and right triangle trigonometry Primary SOL G.8 The student will solve real-world
Math 36 "Fall 08" 5.2 "Sum and Di erence Identities" * Find exact values of functions of rational multiples of by using sum and di erence identities.
 Math 36 "Fall 08" 5.2 "Sum and Di erence Identities" Skills Objectives: * Find exact values of functions of rational multiples of by using sum and di erence identities. * Develop new identities from the
Math 36 "Fall 08" 5.2 "Sum and Di erence Identities" Skills Objectives: * Find exact values of functions of rational multiples of by using sum and di erence identities. * Develop new identities from the
Unit Circle: Sine and Cosine
 Unit Circle: Sine and Cosine Functions By: OpenStaxCollege The Singapore Flyer is the world s tallest Ferris wheel. (credit: Vibin JK /Flickr) Looking for a thrill? Then consider a ride on the Singapore
Unit Circle: Sine and Cosine Functions By: OpenStaxCollege The Singapore Flyer is the world s tallest Ferris wheel. (credit: Vibin JK /Flickr) Looking for a thrill? Then consider a ride on the Singapore
Prerequisite Knowledge: Definitions of the trigonometric ratios for acute angles
 easures, hape & pace EXEMPLAR 28 Trigonometric Identities Objective: To explore some relations of trigonometric ratios Key Stage: 3 Learning Unit: Trigonometric Ratios and Using Trigonometry Materials
easures, hape & pace EXEMPLAR 28 Trigonometric Identities Objective: To explore some relations of trigonometric ratios Key Stage: 3 Learning Unit: Trigonometric Ratios and Using Trigonometry Materials
Deriving the General Equation of a Circle
 Deriving the General Equation of a Circle Standard Addressed in this Task MGSE9-12.G.GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square
Deriving the General Equation of a Circle Standard Addressed in this Task MGSE9-12.G.GPE.1 Derive the equation of a circle of given center and radius using the Pythagorean Theorem; complete the square
Module Guidance Document. Geometry Module 2
 Geometry Module 2 Topic A Scale Drawings 5 days Topic B Dilations 5 days Topic C Similarity and Dilations 15 days Topic D Applying Similarity to Right 7 days Triangles Topic D Trigonometry 13 days Just
Geometry Module 2 Topic A Scale Drawings 5 days Topic B Dilations 5 days Topic C Similarity and Dilations 15 days Topic D Applying Similarity to Right 7 days Triangles Topic D Trigonometry 13 days Just
#9: Fundamentals of Trigonometry, Part II
 #9: Fundamentals of Trigonometry, Part II November 1, 2008 do not panic. In the last assignment, you learned general definitions of the sine and cosine functions. This week, we will explore some of the
#9: Fundamentals of Trigonometry, Part II November 1, 2008 do not panic. In the last assignment, you learned general definitions of the sine and cosine functions. This week, we will explore some of the
Name: A Trigonometric Review June 2012
 Name: A Trigonometric Review June 202 This homework will prepare you for in-class work tomorrow on describing oscillations. If you need help, there are several resources: tutoring on the third floor of
Name: A Trigonometric Review June 202 This homework will prepare you for in-class work tomorrow on describing oscillations. If you need help, there are several resources: tutoring on the third floor of
Trigonometry LESSON ONE - Degrees and Radians Lesson Notes
 8 = 6 Trigonometry LESSON ONE - Degrees and Radians Example : Define each term or phrase and draw a sample angle. Angle in standard position. b) Positive and negative angles. Draw. c) Reference angle.
8 = 6 Trigonometry LESSON ONE - Degrees and Radians Example : Define each term or phrase and draw a sample angle. Angle in standard position. b) Positive and negative angles. Draw. c) Reference angle.
2009 A-level Maths Tutor All Rights Reserved
 2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents radians 3 sine, cosine & tangent 7 cosecant, secant & cotangent
2 This book is under copyright to A-level Maths Tutor. However, it may be distributed freely provided it is not sold for profit. Contents radians 3 sine, cosine & tangent 7 cosecant, secant & cotangent
13-1 Trigonometric Identities. Find the exact value of each expression if 0 < θ < If cot θ = 2, find tan θ. SOLUTION: 2. If, find cos θ.
 Find the exact value of each expression if 0 < θ < 90 1. If cot θ = 2, find tan θ. 2. If, find cos θ. Since is in the first quadrant, is positive. Thus,. 3. If, find sin θ. Since is in the first quadrant,
Find the exact value of each expression if 0 < θ < 90 1. If cot θ = 2, find tan θ. 2. If, find cos θ. Since is in the first quadrant, is positive. Thus,. 3. If, find sin θ. Since is in the first quadrant,
GREATER CLARK COUNTY SCHOOLS PACING GUIDE. Grade 4 Mathematics GREATER CLARK COUNTY SCHOOLS
 GREATER CLARK COUNTY SCHOOLS PACING GUIDE Grade 4 Mathematics 2014-2015 GREATER CLARK COUNTY SCHOOLS ANNUAL PACING GUIDE Learning Old Format New Format Q1LC1 4.NBT.1, 4.NBT.2, 4.NBT.3, (4.1.1, 4.1.2,
GREATER CLARK COUNTY SCHOOLS PACING GUIDE Grade 4 Mathematics 2014-2015 GREATER CLARK COUNTY SCHOOLS ANNUAL PACING GUIDE Learning Old Format New Format Q1LC1 4.NBT.1, 4.NBT.2, 4.NBT.3, (4.1.1, 4.1.2,
Section 6-3 Double-Angle and Half-Angle Identities
 6-3 Double-Angle and Half-Angle Identities 47 Section 6-3 Double-Angle and Half-Angle Identities Double-Angle Identities Half-Angle Identities This section develops another important set of identities
6-3 Double-Angle and Half-Angle Identities 47 Section 6-3 Double-Angle and Half-Angle Identities Double-Angle Identities Half-Angle Identities This section develops another important set of identities
Big Ideas Math: A Common Core Curriculum Geometry 2015 Correlated to Common Core State Standards for High School Geometry
 Common Core State s for High School Geometry Conceptual Category: Geometry Domain: The Number System G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment,
Common Core State s for High School Geometry Conceptual Category: Geometry Domain: The Number System G.CO.1 Know precise definitions of angle, circle, perpendicular line, parallel line, and line segment,
Chapter 2: Pythagoras Theorem and Trigonometry (Revision)
 Chapter 2: Pythagoras Theorem and Trigonometry (Revision) Paper 1 & 2B 2A 3.1.3 Triangles Understand a proof of Pythagoras Theorem. Understand the converse of Pythagoras Theorem. Use Pythagoras 3.1.3 Triangles
Chapter 2: Pythagoras Theorem and Trigonometry (Revision) Paper 1 & 2B 2A 3.1.3 Triangles Understand a proof of Pythagoras Theorem. Understand the converse of Pythagoras Theorem. Use Pythagoras 3.1.3 Triangles
Pre-Calculus Unit 3 Standards-Based Worksheet
 Pre-Calculus Unit 3 Standards-Based Worksheet District of Columbia Public Schools Mathematics STANDARD PCT.P.9. Derive and apply basic trigonometric identities (e.g., sin 2 θ+cos 2 θ= 1,tan 2 θ + 1 = sec
Pre-Calculus Unit 3 Standards-Based Worksheet District of Columbia Public Schools Mathematics STANDARD PCT.P.9. Derive and apply basic trigonometric identities (e.g., sin 2 θ+cos 2 θ= 1,tan 2 θ + 1 = sec
Getting Triggy With It
 Getting Triggy With It Date: 15 May 2013 Topic: Pythagorean Theorem and Trigonometric Ratios Class: Grade 9 Ability Level: Mixed Ability Teacher: Mr. Cyrus Alvarez LESSON OBJECTIVES: At the end of the
Getting Triggy With It Date: 15 May 2013 Topic: Pythagorean Theorem and Trigonometric Ratios Class: Grade 9 Ability Level: Mixed Ability Teacher: Mr. Cyrus Alvarez LESSON OBJECTIVES: At the end of the
Chapter 6: Periodic Functions
 Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a right triangle, and related to points on a circle. We noticed how the x and y
Chapter 6: Periodic Functions In the previous chapter, the trigonometric functions were introduced as ratios of sides of a right triangle, and related to points on a circle. We noticed how the x and y
MATH 1112 FINAL EXAM REVIEW e. None of these. d. 1 e. None of these. d. 1 e. None of these. e. None of these. e. None of these.
 I. State the equation of the unit circle. MATH 111 FINAL EXAM REVIEW x y y = 1 x+ y = 1 x = 1 x + y = 1 II. III. If 1 tan x =, find sin x for x in Quadrant IV. 1 1 1 Give the exact value of each expression.
I. State the equation of the unit circle. MATH 111 FINAL EXAM REVIEW x y y = 1 x+ y = 1 x = 1 x + y = 1 II. III. If 1 tan x =, find sin x for x in Quadrant IV. 1 1 1 Give the exact value of each expression.
SPIRIT 2.0 Lesson: How Far Am I Traveling?
 SPIRIT 2.0 Lesson: How Far Am I Traveling? ===============================Lesson Header ============================ Lesson Title: How Far Am I Traveling? Draft Date: June 12, 2008 1st Author (Writer):
SPIRIT 2.0 Lesson: How Far Am I Traveling? ===============================Lesson Header ============================ Lesson Title: How Far Am I Traveling? Draft Date: June 12, 2008 1st Author (Writer):
θ = = 45 What is the measure of this reference angle?
 OF GENERAL ANGLES Our method of using right triangles only works for acute angles. Now we will see how we can find the trig function values of any angle. To do this we'll place angles on a rectangular
OF GENERAL ANGLES Our method of using right triangles only works for acute angles. Now we will see how we can find the trig function values of any angle. To do this we'll place angles on a rectangular
7.1 INTRODUCTION TO PERIODIC FUNCTIONS
 7.1 INTRODUCTION TO PERIODIC FUNCTIONS *SECTION: 6.1 DCP List: periodic functions period midline amplitude Pg 247- LECTURE EXAMPLES: Ferris wheel, 14,16,20, eplain 23, 28, 32 *SECTION: 6.2 DCP List: unit
7.1 INTRODUCTION TO PERIODIC FUNCTIONS *SECTION: 6.1 DCP List: periodic functions period midline amplitude Pg 247- LECTURE EXAMPLES: Ferris wheel, 14,16,20, eplain 23, 28, 32 *SECTION: 6.2 DCP List: unit
13-1 Trigonometric Identities. Find the exact value of each expression if 0 < θ < If cot θ = 2, find tan θ. ANSWER: 2. If, find cos θ.
 Find the exact value of each expression if 0 < θ < 90 1. If cot θ = 2, find tan θ. 8. CCSS PERSEVERANCE When unpolarized light passes through polarized sunglass lenses, the intensity of the light is cut
Find the exact value of each expression if 0 < θ < 90 1. If cot θ = 2, find tan θ. 8. CCSS PERSEVERANCE When unpolarized light passes through polarized sunglass lenses, the intensity of the light is cut
Pythagorean Identity. Sum and Difference Identities. Double Angle Identities. Law of Sines. Law of Cosines
 Review for Math 111 Final Exam The final exam is worth 30% (150/500 points). It consists of 26 multiple choice questions, 4 graph matching questions, and 4 short answer questions. Partial credit will be
Review for Math 111 Final Exam The final exam is worth 30% (150/500 points). It consists of 26 multiple choice questions, 4 graph matching questions, and 4 short answer questions. Partial credit will be
Anthony Chan. September, Georgia Adult Education Conference
 Anthony Chan September, 2018 1 2018 Georgia Adult Education Conference Attendees will be able to: Make difficult math concepts simple and help their students discover math principles on their own. This
Anthony Chan September, 2018 1 2018 Georgia Adult Education Conference Attendees will be able to: Make difficult math concepts simple and help their students discover math principles on their own. This
Math 122: Final Exam Review Sheet
 Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
Exam Information Math 1: Final Exam Review Sheet The final exam will be given on Wednesday, December 1th from 8-1 am. The exam is cumulative and will cover sections 5., 5., 5.4, 5.5, 5., 5.9,.1,.,.4,.,
7.1 INTRODUCTION TO PERIODIC FUNCTIONS
 7.1 INTRODUCTION TO PERIODIC FUNCTIONS Ferris Wheel Height As a Function of Time The London Eye Ferris Wheel measures 450 feet in diameter and turns continuously, completing a single rotation once every
7.1 INTRODUCTION TO PERIODIC FUNCTIONS Ferris Wheel Height As a Function of Time The London Eye Ferris Wheel measures 450 feet in diameter and turns continuously, completing a single rotation once every
Unit 5 Investigating Trigonometry Graphs
 Mathematics IV Frameworks Student Edition Unit 5 Investigating Trigonometry Graphs 1 st Edition Table of Contents INTRODUCTION:... 3 What s Your Temperature? Learning Task... Error! Bookmark not defined.
Mathematics IV Frameworks Student Edition Unit 5 Investigating Trigonometry Graphs 1 st Edition Table of Contents INTRODUCTION:... 3 What s Your Temperature? Learning Task... Error! Bookmark not defined.
Exercise 1. Consider the following figure. The shaded portion of the circle is called the sector of the circle corresponding to the angle θ.
 1 Radian Measures Exercise 1 Consider the following figure. The shaded portion of the circle is called the sector of the circle corresponding to the angle θ. 1. Suppose I know the radian measure of the
1 Radian Measures Exercise 1 Consider the following figure. The shaded portion of the circle is called the sector of the circle corresponding to the angle θ. 1. Suppose I know the radian measure of the
Analytic Geometry/ Trigonometry
 Analytic Geometry/ Trigonometry Course Numbers 1206330, 1211300 Lake County School Curriculum Map Released 2010-2011 Page 1 of 33 PREFACE Teams of Lake County teachers created the curriculum maps in order
Analytic Geometry/ Trigonometry Course Numbers 1206330, 1211300 Lake County School Curriculum Map Released 2010-2011 Page 1 of 33 PREFACE Teams of Lake County teachers created the curriculum maps in order
While you wait: For a-d: use a calculator to evaluate: Fill in the blank.
 While you wait: For a-d: use a calculator to evaluate: a) sin 50 o, cos 40 o b) sin 25 o, cos65 o c) cos o, sin 79 o d) sin 83 o, cos 7 o Fill in the blank. a) sin30 = cos b) cos57 = sin Trigonometric
While you wait: For a-d: use a calculator to evaluate: a) sin 50 o, cos 40 o b) sin 25 o, cos65 o c) cos o, sin 79 o d) sin 83 o, cos 7 o Fill in the blank. a) sin30 = cos b) cos57 = sin Trigonometric
5-5 Multiple-Angle and Product-to-Sum Identities
 Find the values of sin 2, cos 2, tan 2 1 cos for the given value interval, (270, 360 ) Since on the interval (270, 360 ), one point on the terminal side of θ has x-coordinate 3 a distance of 5 units from
Find the values of sin 2, cos 2, tan 2 1 cos for the given value interval, (270, 360 ) Since on the interval (270, 360 ), one point on the terminal side of θ has x-coordinate 3 a distance of 5 units from
Unit 8 Trigonometry. Math III Mrs. Valentine
 Unit 8 Trigonometry Math III Mrs. Valentine 8A.1 Angles and Periodic Data * Identifying Cycles and Periods * A periodic function is a function that repeats a pattern of y- values (outputs) at regular intervals.
Unit 8 Trigonometry Math III Mrs. Valentine 8A.1 Angles and Periodic Data * Identifying Cycles and Periods * A periodic function is a function that repeats a pattern of y- values (outputs) at regular intervals.
Name Period Date LINEAR FUNCTIONS STUDENT PACKET 5: INTRODUCTION TO LINEAR FUNCTIONS
 Name Period Date LF5.1 Slope-Intercept Form Graph lines. Interpret the slope of the graph of a line. Find equations of lines. Use similar triangles to explain why the slope m is the same between any two
Name Period Date LF5.1 Slope-Intercept Form Graph lines. Interpret the slope of the graph of a line. Find equations of lines. Use similar triangles to explain why the slope m is the same between any two
Principles of Mathematics 12: Explained!
 Principles of Mathematics : Eplained! www.math.com PART I MULTIPLICATION & DIVISION IDENTITLES Algebraic proofs of trigonometric identities In this lesson, we will look at various strategies for proving
Principles of Mathematics : Eplained! www.math.com PART I MULTIPLICATION & DIVISION IDENTITLES Algebraic proofs of trigonometric identities In this lesson, we will look at various strategies for proving
13.2 Define General Angles and Use Radian Measure. standard position:
 3.2 Define General Angles and Use Radian Measure standard position: Examples: Draw an angle with the given measure in standard position..) 240 o 2.) 500 o 3.) -50 o Apr 7 9:55 AM coterminal angles: Examples:
3.2 Define General Angles and Use Radian Measure standard position: Examples: Draw an angle with the given measure in standard position..) 240 o 2.) 500 o 3.) -50 o Apr 7 9:55 AM coterminal angles: Examples:
Unit 5. Algebra 2. Name:
 Unit 5 Algebra 2 Name: 12.1 Day 1: Trigonometric Functions in Right Triangles Vocabulary, Main Topics, and Questions Definitions, Diagrams and Examples Theta Opposite Side of an Angle Adjacent Side of
Unit 5 Algebra 2 Name: 12.1 Day 1: Trigonometric Functions in Right Triangles Vocabulary, Main Topics, and Questions Definitions, Diagrams and Examples Theta Opposite Side of an Angle Adjacent Side of
Trigonometric Identities
 Trigonometric Identities Scott N. Walck September 1, 010 1 Prerequisites You should know the cosine and sine of 0, π/6, π/4, π/, and π/. Memorize these if you do not already know them. cos 0 = 1 sin 0
Trigonometric Identities Scott N. Walck September 1, 010 1 Prerequisites You should know the cosine and sine of 0, π/6, π/4, π/, and π/. Memorize these if you do not already know them. cos 0 = 1 sin 0
WESI 205 Workbook. 1 Review. 2 Graphing in 3D
 1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
6.2 Modular Arithmetic
 6.2 Modular Arithmetic Every reader is familiar with arithmetic from the time they are three or four years old. It is the study of numbers and various ways in which we can combine them, such as through
6.2 Modular Arithmetic Every reader is familiar with arithmetic from the time they are three or four years old. It is the study of numbers and various ways in which we can combine them, such as through
* Transversals, Tape, And Stickies! Back to Task Table
 * Transversals, Tape, And Stickies! Back to Task Table Source: Andrew Stadel http://mr-stadel.blogspot.com/2012/10/transversals-tape-andstickies.html In this task, students will reinforce their understanding
* Transversals, Tape, And Stickies! Back to Task Table Source: Andrew Stadel http://mr-stadel.blogspot.com/2012/10/transversals-tape-andstickies.html In this task, students will reinforce their understanding
GREATER CLARK COUNTY SCHOOLS PACING GUIDE. Algebra I MATHEMATICS G R E A T E R C L A R K C O U N T Y S C H O O L S
 GREATER CLARK COUNTY SCHOOLS PACING GUIDE Algebra I MATHEMATICS 2014-2015 G R E A T E R C L A R K C O U N T Y S C H O O L S ANNUAL PACING GUIDE Quarter/Learning Check Days (Approx) Q1/LC1 11 Concept/Skill
GREATER CLARK COUNTY SCHOOLS PACING GUIDE Algebra I MATHEMATICS 2014-2015 G R E A T E R C L A R K C O U N T Y S C H O O L S ANNUAL PACING GUIDE Quarter/Learning Check Days (Approx) Q1/LC1 11 Concept/Skill
Exam: Friday 4 th May How to Revise. What to use to revise:
 National 5 Mathematics Exam Revision Questions Exam: Friday 4 th May 2018 How to Revise Use this booklet for homework Come to after school revision classes Come to the Easter holiday revision class There
National 5 Mathematics Exam Revision Questions Exam: Friday 4 th May 2018 How to Revise Use this booklet for homework Come to after school revision classes Come to the Easter holiday revision class There
