Calculus of Several Variables

Transcription

1 Benjamin McKay Calculus of Several Variables Optimisation and Finance February 18, 2018

2 This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License.

3 Preface The course is divided into two main topics: a. Functions of several variables and their derivatives b. Optimisation (i.e., finding maxima and minima of functions of several variables) It is assumed that you all know how to differentiate standard functions of one variable using the product rule, quotient rule and chain rule for example I fully expect you to be able to find the derivatives of functions such as ( ) x (x 3 +2x 5) 4, x 2 sin 2x, sin 2 x, e 2x+3, e x2, x ln(5x 2 +1), ln, e 2x ln x. 1 + x These notes will make no use of a fixed textbook. If however you wish to consult a supplementary textbook, feel free to look at almost any calculus book in the Library, for example Stewart s Calculus, or see the growing amount of free calculus and economics material on the internet. Several references in the notes will be made to various internet sites that contain relevant material for this course. I do expect you to look at this internet material. These links were working at the time of typing these notes but since the internet is constantly changing if any of the website references are no longer active please let me know and I will pass on this information to the class. You will find plenty of other sites that are helpful for this course search the web for calculus or some particular topic such as elasticity of demand. The only way to learn mathematics is to do exercises. Most sections in these notes end with a collection of Exercises. You will be able to get help with these at the tutorials. iii

4 Contents 1 Functions of several variables 1 2 Partial derivatives 7 3 Partial derivatives in economics 17 4 Optimisation 25 5 Lagrange multipliers 35 List of notation 43 Index 45 iv

5 Chapter 1 Functions of several variables In a previous course, you dealt with functions such as y = f(x), which can also be written as y = y(x): here y, the dependent variable, is a function of a single independent variable x. We graph functions of a single variable in two dimensions using a diagram with x and y-axes like: However as we shall come to see many functions depend on more than one variable. The volume, V, of a cylinder is given by V = πr 2 h. We indicate the dependence of the variable V on the independent variables r and h by writing V = f(r, h) or more commonly V = V (r, h). The temperature, T, on the earth s surface at 12 noon Irish time today depends on where you are, i.e. it is a function of both your latitude x and longitude y; we would write T = f(x, y) or T = T (x, y). The production function is given by Q = f(k, L) or Q = Q(K, L). Here Q is the output of an industry, K is the quantity of capital invested in that industry and L is the quantity of labour used in the industry. The demand function is given by D = f(p, P A, Y ) or D = D(P, P A, Y ) where D is the demand, P is the price of a product, P A is the price of an alternative related product and Y is the income of the customers. For functions of one variable, while any two letters can be used for the dependent and independent variables, very often one works simply with y = f(x). Similarly, for functions of two variables, one frequently uses z = f(x, y). Here x, y are the independent variables while z is the dependent variable; once x and y are specified, then z has no independence and must take a prescribed value. For example, suppose we define z = x 2 + 5y 3 ; if we are then told that x = 3 and y = 1, it must follow that z = (1) 3 = = 14. 1

6 2 Functions of several variables To graph the function z = f(x, y) we need x, y and z-axes: 3 dimensions. Points in 3-dimensional space will have three coordinates (x, y, z). For example the point (0, 1, 0) lies on the y-axis (because the other two coordinates are zero) at the value y = 1. z = 0 is the xy-plane, i.e. all points that lie in the 2-dimensional plane containing the x and y-axes. In two dimensions x = c (constant) is a line perpendicular to the x-axis, y = c is a line perpendicular to the y-axis; in three dimensions x = c is a plane perpendicular to the x-axis, y = c is a plane perpendicular to the y-axis, z = c is a plane perpendicular to the z-axis. z = 2 is the plane consisting of all points at a height of 2 units above the xy-plane. (Here and in the future, think of the xy-plane as being horizontal, and the z-coordinate as giving the height above the xy-plane.) Again it is perpendicular to the z-axis. In fact all planes have an equation of the form c 1 x + c 2 y + c 3 z = c 4, where the c i are constants. The constant c 4 can take any value while some (but not all) of c 1, c 2, c 3 may be equal to zero. For example, the plane z = y: The x-axis lies on this plane because it comprises all points (x, y, z) for which y = 0 and z = 0; and these are points that satisfy the equation z = y and consequently they lie on our plane. An easy-to-use interactive gallery that will aid your understanding of the graphing of planes can be found at in Planes in 3-space under Analytic geometry 2, where you will be able to rotate and zoom the graphs of 5 different planes and be challenged to identify their equations (hint: start with plane number 2, it s the easiest).

7 Functions of several variables 3 What is the graph of y = x? The answer depends on whether we are working in two dimensions (x and y) or three dimensions (x, y and z). In two dimensions the graph of y = x is a straight line, while in three dimensions the graph of y = x is a plane. From the examples we have looked at so far we now know that the graph of a function of one variable, y = f(x), is a curve in 2-dimensional space. The graph of a function of two variables, z = f(x, y), is a surface in 3-dimensional space. A plane is simply a flat surface. In general it is difficult to draw surfaces by hand but there are good computer packages available for this purpose (e.g., Maple, Mathematica, Matlab). The figures that I have plotted here for example have been created using Matlab. A typical surface z = f(x, y): A handy aid to help visualize such surfaces without using a computer is the use of level curves, which are the same as contour lines in geographical maps.

8 4 Functions of several variables A level curve of z = f(x, y) is the set of points (x, y) in the xy-plane that satisfies f(x, y) = k for some constant k. Note here that while the surface z = f(x, y) lies in 3-dimensional space and is usually difficult to draw, each level curve of this surface lies in the standard xy-plane and so is often easy to draw. Consider the surface z = x 2 + y 2. Its level curves are the points (x, y) such that x 2 + y 2 = k. Now for k > 0 this is simply a circle with centre (0, 0) and of radius k. Level curves: Try to visualize the surface z = f(x, y) by lifting each level curve to its corresponding height k: Consider the surface z = x 2 + 2y 2. Its level curves are the points (x, y) such that x 2 + 2y 2 = k. For each k > 0 the level curves in this case is given by an ellipse: The actual surface z = x 2 + 2y 2 is obtained by lifting each level curve to its height k:

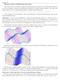
9 Functions of several variables 5 Finally, to take a complicated example, consider the level curves: What does the corresponding surface look like? In fact this is the surface we saw on page 3 (a few of the level curves were already drawn in that figure). Inside each closed level curve, there is a maximum or a minimum. Where two level curves cross there is neither a maximum nor a minimum, but a saddle point. Exercises a. In three dimensions, sketch the graphs of the functions (a) z = 3 (b) z = 3 (c) x = 1 (d) y = 1 (e) y = x (f) y = 2x (g) z = x. b. By first plotting the points where each plane intersects the coordinate axes, sketch in three dimensions the graphs of the functions (a) z = 1 x y (b) z = 2 x + y (c) x + y = 3 c. Plot some level curves of the surface z = x 2 + y 2. Hence sketch the surface. Can you see how it differs from the surface z = x 2 + y 2 of Example 1? Hint: what does the function of one variable graph y = x 2 look like?

10

11 Chapter 2 Partial derivatives Definition Even without graphing the function z = f(x, y), one can still deduce extremely important properties of the surface by making use of calculus. If you recall from your earlier courses and leaving certificate mathematics courses there is a lot of information that we can deduce from a function by using calculus, for example, calculating the slope, points of inflection, whether the graph is increasing or decreasing, etc. In this course we again follow similar trains of exploration however in our case we have more than one variable. We begin this study in this section. Given a function z = f(x, y), the partial derivative of f with respect to x, written f x or f x, is obtained by differentiating f(x, y) with respect to x while treating y as a constant. Similarly, f y or f y is obtained by differentiating f(x, y) with respect to y while treating x as a constant. Take the function z = f(x, y) = x 3 + x 2 y 3 2y 2 + e xy. Find f x (2, 1) and f (2, 1). y In order to do this, you must first calculate and then plug in (x, y) = (2, 1). f x (x, y) = 3x 2 + 2xy 3 + ye xy, f y (x, y) = 3x 2 y 2 4y + xe xy 7

12 8 Partial derivatives Geometric interpretation of partial derivatives For y = f(x), the derivative dy/dx is the slope of the tangent line to the curve y = f(x). For z = f(x, y), the partial derivative f x is the slope of the tangent line to the surface z = f(x, y) in the x-direction. We see f x at the point (x 0, y 0 ): In computing f x one keeps y constant, so in the diagram all the action takes place in the plane y = y 0, which is perpendicular to the y-axis (i.e., parallel to the xz-plane). The intersection of this plane with the surface z = f(x, y) is a curve (see the figure). Technically this curve is defined by z = f(x, y 0 ), i.e., along the curve z is a function of a single variable x. Thus we find the slope of the tangent to this curve in the standard 1-dimensional way, by differentiating with respect to x. That is, f x (x 0, y 0 ) is the slope of the line tangent to the curve. In this diagram the line is falling as x increases (i.e., as x moves from right to left) so the slope of the line is negative. That is, f x (x 0, y 0 ) < 0. Similarly, f y (x 0, y 0 ) gives the slope of the line that is tangent to the curve where the surface z = f(x, y) intersects the plane x = x 0 : In this diagram the line appears to be horizontal as y increases (i.e., as y moves from left to right) so the slope of the line is zero. That is, f y (x 0, y 0 ) = 0. At the webpage rogness/multivar/partialderivs.shtml

13 Geometric interpretation of partial derivatives 9 you ll find a nice interactive discussion of the geometric interpretation of partial derivatives: at a point on a surface, two lines are drawn whose slopes are the partial derivatives with respect to x and y. With the mouse you can drag this point around on the surface and see how this changes the slopes of the two lines (i.e., the values of the partial derivatives). Can you predict what positions the lines will take when you drag the point to the flat part of the surface? Analogously to functions of one variable, one can also interpret partial derivatives as rates of change: f x is the rate of change of f with respect to x when y is fixed, and f y is the rate of change of f with respect to y when x is fixed. Recall that for the function of one variable y = log e x = ln x (where x > 0), one has dy/dx = 1/x. Hence for example we have Take the function d(ln 2x) dx = 1 2x d(2x) dx = 1 2x 2 = 1 x. ( ) x z = f(x, y) = ln. 1 + y Let s find f x and f y. We could differentiate this immediately using the chain rule for functions of one variable followed by the quotient rule: ( ) z x = x = 1 + y (1 + y)(1) (x)(0) x 1 + y x (1 + y) 2 = 1 + y 1 + y x (1 + y) 2 = 1 x, 1 x 1+y but it s easier to apply first a standard property of the ln function before differentiating: ( ) x z = ln = ln x ln(1 + y) 1 + y so z x = 1 x 0 = 1 x because 1 + y is a constant when we are differentiating with respect to x. Similarly, differentiating z = ln x ln(1 + y) yields z y = (1) = 1 + y 1 + y. For functions of three or more variables, partial derivatives are computed with respect to an independent variable by holding all other variables constant. Exercises a. f(x, y, z) = e xy ln z, find f x, f y and f z by using the chain rule. b. f(x, y) = x 3 y 5, find f x (3, 1). Ans: 27 c. f(x, y) = xe y + 3y, find f y (1, 0). Ans: 2

14 10 Partial derivatives d. z = sin(y x), find z x (3, 3) e. z = x3 + y 3 x 2 + y 2, find z y Ans: Ans: 1 3x 2 y 2 2x 3 y + y 4 (x 2 + y 2 ) 2 f. z = x y y x, find z x Ans: y + y g. z = ln(x 2 + y 2 ), find z x Ans: 2 x 3 2x x 2 + y 2 h. z = 25 x 2 y 2, find z x x 25 x2 y, 2 y 25 x2 y 2 and z y Ans: i. The temperature at a point (x, y) is given by T (x, y) = 60/(1 + x 2 + y 2 ). Find the rate of change of temperature with respect to distance at the point (2,1) in (a) the x-direction (b) the y-direction. Ans: (a) 20/3 (b) 10/3. The tangent plane Recall that for y = f(x), the slope of the tangent line is f (x) and this information enables one to compute the equation of the tangent line: y y 0 = f (x 0 ) (x x 0 ). Correspondingly, for any surface z = f(x, y), at each point one has a unique tangent plane. The tangent plane is the plane that passes through both tangent lines. Equivalently, it is the plane that just touches the surface z = f(x, y) at the point (x 0, y 0, z 0 ), where z 0 = f(x 0, y 0 ). See the tangent plane to the surface z = 3 + x y2 9 at the point (x 0, y 0 ) = ( 4, 3): Given z = f(x, y) and a point (x 0, y 0 ), we can compute z 0 = f(x 0, y 0 ), z x (x 0, y 0 ) and z y (x 0, y 0 ). The equation of the tangent plane to z = f(x, y) at the point (x 0, y 0, z 0 ) is ( ) ( ) z z z z 0 = x (x 0, y 0 ) (x x 0 ) + y (x 0, y 0 ) (y y 0 ).

15 Differentials 11 Know this formula. z Observe here that z 0, x (x 0, y 0 ) and z y (x 0, y 0 ) are numbers; the only variables in this formula are z on the left-hand side and x, y on the right-hand side. Exercises a. Find the equation of the tangent plane to the surface z = 2x 2 + y 2 at the point x = 1, y = 1. b. Find the equation of the tangent plane to the given surface at the specified point: 1. z = x 2 + 4y 2, (2, 1, 8) Ans: 4x + 8y z = 8 2. z = 5 + (x 1) 2 + (y + 2) 2, (2, 0, 10) Ans: 2x + 4y z + 6 = 0 3. z = ln(2x + y), ( 1, 3, 0) Ans: 2x + y z = 1 4. w = xy + 3y 2, ( 2, 3, 21) Ans: w = 3x + 16y z = cos(x y), (π/2, 0, 0) Ans: x y + z = π/2 6. z = y cos(x y), (2, 2, 2) Ans: z = y 7. z = 4 x 2 2y 2, (1, 1, 1) Ans: x 2y + z = 4 c. (MS3003 Autumn 2008 exam) Find the equation of the tangent plane to the surface z = 4x 2 y 2 + 2y at the point ( 1, 2, 4). Ans: z = 8x 2y Differentials Let s start with the function of one variable y = f(x). The derivative of this function is f f(x + x) f(x) (x) = lim. x 0 x The definition of limit means that when x is close to zero, we have f (x) f(x + x) f(x) x Rearranging this approximate equation, one gets f(x + x) f(x) + f (x) x. (2.1) Thus if we know the values of f(x) and f (x), then using (2.1) we can easily compute the approximate value of f at the nearby point x + x. Let s use (2.1) and 9 = 3 to approximate 10. Here the key fact is that 9 = 3, i.e., for the function f(x) = x and x = 9 we have f(9) = 3. Now. f (x) = 1 2 x 1/2

16 12 Partial derivatives so f (9) = = = 1 6. We want 10 = f(10). Hence x + x = 10, i.e., x = 1 because from above x = 9. From (2.1) we now get 10 = f(10) f(9) + f (9) (1) = (1) = 31 6 = A calculator will give 10 = (to 4 decimal places) so our approximation was fairly good. Equation (2.1) computes (approximately) the change in the dependent variable y = f(x) when the independent variable x changes by x. This change in y is written y, so y = f(x + x) f(x), and (2.1) then becomes y = f(x + x) f(x) f (x) x. This gives (approximately) the change y in y as a result of a small change x in x. The quantities x and y are called differentials. Consider now a function of two variables z = f(x, y). We want to compute (approximately) the change z in the dependent variable z when the independent variable x changes by x and the independent variable y changes by y; here x and y are both small. Recall that z x is computed using the rules for differentiating a function of one variable, with y held constant. Thus it follows from our discussion of functions of one variable above that a change x in x will induce (approximately) a change z x x in z. Similarly, a change y in y will induce (approximately) a change z y y in z. Consequently the total change in z that will be caused by a small change x in x and a small change y in y is z z z x + y. (2.2) x y This approximation by differentials of the change in a dependent variable is used frequently in various applications to Economics that we shall discuss later in this module. When we are asked to estimate the change in..., then usually we shall use (2.2) or some variant of it. Exercises a. Let z = x 3 y y 3 x. Use differentials to find approximately the total change in z when x increases from 1 to 1.1 and simultaneously y decreases from 3 to 2.8.

17 The chain rule 13 When differentials are used to compute approximately the change in z induced by changes in x and y, we are in fact approximating the surface z = f(x, y) by its tangent plane at the point (x, y) and computing the exact change in z on this tangent plane that is induced by the changes in x and y. This approximates the change in the surface z = f(x, y) because near the point (x, y) the tangent plane is a good approximation of the surface. Exercises a. Let z = 7x 4 y 2x 4 y 2. Find the first-order partial derivatives of z and evaluate these derivatives when x = 4 and y = 2. Hence estimate the change in z that is associated with an increase in x to and a decrease in y to Ans: At x = 4, y = 2, get z x = 1536, z y = 256, z b. Given the sales function S = ( P )A 2/3 r 1/4 where P is price, A is spending on advertising, and r is the number of sales representatives, use differentials to estimate the change in sales from 1. hiring an extra sales representative 2. a e1 increase in advertising 3. a e0.01 reduction in price when P = 4, A = e6000 and r = 24. Ans: 83742, , The chain rule For functions of a single variable, the chain rule is: if y = f(x) and x = g(t), then y = f(g(t)) and dy dt = dy dx dx dt. For functions of more than one variable, the chain rule can take various forms, as we shall see in the examples that follow. The idea is to sum up over all possible dependencies of variables on one another. Exercises a. Suppose that z = f(x, y), where x = g(t) and y = h(t). Thus z = f ( g(t), h(t) ), i.e., z depends on t. Express dz z dt in terms of x, z y, dg dt and dy dt. (Recall that the -notation is used for functions of two or more variables while the d-notation is used only for functions of one variable.) Use your formula to find dz dt if z = x2 y + 3xy 4, x = e t and y = sin t. The chain rule formula for dz dt : take the product of derivatives along each possible chain of variable dependencies from z to t, then add these products: dz dt = f dx x dt + f dy y dt.

18 14 Partial derivatives Exercises a. Suppose that z = e x sin y, where x = st 2 and y = s 2 t. (Thus z depends ultimately on s and t.) Find z s. b. Suppose that u = x 4 y + y 2 z 3, where x = rs, y = s 2 and z = r 2 s sin t. when r = 2, s = 1 and t = 0. Find u s and u t c. z = x 2 + y 2, x = t 3, y = 1 + t 2, find dz dt. Ans: 6t5 + 4t 3 + 4t. d. z = ln(x + y 2 ), x = 1 + t, y = 1 + t, find dz Ans: dt. 1 x + y 2 ( t + y ). t e. w = xy 2 z 3, x = sin t, y = cos t, z = 1 + e 2t, find dw dt. Ans: y 2 z 3 cos t 2xyz 3 sin t + 6xy 2 z 2 e 2t. f. z = x 2 sin y, x = s 2 + t 2, y = 2st, find z s and z t. Ans: 4sx sin y + 2tx 2 cos y, 4tx sin y + 2sx 2 cos y. g. If z = x 2 + xy, x = st + t 2 and y = t 3 1, use the chain rule to find z s when s = 2 and t = 1. and z t h. The radius of a cylinder is decreasing at a rate of 1.2 cm/sec while its height is increasing at a rate of 3 cm/sec. At what rate is the volume of the cylinder changing when the radius is 80 cm and the height is 150 cm? Ans: 9600π cm 3 /sec. i. Sand is pouring onto a conical pile in such a way that at a certain instant the height is 100 cm and increasing at 3 cm per minute while the base radius is 40 cm and increasing at 2 cm per minute. How fast is the volume increasing at that instant? Ans: (20800π/3) cm 3 /min j. The pressure P (in kilopascals, i.e. kpa), volume V (in litres) and temperature T (in degrees kelvin) of a gas are related by the equation P V = 8.31T. Find the rate at which the pressure is changing when the temperature is 300 K and increasing at a rate of 0.1 K/sec and the volume is 100 L and increasing at a rate of 0.2 L/sec. Ans: kp a/sec k. Wheat production W in a given year depends on the average temperature T and the annual rainfall R. It is estimated that the average temperature is rising at a rate of 0.15 C per year and rainfall is decreasing at a rate of 0.1 cm per year. They also estimate that at current production levels W T W = 2 and R = What is the significance of the signs of these partial derivatives? 2. Estimate the current rate of change of wheat production dw dt. Ans: decreasing at 1.1 units/year

19 Higher-order derivatives 15 l. (MS3003 Autumn 2008 exam) If z = f(x, y) where x = s+t and y = s t, show that ( ) 2 ( ) 2 z z = z z x y s t. m. Suppose z = f(x, y) with x = r cos θ, y = r sin θ. Find z r show that ( ) 2 ( ) 2 ( ) 2 z z z + = + 1 ( ) 2 z x y r r 2. θ Higher-order derivatives For y = f(x), recall that d 2 y dx 2 means d dy dx dx ; z and θ and it can also be written as (f ) (x), i.e., f (x). Similarly, given z = f(x, y), if we first compute f x, then we can differentiate this new function: f x x = 2 f x 2 = (f x) x = f xx, f y x = 2 f y x = (f x) y = f xy. Note that 2 f y x and f xy have the same meaning even though x and y appear in different orders! Similarly, f y y = 2 f y 2 = (f y) y = f yy, f x y = 2 f x y = (f y) x = f yx. Exercises a. Find all second-order partial derivatives of z = x 3 + x 2 y 3 2y 2. In this example it turns out that z xy = z yx. This is usually true; only for certain exceptional functions is it false. (In this module it will be true for all functions that we meet.) b. Verify that z = e 4y sin x satisfies the equation z y 4 2 z x 2 = 0. c. Find all second-order partial derivatives if (i) z = x 2 y + x y Ans: z xx = 2y, z xy = 2x y, z yy = x 4 y 3

20 16 Partial derivatives (ii) z = (x 2 + y 2 ) 3/2 3xy Ans: z xy = (x 2 + y 2 ), z 1/2 xx = 3(x 2 + y 2 ) 1/2 3x 2 + (x 2 + y 2 ), 1/2 z yy = 3(x 2 + y 2 ) 1/2 3y 2 + (x 2 + y 2 ) 1/2 d. (Autumn 2008 MS3003 exam) Find all first-order and second-order partial derivatives of z = sin(xy). Ans: z x = y cos xy, z y = x cos xy, z xy = cos xy xy sin xy, z yy = x 2 sin xy, z xx = y 2 sin xy e. (Spring 2011 MA3301 exam) Find all the first-order and second-order derivatives of the function f(x, y) = xe xy + 11y. Ans: f x = (1 + xy)e xy, f y = x 2 e xy, f xx = (2y + xy 2 )e xy, f xy = (2x + x 2 y)e xy, f yy = x 3 e xy. f. Verify that 2 z y x = 2 z x y if (i) z = x y + ln(xy) (ii) z = sin(2 + x 2 y) g. Verify that z = (x 2 + y 2 ) 1/2 satisfies the equation 2 z x z y 2 = (x2 + y 2 ) 3/2. h. Verify that z = ln(x 2 + y 2 ) and z = e x cos y e y cos x both satisfy the equation z xx + z yy = 0.

21 Chapter 3 Partial derivatives in economics In this chapter we shall examine elasticity, production and utility. Elasticity Suppose that the demand Q for a good depends on its price P, the price P A of an alternative good and the income Y of customers, i.e., Q = Q (P, P A, Y ). First consider how the demand Q varies when P changes while P A and Y do not vary [think... this is something to do with Q P ]. Two initial observations: a. As P increases we expect Q to decrease, so we assume that Q P < 0. b. The effect of an increase in P by say 1 unit depends on the size of P ; e.g., increasing the price of a car by e 1 has no effect on demand but increasing the price of a bar of chocolate by e 1 has a large effect. Thus instead of considering the change P in P we consider the percentage change in P, viz., 100 P P. Similarly it makes sense to consider the percentage change in Q. The own price elasticity of demand is percentage change in Q E P = 100 Q Q Q Q percentage change in P = P P = Q P P Q Q P P Q. One typically has E P > 0 (this is why the minus sign is included in the formula). It is a measure of how sensitive in percentage terms the quantity demanded is to changes in the price of the good. Similarly, the income elasticity of demand is E Y = Q Y Y Q. When E Y > 0, i.e., increasing income Y increases demand Q so Q Y > 0, we say the good is superior. But E Y < 0 means that the good is inferior, i.e., 17

22 18 Partial derivatives in economics increased income Y leads consumers to switch to a better-quality alternative good. Similarly, the cross-price elasticity of demand is E PA = Q P A P A Q. If E PA > 0 then we say that P A is a substitute good: when the price P A of the alternative good goes up, demand for our good increases. For example, consumers might switch from one brand of coffee to another when prices of the first brand go up. If E PA < 0 then we say that P A is a complementary good: when the price P A goes up, demand for our good decreases. For example, suppose our good is DVDs and P A is the price of DVD players; if P A increases then fewer DVD players will be sold, which means that fewer people will buy our DVDs, i.e., demand for our good decreases. Exercises a. Given the demand function Q = 100 2P + P A + 0.1Y, find the partial elasticities of demand at P = 10, P A = 12 and Y = Elasticity in terms of the ln function A straightforward partial derivative shows how one quantity depends on another: if z = f(x, y), then z x measures how z changes as x varies (with y held fixed). But if we want to see the percentage change in z expressed in terms of the percentage change in x, then (recall the derivation of E P ) this is given by the elasticity z x ln z, which is often written as x z ln x, the elasticity of z with respect to x, or the x-elasticity of z. Exercises a. Given the demand function Q = 150 5P P Y, where P 1 = 5, P 2 = 10 and Y = 800, calculate the own price elasticity of demand, cross-price elasticity of demand, and the income elasticity of demand. Is the good inferior or superior? Is the alternative good substitutable or complementary? Ans: 0.057, 0.34, 0.37, superior, substitutable. b. Given the demand function Q = 500 3P 2P A Y, when P = 20, P a = 30 and Y = 5000 find the own price elasticity of demand, crossprice elasticity of demand, and the income elasticity of demand. If income rises by 5%, calculate the corresponding percentage change in demand. Is the good inferior or superior? Is the alternative good substitutable or complementary?

23 Partial derivatives in economics 19 Ans: (to 4 decimal places) E P = , E PA = , E Y = , % change , superior, complementary. c. The demand functions for products A and B are functions of their prices given by Q A = 50 3 P B and Q B = 75P A. PA P 2 B 3 Find the four price elasticities and determine whether the products are complementary or substitutable. Q Ans: A P A = 25P 3/2 A P 1/3 B, Q A P B = 50 3 P 1/2 A P 2/3 B, Q B P A = 75P 2/3 Q B, B P B = 50P A P 5/3 B, substitutable. d. Use the ln function formulation of elasticity to show the following: if z = f(x, y), then the elasticity of z with respect to x is constant for all x if and only if z = g(y)x k for some constant k and some function g(y) with g(y) > 0. Note: this short theoretical exercise relies on standard properties of the ln and exponential functions. Production Assume that output Q depends on capital K and labour L, so Q = Q(K, L). Then we define marginal product of capital: MP K.= Q K marginal product of labour: MP L.= Q L. The level curves of Q are called isoquants. These are curves in the (K, L) plane along each of which Q is constant.

24 20 Partial derivatives in economics Here the L axis is horizontal, the K axis is vertical, and isoquants are drawn for Q = 100, 150 and 200. Three isoquants are drawn for the production function Q = KL. The shapes of these curves are typical of many isoquants: as capital K is reduced on any of the curves, in order to maintain production at the same level Q (i.e., to remain on the isoquant) one must increase the labour component L. Looking at this more closely, we observe that as K gets small, a small decrease in K requires a large increase in L in order to stay on the isoquant. This trade-off between capital and labour is quantified by the marginal rate of technical substitution, which we shall define in a moment. Consider a particular isoquant. On it one has K = K(L), e.g., the lowest isoquant is 100 = Q = KL which gives K = 100/L on that isoquant. Thus it makes sense to write dk/dl for the slope of our isoquant. The marginal rate of technical substitution on this isoquant is MRTS.= dk dl, (3.1) which measures the slope of the isoquant (the minus sign is present to ensure that MRTS > 0 as the isoquant is a decreasing function so its slope is negative). We now derive a more practical formula for MRTS. As we just saw, when moving along an isoquant one has K = K(L). Hence along the isoquant dq dl = Q dk K dl + Q L. But Q is constant along the isoquant so dq/dl = 0, i.e., 0 = Q dk K dl + Q L

25 Partial derivatives in economics 21 which is easily rearranged to get MRTS = dk dl = Q L Q K = MP L MP K, (3.2) where Q L.= Q L and Q K. = Q K, i.e., along each isoquant the marginal rate of technical substitution equals the marginal product of labour divided by the marginal product of capital. Exercises a. Evaluate MP K and MP L for the production function Q = 2LK + L, given that the current values of K and L are 7 and 4 respectively. Hence (a) Compute the value of MRTS. (b) Use the value of MRTS to estimate the increase in capital needed to maintain the current level of output if there is a 1-unit decrease in labour. We find an expression for MRTS for the Cobb Douglas production function Q = AK α L β where A, α and β are positive constants. Taking partial derivatives, we have Thus MP K = Q K = αakα 1 L β and MP L = Q L = βakα L β 1. MRTS = MP L MP K = βakα L β 1 αak α 1 L β = βk αl. In production, the following question is of particular interest: what is the effect on output if all inputs are scaled in the same way? For example, if we double capital and double labour, what happens to output? Consider the Cobb Douglas production function Q(K, L) = AK α L β and suppose that capital and labour are scaled by a factor λ > 0, i.e., K is replaced by λk and L is replaced by λl. Then the output becomes Q(λK, λl) = A(λK) α (λl) β = AK α L β λ α+β = λ α+β Q(K, L). (3.3) Any function f(k, L) is said to be homogeneous of degree n if f(λk, λl) = λ n f(k, L). Thus (3.3) shows that Cobb-Douglas production is homogenous of degree α + β. If (i) α + β = 1 we have constant returns to scale, (ii) α + β > 1 we have increasing returns to scale, (iii) α + β < 1 we have decreasing returns to scale.

26 22 Partial derivatives in economics Exercises a. (MA3301 Spring 2010 exam) The production function of a company is given by Q(K, L) = 3K 2 + 7L, where Q is the number of units produced, K is the amount of capital needed and L is the number of labour hours used. Suppose that K = 250 and L = Determine the values of the marginal products of capital and labour. 2. Estimate the change in output if K increases by 1 unit. 3. Estimate the increase in K required to maintain current output levels if L decreases by 5 units. Ans: b. (MA3301 Spring 2011 exam) The production function of a company is given by Y (K, L) = 10K 0.4 L 0.3, where Y is the number of units produced, K is the amount of capital used and L is the number of labour hours used. Let K = 100 and L = Determine the marginal products of capital and labour. 2. Estimate the change in output when K increases by 1 unit and L decreases by 2 units. 3. Determine the elasticity of production with respect to capital and labour. 4. Estimate the % change in output when K increases by 5% and L decreases by 10%. Ans: c. Given the production function Q = K 2 + 2L 2, write down expressions for the marginal products of capital and labour. Hence show that MRTS = 2L K and K Q K + L Q L = 2Q. Utility To analyse quantitatively the behaviour of customers, we associate with each set of options a number U, the utility that indicates the level of satisfaction. Suppose that there are two goods G 1 and G 2 and the consumer buys x 1 and x 2 units respectively of these two goods. Then U is a function of x 1 and x 2, i.e., U = U (x 1, x 2 ). The marginal utility of the good G i is defined to be U x i, for i = 1, 2.

27 Partial derivatives in economics 23 If x 1 changes by a small amount x 1, then the change in U is U U x 1 x 1 and similarly for x 2. If both x 1 and x 2 change, then U U x 1 x 1 + U x 2 x 2. This equation is just (2.2) written in different notation. Exercises a. Suppose that a utility function is given by U(x 1, x 2 ) = x 1/2 1 x 3/4 2. Determine the marginal utilities when x 1 = 100 and x 2 = 200. Hence estimate the change in U when x 1 decreases from 100 to 99 and x 2 increases from 200 to 201. In this example, one can show [exercise!] that 2 U x 2 1 = 3 16 x 7/4 1 x 3/4 2 and 2 U x 2 2 = 3 16 x1/4 1 x 5/4 2. These are both negative. Now 2 U x 2 1 < 0 implies that the marginal utility U x 1 is a decreasing function. That is, as the consumption of the good G 1 increases, each additional item of G 1 that is bought confers less utility than the previous item. Similarly for G 2. This property, which holds true for many utility functions, is known as the law of diminishing marginal utility. The level curves of U are called indifference curves. These are curves in the (x 1, x 2 ) plane along each of which U is constant. This is exactly the same mathematical situation as the isoquants of Section 3; only the English terminology is different. Thus the graphs in of isoquants could be considered indifference curves, with the x 1 axis horizontal and the x 2 axis vertical. The marginal rate of commodity substitution on any particular indifference curve is defined to be MRCS.= dx 2 dx 1 on that indifference curve. This is the same as (3.1); only the letters used are different. Hence one can show, in exactly the same way as (3.2) was derived, that where U x1.= U x 1 and U x2.= U x 2. MRCS = U x 1 U x2 (3.4)

28 24 Partial derivatives in economics Exercises a. Given the utility function U(x 1, x 2 ) = x 1/2 1 x 1/2 2, find a general formula for MRCS in terms of x 1 and x 2. Calculate the particular value of MRCS for the indifference curve that passes through the point (300, 500). Hence estimate the increase in x 2 needed to maintain the current level of U when x 1 decreases by 3 units. b. Prove the formula (3.4) by imitating the derivation of (3.2). c. Given the utility function U (x 1, x 2 ) = x 1/2 1 x 1/3 2, determine the value of the marginal utilities when x 1 = 25 and x 2 = 8. Hence estimate the change in utility when x 1 and x 2 both increase by one unit, and find the marginal rate of commodity substitution at this point. Ans: 0.2, ; , 0.48 d. An individual s utility function is U (x 1, x 2 ) = 1000x x 2 + 5x 1 x 2 2x 2 1 x 2 2, where x 1 is the amount of leisure measured in hours per week and x 2 is earned income measured in Euro per week. Determine the value of the marginal utilities when x 1 = 138 and x 2 = 500. Hence estimate the change in U if the individual works for an extra hour which increases earned income by 15 Euro per week. Does the law of diminishing marginal utility hold for this function U? Calculate the value of the marginal rate of commodity substitution when x 1 = 138 and x 2 = 500. Hence estimate the increase in earned income required to maintain the current level of utility if leisure falls by two hours per week. Ans: 2948, 140; 848, yes, , e. (MA3301 Spring 2011 exam) An individual s utility function is given by U (x 1, x 2 ) = x x 2 2 x 1 x 2, where x 1 is the number of cups of tea drunk per week and x 2 is the number of bottles of beer drunk per week. Let x 1 = 30 and x 2 = Find the marginal utilities with respect to tea and beer. 2. Estimate the change in utility if x 1 increases by 4 items per week and x 2 decreases by 1 item per week. 3. Derive the formula for the elasticity of substitution R x2x 1 [This is another name for the MRCS described above in the Notes; the exam question is asking you to derive equation (3.4)] 4. Estimate the increase in tea drinking required to maintain the same level of utility if beer drinking were reduced by 1 bottle per week. Ans: (a) 56, 50, (b) 174, (d) 25/28.

29 Chapter 4 Optimisation Maximum and minimum values for functions of two variables In this section we show to use partial derivatives to examine a function z = f(x, y) in order to determine the locations of maxima and minima (if there are any) of z. A search for such points is often called optimisation of z. A global maximum of f(x, y) is a point (x 0, y 0 ) so that f (x 0, y 0 ) f (x, y) for all points (x, y) for which f(x, y) is defined. A local maximum of f(x, y) is a point (x 0, y 0 ) so that f (x 0, y 0 ) f(x, y) for all points (x, y) near enough to (x 0, y 0 ) at which f(x, y) is defined. A global minimum of f(x, y) is a point (x 0, y 0 ) so that f (x 0, y 0 ) f (x, y) for all points (x, y) for which f(x, y) is defined. A local minimum of f(x, y) is a point (x 0, y 0 ) so that f (x 0, y 0 ) f(x, y) for all points (x, y) near enough to (x 0, y 0 ) at which f(x, y) is defined. From the graph of the surface (or from the level curves, if they were labelled) we can see that this function has three local maxima, one of which is the only absolute maximum, and two local minima. An extremum is a maximum or minimum. To help find local extrema we use the following theorem, which is analogous to the corresponding result for functions of one variable. A point (x 0, y 0 ) where f (x 0, y 0 ) is defined is a critical point of f if a. the point (x 0, y 0 ) lies on the boundary of the points (x, y) where f(x, y) is defined or b. the partial derivatives f x and f y don t exist at (x, y) = (x 0, y 0 ) or c. 0 = f x = f y at (x 0, y 0 ). 25

30 26 Optimisation Theorem 4.1. Local extrema of any function f(x, y), if they occur at all, can only occur at critical points. Theorem 4.1 says that to find extrema, one need consider only critical points. As we shall see, a critical point might not be an extremum, or even a local extremum, so after finding the critical points we then need to test each one to determine if it gives a local extremum. (This is analogous to functions of one variable, where putting dy/dx = 0 can give an extremum or a point of inflection.) Exercises a. Find all extrema of the function b. Find all extrema of the function f(x, y) = x 2 + y 2 2x 6y f(x, y) = y 2 x 2. A function g(x, y) is continuous in a region of the (x, y)-plane if its graph z = g(x, y) has no gaps or tears there. (In practice, although we ll mention this condition in the next theorem, we won t verify if it holds true, since all functions appearing in these Notes are continuous.) The ad hoc approach used to analyse critical points in our previous examples cannot be used in most examples. Instead we shall use the following result, which is an analogue of the related test used for functions of one variable. Know the next theorem precisely. Theorem 4.2. [Second Derivative Test for critical points] Take a critical point (x 0, y 0 ) of a function f(x, y). Assume that f xx, f yy and f xy are continuous near (x 0, y 0 ). Set = ( f xx f yy f 2 xy) (x,y)=(x0,y 0). a. If > 0 and f xx (x 0, y 0 ) > 0, then f has a local minimum at (x 0, y 0 ). b. If > 0 and f xx (x 0, y 0 ) < 0, then f has a local maximum at (x 0, y 0 ). c. If < 0, then f has a saddle point at (x 0, y 0 ). d. If = 0, then the test gives no information.

31 Applications to economics 27 Exercises a. Find the local extrema of the function f(x, y) = x 4 + y 4 4xy + 1. b. Find the local extrema and saddle points of f. 1. f(x, y) = x 2 + y 2 + 4x 6y. Ans: minimum at ( 2, 3, 13). 2. f(x, y) = 2x 2 + y 2 + 2xy + 2x + 2y. Ans: minimum at (0, 1, 1). 3. f(x, y) = 6x 2 9x 3xy 7y + 5y 2. Ans: minimum at (1, 1, 8). 4. f(x, y) = x 2 + y 2 + x 2 y + 4. Ans: minimum at (0, 0, 4), saddle points at (± 2, 1, 5). 5. f(x, y) = x 3 3x + xy 2. Ans: minimum at (1, 0, 2), maximum at ( 1, 0, 2), saddle points at (0, ± 3, 0). 6. f(x, y) = x2 y 2 8x + y, where x 0 and y 0. Ans: max at xy ( 1 2, 4, 6). 7. f(x, y) = e x cos y. Ans: none. 8. (MS3003 Autumn 2008 examination) f(x, y) = x + y + x 2 y + xy 2 Ans: saddle points at (1, 1, 0) and ( 1, 1, 0) c. (MA3301 Autumn 2011 examination) Find and classify the stationary points of f(x, y) = x 3 + y 3 6xy. [Note: stationary point is another name for critical point ] Ans: saddle point at (0, 0), minimum at (2, 2). d. Let w = f(x, y) be a function of two variables. Give a detailed statement of a test that can determine the nature of the critical points of f. Use this test to examine the critical points of the function f(x, y) = x 3 + 2y 3 3x 2 24y Ans: minimum at (2, 2, 20), maximum at (0, 2, 48), saddle points at (0, 2, 16) and (2, 2, 44). Applications to economics Exercises a. A producer sells two goods G 1 and G 2 at e1,000 and e800 each respectively. The total cost of producing the goods is given by T C = 2Q Q 1 Q 2 + Q 2 2 where Q 1 and Q 2 denote the output levels of G 1 and G 2. Find the maximum possible profit and the values of Q 1 and Q 2 at which this is achieved.

32 28 Optimisation b. A firm is allowed to charge different prices to its domestic and industrial customers. If P 1 and Q 1 denote the price and demand for the domestic market then the demand equation is P 1 + Q 1 = 500. If P 2 and Q 2 denote the price and demand for the industrial market then the demand equation is 2P 2 + 3Q 2 = 720. The total cost of production is T C = 50, (Q 1 + Q 2 ). Determine the pricing policy for the firm that will optimise profit with price discrimination and calculate the value of the maximum profit. c. A firm is a monopolistic producer of two goods G 1 and G 2. Their prices P 1 and P 2 are related to the quantities Q 1 and Q 2 produced by the demand equations P 1 = 50 Q 1, P 2 = 95 3Q 2. If the total cost of producing Q 1 and Q 2 is T C = Q Q 1 Q 2 + Q 2 2, show that the firm s profit function is π = 50Q 1 2Q Q 2 4Q 2 2 3Q 1 Q 2. Hence find the values of Q 1 and Q 2 that maximize the profit of the firm and deduce the corresponding prices of G 1 and G 2. Ans: Q 1 = 5, Q 2 = 10, max profit = 600, P 1 = 45, P 2 = 65. d. A firm has the possibility of charging different prices P 1 and P 2 in its domestic and foreign markets. The corresponding demand equations are given by Q 1 = 300 P 1, Q 2 = 400 2P 2. The total cost function is T C = Q, where Q = Q 1 + Q 2. Determine the prices that the firm should charge to optimise its profit with price discrimination and calculate the value of this maximum profit. Ans: P 1 = 200, P 2 = 150, maximum profit = 10,000. e. (MA3301 Spring 2011 examination) A business sells two products. Product 1 sells for x Euro per item and the business sells x units of it. The business can sell y units of Product 2 for y Euro per item. What should be the prices of the two products to maximize revenue? Ans: x = 1000, y = f. (MA3301 Spring 2011 examination) A hotel charges different prices for the same meal in two different markets. The demand function in each market is given by p 1 = 50 4q 1 and p 2 = 80 3q 2, where p 1, p 2 are the prices of the meal and q 1, q 2 are the quantities demanded in each market. The company s total cost T C is given by T C = (q 1 + q 2 ). Find 1. the total sales revenue T R; 2. the total profit T P ; 3. the optimal prices that should be charged for the meal in each market to maximize total profit.

33 Constrained optimisation by substitution 29 Constrained optimisation by substitution In this section we again consider how to find maxima and minima of a function z = f(x, y), but now with the extra requirement that x and y are related in some way by a constraint such as x 2 + y 2 = 3. There are two standard techniques for such problems: a. Make an algebraic substitution to remove one of the variables. This approach cannot always be used because it is sometimes impossible to sort out the algebra to make the substitution. b. Use Lagrange multipliers to handle the constraint. In principle this technique can always be used, but later in the problem one may run into difficulties in solving the equations to find the critical points. We shall examine this approach later in the course. Let s find the minimum value of the objective function z = 2x 2 + y 2 subject to the constraint y = 2x 1. Substitute the expression for the constraint directly into the objective function: z = 2x 2 + y 2 = 2x 2 + (2x 1) 2 = 2x 2 + 4x 2 4x + 1 = 2x 2 4x + 1. This is now a function of only one variable. To find the minimum of z, set 0 = dz dx = 4x 4 which gives x = 1. To determine the nature of this critical point, compute d 2 z dx 2 = 4 which is positive, so x = 1 gives a local minimum. At x = 1 we have y = 2(1) 1 = 1 and then z = (1) 2 + (1) 2 = 1. Find the point on the line 2x + 3y = 4 that is closest to the origin (0,0).

34 30 Optimisation The distance from any point (x, y) in the (x, y)-plane to the origin is D.= (x 0) 2 + (y 0) 2 = x 2 + y 2. We want to minimize D, subject to the constraint that (x, y) lies on the given line, i.e., that 2x + 3y = 4. But the constraint tells us that y = (4 2x)/3, so we can substitute this into the formula for D, getting ( ) 2 4 2x D = x 2 + = [x ] 1/ x + 4x2. 9 Note that originally D was a function of two variables x and y, but the constraint has enabled us to simplify D to a function of one variable x. Thus we search for critical points of D by setting This implies that 0 = dd dx = 1 [x = 1 2x x 9 2 [ ] 1/2. x x+4x2 9 0 = 2x + ] 1/2 [ 16 16x + 4x2 2x + 9 ] x x, i.e., 0 = 18x + ( x), 9 which gives x = 8/13. To verify that x = 8/13 does give the point on the line that is a minimum distance from the origin, we should calculate d 2 D/dx 2 then substitute x = 8/13 and see that we get a positive value, but this is quite a job! Instead we shall simply observe that from the picture it is clear that there definitely is one closest point on the given line, and the only candidate that calculus produces for that point is x = 8/13, so it must indeed be the closest point.

35 Applications to economics 31 A simpler solution: We ran into a lot of algebra in our derivatives because of the square root in D. Note however that whatever value of (x, y) minimizes D will also minimize D 2 because D 0. Thus let s solve the problem again by considering D 2 = E (say) instead of D. That is, we want to minimize E.= x 2 + y 2, subject to the constraint that 2x + 3y = 4. As before y = (4 2x)/3, so ( ) 2 4 2x E = x 2 + = x x + 4x Now set 0 = de dx = 2x x 9 which gives x = 8/13. Furthermore, = 18x x 9 d 2 E dx 2 = > 0 = 26x 16 9 so x = 8/13 does give a minimum of E (recall that in our first solution to this problem we balked at finding d 2 D/dx 2 because it would be so complicated)., Exercises a. Find the shortest distance from the point (1, 0, 2) to the plane x+2y+z = 4. b. Find the point on the plane 2x y + 2z = 16 that is closest to the origin. Ans: (32/9, 16/9, 32/9). c. Find the shortest distance from the point (2, 2, 0) to the plane 6x + 3y 3z = 2. Ans: 24/9. d. Find the points on the surface z 2 = xy + 1 that are closest to the origin. Ans: (0, 0, 1) and (0, 0, 1). e. Find three positive numbers whose sum is 100 and whose product is a maximum. Ans: 100/3, 100/3, 100/3. f. Find three positive numbers whose sum is 120 such that the sum of their products taken two at a time is a maximum. Ans: 40, 40, 40. Applications to economics Production functions A firm wishes to maximize output Q = f(k, L) which depends on capital K and labour L. Suppose the unit cost of capital is P K and the unit cost of labour if P L. Then, using K units of capital and L units of labour, the total cost is P K K + P L L.

36 32 Optimisation If the firm has a fixed amount M to spend on inputs, then P K K + P L L = M. (4.1) Thus the problem for the firm is to maximize Q = f(k, L) subject to the constraint P K K + P L L = M. Here Q, K, L are variables while P K, P L and M are known constants. We solve this problem as in Section 4: from the constraint one gets easily ( ) PL K = L + M (4.2) P K P K and consequently Q = f(k, L) can be reduced to a function of one variable L. To finish the analysis of the problem, we would need a precise formula for f(k, L). Exercises a. A firm s production function is given by Q = 2K 1/2 L 1/2 where K is capital and L is labour. The unit capital and labour costs are e4 and e3 respectively. Find the values of K and L that minimize the total input cost if the firm is contracted to provide 160 units of output. Graphical interpretation The isocost curve (straight line in this example) is tangent to the isoquant curve that yields the maximum output. The K axis is vertical and the L axis is horizontal. The isocost curve (a straight line in this example) is drawn;

37 Applications to economics 33 along it the total input cost remains constant and this is the maximum cost that the firm is allowed to incur. We want to maximize output subject to this constraint, i.e., subject to the restriction that our solution (K, L) must lie on the isocost curve. Three isoquant curves are drawn above; along each isoquant the output is constant, and the output is larger as the curves move to the right and upwards (i.e., to the north-east). Thus we want to be on the isoquant curve that is furthest to the north-east, subject to the constraint that we must remain on the isocost line. Hence the isoquant curve that maximizes output is the one furthest to the north-east that just touches the isocost line, i.e., the isoquant and isocost curves are tangential at the point (K, L) where output is maximized. We now interpret this geometric observation in terms of economic quantities. In (3.1) and (3.2) the marginal rate of technical substitution on the isoquant is seen to satisfy dk dl = MRTS.= MP L, MP K where dk/dl is also the slope of the isoquant. But from (4.2) the slope of the isocost line is P L P K. Our argument above says that the slopes of the isoquant curve and isocost line are equal at the optimal output level, so dk dl = P L P K, This is usually rearranged into the form MP L P L i.e., MP L MP K = P L P K. = MP K P K : (4.3) at optimal output, the ratio of marginal product to price is the same for all inputs. We shall derive this formula in a different way in Section 5. Utility functions The analysis above for production functions can be replicated for utility functions, as we now show. Suppose that an individual s utility function is U(x 1, x 2 ) where x 1 and x 2 are the amounts of goods G 1 and G 2 purchased. Let P 1 and P 2 be the unit prices of these goods. Let M be the (fixed) budget that the individual can spend on G 1 and G 2. Then P 1 x 1 + P 2 x 2 = M (4.4) and we are trying to maximize U(x 1, x 2 ) subject to the constraint (4.4). But this is exactly the same mathematical formulation as maximizing Q = f(k, L) subject to the constraint (4.1), which we considered at the start of