Areas of Tropezoids, Rhombuses, and Kites
|
|
|
- Naomi Short
- 5 years ago
- Views:
Transcription
1 102 Areas of Tropezoids, Rhombuses, and Kites MathemaHcs Florida Standards MAFS.912.G-MG.1.1 Use geometric shapes, their measures, and their properties to describe objects. MP1. MP3, MP 4,MP6 Objective To find the area of a trapezoid, rhombus, or kite Getting Ready! Rearranging figures into familiar shapes is an example of the Solve a Simpler Problem strategy. Drow o tropezotd on a sheet of graph poper. Label the bases bj and bg. Draw its midsegment. Cut out the trapezoid. and then cut it along the midsegment. Rotate the top part of the trapezoid 180 so that bi ond bg now form one long base. How can you use this new figure to find the area of the trapezoid? Explain your reasoning. PRA^Icfe^S Understanding You can find the area of a trapezoid when you know its height and the lengths of its bases. ^ Lesson Vocabulary height of a trapezoid The height of a trapezoid is the perpendicular distance between the bases. Theorem 10-4 Area of o Trapezoid The area of a trapezoid is half the product of the height and the sum of the bases. A = ^h{bi + b2) Which borders of Nevada can you use as the bases of a trapezoid? The two parallel sides of Nevada form the bases of a trapezoid. Problem 1 Area of a Trapezoid Geography What is the approximate area of Nevada? A = + ^2) Use the formula for area of a trapezoid. = (309)( ) Substitute 309 for h, 205 for bi, and 511 for 62- = 110,622 Simplify. The area of Nevada is about 110,600 mi^. Gotit? 1. What is the area of a trapezoid with height * 7 cm and bases 12 cm and 15 cm? 205 mi 309 mi (s) Reno ^ Carson City 511 ml C PowerGeometry.com Lesson 10-2 Areas of Trapezoids, Rhombuses, and Kites 623
2 Problem 2 Finding Area Using a Right Triangle How are the sides related in a triangle? The length of the hypotenuse Is 2 times the length of the shorter leg, and the longer leg Is V3 times the length of the shorter leg. What is the area of trapezoid PQRSl You can draw an altitude that divides the trapezoid into a rectangle and a triangle. Since the opposite sides of a rectangle are congruent, the longer base of the trapezoid is divided into segments of lengths 2 m and 5 m. h = 2V3 A = + fj2) = (2V5)(7-f-5) = 12V3 longer leg = shorter leg Use the trapezoid area formula. Substitute 2\/3 for h, 1 for bi, and 5for /)2. Simplify. The area of trapezoid PQRS is 12 Vs m^. S 5m /? 7 m 5 5m ft P 2m 5m 0 Got It? 2. Reasoning In Problem 2, suppose h decreases so that map = 45 while angles R and Q and the bases stay the same. What is the area of trapezoid PQRSl Essential Understanding You can find the area of a rhombus or a kite when you know the lengths of its diagonals. Theorem 10-5 Area of o Rhombus or o Kite The area of a rhombus or a kite Is half the product of the lengths of its diagonals. A Rhombus Kite V Problem 3 Finding the Area of a Kite Do you need to know the side lengths of the kite to find its area? No. You only need the lengths of the diagonals. What is the area of kite KLMNl Find the lengths of the two diagonals: ii;:m = = 7m and IN = = 6 m. A = k(l\d2 Use the formula for area of a kite. = Substitute 7 for dy and 6 for di- = 21 Simplify. The area of kite KLMN is 21 m^. Got It? 3. What is the area of a kite with diagonals that are 12 in. and 9 in. long? 624 Chapter 10 Area
3 TV.*:' " How can you find the length of >^? AB is a leg of right AABC. You can use the Pythagorean Theorem, a2 + /j2 _ (-2^ fjpj its length. Problem 4\ Finding the Area of a Rhombus Car Pooling Ihe High OccupancyVehicle(HOV) lane is marked by a series of "diamonds " or rhombuses painted on the pavement. What is the area of the HOV lane diamond shown at the right? AABC is a right triangle. Using the Pythagorean Theorem, AB = Vb.S^ 2.5^ = 6. Since the diagonals of a rhombus bisect each other, the diagonals of the HOV lane diamond are 5 ft and 12 ft. A = hdido 2"1"2 = (5X12) = 30 Use the formula for area of a rhombus. Substitute 5 for d] and 12 for ^2. Simplify. The area of the HOV lane diamond is 30 Got It? 4. A rhombus has sides 10 cm long. ^ If the longer diagonal is 16 cm, what is the area of the rhombus? & Lesson Check Do you know HOW? Find the area of each figure. Do you UNDERSTAND? MATHEMATICAL PRACTICES 7. Vocabulary Can a trapezoid and a parallelogram with the same base and height have the same area? Explain. ' 8 n. 27 in. 3-3 ft 8. Reasoning Do you need to know all the side lengths to find the area of a trapezoid? Reasoning Can you find the area of a rhombus if you only know the lengths of its sides? Explain. 10. Reasoning Do you need to know the lengths of the sides to find the area of a kite? Explain. 20 m 1 cm sowerg eo metry.co m Lesson 10-2 Areas of Trapezoids, Rhombuses, and Kites 625
4 Practice and Problem-Solving Exercises MATHEMATICAL PRACTICES Practice Find the area of each trapezoid ^ See Problem in cm in. I 38 In. j 8.5 cm 9.7 cm 18 ft 1] Vft 6 ft 14. Find the area of a trapezoid with bases 12 cm and 18 cm and height 10 cm. 15. Find the area of a trapezoid with bases 2 ft and 3 ft and height ft. 16. Geography The border of Tennessee resembles a trapezoid with bases 340 mi and 440 mi and height 110 mi. Estimate the area of Tennessee by finding the area of the trapezoid. Find the area of each trapezoid. If your answer is not an integer, leave it in simplest radical form. ^ See Problem ft, 6 ft L 3 ft ft/ /eo" 15 ft r 19. Find the area of each kite. 20.,2 in m/ 3 3 m 4 nn\. 22. /4 ft ^ See Problem 3. 6ft\ 4ft\ Find the area of each rhombus. ^ See Problem \loin. y/o in. 26. Think About a Plan A trapezoid has two right angles, 12-m and 18-m bases, and an 8-m height. Sketch the trapezoid and find its perimeter and area. Are the right angles consecutive or opposite angles? How does knowing the height help you find the perimeter? 626 Chapter 10 Area
5 27. Metallurgy The end of a gold bar has the shape of a trapezoid with the measurements shown. Find the area of the end. 28. Open-Ended Draw a kite. Measure the lengths of its diagonals. Find its area. Find the area of each trapezoid to the nearest tenth cm 3 cm Jl 4 cm 1 cm ft 30 1-^9 ft 6.9 cm 4.4 cm 9.2-cm y Coordinate Geometry Find the area of quadrilateral QRST. 33. y Ir -4 n T 2 S.1 X What is the area of the kite at the right? Ca> 90 m^ CO 135 m^ CO 108 m2 CO a. Coordinate Geometry Graph the lines r = 0, x = 6, y = 0, and y = x + 4. b. What type of quadrilateral do the lines form? c. Find the area of the quadrilateral. Find the area of each rhombus. Leave your answer in simplest radical form. 39. Z in. 40. Visualization The kite has diagonals dj and congruent to the sides of the rectangle. Explain why the area of the kite is did2-41. Draw a trapezoid. Label its bases bi and >2 and its height h. Then draw a diagonal of the trapezoid. a. Write equations for the area of each of the two triangles formed. b. Writing Explain how you can justify the trapezoid area formula using the areas of the two triangles. d2 C PowerGeometry.com Lesson 10-2 Areas of Trapezoids, Rhombuses, and Kites 627
6 challenge 42. Algebra One base of a trapezoid is twice the other. The height is the average of the two bases. The area is 324 cm^. Find the height and the bases. {Hint: Let the smaller base be x) 43. Sports Ty wants to paint one side of the skateboarding ramp he built. The ramp is 4 m wide. Its surface is modeled by the equation y = 0.25^:^. Use the trapezoids and triangles y = 0.25x2 shown to estimate the area to be painted. 44. In trapezoid ABCD at the right, AB 1 DC. Find the area of ABCD. Standardized Test Prep SAT/Aa 45. The area of a kite is 120 cm^. The length of one diagonal is 20 cm. What is the length of the other diagonal? CS5 12 cm dz) 20 cm CO 24 cm CO 48 cm 46. AABC ~ AXYZ. AB = 6,BC = 3, and CA = 7. Which of the following are NOT possible dimensions of AXYZl CE:>X1'=3, yz= 1.5,ZX=3.5 Ch:)XY= 10, YZ= 7, ZX= 11 CO xy=9, YZ=4.5,ZX'= 10.5 CL^ XY= 18. YZ = 9, ZX= 21 Short.Response 47. Draw an angle. Construct a congruent angle and its bisector. r Mixed Review 48. Find the area of a right isosceles triangle that has one leg of length 12 cm. 49. A right isosceles triangle has area ft^. Find the length of each leg. 50. Find the measure of an interior angle of a regular nonagon. Get Ready! To prepare for Lesson 10-3, do Exercises Find the area of each regular polygon. Leave radicals in simplest form. ^ See Lesson ^ See Lesson 6-1. ^ See Lesson cm ' 10 ft 628 Chapter 10 Area
6-1. Angles of Polygons. Lesson 6-1. What You ll Learn. Active Vocabulary
 6-1 Angles of Polygons What You ll Learn Skim Lesson 6-1. Predict two things that you expect to learn based on the headings and figures in the lesson. 1. 2. Lesson 6-1 Active Vocabulary diagonal New Vocabulary
6-1 Angles of Polygons What You ll Learn Skim Lesson 6-1. Predict two things that you expect to learn based on the headings and figures in the lesson. 1. 2. Lesson 6-1 Active Vocabulary diagonal New Vocabulary
Objective To find the perimeters and areas of similar polygons
 104 Perimeters and Areas of Similar Figures Mathematics Florida Standards Prepares for MAFS.912.G-GMD.1.3 Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems. MP 1. MP 3,
104 Perimeters and Areas of Similar Figures Mathematics Florida Standards Prepares for MAFS.912.G-GMD.1.3 Use volume formulas for cylinders, pyramids, cones, and spheres to solve problems. MP 1. MP 3,
GEO: Sem 1 Unit 1 Review of Geometry on the Coordinate Plane Section 1.6: Midpoint and Distance in the Coordinate Plane (1)
 GEO: Sem 1 Unit 1 Review of Geometr on the Coordinate Plane Section 1.6: Midpoint and Distance in the Coordinate Plane (1) NAME OJECTIVES: WARM UP Develop and appl the formula for midpoint. Use the Distance
GEO: Sem 1 Unit 1 Review of Geometr on the Coordinate Plane Section 1.6: Midpoint and Distance in the Coordinate Plane (1) NAME OJECTIVES: WARM UP Develop and appl the formula for midpoint. Use the Distance
UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet
 Name Period Date UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet 24.1 The Pythagorean Theorem Explore the Pythagorean theorem numerically, algebraically, and geometrically. Understand a proof
Name Period Date UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet 24.1 The Pythagorean Theorem Explore the Pythagorean theorem numerically, algebraically, and geometrically. Understand a proof
Lesson 1 Area of Parallelograms
 NAME DATE PERIOD Lesson 1 Area of Parallelograms Words Formula The area A of a parallelogram is the product of any b and its h. Model Step 1: Write the Step 2: Replace letters with information from picture
NAME DATE PERIOD Lesson 1 Area of Parallelograms Words Formula The area A of a parallelogram is the product of any b and its h. Model Step 1: Write the Step 2: Replace letters with information from picture
11.2 Areas of Trapezoids,
 11. Areas of Trapezoids, Rhombuses, and Kites Goal p Find areas of other types of quadrilaterals. Your Notes VOCABULARY Height of a trapezoid THEOREM 11.4: AREA OF A TRAPEZOID b 1 The area of a trapezoid
11. Areas of Trapezoids, Rhombuses, and Kites Goal p Find areas of other types of quadrilaterals. Your Notes VOCABULARY Height of a trapezoid THEOREM 11.4: AREA OF A TRAPEZOID b 1 The area of a trapezoid
Geometry Topic 4 Quadrilaterals and Coordinate Proof
 Geometry Topic 4 Quadrilaterals and Coordinate Proof MAFS.912.G-CO.3.11 In the diagram below, parallelogram has diagonals and that intersect at point. Which expression is NOT always true? A. B. C. D. C
Geometry Topic 4 Quadrilaterals and Coordinate Proof MAFS.912.G-CO.3.11 In the diagram below, parallelogram has diagonals and that intersect at point. Which expression is NOT always true? A. B. C. D. C
Downloaded from
 1 IX Mathematics Chapter 8: Quadrilaterals Chapter Notes Top Definitions 1. A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order. 2. A diagonal
1 IX Mathematics Chapter 8: Quadrilaterals Chapter Notes Top Definitions 1. A quadrilateral is a closed figure obtained by joining four points (with no three points collinear) in an order. 2. A diagonal
Warm-Up Exercises. Find the value of x. 1. ANSWER 65 ANSWER 120
 Warm-Up Exercises Find the value of x. 1. 65 2. 120 Warm-Up Exercises Find the value of x. 3. 70 EXAMPLE Warm-Up 1Exercises Identify quadrilaterals Quadrilateral ABCD has at least one pair of opposite
Warm-Up Exercises Find the value of x. 1. 65 2. 120 Warm-Up Exercises Find the value of x. 3. 70 EXAMPLE Warm-Up 1Exercises Identify quadrilaterals Quadrilateral ABCD has at least one pair of opposite
Date: Period: Quadrilateral Word Problems: Review Sheet
 Name: Quadrilateral Word Problems: Review Sheet Date: Period: Geometry Honors Directions: Please answer the following on a separate sheet of paper. Completing this review sheet will help you to do well
Name: Quadrilateral Word Problems: Review Sheet Date: Period: Geometry Honors Directions: Please answer the following on a separate sheet of paper. Completing this review sheet will help you to do well
Geometry Chapter 8 8-5: USE PROPERTIES OF TRAPEZOIDS AND KITES
 Geometry Chapter 8 8-5: USE PROPERTIES OF TRAPEZOIDS AND KITES Use Properties of Trapezoids and Kites Objective: Students will be able to identify and use properties to solve trapezoids and kites. Agenda
Geometry Chapter 8 8-5: USE PROPERTIES OF TRAPEZOIDS AND KITES Use Properties of Trapezoids and Kites Objective: Students will be able to identify and use properties to solve trapezoids and kites. Agenda
3.3. You wouldn t think that grasshoppers could be dangerous. But they can damage
 Grasshoppers Everywhere! Area and Perimeter of Parallelograms on the Coordinate Plane. LEARNING GOALS In this lesson, you will: Determine the perimeter of parallelograms on a coordinate plane. Determine
Grasshoppers Everywhere! Area and Perimeter of Parallelograms on the Coordinate Plane. LEARNING GOALS In this lesson, you will: Determine the perimeter of parallelograms on a coordinate plane. Determine
Geometry - Chapter 6 Review
 Class: Date: Geometry - Chapter 6 Review 1. Find the sum of the measures of the angles of the figure. 4. Find the value of x. The diagram is not to scale. A. 1260 B. 900 C. 540 D. 720 2. The sum of the
Class: Date: Geometry - Chapter 6 Review 1. Find the sum of the measures of the angles of the figure. 4. Find the value of x. The diagram is not to scale. A. 1260 B. 900 C. 540 D. 720 2. The sum of the
The area A of a trapezoid is one half the product of the height h and the sum of the lengths of its bases, b 1 and b 2.
 ALGEBRA Find each missing length. 21. A trapezoid has a height of 8 meters, a base length of 12 meters, and an area of 64 square meters. What is the length of the other base? The area A of a trapezoid
ALGEBRA Find each missing length. 21. A trapezoid has a height of 8 meters, a base length of 12 meters, and an area of 64 square meters. What is the length of the other base? The area A of a trapezoid
MEA 501 LESSON _NOTES Period. CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must MEA 301 Compute the perimeter of polygons when all
 MEA 501 LESSON _NOTES Period Name CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must MEA 301 Compute the perimeter of polygons when all attain mastery at this level side lengths are given MEA 302 Compute
MEA 501 LESSON _NOTES Period Name CRS SKILL LEVEL DESCRIPTION Level 1 ALL students must MEA 301 Compute the perimeter of polygons when all attain mastery at this level side lengths are given MEA 302 Compute
1. Convert 60 mi per hour into km per sec. 2. Convert 3000 square inches into square yards.
 ACT Practice Name Geo Unit 3 Review Hour Date Topics: Unit Conversions Length and Area Compound shapes Removing Area Area and Perimeter with radicals Isosceles and Equilateral triangles Pythagorean Theorem
ACT Practice Name Geo Unit 3 Review Hour Date Topics: Unit Conversions Length and Area Compound shapes Removing Area Area and Perimeter with radicals Isosceles and Equilateral triangles Pythagorean Theorem
16. DOK 1, I will succeed." In this conditional statement, the underlined portion is
 Geometry Semester 1 REVIEW 1. DOK 1 The point that divides a line segment into two congruent segments. 2. DOK 1 lines have the same slope. 3. DOK 1 If you have two parallel lines and a transversal, then
Geometry Semester 1 REVIEW 1. DOK 1 The point that divides a line segment into two congruent segments. 2. DOK 1 lines have the same slope. 3. DOK 1 If you have two parallel lines and a transversal, then
Catty Corner. Side Lengths in Two and. Three Dimensions
 Catty Corner Side Lengths in Two and 4 Three Dimensions WARM UP A 1. Imagine that the rectangular solid is a room. An ant is on the floor situated at point A. Describe the shortest path the ant can crawl
Catty Corner Side Lengths in Two and 4 Three Dimensions WARM UP A 1. Imagine that the rectangular solid is a room. An ant is on the floor situated at point A. Describe the shortest path the ant can crawl
Unit 6 Quadrilaterals
 Unit 6 Quadrilaterals ay lasswork ay Homework Monday Properties of a Parallelogram 1 HW 6.1 11/13 Tuesday 11/14 Proving a Parallelogram 2 HW 6.2 Wednesday 11/15 Thursday 11/16 Friday 11/17 Monday 11/20
Unit 6 Quadrilaterals ay lasswork ay Homework Monday Properties of a Parallelogram 1 HW 6.1 11/13 Tuesday 11/14 Proving a Parallelogram 2 HW 6.2 Wednesday 11/15 Thursday 11/16 Friday 11/17 Monday 11/20
8-1 Similarity in Right Triangles
 8-1 Similarity in Right Triangles In this chapter about right triangles, you will be working with radicals, such as 19 and 2 5. radical is in simplest form when: 1. No perfect square factor other then
8-1 Similarity in Right Triangles In this chapter about right triangles, you will be working with radicals, such as 19 and 2 5. radical is in simplest form when: 1. No perfect square factor other then
1. Take out a piece of notebook paper and make a hot dog fold over from the right side over to the pink line. Foldable
 Four sided polygon 1. Take out a piece of notebook paper and make a hot dog fold over from the right side over to the pink line. Foldable Foldable The fold crease 2. Now, divide the right hand section
Four sided polygon 1. Take out a piece of notebook paper and make a hot dog fold over from the right side over to the pink line. Foldable Foldable The fold crease 2. Now, divide the right hand section
SOLUTION: The trapezoid ABCD is an isosceles trapezoid. So, each pair of base angles is congruent. Therefore,
 Find each measure. 1. The trapezoid ABCD is an isosceles trapezoid. So, each pair of base angles is congruent. Therefore, 2. WT, if ZX = 20 and TY = 15 The trapezoid WXYZ is an isosceles trapezoid. So,
Find each measure. 1. The trapezoid ABCD is an isosceles trapezoid. So, each pair of base angles is congruent. Therefore, 2. WT, if ZX = 20 and TY = 15 The trapezoid WXYZ is an isosceles trapezoid. So,
Geometry Unit 6 Note Sheets. Name of Lesson. 6.1 Angles of Polygons 1.5 days. 6.2 Parallelograms 1 day. 6.3 Tests for Parallelograms 1.
 Date Name of Lesson 6.1 Angles of Polygons 1.5 days 6.2 Parallelograms 1 day 6.3 Tests for Parallelograms 1.5 days Quiz 6.1-6.3 0.5 days 6.4 Rectangles 1 day 6.5 Rhombi and Squares 1 day 6.6 Trapezoids
Date Name of Lesson 6.1 Angles of Polygons 1.5 days 6.2 Parallelograms 1 day 6.3 Tests for Parallelograms 1.5 days Quiz 6.1-6.3 0.5 days 6.4 Rectangles 1 day 6.5 Rhombi and Squares 1 day 6.6 Trapezoids
Geometry Mrs. Crocker Spring 2014 Final Exam Review
 Name: Mod: Geometry Mrs. Crocker Spring 2014 Final Exam Review Use this exam review to complete your flip book and to study for your upcoming exam. You must bring with you to the exam: 1. Pencil, eraser,
Name: Mod: Geometry Mrs. Crocker Spring 2014 Final Exam Review Use this exam review to complete your flip book and to study for your upcoming exam. You must bring with you to the exam: 1. Pencil, eraser,
Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions.
 Student Outcomes Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions. Lesson Notes It is recommended that students have access to a calculator as they work
Student Outcomes Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions. Lesson Notes It is recommended that students have access to a calculator as they work
6-6 Trapezoids and Kites. CCSS SENSE-MAKING If WXYZ is a kite, find each measure. 25. WP
 CCSS SENSE-MAKING If WXYZ is a kite, find each measure. 25. WP By the Pythagorean Theorem, WP 2 = WX 2 XP 2 = 6 2 4 2 = 20 27. A kite can only have one pair of opposite congruent angles and Let m X = m
CCSS SENSE-MAKING If WXYZ is a kite, find each measure. 25. WP By the Pythagorean Theorem, WP 2 = WX 2 XP 2 = 6 2 4 2 = 20 27. A kite can only have one pair of opposite congruent angles and Let m X = m
FSA Geometry EOC Getting ready for. Circles, Geometric Measurement, and Geometric Properties with Equations.
 Getting ready for. FSA Geometry EOC Circles, Geometric Measurement, and Geometric Properties with Equations 2014-2015 Teacher Packet Shared by Miami-Dade Schools Shared by Miami-Dade Schools MAFS.912.G-C.1.1
Getting ready for. FSA Geometry EOC Circles, Geometric Measurement, and Geometric Properties with Equations 2014-2015 Teacher Packet Shared by Miami-Dade Schools Shared by Miami-Dade Schools MAFS.912.G-C.1.1
Worksheet 10 Memorandum: Construction of Geometric Figures. Grade 9 Mathematics
 Worksheet 10 Memorandum: Construction of Geometric Figures Grade 9 Mathematics For each of the answers below, we give the steps to complete the task given. We ve used the following resources if you would
Worksheet 10 Memorandum: Construction of Geometric Figures Grade 9 Mathematics For each of the answers below, we give the steps to complete the task given. We ve used the following resources if you would
Geometry 2001 part 1
 Geometry 2001 part 1 1. Point is the center of a circle with a radius of 20 inches. square is drawn with two vertices on the circle and a side containing. What is the area of the square in square inches?
Geometry 2001 part 1 1. Point is the center of a circle with a radius of 20 inches. square is drawn with two vertices on the circle and a side containing. What is the area of the square in square inches?
Geometry. a) Rhombus b) Square c) Trapezium d) Rectangle
 Geometry A polygon is a many sided closed shape. Four sided polygons are called quadrilaterals. Sum of angles in a quadrilateral equals 360. Parallelogram is a quadrilateral where opposite sides are parallel.
Geometry A polygon is a many sided closed shape. Four sided polygons are called quadrilaterals. Sum of angles in a quadrilateral equals 360. Parallelogram is a quadrilateral where opposite sides are parallel.
0809ge. Geometry Regents Exam Based on the diagram below, which statement is true?
 0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB # AC. The measure of!b is 40. 1) a! b 2) a! c 3) b! c 4) d! e What is the measure of!a? 1) 40 2) 50 3) 70
0809ge 1 Based on the diagram below, which statement is true? 3 In the diagram of ABC below, AB # AC. The measure of!b is 40. 1) a! b 2) a! c 3) b! c 4) d! e What is the measure of!a? 1) 40 2) 50 3) 70
(A) Circle (B) Polygon (C) Line segment (D) None of them (A) (B) (C) (D) (A) Understanding Quadrilaterals <1M>
 Understanding Quadrilaterals 1.A simple closed curve made up of only line segments is called a (A) Circle (B) Polygon (C) Line segment (D) None of them 2.In the following figure, which of the polygon
Understanding Quadrilaterals 1.A simple closed curve made up of only line segments is called a (A) Circle (B) Polygon (C) Line segment (D) None of them 2.In the following figure, which of the polygon
3 Kevin s work for deriving the equation of a circle is shown below.
 June 2016 1. A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation?
June 2016 1. A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation?
AREA See the Math Notes box in Lesson for more information about area.
 AREA..1.. After measuring various angles, students look at measurement in more familiar situations, those of length and area on a flat surface. Students develop methods and formulas for calculating the
AREA..1.. After measuring various angles, students look at measurement in more familiar situations, those of length and area on a flat surface. Students develop methods and formulas for calculating the
(A) Circle (B) Polygon (C) Line segment (D) None of them
 Understanding Quadrilaterals 1.The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60 degree. Find the angles of the parallelogram.
Understanding Quadrilaterals 1.The angle between the altitudes of a parallelogram, through the same vertex of an obtuse angle of the parallelogram is 60 degree. Find the angles of the parallelogram.
Discussion: With a partner, discuss what you believe a parallelogram is? Parallelogram Definition:
 Name: Ms. Ayinde Date: Geometry CC 4.2: Properties of Parallelograms Objective: To recognize and apply properties of sides, angles, and diagonals of parallelograms. To determine the area and perimeter
Name: Ms. Ayinde Date: Geometry CC 4.2: Properties of Parallelograms Objective: To recognize and apply properties of sides, angles, and diagonals of parallelograms. To determine the area and perimeter
Geometry by Jurgensen, Brown and Jurgensen Postulates and Theorems from Chapter 1
 Postulates and Theorems from Chapter 1 Postulate 1: The Ruler Postulate 1. The points on a line can be paired with the real numbers in such a way that any two points can have coordinates 0 and 1. 2. Once
Postulates and Theorems from Chapter 1 Postulate 1: The Ruler Postulate 1. The points on a line can be paired with the real numbers in such a way that any two points can have coordinates 0 and 1. 2. Once
Geometer s Skethchpad 8th Grade Guide to Learning Geometry
 Geometer s Skethchpad 8th Grade Guide to Learning Geometry This Guide Belongs to: Date: Table of Contents Using Sketchpad - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
Geometer s Skethchpad 8th Grade Guide to Learning Geometry This Guide Belongs to: Date: Table of Contents Using Sketchpad - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -
3 In the diagram below, the vertices of DEF are the midpoints of the sides of equilateral triangle ABC, and the perimeter of ABC is 36 cm.
 1 In the diagram below, ABC XYZ. 3 In the diagram below, the vertices of DEF are the midpoints of the sides of equilateral triangle ABC, and the perimeter of ABC is 36 cm. Which two statements identify
1 In the diagram below, ABC XYZ. 3 In the diagram below, the vertices of DEF are the midpoints of the sides of equilateral triangle ABC, and the perimeter of ABC is 36 cm. Which two statements identify
Squares and Square Roots Algebra 11.1
 Squares and Square Roots Algebra 11.1 To square a number, multiply the number by itself. Practice: Solve. 1. 1. 0.6. (9) 4. 10 11 Squares and Square Roots are Inverse Operations. If =y then is a square
Squares and Square Roots Algebra 11.1 To square a number, multiply the number by itself. Practice: Solve. 1. 1. 0.6. (9) 4. 10 11 Squares and Square Roots are Inverse Operations. If =y then is a square
The Pythagorean Theorem 8.6.C
 ? LESSON 8.1 The Pythagorean Theorem ESSENTIAL QUESTION Expressions, equations, and relationships 8.6.C Use models and diagrams to explain the Pythagorean Theorem. 8.7.C Use the Pythagorean Theorem...
? LESSON 8.1 The Pythagorean Theorem ESSENTIAL QUESTION Expressions, equations, and relationships 8.6.C Use models and diagrams to explain the Pythagorean Theorem. 8.7.C Use the Pythagorean Theorem...
Indicate whether the statement is true or false.
 MATH 121 SPRING 2017 - PRACTICE FINAL EXAM Indicate whether the statement is true or false. 1. Given that point P is the midpoint of both and, it follows that. 2. If, then. 3. In a circle (or congruent
MATH 121 SPRING 2017 - PRACTICE FINAL EXAM Indicate whether the statement is true or false. 1. Given that point P is the midpoint of both and, it follows that. 2. If, then. 3. In a circle (or congruent
11.2 Areas of Trapezoids and Kites
 Investigating g Geometry ACTIVITY Use before Lesson 11.2 11.2 Areas of Trapezoids and Kites MATERIALS grap paper straigtedge scissors tape Q U E S T I O N How can you use a parallelogram to find oter areas?
Investigating g Geometry ACTIVITY Use before Lesson 11.2 11.2 Areas of Trapezoids and Kites MATERIALS grap paper straigtedge scissors tape Q U E S T I O N How can you use a parallelogram to find oter areas?
FINAL REVIEW. 1) Always, Sometimes, or Never. If you answer sometimes, give an example for when it is true and an example for when it is not true.
 FINL RVIW 1) lways, Sometimes, or Never. If you answer sometimes, give an eample for when it is true and an eample for when it is not true. a) rhombus is a square. b) square is a parallelogram. c) oth
FINL RVIW 1) lways, Sometimes, or Never. If you answer sometimes, give an eample for when it is true and an eample for when it is not true. a) rhombus is a square. b) square is a parallelogram. c) oth
June 2016 Regents GEOMETRY COMMON CORE
 1 A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation? 4) 2
1 A student has a rectangular postcard that he folds in half lengthwise. Next, he rotates it continuously about the folded edge. Which three-dimensional object below is generated by this rotation? 4) 2
0810ge. Geometry Regents Exam y # (x $ 3) 2 % 4 y # 2x $ 5 1) (0,%4) 2) (%4,0) 3) (%4,%3) and (0,5) 4) (%3,%4) and (5,0)
 0810ge 1 In the diagram below, ABC! XYZ. 3 In the diagram below, the vertices of DEF are the midpoints of the sides of equilateral triangle ABC, and the perimeter of ABC is 36 cm. Which two statements
0810ge 1 In the diagram below, ABC! XYZ. 3 In the diagram below, the vertices of DEF are the midpoints of the sides of equilateral triangle ABC, and the perimeter of ABC is 36 cm. Which two statements
1. 1 Square Numbers and Area Models (pp. 6-10)
 Math 8 Unit 1 Notes Name: 1. 1 Square Numbers and Area Models (pp. 6-10) square number: the product of a number multiplied by itself; for example, 25 is the square of 5 perfect square: a number that is
Math 8 Unit 1 Notes Name: 1. 1 Square Numbers and Area Models (pp. 6-10) square number: the product of a number multiplied by itself; for example, 25 is the square of 5 perfect square: a number that is
6.00 Trigonometry Geometry/Circles Basics for the ACT. Name Period Date
 6.00 Trigonometry Geometry/Circles Basics for the ACT Name Period Date Perimeter and Area of Triangles and Rectangles The perimeter is the continuous line forming the boundary of a closed geometric figure.
6.00 Trigonometry Geometry/Circles Basics for the ACT Name Period Date Perimeter and Area of Triangles and Rectangles The perimeter is the continuous line forming the boundary of a closed geometric figure.
Unit 6: Quadrilaterals
 Name: Period: Unit 6: Quadrilaterals Geometry Honors Homework Section 6.1: Classifying Quadrilaterals State whether each statement is true or false. Justify your response. 1. All squares are rectangles.
Name: Period: Unit 6: Quadrilaterals Geometry Honors Homework Section 6.1: Classifying Quadrilaterals State whether each statement is true or false. Justify your response. 1. All squares are rectangles.
Regents Exam Questions G.G.69: Quadrilaterals in the Coordinate Plane 2
 Regents Exam Questions G.G.69: Quadrilaterals in the Coordinate Plane 2 www.jmap.org Name: G.G.69: Quadrilaterals in the Coordinate Plane 2: Investigate the properties of quadrilaterals in the coordinate
Regents Exam Questions G.G.69: Quadrilaterals in the Coordinate Plane 2 www.jmap.org Name: G.G.69: Quadrilaterals in the Coordinate Plane 2: Investigate the properties of quadrilaterals in the coordinate
Geometry. Warm Ups. Chapter 11
 Geometry Warm Ups Chapter 11 Name Period Teacher 1 1.) Find h. Show all work. (Hint: Remember special right triangles.) a.) b.) c.) 2.) Triangle RST is a right triangle. Find the measure of angle R. Show
Geometry Warm Ups Chapter 11 Name Period Teacher 1 1.) Find h. Show all work. (Hint: Remember special right triangles.) a.) b.) c.) 2.) Triangle RST is a right triangle. Find the measure of angle R. Show
9.5 Properties and Conditions for Kites and Trapezoids
 Name lass ate 9.5 Properties and onditions for Kites and Trapezoids ssential uestion: What are the properties of kites and trapezoids? Resource Locker xplore xploring Properties of Kites kite is a quadrilateral
Name lass ate 9.5 Properties and onditions for Kites and Trapezoids ssential uestion: What are the properties of kites and trapezoids? Resource Locker xplore xploring Properties of Kites kite is a quadrilateral
Honors Geometry Chapter 6 Supplement. Q (4x) (5x)
 Honors Geometry hapter 6 upplement Name: 1. Given: Q m Q = (4x) m Q = (5x) m Q = 40 m Q = 32 Find the value of x, m Q, m Q, m Q Q (4x) (5x) 40 32 2. Given: m = (8x + 20) m = (150 6x) m = (12x + 60) a)
Honors Geometry hapter 6 upplement Name: 1. Given: Q m Q = (4x) m Q = (5x) m Q = 40 m Q = 32 Find the value of x, m Q, m Q, m Q Q (4x) (5x) 40 32 2. Given: m = (8x + 20) m = (150 6x) m = (12x + 60) a)
Lesson 3.1 Duplicating Segments and Angles
 Lesson 3.1 Duplicating Segments and ngles Name eriod Date In Exercises 1 3, use the segments and angles below. omplete the constructions on a separate piece of paper. S 1. Using only a compass and straightedge,
Lesson 3.1 Duplicating Segments and ngles Name eriod Date In Exercises 1 3, use the segments and angles below. omplete the constructions on a separate piece of paper. S 1. Using only a compass and straightedge,
5.3. Area of Polygons and Circles Play Area. My Notes ACTIVITY
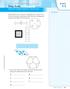 Area of Polygons and Circles SUGGESTED LEARNING STRATEGIES: Think/Pair/Share ACTIVITY 5.3 Pictured below is an aerial view of a playground. An aerial view is the view from above something. Decide what
Area of Polygons and Circles SUGGESTED LEARNING STRATEGIES: Think/Pair/Share ACTIVITY 5.3 Pictured below is an aerial view of a playground. An aerial view is the view from above something. Decide what
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Thursday, August 17, :30 to 3:30 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 17, 2017 12:30 to 3:30 p.m., only Student Name: School Name: The possession or use of any communications
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Thursday, August 17, 2017 12:30 to 3:30 p.m., only Student Name: School Name: The possession or use of any communications
Geometry 1 FINAL REVIEW 2011
 Geometry 1 FINL RVIW 2011 1) lways, Sometimes, or Never. If you answer sometimes, give an eample for when it is true and an eample for when it is not true. a) rhombus is a square. b) square is a parallelogram.
Geometry 1 FINL RVIW 2011 1) lways, Sometimes, or Never. If you answer sometimes, give an eample for when it is true and an eample for when it is not true. a) rhombus is a square. b) square is a parallelogram.
1. Write the angles in order from 2. Write the side lengths in order from
 Lesson 1 Assignment Triangle Inequalities 1. Write the angles in order from 2. Write the side lengths in order from smallest to largest. shortest to longest. 3. Tell whether a triangle can have the sides
Lesson 1 Assignment Triangle Inequalities 1. Write the angles in order from 2. Write the side lengths in order from smallest to largest. shortest to longest. 3. Tell whether a triangle can have the sides
Geometry Unit 5 Practice Test
 Name: Class: Date: ID: X Geometry Unit 5 Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. What is the value of x in the rectangle? Hint: use
Name: Class: Date: ID: X Geometry Unit 5 Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. What is the value of x in the rectangle? Hint: use
Name Date. Chapter 15 Final Review
 Name Date Chapter 15 Final Review Tell whether the events are independent or dependent. Explain. 9) You spin a spinner twice. First Spin: You spin a 2. Second Spin: You spin an odd number. 10) Your committee
Name Date Chapter 15 Final Review Tell whether the events are independent or dependent. Explain. 9) You spin a spinner twice. First Spin: You spin a 2. Second Spin: You spin an odd number. 10) Your committee
#2. Rhombus ABCD has an area of 464 square units. If DB = 18 units, find AC. #3. What is the area of the shaded sector if the measure of <ABC is 80?
 1 Pre-AP Geometry Chapter 12 Test Review Standards/Goals: F.1.a.: I can find the perimeter and area of common plane figures, such as: triangles, quadrilaterals, regular polygons, and irregular figures,
1 Pre-AP Geometry Chapter 12 Test Review Standards/Goals: F.1.a.: I can find the perimeter and area of common plane figures, such as: triangles, quadrilaterals, regular polygons, and irregular figures,
Square Roots and the Pythagorean Theorem
 UNIT 1 Square Roots and the Pythagorean Theorem Just for Fun What Do You Notice? Follow the steps. An example is given. Example 1. Pick a 4-digit number with different digits. 3078 2. Find the greatest
UNIT 1 Square Roots and the Pythagorean Theorem Just for Fun What Do You Notice? Follow the steps. An example is given. Example 1. Pick a 4-digit number with different digits. 3078 2. Find the greatest
Title: Quadrilaterals Aren t Just Squares
 Title: Quadrilaterals ren t Just Squares Brief Overview: This is a collection of the first three lessons in a series of seven lessons studying characteristics of quadrilaterals, including trapezoids, parallelograms,
Title: Quadrilaterals ren t Just Squares Brief Overview: This is a collection of the first three lessons in a series of seven lessons studying characteristics of quadrilaterals, including trapezoids, parallelograms,
Length and area Block 1 Student Activity Sheet
 Block 1 Student Activity Sheet 1. Write the area and perimeter formulas for each shape. 2. What does each of the variables in these formulas represent? 3. How is the area of a square related to the area
Block 1 Student Activity Sheet 1. Write the area and perimeter formulas for each shape. 2. What does each of the variables in these formulas represent? 3. How is the area of a square related to the area
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem
 5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem I. Lesson Objectives: -Students will be able to recall definitions of angles, how to measure angles, and measurement systems
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem I. Lesson Objectives: -Students will be able to recall definitions of angles, how to measure angles, and measurement systems
2016 Geometry Honors Summer Packet
 Name: 2016 Geometry Honors Summer Packet This packet is due the first day of school. It will be graded for completion and effort shown. There will be an assessment on these concepts the first week of school.
Name: 2016 Geometry Honors Summer Packet This packet is due the first day of school. It will be graded for completion and effort shown. There will be an assessment on these concepts the first week of school.
University of Houston High School Mathematics Contest Geometry Exam Spring 2016
 University of Houston High School Mathematics ontest Geometry Exam Spring 016 nswer the following. Note that diagrams may not be drawn to scale. 1. In the figure below, E, =, = 4 and E = 0. Find the length
University of Houston High School Mathematics ontest Geometry Exam Spring 016 nswer the following. Note that diagrams may not be drawn to scale. 1. In the figure below, E, =, = 4 and E = 0. Find the length
Properties of Special Parallelograms
 Properties of Special Parallelograms Lab Summary: This lab consists of four activities that lead students through the construction of a trapezoid. Students then explore the shapes, making conclusions about
Properties of Special Parallelograms Lab Summary: This lab consists of four activities that lead students through the construction of a trapezoid. Students then explore the shapes, making conclusions about
Secondary 2 Unit 7 Test Study Guide
 Class: Date: Secondary 2 Unit 7 Test Study Guide 2014-2015 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which statement can you use to conclude that
Class: Date: Secondary 2 Unit 7 Test Study Guide 2014-2015 Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Which statement can you use to conclude that
The Quadrilateral Detective
 The Quadrilateral Detective a Coordinate Geometry Activity An object might certainly LOOK like a square, but how much information do you really need before you can be absolutely sure that it IS a square?
The Quadrilateral Detective a Coordinate Geometry Activity An object might certainly LOOK like a square, but how much information do you really need before you can be absolutely sure that it IS a square?
Geometry Semester 2 Final Review
 Class: Date: Geometry Semester 2 Final Review Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Each unit on the map represents 5 miles. What
Class: Date: Geometry Semester 2 Final Review Multiple Choice Identify the letter of the choice that best completes the statement or answers the question. 1. Each unit on the map represents 5 miles. What
Analytic Geometry EOC Study Booklet Geometry Domain Units 1-3 & 6
 DOE Assessment Guide Questions (2015) Analytic Geometry EOC Study Booklet Geometry Domain Units 1-3 & 6 Question Example Item #1 Which transformation of ΔMNO results in a congruent triangle? Answer Example
DOE Assessment Guide Questions (2015) Analytic Geometry EOC Study Booklet Geometry Domain Units 1-3 & 6 Question Example Item #1 Which transformation of ΔMNO results in a congruent triangle? Answer Example
Lesson 6.1 Skills Practice
 Lesson 6.1 Skills Practice Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Vocabulary Match each definition to its corresponding term. 1. A mathematical statement
Lesson 6.1 Skills Practice Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Vocabulary Match each definition to its corresponding term. 1. A mathematical statement
All in the Family. b. Use your paper tracing to compare the side lengths of the parallelogram. What appears to be true? Summarize your findings below.
 The quadrilateral family is organized according to the number pairs of sides parallel in a particular quadrilateral. Given a quadrilateral, there are three distinct possibilities: both pairs of opposite
The quadrilateral family is organized according to the number pairs of sides parallel in a particular quadrilateral. Given a quadrilateral, there are three distinct possibilities: both pairs of opposite
Find the area and perimeter of each figure. Round to the nearest tenth if necessary.
 Find the area and perimeter of each figure. Round to the nearest tenth if necessary. 1. Use the Pythagorean Theorem to find the height h, of the parallelogram. Each pair of opposite sides of a parallelogram
Find the area and perimeter of each figure. Round to the nearest tenth if necessary. 1. Use the Pythagorean Theorem to find the height h, of the parallelogram. Each pair of opposite sides of a parallelogram
Investigation. Triangle, Triangle, Triangle. Work with a partner.
 Investigation Triangle, Triangle, Triangle Work with a partner. Materials: centimetre ruler 1-cm grid paper scissors Part 1 On grid paper, draw a large right triangle. Make sure its base is along a grid
Investigation Triangle, Triangle, Triangle Work with a partner. Materials: centimetre ruler 1-cm grid paper scissors Part 1 On grid paper, draw a large right triangle. Make sure its base is along a grid
Semester 1 Final Exam Review
 Target 1: Vocabulary and notation Semester 1 Final Exam Review Name 1. Find the intersection of MN and LO. 2. 3) Vocabulary: Define the following terms and draw a diagram to match: a) Point b) Line c)
Target 1: Vocabulary and notation Semester 1 Final Exam Review Name 1. Find the intersection of MN and LO. 2. 3) Vocabulary: Define the following terms and draw a diagram to match: a) Point b) Line c)
MATH MEASUREMENT AND GEOMETRY
 Students: 1. Students choose appropriate units of measure and use ratios to convert within and between measurement systems to solve problems. 1. Compare weights, capacities, geometric measures, time, and
Students: 1. Students choose appropriate units of measure and use ratios to convert within and between measurement systems to solve problems. 1. Compare weights, capacities, geometric measures, time, and
1.1 The Pythagorean Theorem
 1.1 The Pythagorean Theorem Strand Measurement and Geometry Overall Expectations MGV.02: solve problems involving the measurements of two-dimensional shapes and the volumes of three-dimensional figures;
1.1 The Pythagorean Theorem Strand Measurement and Geometry Overall Expectations MGV.02: solve problems involving the measurements of two-dimensional shapes and the volumes of three-dimensional figures;
8.3 Prove It! A Practice Understanding Task
 15 8.3 Prove It! A Practice Understanding Task In this task you need to use all the things you know about quadrilaterals, distance, and slope to prove that the shapes are parallelograms, rectangles, rhombi,
15 8.3 Prove It! A Practice Understanding Task In this task you need to use all the things you know about quadrilaterals, distance, and slope to prove that the shapes are parallelograms, rectangles, rhombi,
Name Period Date. GEOMETRY AND MEASURESUREMENT Student Pages for Packet 6: Drawings and Constructions
 Name Period Date GEOMETRY AND MEASURESUREMENT Student Pages for Packet 6: Drawings and Constructions GEO6.1 Geometric Drawings Review geometric notation and vocabulary. Use a compass and a ruler to make
Name Period Date GEOMETRY AND MEASURESUREMENT Student Pages for Packet 6: Drawings and Constructions GEO6.1 Geometric Drawings Review geometric notation and vocabulary. Use a compass and a ruler to make
The Pythagorean Theorem is used in many careers on a regular basis. Construction
 Applying the Pythagorean Theorem Lesson 2.5 The Pythagorean Theorem is used in many careers on a regular basis. Construction workers and cabinet makers use the Pythagorean Theorem to determine lengths
Applying the Pythagorean Theorem Lesson 2.5 The Pythagorean Theorem is used in many careers on a regular basis. Construction workers and cabinet makers use the Pythagorean Theorem to determine lengths
1. What term describes a transformation that does not change a figure s size or shape?
 1. What term describes a transformation that does not change a figure s size or shape? () similarity () isometry () collinearity (D) symmetry For questions 2 4, use the diagram showing parallelogram D.
1. What term describes a transformation that does not change a figure s size or shape? () similarity () isometry () collinearity (D) symmetry For questions 2 4, use the diagram showing parallelogram D.
3. Given the similarity transformation shown below; identify the composition:
 Midterm Multiple Choice Practice 1. Based on the construction below, which statement must be true? 1 1) m ABD m CBD 2 2) m ABD m CBD 3) m ABD m ABC 1 4) m CBD m ABD 2 2. Line segment AB is shown in the
Midterm Multiple Choice Practice 1. Based on the construction below, which statement must be true? 1 1) m ABD m CBD 2 2) m ABD m CBD 3) m ABD m ABC 1 4) m CBD m ABD 2 2. Line segment AB is shown in the
What You ll Learn. Why It s Important
 Many artists use geometric concepts in their work. Think about what you have learned in geometry. How do these examples of First Nations art and architecture show geometry ideas? What You ll Learn Identify
Many artists use geometric concepts in their work. Think about what you have learned in geometry. How do these examples of First Nations art and architecture show geometry ideas? What You ll Learn Identify
Name. Ms. Nong. Due on: Per: Geometry 2 nd semester Math packet # 2 Standards: 8.0 and 16.0
 Name FRIDAY, FEBRUARY 24 Due on: Per: TH Geometry 2 nd semester Math packet # 2 Standards: 8.0 and 16.0 8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume
Name FRIDAY, FEBRUARY 24 Due on: Per: TH Geometry 2 nd semester Math packet # 2 Standards: 8.0 and 16.0 8.0 Students know, derive, and solve problems involving the perimeter, circumference, area, volume
2. Here are some triangles. (a) Write down the letter of the triangle that is. right-angled, ... (ii) isosceles. ... (2)
 Topic 8 Shapes 2. Here are some triangles. A B C D F E G (a) Write down the letter of the triangle that is (i) right-angled,... (ii) isosceles.... (2) Two of the triangles are congruent. (b) Write down
Topic 8 Shapes 2. Here are some triangles. A B C D F E G (a) Write down the letter of the triangle that is (i) right-angled,... (ii) isosceles.... (2) Two of the triangles are congruent. (b) Write down
Similar Figures 2.5. ACTIVITY: Reducing Photographs. How can you use proportions to help make decisions in art, design, and magazine layouts?
 .5 Similar Figures How can you use proportions to help make decisions in art, design, and magazine layouts? In a computer art program, when you click and drag on a side of a photograph, you distort it.
.5 Similar Figures How can you use proportions to help make decisions in art, design, and magazine layouts? In a computer art program, when you click and drag on a side of a photograph, you distort it.
UNIT 10 PERIMETER AND AREA
 UNIT 10 PERIMETER AND AREA INTRODUCTION In this Unit, we will define basic geometric shapes and use definitions to categorize geometric figures. Then we will use the ideas of measuring length and area
UNIT 10 PERIMETER AND AREA INTRODUCTION In this Unit, we will define basic geometric shapes and use definitions to categorize geometric figures. Then we will use the ideas of measuring length and area
STRAND H: Angle Geometry
 Mathematics SKE, Strand H UNIT H3 onstructions and Loci: Text STRND H: ngle Geometry H3 onstructions and Loci Text ontents Section H3.1 Drawing and Symmetry H3.2 onstructing Triangles and ther Shapes H3.3
Mathematics SKE, Strand H UNIT H3 onstructions and Loci: Text STRND H: ngle Geometry H3 onstructions and Loci Text ontents Section H3.1 Drawing and Symmetry H3.2 onstructing Triangles and ther Shapes H3.3
Name: Date: Chapter 2 Quiz Geometry. Multiple Choice Identify the choice that best completes the statement or answers the question.
 Name: Date: Chapter 2 Quiz Geometry Multiple Choice Identify the choice that best completes the statement or answers the question. 1. What is the value of x? Identify the missing justifications.,, and.
Name: Date: Chapter 2 Quiz Geometry Multiple Choice Identify the choice that best completes the statement or answers the question. 1. What is the value of x? Identify the missing justifications.,, and.
The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY. Wednesday, January 29, :15 a.m. to 12:15 p.m.
 GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
GEOMETRY The University of the State of New York REGENTS HIGH SCHOOL EXAMINATION GEOMETRY Wednesday, January 29, 2014 9:15 a.m. to 12:15 p.m., only Student Name: School Name: The possession or use of any
1. Reasoning If the question for part (b) asked for the locus of points in a plane 1 cm from < AB >, how would the sketch change?
 12-6 Locus: Set of Points ommon ore State Standards G-GMD..4... Identify three-dimensional objects generated by rotations of two-dimensional objects. MP 1, MP 3, MP 4, MP 6 Objective To draw and describe
12-6 Locus: Set of Points ommon ore State Standards G-GMD..4... Identify three-dimensional objects generated by rotations of two-dimensional objects. MP 1, MP 3, MP 4, MP 6 Objective To draw and describe
Geometry Tutor Worksheet 9 Quadrilaterals
 Geometry Tutor Worksheet 9 Quadrilaterals 1 Geometry Tutor - Worksheet 9 - Quadrilaterals 1. Which name best describes quadrilateral DEFG? 2. Which name best describes quadrilateral ABCD? 3. Which name
Geometry Tutor Worksheet 9 Quadrilaterals 1 Geometry Tutor - Worksheet 9 - Quadrilaterals 1. Which name best describes quadrilateral DEFG? 2. Which name best describes quadrilateral ABCD? 3. Which name
Parallels and Euclidean Geometry
 Parallels and Euclidean Geometry Lines l and m which are coplanar but do not meet are said to be parallel; we denote this by writing l m. Likewise, segments or rays are parallel if they are subsets of
Parallels and Euclidean Geometry Lines l and m which are coplanar but do not meet are said to be parallel; we denote this by writing l m. Likewise, segments or rays are parallel if they are subsets of
The Grade 6 Common Core State Standards for Geometry specify that students should
 The focus for students in geometry at this level is reasoning about area, surface area, and volume. Students also learn to work with visual tools for representing shapes, such as graphs in the coordinate
The focus for students in geometry at this level is reasoning about area, surface area, and volume. Students also learn to work with visual tools for representing shapes, such as graphs in the coordinate
6-3 Conditions for Parallelograms
 Warm Up Justify each statement. 1. 2. Reflex Prop. of Conv. of Alt. Int. s Thm. Evaluate each expression for x = 12 and y = 8.5. 3. 2x + 7 4. 16x 9 31 183 5. (8y + 5) 73 Objective Prove that a given quadrilateral
Warm Up Justify each statement. 1. 2. Reflex Prop. of Conv. of Alt. Int. s Thm. Evaluate each expression for x = 12 and y = 8.5. 3. 2x + 7 4. 16x 9 31 183 5. (8y + 5) 73 Objective Prove that a given quadrilateral
Elizabeth City State University Elizabeth City, North Carolina27909 STATE REGIONAL MATHEMATICS CONTEST COMPREHENSIVE TEST BOOKLET
 Elizabeth City State University Elizabeth City, North Carolina27909 2014 STATE REGIONAL MATHEMATICS CONTEST COMPREHENSIVE TEST BOOKLET Directions: Each problem in this test is followed by five suggested
Elizabeth City State University Elizabeth City, North Carolina27909 2014 STATE REGIONAL MATHEMATICS CONTEST COMPREHENSIVE TEST BOOKLET Directions: Each problem in this test is followed by five suggested
Assignment Assigned Date Due Date Grade 4.7 Worksheet
 Geometry Unit 4 and 5: Packet 2 QUADRILATERALS This is a packet containing the homework and some classwork for the first half of the first unit of geometry. This MUST be completed and turned in before
Geometry Unit 4 and 5: Packet 2 QUADRILATERALS This is a packet containing the homework and some classwork for the first half of the first unit of geometry. This MUST be completed and turned in before
AW Math 10 UNIT 6 SIMILARITY OF FIGURES
 AW Math 10 UNIT 6 SIMILARITY OF FIGURES Assignment Title Work to complete Complete 1 Review Proportional Reasoning Cross Multiply and Divide 2 Similar Figures Similar Figures 3 4 Determining Sides in Similar
AW Math 10 UNIT 6 SIMILARITY OF FIGURES Assignment Title Work to complete Complete 1 Review Proportional Reasoning Cross Multiply and Divide 2 Similar Figures Similar Figures 3 4 Determining Sides in Similar
