Unit 7 Partial Derivatives and Optimization
|
|
|
- Annabella Blankenship
- 5 years ago
- Views:
Transcription
1 Unit 7 Partial Derivatives and Optimization We have learned some important applications of the ordinary derivative in finding maxima and minima. We now move on to a topic called partial derivatives which may be used to find local maxima and minima of surfaces ( functions of two variables). Definition 7.1. Given some function y = f(x) thenwehavetwowaysof interpreting the derivative dy dx (1) Intuitively, dy measures the rate of change of the variable y with respect dx to the variable x (2) Geometrically, dy can be interpreted as the equation for the slope of the dx tangent line to the curve y = f(x). Similarily, if we have z = f(x, y), a function of two variables we can define what is called a partial derivative: f x = z x and f y = z y :ThePartial derivative of z with respect to x. :ThePartial derivative of z with respect to y. Partial derivatives ( or simply partials ) can be interpreted geometrically as well as intuitively. More on that later, now let s learn how to calculate partials. To calculate f we simply treat y as if it were a constant and then take x the usual derivative of f(x,y) with respect to x. Similarily, to calculate f we y simply treat x as if it were a constant and then take the usual derivative of f(x,y) with respect to y. Recalling that x and y are just dummy variables, the generalization of this process is transparent. 1
2 Example 1. Given the function z =2xy 3 +3x 2 +2y 3, calculate each of its partials. Solution: To find z we treat y as if it were a constant and then differentiate x so: x (2xy3 +3x 2 +2y 3 )=2y 3 +6x +0=2y 3 +6x To find z we treat x as if it were a constant and then differentiate ( with y respect to y) so: y (2xy3 +3x 2 +2y 3 )=2x(3y 2 )+0+6y 2 =6xy 2 +6y 2 =6y 2 (x +1) Example 2. given the function f(x, y, z) =e xy + xyz, calculate each of its partials. Solution: To find f x differentiate so: x (exy + xyz) =e xy ( x (xy)) + yz = exy y + yz Similarily, in finding f y we treat y and z as if they were constant and then we treat x and z as if they were constant and then differentiate ( with respect to y) so: y (exy + xyz) =e xy ( y (xy)) + xz = exy x + xz And, in finding f we treat x and y as if they were constant and then differentiate ( with respect to z) so: z z (exy + xyz) =e xy ( z (xy)) + xy = exy (0) + xz = xz Along with these new definitions comes some new notation which parallels that used for functions of single variables: Functions of one variable, say f(x) Functions of 2variables, say f(x,y) f (x) or df dx f x or f x or f x (x, y) f (a) or ( df dx )] x=a ( f x )] x=a or f x (a, y) ( f x )] x=a,y=b or f x (a, b) 2
3 The following example is very important, it illustrates and adds to the previous points and should be read carefully. Example 3. Suppose f(x, y) =x 2 y + xe xy + x3 4, find (a) f y (b)f x (x, 0) (c)f x (0, 1) (d)f y (1, 1) Solution: (a) To calculate f y we simply hold x as constant and differentiate with respect to y: f y = y (x2 y + xe xy + x3 4 ) = 2xy + xe xy y (xy)+ y (x3 4 ) = 2xy + xe xy (x)+0 = 2xy + x 2 e xy So we have f y =2xy + x 2 e xy (b) To calculate f x (x, 0) we must hold y constant and since we are going to plug in y = 0 in the result (we are asked to find the partial at (x, 0))we might as well plug in y = 0 initially, as this will yield calculations simpler to make. This can be done in general, in fact we say formally that f x (x, a) = f(x, a) x Using this fact we have: f x (x, 0) = f(x, 0) x = x (x0 + x 2 e 0 + x3 4 ) = x (1 + x2 + x3 4 ) = 2x x2 3
4 So we have f x (x, 0) = 2x x2 (c) To calculate f x (0, 1) we use the same argument as in (b) to see that With this in mind we have f x (a, b) = x f(x, b)] x=a f x (0, 1) = x f(x, 1)] x=0 = x (x2 + xe x + x3 4 )] x=0 = (2x + e x + xe x x2 )] x=0 = 1 So we have f x (0, 1) = 1 (d)to calculate f y (1, 1) we use once again the argument in (b) to see that With this in mind we have f y (a, b) = y f(a, y)] y=b f y (1, 1) = y f(1,y)] y=1 = x (y + ey )] y=1 = (1+e y +0)] y=1 = 1+e So we have f y (1, 1) = 1 + e. This example leads us naturally to the next topic. 4
5 Interpreting Partials at a Specific Point Intuitive interpretation: We may interpret a partial derivative as a rate of change. For example suppose we have a function f(x, y) andf x (2, 3) = 10 and f y (2, 3) = 2. This can then be interpreted as saying that at the point (2,3), a unit increase in x will result in an approximate increase of 10 units in the function, f, whereas a unit increase in y at the same point will result in an approximate increase of only 2units for the function, f. Geometric Interpretation: As with the ordinary derivative, partial derivatives can be interpreted as slopes of tangent lines. The partial derivative of a function f(x, y) with respect to x at the point where (x, y) =(a, b) (i.e. at the point (a,b,f(a,b)) on the surface) for example, (see diagram) will be the slope of the tangent line to the curve obtained by holding y constant at b, at x = a. We are in effect intersecting the surface z = f(x,y) with the plane y = b which is a curve, and then finding the slope of the usual tangent line at the point where x = a. Figure 1: The Geometric Interpretation of Partials Both of the above interpretations have their use, the intuitive is the easiest to see in applications whereas the geometric interpretation often provides the reasoning behind results. 5
6 Example 4. Suppose p = f(l, K) =90L 2 3 K 1 3 is the production function for a certain manufacturing process where: P = the number of units produced L = the number of units of labour used K = the number of units of capital required Calculate P L (8, 27) and P K (8, 27) note: P L andp K are known as marginal productivity of labour and marginal productivity of capital respectively. Solution: As with the previous examples we have: P L (L, K) =60L 1 3 K 1 3 and P K (L, K) =30L 2 3 K 2 3 therefore P L (8, 27) = (60) = 90, andp K (8, 27) = (30) Interpretation: If labour and capital are currently at 8 and 27 respectively, then an increase in labour of one unit ( from 8 to 9 ) will result in an approximate increase in production of 90 units. An increase in capital however, from 27 to 28 units will result in an approximate increase in production of only 13.3 units. Higher Order Partial Derivatives Definition 7.2. As we did with the ordinary derivative, we now define higher order partials. There are no surprizes here as far as the mechanics of the processes are concerned. We define the: Second partial of f with respect to x as: 2 f = ( f ) or f x 2 x x xx =(f x ) x Second partial of f with respect to y as: 2 f = ( f ) or f y 2 y y yy =(f y ) y Mixed partials of f as: 2 f = ( f ) or f xy x y xy =(f x ) y and 2 f = ( f ) or f yx y x yx =(f y ) x The third, fourth, and n th partials are defined in the natural way. One surprizing fact is the following. Theorem 7.3. For any continuous function f(x, y), f xy = f yx So we may take mixed partials in any order we please as long as our function is continuous. As almost every function encountered in this course is continuous this is a very handy theorem. 6
7 Example 5. Suppose f(x, y) =x 2 y 3 + ye y, find (a) f xx (b) f yy (c) f yx (d) f xy Solution: (a) f xx = x (f x ) = x (2xy3 +0) = 2y 3 (b)f yy = y (f y ) = y (3x2 y 2 + e y + ye y ) = 6x 2 y + e y + e y + ye y ) = 6x 2 y + e y (2+ y) (c)f xy = y (f x ) = y (2xy3 ) = 6xy 3 (d)f yx = f xy since f is continuous = 6xy 3 by(c) Optimization Just as with the ordinary derivative, we may use partials to find extreme values of functions. Definition 7.4. Let D be the domain of a function f(x, y) and(a, b) D. Then we say that 7
8 (i) f(a, b) isthemaximum value of f(x, y) ond if f(a, b) f(x, y) for every (x, y) D (ii)f(a, b) istheminimum value of f(x, y) ond if f(a, b) f(x, y) for every (x, y) D If the inequalities above hold in some neighbourhood of (a, b) then the above definitions become those for local maximum and local minimum values. Example 6. Figure 2shows part of the surface f(x, y) =x 2 + y 2 which is easily seen to have both a local minimum and a minimum value ( of 0 ) at the point (0, 0). Figure 2: f(x, y) =x 2 + y 2 8
9 Example 7. The following figure shows a surface which demonstrates the previous definitions. Figure 3: Maximal and Minimal Points of a Surface Definition 7.5. By an extreme value of a function, we mean a point where either a (local) maximum or a (local) minimum occurs. Definition 7.6. By a critical point of a function f, we will mean (1) A point where all partials are zero, or (2) A boundary point of the domain, or (3) A point where the graph has some type of pathalogical behaviour. For example a point where the graph is ripped or has a corner, or fluctuates wildly. 9
10 Our main concern is with condition (1) and we will not talk about condition (3) at all. We need to define critical point in this way so that we may state the following theorem. Theorem 7.7. An extreme value may only occur at a critical point. Finding Extreme Values Unlike the situation with the regular derivative, it is not enough to require that all first derivatives be zero to guarantee an extreme value. For example the saddle surface ( named for the obvious reason) shown in figure 4 will have f x =0andf y = 0 at the point P, but by observation we see that P is neither a maximum nor a minimum point of the surface. Figure 4: Saddle Surface Since there are creatures such as this lurking about in 3-space we turn to a new test to find extreme values, namely the second partials test. 10
11 Theorem 7.8. The Second Partials Test Suppose f(x, y) has continuous second partials in a neighbourhood of (a, b) and that f x (a, b) =0=f y (a, b) (so (a, b) is a critical point of f).define: then: T (a, b) =f xx (a, b)f yy (a, b) [f xy (a, b)] 2 (1) If T (a, b) > 0 and f xx (a, b) < 0 then f(a, b) is a local maximum value. (2) If T (a, b) > 0 and f xx (a, b) > 0 then f(a, b) is a local minimum value. (3) If T (a, b) < 0 then f(a, b) is a saddle point of f. (like P in fig3) (4) If T (a, b) =0then this test yields no information. Example 8. Find the local extrema of f(x, y) =x 2 +3y 2 +4x 9y +10 Solution: We shall use the second partials test so we should first find our partials: f x =2x +4,f y =9y 2 9, f xx =2, f yy =18y, f xy =0 We now set both first partials to zero to solve for our critical points: f x =0 x = 2 f y =0 y = ±1 Therefore our critical points are ( 2, 1)and( 2, 1) We now test the critical points using the second partials test: ( 2, 1) : T (a, b) =f xx (a, b)f yy (a, b) [f xy (a, b)] 2 so T ( 2, 1) = f xx ( 2, 1)f yy ( 2, 1) [f xy ( 2, 1)] 2 =36 11
12 Therefore, by the second partials test, f( 2, 1) = 0 is a local minimum. ( 2, 1) : T (a, b) =f xx (a, b)f yy (a, b) [f xy (a, b)] 2 so T ( 2, 1) = f xx ( 2, 1)f yy ( 2, 1) [f xy ( 2, 1)] 2 = 36 < 0 Therefore, by the second partials test, f( 2, 1) = 18 is a saddle point. Example 9. Determine the dimensions of an open rectangular box (with dimensions shown) with volume 32m 2, and the least (outer) surface area. Figure 5: Solution: We wish to minimize the area given by: A = xy +2xz +2yz subject to volume = xyz =32,whichistosayz = 32. Substituting into the xy area function we see that we wish to minimize: A = xy + 64 y + 64 xy 12
13 Find Critical points: A x = 0 y 64 x 2 = 0 y = 64 x 2 A y = 0 x 64 y 2 = 0 x = 64 y 2 (a) (b) Substituting (b) into (a) we get: y = 1 64 y4 y 4 64y = 0 y(y 3 64) = 0 y =4or y = 0 Substituting y=4 into (b) we get x=4, so a critical point is (4,4). The value y=0 is of no interest as it gives a flat box. So all we must do is check with the second partials test that the point (4,4) is indeed a minimum for the area function: A xx (4, 4) = =2> 0 So, A yy (4, 4) = =2 A xy (4, 4) = 0 T (4, 4) = (2)(2) 0=4> 0 Therefore, by the second partials test (4,4) is indeed a local minimum for A, and so x =4,y = 4 are the dimensions requested. 13
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables
 Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Lecture 19 - Partial Derivatives and Extrema of Functions of Two Variables 19.1 Partial Derivatives We wish to maximize functions of two variables. This will involve taking derivatives. Example: Consider
Maxima and Minima. Terminology note: Do not confuse the maximum f(a, b) (a number) with the point (a, b) where the maximum occurs.
 10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
10-11-2010 HW: 14.7: 1,5,7,13,29,33,39,51,55 Maxima and Minima In this very important chapter, we describe how to use the tools of calculus to locate the maxima and minima of a function of two variables.
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
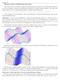 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Section 15.3 Partial Derivatives
 Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
Section 5.3 Partial Derivatives Differentiating Functions of more than one Variable. Basic Definitions In single variable calculus, the derivative is defined to be the instantaneous rate of change of a
14.4. Tangent Planes. Tangent Planes. Tangent Planes. Tangent Planes. Partial Derivatives. Tangent Planes and Linear Approximations
 14 Partial Derivatives 14.4 and Linear Approximations Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Suppose a surface S has equation z = f(x, y), where
14 Partial Derivatives 14.4 and Linear Approximations Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Suppose a surface S has equation z = f(x, y), where
Math 233. Extrema of Functions of Two Variables Basics
 Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Math 233. Extrema of Functions of Two Variables Basics Theorem (Extreme Value Theorem) Let f be a continuous function of two variables x and y defined on a closed bounded region R in the xy-plane. Then
Calculus II Fall 2014
 Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
CHAPTER 11 PARTIAL DERIVATIVES
 CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Math 32, October 22 & 27: Maxima & Minima
 Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Math 32, October 22 & 27: Maxima & Minima Section 1: Critical Points Just as in the single variable case, for multivariate functions we are often interested in determining extreme values of the function.
Review guide for midterm 2 in Math 233 March 30, 2009
 Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
11.2 LIMITS AND CONTINUITY
 11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
11. LIMITS AND CONTINUITY INTRODUCTION: Consider functions of one variable y = f(x). If you are told that f(x) is continuous at x = a, explain what the graph looks like near x = a. Formal definition of
The Chain Rule, Higher Partial Derivatives & Opti- mization
 The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
LECTURE 19 - LAGRANGE MULTIPLIERS
 LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
Solutions to the problems from Written assignment 2 Math 222 Winter 2015
 Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
Solutions to the problems from Written assignment 2 Math 222 Winter 2015 1. Determine if the following limits exist, and if a limit exists, find its value. x2 y (a) The limit of f(x, y) = x 4 as (x, y)
18.3. Stationary Points. Introduction. Prerequisites. Learning Outcomes
 Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
Stationary Points 8.3 Introduction The calculation of the optimum value of a function of two variables is a common requirement in many areas of engineering, for example in thermodynamics. Unlike the case
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
MULTI-VARIABLE OPTIMIZATION NOTES. 1. Identifying Critical Points
 MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
MULTI-VARIABLE OPTIMIZATION NOTES HARRIS MATH CAMP 2018 1. Identifying Critical Points Definition. Let f : R 2! R. Then f has a local maximum at (x 0,y 0 ) if there exists some disc D around (x 0,y 0 )
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Name: ID: Section: Math 233 Exam 2. Page 1. This exam has 17 questions:
 Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
B) 0 C) 1 D) No limit. x2 + y2 4) A) 2 B) 0 C) 1 D) No limit. A) 1 B) 2 C) 0 D) No limit. 8xy 6) A) 1 B) 0 C) π D) -1
 MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and
![[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and [f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and](/thumbs/92/108353356.jpg) Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Functions of several variables
 Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
MATH 12 CLASS 9 NOTES, OCT Contents 1. Tangent planes 1 2. Definition of differentiability 3 3. Differentials 4
 MATH 2 CLASS 9 NOTES, OCT 0 20 Contents. Tangent planes 2. Definition of differentiability 3 3. Differentials 4. Tangent planes Recall that the derivative of a single variable function can be interpreted
MATH 2 CLASS 9 NOTES, OCT 0 20 Contents. Tangent planes 2. Definition of differentiability 3 3. Differentials 4. Tangent planes Recall that the derivative of a single variable function can be interpreted
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
ANSWER KEY. (a) For each of the following partials derivatives, use the contour plot to decide whether they are positive, negative, or zero.
 Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
Math 2411 Calc III Practice Exam 2
 Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
Math 2411 Calc III Practice Exam 2 This is a practice exam. The actual exam consists of questions of the type found in this practice exam, but will be shorter. If you have questions do not hesitate to
Partial Differentiation 1 Introduction
 Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
Partial Differentiation 1 Introduction In the first part of this course you have met the idea of a derivative. To recap what this means, recall that if you have a function, z say, then the slope of the
MATH 105: Midterm #1 Practice Problems
 Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
i + u 2 j be the unit vector that has its initial point at (a, b) and points in the desired direction. It determines a line in the xy-plane:
 1 Directional Derivatives and Gradients Suppose we need to compute the rate of change of f(x, y) with respect to the distance from a point (a, b) in some direction. Let u = u 1 i + u 2 j be the unit vector
1 Directional Derivatives and Gradients Suppose we need to compute the rate of change of f(x, y) with respect to the distance from a point (a, b) in some direction. Let u = u 1 i + u 2 j be the unit vector
INTEGRATION OVER NON-RECTANGULAR REGIONS. Contents 1. A slightly more general form of Fubini s Theorem
 INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
Mock final exam Math fall 2007
 Mock final exam Math - fall 7 Fernando Guevara Vasquez December 5 7. Consider the curve r(t) = ti + tj + 5 t t k, t. (a) Show that the curve lies on a sphere centered at the origin. (b) Where does the
Mock final exam Math - fall 7 Fernando Guevara Vasquez December 5 7. Consider the curve r(t) = ti + tj + 5 t t k, t. (a) Show that the curve lies on a sphere centered at the origin. (b) Where does the
Math 5BI: Problem Set 1 Linearizing functions of several variables
 Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
MATH 8 FALL 2010 CLASS 27, 11/19/ Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits
 MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
MATH 20C: FUNDAMENTALS OF CALCULUS II FINAL EXAM
 MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
MATH 2C: FUNDAMENTALS OF CALCULUS II FINAL EXAM Name Please circle the answer to each of the following problems. You may use an approved calculator. Each multiple choice problem is worth 2 points.. Multiple
Review Problems. Calculus IIIA: page 1 of??
 Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
Review Problems The final is comprehensive exam (although the material from the last third of the course will be emphasized). You are encouraged to work carefully through this review package, and to revisit
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A
 Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
Math for Economics 1 New York University FINAL EXAM, Fall 2013 VERSION A Name: ID: Circle your instructor and lecture below: Jankowski-001 Jankowski-006 Ramakrishnan-013 Read all of the following information
MATH 234 THIRD SEMESTER CALCULUS
 MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
MATH 234 THIRD SEMESTER CALCULUS Fall 2009 1 2 Math 234 3rd Semester Calculus Lecture notes version 0.9(Fall 2009) This is a self contained set of lecture notes for Math 234. The notes were written by
Exam 2 Review Sheet. r(t) = x(t), y(t), z(t)
 Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Calculus of Several Variables
 Benjamin McKay Calculus of Several Variables Optimisation and Finance February 18, 2018 This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. Preface The course is
Benjamin McKay Calculus of Several Variables Optimisation and Finance February 18, 2018 This work is licensed under a Creative Commons Attribution-ShareAlike 3.0 Unported License. Preface The course is
MATH Exam 2 Solutions November 16, 2015
 MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Test Yourself. 11. The angle in degrees between u and w. 12. A vector parallel to v, but of length 2.
 Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Discussion 8 Solution Thursday, February 10th. Consider the function f(x, y) := y 2 x 2.
 Discussion 8 Solution Thursday, February 10th. 1. Consider the function f(x, y) := y 2 x 2. (a) This function is a mapping from R n to R m. Determine the values of n and m. The value of n is 2 corresponding
Discussion 8 Solution Thursday, February 10th. 1. Consider the function f(x, y) := y 2 x 2. (a) This function is a mapping from R n to R m. Determine the values of n and m. The value of n is 2 corresponding
Lecture 4 : Monday April 6th
 Lecture 4 : Monday April 6th jacques@ucsd.edu Key concepts : Tangent hyperplane, Gradient, Directional derivative, Level curve Know how to find equation of tangent hyperplane, gradient, directional derivatives,
Lecture 4 : Monday April 6th jacques@ucsd.edu Key concepts : Tangent hyperplane, Gradient, Directional derivative, Level curve Know how to find equation of tangent hyperplane, gradient, directional derivatives,
Instructions: Good luck! Math 21a Second Midterm Exam Spring, 2009
 Your Name Your Signature Instructions: Please begin by printing and signing your name in the boxes above and by checking your section in the box to the right You are allowed 2 hours (120 minutes) for this
Your Name Your Signature Instructions: Please begin by printing and signing your name in the boxes above and by checking your section in the box to the right You are allowed 2 hours (120 minutes) for this
Chapter 16. Partial Derivatives
 Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Review Sheet for Math 230, Midterm exam 2. Fall 2006
 Review Sheet for Math 230, Midterm exam 2. Fall 2006 October 31, 2006 The second midterm exam will take place: Monday, November 13, from 8:15 to 9:30 pm. It will cover chapter 15 and sections 16.1 16.4,
Review Sheet for Math 230, Midterm exam 2. Fall 2006 October 31, 2006 The second midterm exam will take place: Monday, November 13, from 8:15 to 9:30 pm. It will cover chapter 15 and sections 16.1 16.4,
4 to find the dimensions of the rectangle that have the maximum area. 2y A =?? f(x, y) = (2x)(2y) = 4xy
 Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
MATH Review Exam II 03/06/11
 MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
11/18/2008 SECOND HOURLY FIRST PRACTICE Math 21a, Fall Name:
 11/18/28 SECOND HOURLY FIRST PRACTICE Math 21a, Fall 28 Name: MWF 9 Chung-Jun John Tsai MWF 1 Ivana Bozic MWF 1 Peter Garfield MWF 1 Oliver Knill MWF 11 Peter Garfield MWF 11 Stefan Hornet MWF 12 Aleksander
11/18/28 SECOND HOURLY FIRST PRACTICE Math 21a, Fall 28 Name: MWF 9 Chung-Jun John Tsai MWF 1 Ivana Bozic MWF 1 Peter Garfield MWF 1 Oliver Knill MWF 11 Peter Garfield MWF 11 Stefan Hornet MWF 12 Aleksander
Maxima and Minima. Chapter Local and Global extrema. 5.2 Continuous functions on closed and bounded sets Definition of global extrema
 Chapter 5 Maxima and Minima In first semester calculus we learned how to find the maximal and minimal values of a function y = f(x) of one variable. The basic method is as follows: assuming the independent
Chapter 5 Maxima and Minima In first semester calculus we learned how to find the maximal and minimal values of a function y = f(x) of one variable. The basic method is as follows: assuming the independent
Review #Final Exam MATH 142-Drost
 Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
Fall 2007 1 Review #Final Exam MATH 142-Drost 1. Find the domain of the function f(x) = x 1 x 2 if x3 2. Suppose 450 items are sold per day at a price of $53 per item and that 650 items are
Calculus 3 Exam 2 31 October 2017
 Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Calculus 3 Exam 2 31 October 2017 Name: Instructions: Be sure to read each problem s directions. Write clearly during the exam and fully erase or mark out anything you do not want graded. You may use your
Lecture 15. Global extrema and Lagrange multipliers. Dan Nichols MATH 233, Spring 2018 University of Massachusetts
 Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Chapter 2: Functions and Graphs Lesson Index & Summary
 Section 1: Relations and Graphs Cartesian coordinates Screen 2 Coordinate plane Screen 2 Domain of relation Screen 3 Graph of a relation Screen 3 Linear equation Screen 6 Ordered pairs Screen 1 Origin
Section 1: Relations and Graphs Cartesian coordinates Screen 2 Coordinate plane Screen 2 Domain of relation Screen 3 Graph of a relation Screen 3 Linear equation Screen 6 Ordered pairs Screen 1 Origin
I II III IV V VI VII VIII IX X Total
 1 of 16 HAND IN Answers recorded on exam paper. DEPARTMENT OF MATHEMATICS AND STATISTICS QUEEN S UNIVERSITY AT KINGSTON MATH 121/124 - APR 2018 Section 700 - CDS Students ONLY Instructor: A. Ableson INSTRUCTIONS:
1 of 16 HAND IN Answers recorded on exam paper. DEPARTMENT OF MATHEMATICS AND STATISTICS QUEEN S UNIVERSITY AT KINGSTON MATH 121/124 - APR 2018 Section 700 - CDS Students ONLY Instructor: A. Ableson INSTRUCTIONS:
14.2 Limits and Continuity
 14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
14 Partial Derivatives 14.2 Copyright Cengage Learning. All rights reserved. Copyright Cengage Learning. All rights reserved. Let s compare the behavior of the functions Tables 1 2 show values of f(x,
1. Vector Fields. f 1 (x, y, z)i + f 2 (x, y, z)j + f 3 (x, y, z)k.
 HAPTER 14 Vector alculus 1. Vector Fields Definition. A vector field in the plane is a function F(x, y) from R into V, We write F(x, y) = hf 1 (x, y), f (x, y)i = f 1 (x, y)i + f (x, y)j. A vector field
HAPTER 14 Vector alculus 1. Vector Fields Definition. A vector field in the plane is a function F(x, y) from R into V, We write F(x, y) = hf 1 (x, y), f (x, y)i = f 1 (x, y)i + f (x, y)j. A vector field
1. Let f(x, y) = 4x 2 4xy + 4y 2, and suppose x = cos t and y = sin t. Find df dt using the chain rule.
 Math 234 WES WORKSHEET 9 Spring 2015 1. Let f(x, y) = 4x 2 4xy + 4y 2, and suppose x = cos t and y = sin t. Find df dt using the chain rule. 2. Let f(x, y) = x 2 + y 2. Find all the points on the level
Math 234 WES WORKSHEET 9 Spring 2015 1. Let f(x, y) = 4x 2 4xy + 4y 2, and suppose x = cos t and y = sin t. Find df dt using the chain rule. 2. Let f(x, y) = x 2 + y 2. Find all the points on the level
Independence of Path and Conservative Vector Fields
 Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Differentiable functions (Sec. 14.4)
 Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
REVIEW SHEET FOR MIDTERM 2: ADVANCED
 REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
MATH 261 EXAM II PRACTICE PROBLEMS
 MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
MATH 61 EXAM II PRACTICE PROBLEMS These practice problems are pulled from actual midterms in previous semesters. Exam typically has 6 problems on it, with no more than one problem of any given type (e.g.,
3. (12 %) Find an equation of the tangent plane at the point (2,2,1) to the surface. u = t. Find z t. v = se t.
 EXAM - Math 17 NAME: I.D.: Instrction: Circle yor answers and show all yor work clearly. Messing arond may reslt in losing credits, since the grader may be forced to pick the worst to grade. Soltions with
EXAM - Math 17 NAME: I.D.: Instrction: Circle yor answers and show all yor work clearly. Messing arond may reslt in losing credits, since the grader may be forced to pick the worst to grade. Soltions with
Double Integrals over More General Regions
 Jim Lambers MAT 8 Spring Semester 9-1 Lecture 11 Notes These notes correspond to Section 1. in Stewart and Sections 5.3 and 5.4 in Marsden and Tromba. ouble Integrals over More General Regions We have
Jim Lambers MAT 8 Spring Semester 9-1 Lecture 11 Notes These notes correspond to Section 1. in Stewart and Sections 5.3 and 5.4 in Marsden and Tromba. ouble Integrals over More General Regions We have
Chapter 9 Linear equations/graphing. 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane
 Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
Chapter 9 Linear equations/graphing 1) Be able to graph points on coordinate plane 2) Determine the quadrant for a point on coordinate plane Rectangular Coordinate System Quadrant II (-,+) y-axis Quadrant
WESI 205 Workbook. 1 Review. 2 Graphing in 3D
 1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers
 SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
SYDE 112, LECTURE 34 & 35: Optimization on Restricted Domains and Lagrange Multipliers 1 Restricted Domains If we are asked to determine the maximal and minimal values of an arbitrary multivariable function
Level Curves, Partial Derivatives
 Unit #18 : Level Curves, Partial Derivatives Goals: To learn how to use and interpret contour diagrams as a way of visualizing functions of two variables. To study linear functions of two variables. To
Unit #18 : Level Curves, Partial Derivatives Goals: To learn how to use and interpret contour diagrams as a way of visualizing functions of two variables. To study linear functions of two variables. To
MATH 259 FINAL EXAM. Friday, May 8, Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E
 MATH 259 FINAL EXAM 1 Friday, May 8, 2009. NAME: Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E Instructions: 1. Do not separate the pages of the exam.
MATH 259 FINAL EXAM 1 Friday, May 8, 2009. NAME: Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E Instructions: 1. Do not separate the pages of the exam.
14.7 Maximum and Minimum Values
 CHAPTER 14. PARTIAL DERIVATIVES 115 14.7 Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at
CHAPTER 14. PARTIAL DERIVATIVES 115 14.7 Maximum and Minimum Values Definition. Let f(x, y) be a function. f has a local max at (a, b) iff(a, b) (a, b). f(x, y) for all (x, y) near f has a local min at
266&deployment= &UserPass=b3733cde68af274d036da170749a68f6
 Sections 14.6 and 14.7 (1482266) Question 12345678910111213141516171819202122 Due: Thu Oct 21 2010 11:59 PM PDT 1. Question DetailsSCalcET6 14.6.012. [1289020] Find the directional derivative, D u f, of
Sections 14.6 and 14.7 (1482266) Question 12345678910111213141516171819202122 Due: Thu Oct 21 2010 11:59 PM PDT 1. Question DetailsSCalcET6 14.6.012. [1289020] Find the directional derivative, D u f, of
SOLUTIONS 2. PRACTICE EXAM 2. HOURLY. Problem 1) TF questions (20 points) Circle the correct letter. No justifications are needed.
 SOLUIONS 2. PRACICE EXAM 2. HOURLY Math 21a, S03 Problem 1) questions (20 points) Circle the correct letter. No justifications are needed. A function f(x, y) on the plane for which the absolute minimum
SOLUIONS 2. PRACICE EXAM 2. HOURLY Math 21a, S03 Problem 1) questions (20 points) Circle the correct letter. No justifications are needed. A function f(x, y) on the plane for which the absolute minimum
EXERCISES CHAPTER 11. z = f(x, y) = A x α 1. x y ; (3) z = x2 + 4x + 2y. Graph the domain of the function and isoquants for z = 1 and z = 2.
 EXERCISES CHAPTER 11 1. (a) Given is a Cobb-Douglas function f : R 2 + R with z = f(x, y) = A x α 1 1 x α 2 2, where A = 1, α 1 = 1/2 and α 2 = 1/2. Graph isoquants for z = 1 and z = 2 and illustrate the
EXERCISES CHAPTER 11 1. (a) Given is a Cobb-Douglas function f : R 2 + R with z = f(x, y) = A x α 1 1 x α 2 2, where A = 1, α 1 = 1/2 and α 2 = 1/2. Graph isoquants for z = 1 and z = 2 and illustrate the
Final Exam Review Problems. P 1. Find the critical points of f(x, y) = x 2 y + 2y 2 8xy + 11 and classify them.
 Final Exam Review Problems P 1. Find the critical points of f(x, y) = x 2 y + 2y 2 8xy + 11 and classify them. 1 P 2. Find the volume of the solid bounded by the cylinder x 2 + y 2 = 9 and the planes z
Final Exam Review Problems P 1. Find the critical points of f(x, y) = x 2 y + 2y 2 8xy + 11 and classify them. 1 P 2. Find the volume of the solid bounded by the cylinder x 2 + y 2 = 9 and the planes z
Math 259 Winter Recitation Handout 9: Lagrange Multipliers
 Math 259 Winter 2009 Recitation Handout 9: Lagrange Multipliers The method of Lagrange Multipliers is an excellent technique for finding the global maximum and global minimum values of a function f(x,
Math 259 Winter 2009 Recitation Handout 9: Lagrange Multipliers The method of Lagrange Multipliers is an excellent technique for finding the global maximum and global minimum values of a function f(x,
33. Riemann Summation over Rectangular Regions
 . iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
. iemann Summation over ectangular egions A rectangular region in the xy-plane can be defined using compound inequalities, where x and y are each bound by constants such that a x a and b y b. Let z = f(x,
Practice Problems: Calculus in Polar Coordinates
 Practice Problems: Calculus in Polar Coordinates Answers. For these problems, I want to convert from polar form parametrized Cartesian form, then differentiate and take the ratio y over x to get the slope,
Practice Problems: Calculus in Polar Coordinates Answers. For these problems, I want to convert from polar form parametrized Cartesian form, then differentiate and take the ratio y over x to get the slope,
MATH 253 Page 1 of 7 Student-No.: Midterm 2 November 16, 2016 Duration: 50 minutes This test has 4 questions on 7 pages, for a total of 40 points.
 MATH 253 Page 1 of 7 Student-No.: Midterm 2 November 16, 2016 Duration: 50 minutes This test has 4 questions on 7 pages, for a total of 40 points. Read all the questions carefully before starting to work.
MATH 253 Page 1 of 7 Student-No.: Midterm 2 November 16, 2016 Duration: 50 minutes This test has 4 questions on 7 pages, for a total of 40 points. Read all the questions carefully before starting to work.
14.6 Directional Derivatives
 CHAPTER 14. PARTIAL DERIVATIVES 107 14.6 Directional Derivatives Comments. Recall that the partial derivatives can be interpreted as the derivatives along traces of f(x, y). We can reinterpret this in
CHAPTER 14. PARTIAL DERIVATIVES 107 14.6 Directional Derivatives Comments. Recall that the partial derivatives can be interpreted as the derivatives along traces of f(x, y). We can reinterpret this in
This exam contains 9 problems. CHECK THAT YOU HAVE A COMPLETE EXAM.
 Math 126 Final Examination Winter 2012 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name This exam contains 9 problems. CHECK THAT YOU HAVE A COMPLETE EXAM. This exam is closed
Math 126 Final Examination Winter 2012 Your Name Your Signature Student ID # Quiz Section Professor s Name TA s Name This exam contains 9 problems. CHECK THAT YOU HAVE A COMPLETE EXAM. This exam is closed
Math Final Exam - 6/13/2013
 Math - Final Exam - 6/13/13 NAME: SECTION: Directions: For the free response section, you must show all work. Answers without proper justification will not receive full credit. Partial credit will be awarded
Math - Final Exam - 6/13/13 NAME: SECTION: Directions: For the free response section, you must show all work. Answers without proper justification will not receive full credit. Partial credit will be awarded
 There is another online survey for those of you (freshman) who took the ALEKS placement test before the semester. Please follow the link at the Math 165 web-page, or just go to: https://illinois.edu/sb/sec/2457922
There is another online survey for those of you (freshman) who took the ALEKS placement test before the semester. Please follow the link at the Math 165 web-page, or just go to: https://illinois.edu/sb/sec/2457922
Independent of path Green s Theorem Surface Integrals. MATH203 Calculus. Dr. Bandar Al-Mohsin. School of Mathematics, KSU 20/4/14
 School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
Goals: To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition).
 Unit #23 : Lagrange Multipliers Goals: To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition). Constrained Optimization - Examples
Unit #23 : Lagrange Multipliers Goals: To study constrained optimization; that is, the maximizing or minimizing of a function subject to a constraint (or side condition). Constrained Optimization - Examples
Conic and Quadric Surface Lab page 4. NORTHEASTERN UNIVERSITY Department of Mathematics Fall 03 Conic Sections and Quadratic Surface Lab
 Conic and Quadric Surface Lab page 4 NORTHEASTERN UNIVERSITY Department of Mathematics Fall 03 Conic Sections and Quadratic Surface Lab Goals By the end of this lab you should: 1.) Be familar with the
Conic and Quadric Surface Lab page 4 NORTHEASTERN UNIVERSITY Department of Mathematics Fall 03 Conic Sections and Quadratic Surface Lab Goals By the end of this lab you should: 1.) Be familar with the
4.4 Equations of Parallel and Perpendicular
 www.ck12.org Chapter 4. Determining Linear Equations 4.4 Equations of Parallel and Perpendicular Lines Learning Objectives Determine whether lines are parallel or perpendicular. Write equations of perpendicular
www.ck12.org Chapter 4. Determining Linear Equations 4.4 Equations of Parallel and Perpendicular Lines Learning Objectives Determine whether lines are parallel or perpendicular. Write equations of perpendicular
3.5 Marginal Distributions
 STAT 421 Lecture Notes 52 3.5 Marginal Distributions Definition 3.5.1 Suppose that X and Y have a joint distribution. The c.d.f. of X derived by integrating (or summing) over the support of Y is called
STAT 421 Lecture Notes 52 3.5 Marginal Distributions Definition 3.5.1 Suppose that X and Y have a joint distribution. The c.d.f. of X derived by integrating (or summing) over the support of Y is called
DIFFERENTIAL EQUATIONS. A principal model of physical phenomena.
 DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The ordinary differential equation: The initial value: y = f(x, y) y(x 0 )=Y 0 Find a solution Y (x) onsomeintervalx 0 x b. Together these
DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The ordinary differential equation: The initial value: y = f(x, y) y(x 0 )=Y 0 Find a solution Y (x) onsomeintervalx 0 x b. Together these
Lecture 19. Vector fields. Dan Nichols MATH 233, Spring 2018 University of Massachusetts. April 10, 2018.
 Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
7/26/2018 SECOND HOURLY PRACTICE I Maths 21a, O.Knill, Summer Name:
 7/26/218 SECOND HOURLY PRACTICE I Maths 21a, O.Knill, Summer 218 Name: Start by printing your name in the above box. Try to answer each question on the same page as the question is asked. If needed, use
7/26/218 SECOND HOURLY PRACTICE I Maths 21a, O.Knill, Summer 218 Name: Start by printing your name in the above box. Try to answer each question on the same page as the question is asked. If needed, use
March 13, 2009 CHAPTER 3: PARTIAL DERIVATIVES AND DIFFERENTIATION
 March 13, 2009 CHAPTER 3: PARTIAL DERIVATIVES AND DIFFERENTIATION 1. Parial Derivaives and Differeniable funcions In all his chaper, D will denoe an open subse of R n. Definiion 1.1. Consider a funcion
March 13, 2009 CHAPTER 3: PARTIAL DERIVATIVES AND DIFFERENTIATION 1. Parial Derivaives and Differeniable funcions In all his chaper, D will denoe an open subse of R n. Definiion 1.1. Consider a funcion
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives
 ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives So far we have dealt with functions of the form y = f(x),
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives So far we have dealt with functions of the form y = f(x),
DIFFERENTIAL EQUATIONS. A principal model of physical phenomena.
 DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The equation: The initial value: y = f(x, y) y(x 0 ) = Y 0 Find solution Y (x) on some interval x 0 x b. Together these two conditions constitute
DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The equation: The initial value: y = f(x, y) y(x 0 ) = Y 0 Find solution Y (x) on some interval x 0 x b. Together these two conditions constitute
Multivariate Calculus
 Multivariate Calculus Partial Derivatives 1 Theory Recall the definition of the partial derivatives of a function of two variables, z = f(x, y): f x = lim f(x + x, y) f(x, y) x 0 x f y f(x, y + y) f(x,
Multivariate Calculus Partial Derivatives 1 Theory Recall the definition of the partial derivatives of a function of two variables, z = f(x, y): f x = lim f(x + x, y) f(x, y) x 0 x f y f(x, y + y) f(x,
