Section 8.1. Sequences and Series
|
|
|
- Raymond Bradley
- 5 years ago
- Views:
Transcription
1 Section 8.1 Sequences and Series
2 Sequences
3 Definition A sequence is a list of numbers.
4 Definition A sequence is a list of numbers. A sequence could be finite, such as: 1, 2, 3, 4
5 Definition A sequence is a list of numbers. A sequence could be finite, such as: 1, 2, 3, 4 A sequence can also be infinite, such as: 2, 4, 8, 16, 32, 64,... Here the... just means that the pattern continues forever.
6 Sequence Notation A series can also be thought of as a function where you only plug in natural numbers.
7 Sequence Notation A series can also be thought of as a function where you only plug in natural numbers. For example, 2, 4, 8, 16, 32, 64,... can be thought of as a(n) = 2 n since a(1) = 2 1 = 2, a(2) = 2 2 = 4, a(3) = 2 3 = 8, etc
8 Sequence Notation A series can also be thought of as a function where you only plug in natural numbers. For example, 2, 4, 8, 16, 32, 64,... can be thought of as a(n) = 2 n since a(1) = 2 1 = 2, a(2) = 2 2 = 4, a(3) = 2 3 = 8, etc Normally, however, the sequence is written with the input variable as a subscript: a n = 2 n Here a 1 = 2, a 2 = 4, a 3 = 8, etc
9 Examples 1. Find the first three terms of the sequence a n = n+1 n.
10 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = 4 3
11 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = Find the first four terms of the sequence a n = ( 1) n n 3
12 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = Find the first four terms of the sequence a n = ( 1) n n 3 a 1 = 1, a 2 = 8, a 3 = 27, a 4 = 64
13 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = Find the first four terms of the sequence a n = ( 1) n n 3 a 1 = 1, a 2 = 8, a 3 = 27, a 4 = Find the formula for the general term a n of the sequence 2, 4, 6, 8, 10,...
14 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = Find the first four terms of the sequence a n = ( 1) n n 3 a 1 = 1, a 2 = 8, a 3 = 27, a 4 = Find the formula for the general term a n of the sequence 2, 4, 6, 8, 10,... a n = 2n
15 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = Find the first four terms of the sequence a n = ( 1) n n 3 a 1 = 1, a 2 = 8, a 3 = 27, a 4 = Find the formula for the general term a n of the sequence 2, 4, 6, 8, 10,... a n = 2n 4. Find the formula for the general term a n of the sequence 2, 6, 18, 54, 162,...
16 Examples 1. Find the first three terms of the sequence a n = n+1 n. a 1 = 2, a 2 = 3 2, a 3 = Find the first four terms of the sequence a n = ( 1) n n 3 a 1 = 1, a 2 = 8, a 3 = 27, a 4 = Find the formula for the general term a n of the sequence 2, 4, 6, 8, 10,... a n = 2n 4. Find the formula for the general term a n of the sequence 2, 6, 18, 54, 162,... a n = ( 1) n 2 3 n 1
17 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms.
18 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,...
19 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers:
20 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1
21 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1 a 4 = = 2
22 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1 a 4 = = 2 a 5 = = 3
23 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1 a 4 = = 2 a 5 = = 3 a 6 = = 5
24 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1 a 4 = = 2 a 5 = = 3 a 6 = = 5 a 7 = = 8
25 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1 a 4 = = 2 a 5 = = 3 a 6 = = 5 a 7 = = 8 a 8 = = 13
26 Recursive Sequences Some sequences can be written recursively, i.e. the terms are calculated from previous terms. The most famous example of this type of sequence is the Fibonacci sequence: 0, 1, 1, 2, 3, 5, 8, 13, 21,... For this sequence, the first two numbers are 0 and 1. Every number after that is calculated by adding the two previous numbers: a 3 = = 1 a 4 = = 2 a 5 = = 3 a 6 = = 5 a 7 = = 8 a 8 = = 13 a 9 = = 21
27 Examples Find the first five terms of each sequence. 1. a n+1 = a n, a 1 = 256
28 Examples Find the first five terms of each sequence. 1. a n+1 = a n, a 1 = 256 a 1 = 256, a 2 = 16, a 3 = 4, a 4 = 2, a 5 = 2
29 Examples Find the first five terms of each sequence. 1. a n+1 = a n, a 1 = 256 a 1 = 256, a 2 = 16, a 3 = 4, a 4 = 2, a 5 = 2 2. a n+1 = a n a n 1, a 1 = 10, a 2 = 8
30 Examples Find the first five terms of each sequence. 1. a n+1 = a n, a 1 = 256 a 1 = 256, a 2 = 16, a 3 = 4, a 4 = 2, a 5 = 2 2. a n+1 = a n a n 1, a 1 = 10, a 2 = 8 a 1 = 10, a 2 = 8, a 3 = 18, a 4 = 10, a 5 = 8
31 Series and Sums
32 Definition Suppose you have an infinite sequence a n. The nth partial sum is the sum of the first n terms: S n = a 1 + a a n For example, if a n = n + 1, (a 1 = 2, a 2 = 3, a 3 = 4, a 4 = 5, a 5 = 6) S 5 = = 20
33 Sigma Notation To represent sums, we use the uppercase Greek letter sigma,. For example: 4 (2k 1) = (2 1 1) + (2 2 1) + (2 3 1) + (2 4 1) k=1 = = 16
34 Examples 1. Find the 6th partial sum of the sequence 5, 10, 15, 20,...
35 Examples 1. Find the 6th partial sum of the sequence 5, 10, 15, 20,
36 Examples 1. Find the 6th partial sum of the sequence 5, 10, 15, 20, Evaluate the sum: 4 j=1 3 j + 1
37 Examples 1. Find the 6th partial sum of the sequence 5, 10, 15, 20, Evaluate the sum: 4 j=1 3 j
38 Examples 1. Find the 6th partial sum of the sequence 5, 10, 15, 20, Evaluate the sum: 4 j=1 3 j Write the sum in sigma notation:
39 Examples 1. Find the 6th partial sum of the sequence 5, 10, 15, 20, Evaluate the sum: 4 j=1 3 j Write the sum in sigma notation: k=1 ( 1) k (k + 2) 2 k
MATH 2420 Discrete Mathematics Lecture notes
MATH 2420 Discrete Mathematics Lecture notes Series and Sequences Objectives: Introduction. Find the explicit formula for a sequence. 2. Be able to do calculations involving factorial, summation and product
COLLEGE ALGEBRA. Arithmetic & Geometric Sequences
COLLEGE ALGEBRA By: Sister Mary Rebekah www.survivormath.weebly.com Cornell-Style Fill in the Blank Notes and Teacher s Key Arithmetic & Geometric Sequences 1 Topic: Discrete Functions main ideas & questions
13 Searching for Pattern
13 Searching for Pattern 13.1 Pictorial Logic In this section we will see how to continue patterns involving simple shapes. Example Continue these patterns by drawing the next 5 shapes in each case: Solution
Use the given information to write the first 5 terms of the sequence and the 20 th term. 6. a1= 4, d= 8 7. a1= 10, d= -6 8.
Arithmetic Sequences Class Work Find the common difference in sequence, and then write the next 3 terms in the sequence. 1. 3, 7,11, 15, 2. 1, 8, 15, 22, 3. 5, 2, -1, -4, 4. 68, 56, 44, 32, 5. 1.3, 2.6,
Unit Nine Precalculus Practice Test Probability & Statistics. Name: Period: Date: NON-CALCULATOR SECTION
Name: Period: Date: NON-CALCULATOR SECTION Vocabulary: Define each word and give an example. 1. discrete mathematics 2. dependent outcomes 3. series Short Answer: 4. Describe when to use a combination.
Honors Precalculus Chapter 9 Summary Basic Combinatorics
Honors Precalculus Chapter 9 Summary Basic Combinatorics A. Factorial: n! means 0! = Why? B. Counting principle: 1. How many different ways can a license plate be formed a) if 7 letters are used and each
Sequence and Series Lesson 6. March 14, th Year HL Maths. March 2013
j 6th Year HL Maths March 2013 1 arithmetic arithmetic arithmetic quadratic arithmetic quadratic geometric 2 3 Arithmetic Sequence 4 5 check: check: 6 check 7 First 5 Terms Count up in 3's from 4 simplify
CHAPTER 8 REVIEW ALGEBRA 2 Name Per
CHAPTER 8 REVIEW ALGEBRA 2 Name Per Fill in the blanks. 1. 3. 7 3 2n is said to be in notation. 2. n= 1 k = 1 is a Greek letter called. ( k 4) is read as. Write the next term in the given sequence. Then
THE ASSOCIATION OF MATHEMATICS TEACHERS OF NEW JERSEY 2018 ANNUAL WINTER CONFERENCE FOSTERING GROWTH MINDSETS IN EVERY MATH CLASSROOM
THE ASSOCIATION OF MATHEMATICS TEACHERS OF NEW JERSEY 2018 ANNUAL WINTER CONFERENCE FOSTERING GROWTH MINDSETS IN EVERY MATH CLASSROOM CREATING PRODUCTIVE LEARNING ENVIRONMENTS WEDNESDAY, FEBRUARY 7, 2018
Arithmetic Sequences Read 8.2 Examples 1-4
CC Algebra II HW #8 Name Period Row Date Arithmetic Sequences Read 8.2 Examples -4 Section 8.2 In Exercises 3 0, tell whether the sequence is arithmetic. Explain your reasoning. (See Example.) 4. 2, 6,
Strings. A string is a list of symbols in a particular order.
Ihor Stasyuk Strings A string is a list of symbols in a particular order. Strings A string is a list of symbols in a particular order. Examples: 1 3 0 4 1-12 is a string of integers. X Q R A X P T is a
Study Guide and Intervention
0-7 Study Guide and Intervention A geometric sequence is a sequence in which each term after the nonzero first term is found by multiplying the previous term by a constant called the common ratio. Geometric
Recursive Sequences. EQ: How do I write a sequence to relate each term to the previous one?
Recursive Sequences EQ: How do I write a sequence to relate each term to the previous one? Dec 14 8:20 AM Arithmetic Sequence - A sequence created by adding and subtracting by the same number known as
PROBLEM 1 Do You See a Pattern?
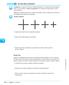PROBLEM 1 Do You See a Pattern? A sequence is a pattern involving an ordered arrangement of numbers, geometric figures, letters, or other objects. A term of a sequence is an individual number, figure,
Study Guide and Review - Chapter 3. Find the x-intercept and y-intercept of the graph of each linear function.
Find the x-intercept and y-intercept of the graph of each linear function. 11. The x-intercept is the point at which the y-coordinate is 0, or the line crosses the x-axis. So, the x-intercept is 8. The
Sequences. like 1, 2, 3, 4 while you are doing a dance or movement? Have you ever group things into
Math of the universe Paper 1 Sequences Kelly Tong 2017/07/17 Sequences Introduction Have you ever stamped your foot while listening to music? Have you ever counted like 1, 2, 3, 4 while you are doing a
Lecture 8: Recursing Recursively
Lecture 8: Recursing Recursively Alan Alda playing Richard Feynman in QED CS150: Computer Science University of Virginia Computer Science Now playing: JS Bach, The Art of Fugue Richard Feynman s Van (parked
DIFFERENT SEQUENCES. Learning Outcomes and Assessment Standards T 2 T 3
Lesson 21 DIFFERENT SEQUENCES Learning Outcomes and Assessment Standards Learning Outcome 1: Number and number relationships Assessment Standard Investigate number patterns including but not limited to
Study Guide and Review - Chapter 10. Find the indicated term of each arithmetic sequence. 11. a 1. = 9, d = 3, n = 14
Find the indicated term of each arithmetic sequence. 11. a 1 = 9, d = 3, n = 14 Substitute 9 for a 1, 3 for d, and 14 for n in the 14. a 1 = 1, d = 5, n = 18 Substitute 1 for a 1, 5 for d, and 18 for n
ECS 20 (Spring 2013) Phillip Rogaway Lecture 1
ECS 20 (Spring 2013) Phillip Rogaway Lecture 1 Today: Introductory comments Some example problems Announcements course information sheet online (from my personal homepage: Rogaway ) first HW due Wednesday
Maths lesson. Exploring sequences and the Fibonacci sequence. Learning objectives. Knowledge. Skills. Resources
Exploring sequences and the Fibonacci sequence Learning objectives 1. Explore the exponential sequences, leading to negative powers. 2. Discover the Fibonacci sequence and the Golden Number or Golden Ratio.
Algebra. Recap: Elements of Set Theory.
January 14, 2018 Arrangements and Derangements. Algebra. Recap: Elements of Set Theory. Arrangements of a subset of distinct objects chosen from a set of distinct objects are permutations [order matters]
LAMC Junior Circle January 22, Oleg Gleizer. The Hanoi Tower. Part 2
LAMC Junior Circle January 22, 2012 Oleg Gleizer The Hanoi Tower Part 2 Definition 1 An algorithm is a finite set of clear instructions to solve a problem. An algorithm is called optimal, if the solution
Grade 6 Math Circles February 21/22, Patterns - Solutions
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles February 21/22, 2017 Patterns - Solutions Tower of Hanoi The Tower of Hanoi is a
Notes for Recitation 3
6.042/18.062J Mathematics for Computer Science September 17, 2010 Tom Leighton, Marten van Dijk Notes for Recitation 3 1 State Machines Recall from Lecture 3 (9/16) that an invariant is a property of a
PRIMES IN SHIFTED SUMS OF LUCAS SEQUENCES. Lenny Jones Department of Mathematics, Shippensburg University, Shippensburg, Pennsylvania
#A52 INTEGERS 17 (2017) PRIMES IN SHIFTED SUMS OF LUCAS SEQUENCES Lenny Jones Department of Mathematics, Shippensburg University, Shippensburg, Pennsylvania lkjone@ship.edu Lawrence Somer Department of
In how many ways can we paint 6 rooms, choosing from 15 available colors? What if we want all rooms painted with different colors?
What can we count? In how many ways can we paint 6 rooms, choosing from 15 available colors? What if we want all rooms painted with different colors? In how many different ways 10 books can be arranged
Second Annual University of Oregon Programming Contest, 1998
A Magic Magic Squares A magic square of order n is an arrangement of the n natural numbers 1,...,n in a square array such that the sums of the entries in each row, column, and each of the two diagonals
UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS International General Certificate of Secondary Education
*3620551787* UNIVERSITY OF CAMBRIDGE INTERNATIONAL EXAMINATIONS International General Certificate of Secondary Education CAMBRIDGE INTERNATIONAL MATHEMATICS 0607/05 Paper 5 (Core) October/November 2010
Formal Verification. Lecture 5: Computation Tree Logic (CTL)
Formal Verification Lecture 5: Computation Tree Logic (CTL) Jacques Fleuriot 1 jdf@inf.ac.uk 1 With thanks to Bob Atkey for some of the diagrams. Recap Previously: Linear-time Temporal Logic This time:
CSE101: Design and Analysis of Algorithms. Ragesh Jaiswal, CSE, UCSD
Course Overview Graph Algorithms Algorithm Design Techniques: Greedy Algorithms Divide and Conquer Dynamic Programming Network Flows Computational Intractability Main Ideas Main idea: Break the given
LAMC Junior Circle February 3, Oleg Gleizer. Warm-up
LAMC Junior Circle February 3, 2013 Oleg Gleizer oleg1140@gmail.com Warm-up Problem 1 Compute the following. 2 3 ( 4) + 6 2 Problem 2 Can the value of a fraction increase, if we add one to the numerator
Fibonacci Numbers ANSWERS Lesson 1 of 10, work individually or in pairs
Lesson 1 of 10, work individually or in pairs In 1202, the mathematician Leonardo Pisano Fibonacci (pronounced fi-buh-nah-chee) published a book with the famous Fibonacci sequence in it. (A sequence is
Formulas for Primes. Eric Rowland Hofstra University. Eric Rowland Formulas for Primes / 27
Formulas for Primes Eric Rowland Hofstra University 2018 2 14 Eric Rowland Formulas for Primes 2018 2 14 1 / 27 The sequence of primes 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25
Grade 6 Math Circles February 21/22, Patterns
Faculty of Mathematics Waterloo, Ontario N2L 3G1 Centre for Education in Mathematics and Computing Grade 6 Math Circles February 21/22, 2017 Patterns Tower of Hanoi The Tower of Hanoi is a puzzle with
A slope of a line is the ratio between the change in a vertical distance (rise) to the change in a horizontal
The Slope of a Line (2.2) Find the slope of a line given two points on the line (Objective #1) A slope of a line is the ratio between the change in a vertical distance (rise) to the change in a horizontal
Repeated Games. ISCI 330 Lecture 16. March 13, Repeated Games ISCI 330 Lecture 16, Slide 1
Repeated Games ISCI 330 Lecture 16 March 13, 2007 Repeated Games ISCI 330 Lecture 16, Slide 1 Lecture Overview Repeated Games ISCI 330 Lecture 16, Slide 2 Intro Up to this point, in our discussion of extensive-form
Goldbach Conjecture (7 th june 1742)
Goldbach Conjecture (7 th june 1742) We note P the odd prime numbers set. P = {p 1 = 3, p 2 = 5, p 3 = 7, p 4 = 11,...} n 2N\{0, 2, 4}, p P, p n/2, q P, q n/2, n = p + q We call n s Goldbach decomposition
Eric Duchêne (Univ. Claude Bernard Lyon 1) Michel Rigo (University of Liège)
INVARIANT GAMES Eric Duchêne (Univ. Claude Bernard Lyon 1) Michel Rigo (University of Liège) http://www.discmath.ulg.ac.be/ Words 2009, Univ. of Salerno, 14th September 2009 COMBINATORIAL GAME THEORY FOR
With Question/Answer Animations. Chapter 6
With Question/Answer Animations Chapter 6 Chapter Summary The Basics of Counting The Pigeonhole Principle Permutations and Combinations Binomial Coefficients and Identities Generalized Permutations and
European Journal of Combinatorics. Staircase rook polynomials and Cayley s game of Mousetrap
European Journal of Combinatorics 30 (2009) 532 539 Contents lists available at ScienceDirect European Journal of Combinatorics journal homepage: www.elsevier.com/locate/ejc Staircase rook polynomials
An old pastime.
Ringing the Changes An old pastime http://www.youtube.com/watch?v=dk8umrt01wa The mechanics of change ringing http://www.cathedral.org/wrs/animation/rounds_on_five.htm Some Terminology Since you can not
Restricted Permutations Related to Fibonacci Numbers and k-generalized Fibonacci Numbers
Restricted Permutations Related to Fibonacci Numbers and k-generalized Fibonacci Numbers arxiv:math/0109219v1 [math.co] 27 Sep 2001 Eric S. Egge Department of Mathematics Gettysburg College 300 North Washington
Chapter 1. Set Theory
Chapter 1 Set Theory 1 Section 1.1: Types of Sets and Set Notation Set: A collection or group of distinguishable objects. Ex. set of books, the letters of the alphabet, the set of whole numbers. You can
Precalc Unit 10 Review
Precalc Unit 10 Review Name: Use binomial expansion to expand. 1. 2. 3.. Use binomial expansion to find the term you are asked for. 4. 5 th term of (4x-3y) 8 5. 3 rd term of 6. 4 th term of 7. 2 nd term
Digital Communications: A Discrete-Time Approach M. Rice. Errata
Digital Communications: A Discrete-Time Approach M. Rice Errata Foreword Page xiii, first paragraph, bare witness should be bear witness Page xxi, last paragraph, You know who you. should be You know who
PARTICIPANT Guide. Unit 2
PARTICIPANT Guide Unit 2 UNIT 02 participant Guide ACTIVITIES NOTE: At many points in the activities for Mathematics Illuminated, workshop participants will be asked to explain, either verbally or in
BCD Adder. Lecture 21 1
BCD Adder -BCD adder A 4-bit binary adder that is capable of adding two 4-bit words having a BCD (binary-coded decimal) format. The result of the addition is a BCD-format 4-bit output word, representing
The Product Rule The Product Rule: A procedure can be broken down into a sequence of two tasks. There are n ways to do the first task and n
Chapter 5 Chapter Summary 5.1 The Basics of Counting 5.2 The Pigeonhole Principle 5.3 Permutations and Combinations 5.5 Generalized Permutations and Combinations Section 5.1 The Product Rule The Product
Combinatorial Expressions Involving Fibonacci, Hyperfibonacci, and Incomplete Fibonacci Numbers
1 2 3 47 6 23 11 Journal of Integer Sequences, Vol. 17 (2014), Article 14.4.3 Combinatorial Expressions Involving Fibonacci, Hyperfibonacci, and Incomplete Fibonacci Numbers Hacène Belbachir and Amine
Solutions to Part I of Game Theory
Solutions to Part I of Game Theory Thomas S. Ferguson Solutions to Section I.1 1. To make your opponent take the last chip, you must leave a pile of size 1. So 1 is a P-position, and then 2, 3, and 4 are
7.4 Permutations and Combinations
7.4 Permutations and Combinations The multiplication principle discussed in the preceding section can be used to develop two additional counting devices that are extremely useful in more complicated counting
Important Distributions 7/17/2006
Important Distributions 7/17/2006 Discrete Uniform Distribution All outcomes of an experiment are equally likely. If X is a random variable which represents the outcome of an experiment of this type, then
Research Article n-digit Benford Converges to Benford
International Mathematics and Mathematical Sciences Volume 2015, Article ID 123816, 4 pages http://dx.doi.org/10.1155/2015/123816 Research Article n-digit Benford Converges to Benford Azar Khosravani and
NIM Games: Handout 1
NIM Games: Handout 1 Based on notes by William Gasarch 1 One-Pile NIM Games Consider the following two-person game in which players alternate making moves. There are initially n stones on the board. During
Elementary Combinatorics
184 DISCRETE MATHEMATICAL STRUCTURES 7 Elementary Combinatorics 7.1 INTRODUCTION Combinatorics deals with counting and enumeration of specified objects, patterns or designs. Techniques of counting are
Chapter 4: Patterns and Relationships
Chapter : Patterns and Relationships Getting Started, p. 13 1. a) The factors of 1 are 1,, 3,, 6, and 1. The factors of are 1,,, 7, 1, and. The greatest common factor is. b) The factors of 16 are 1,,,,
Name Date. Goal: Understand sets and set notation.
F Math 12 3.1 Types of Sets and Set Notation p. 146 Name Date Goal: Understand sets and set notation. 1. set: A collection of distinguishable objects; for example, the set of whole numbers is W = {0, 1,
n! = n(n 1)(n 2) 3 2 1
A Counting A.1 First principles If the sample space Ω is finite and the outomes are equally likely, then the probability measure is given by P(E) = E / Ω where E denotes the number of outcomes in the event
29. Army Housing (a) (b) (c) (d) (e) (f ) Totals Totals (a) (b) (c) (d) (e) (f) Basketball Positions 32. Guard Forward Center
Infinite Sets and Their Cardinalities As mentioned at the beginning of this chapter, most of the early work in set theory was done by Georg Cantor He devoted much of his life to a study of the cardinal
CSL 356: Analysis and Design of Algorithms. Ragesh Jaiswal CSE, IIT Delhi
CSL 356: Analysis and Design of Algorithms Ragesh Jaiswal CSE, IIT Delhi Techniques Greedy Algorithms Divide and Conquer Dynamic Programming Network Flows Computational Intractability Dynamic Programming
MAT 1160 Mathematics, A Human Endeavor
MAT 1160 Mathematics, A Human Endeavor Syllabus: office hours, grading Schedule (note exam dates) Academic Integrity Guidelines Homework & Quizzes Course Web Site : www.eiu.edu/ mathcs/mat1160/ 2005 09,
Staircase Rook Polynomials and Cayley s Game of Mousetrap
Staircase Rook Polynomials and Cayley s Game of Mousetrap Michael Z. Spivey Department of Mathematics and Computer Science University of Puget Sound Tacoma, Washington 98416-1043 USA mspivey@ups.edu Phone:
MAT Mathematics in Today's World
MAT 1000 Mathematics in Today's World Last Time 1. Three keys to summarize a collection of data: shape, center, spread. 2. The distribution of a data set: which values occur, and how often they occur 3.
5. (1-25 M) How many ways can 4 women and 4 men be seated around a circular table so that no two women are seated next to each other.
A.Miller M475 Fall 2010 Homewor problems are due in class one wee from the day assigned (which is in parentheses. Please do not hand in the problems early. 1. (1-20 W A boo shelf holds 5 different English
First Group Second Group Third Group How to determine the next How to determine the next How to determine the next number in the sequence:
MATHEMATICIAN DATE BAND PUZZLES! WHAT COMES NEXT??? PRECALCULUS PACKER COLLEGIATE INSTITUTE Warm Up: 1. You are going to be given a set of cards. The cards have a sequence of numbers on them Although there
An elementary study of Goldbach Conjecture
An elementary study of Goldbach Conjecture Denise Chemla 26/5/2012 Goldbach Conjecture (7 th, june 1742) states that every even natural integer greater than 4 is the sum of two odd prime numbers. If we
The Problem. Tom Davis December 19, 2016
The 1 2 3 4 Problem Tom Davis tomrdavis@earthlink.net http://www.geometer.org/mathcircles December 19, 2016 Abstract The first paragraph in the main part of this article poses a problem that can be approached
Suppose you are supposed to select and carry out oneof a collection of N tasks, and there are T K different ways to carry out task K.
Addition Rule Counting 1 Suppose you are supposed to select and carry out oneof a collection of N tasks, and there are T K different ways to carry out task K. Then the number of different ways to select
NUMBER PATTERNS. The first 3 triangular numbers can be illustrated as follows: 1 2 3
1 NUMBER PATTERNS EXERCISE 1 1. Write down the first 20 Natural Numbers. 2. Provide answers to the following: a. What are the 4 th, 5 th and 6 th even numbers? b. What relationship is between an even number
Beyond Infinity? Joel Feinstein. School of Mathematical Sciences University of Nottingham
Beyond Infinity? Joel Feinstein School of Mathematical Sciences University of Nottingham 2006-2007 The serious mathematics behind this talk is due to the great mathematicians David Hilbert (1862 1943)
Pre-Calculus Semester 1
Pre-Calculus Semester 1 Created By: Jennifer Suby and Kay Knutson Oswego East High School Fall 2015 Sequences & Series 1 2 Sequences and Series Day 1 Notes: Arithmetic Sequences Sequences Sequence: a function
Combinatorial Proofs
Combinatorial Proofs Two Counting Principles Some proofs concerning finite sets involve counting the number of elements of the sets, so we will look at the basics of counting. Addition Principle: If A
Distribution of Aces Among Dealt Hands
Distribution of Aces Among Dealt Hands Brian Alspach 3 March 05 Abstract We provide details of the computations for the distribution of aces among nine and ten hold em hands. There are 4 aces and non-aces
Once you get a solution draw it below, showing which three pennies you moved and where you moved them to. My Solution:
Arrange 10 pennies on your desk as shown in the diagram below. The challenge in this puzzle is to change the direction of that the triangle is pointing by moving only three pennies. Once you get a solution
@CRC Press. Discrete Mathematics. with Ducks. sarah-marie belcastro. let this be your watchword. serious mathematics treated with levity
Discrete Mathematics with Ducks sarah-marie belcastro serious mathematics treated with levity let this be your watchword @CRC Press Taylor & Francis Croup Boca Raton London New York CRC Press is an imprint
A collection of 9-1 Maths GCSE Sample and Specimen questions from AQA, OCR, Pearson-Edexcel and WJEC Eduqas. Name: Total Marks:
Sequences (F) A collection of 9-1 Maths GCSE Sample and Specimen questions from AQA, OCR, Pearson-Edexcel and WJEC Eduqas. Name: Total Marks: 1. Here are the first three patterns in a sequence. (a) Draw
Facilitator Guide. Unit 2
Facilitator Guide Unit 2 UNIT 02 Facilitator Guide ACTIVITIES NOTE: At many points in the activities for Mathematics Illuminated, workshop participants will be asked to explain, either verbally or in
CS100: DISCRETE STRUCTURES. Lecture 8 Counting - CH6
CS100: DISCRETE STRUCTURES Lecture 8 Counting - CH6 Lecture Overview 2 6.1 The Basics of Counting: THE PRODUCT RULE THE SUM RULE THE SUBTRACTION RULE THE DIVISION RULE 6.2 The Pigeonhole Principle. 6.3
Chapter 7. Intro to Counting
Chapter 7. Intro to Counting 7.7 Counting by complement 7.8 Permutations with repetitions 7.9 Counting multisets 7.10 Assignment problems: Balls in bins 7.11 Inclusion-exclusion principle 7.12 Counting
Siyavula textbooks: Grade 12 Maths. Collection Editor: Free High School Science Texts Project
Siyavula textbooks: Grade 12 Maths Collection Editor: Free High School Science Texts Project Siyavula textbooks: Grade 12 Maths Collection Editor: Free High School Science Texts Project Authors: Free
a) 2, 4, 8, 14, 22, b) 1, 5, 6, 10, 11, c) 3, 9, 21, 39, 63, d) 3, 0, 6, 15, 27, e) 3, 8, 13, 18, 23,
Pre-alculus Midterm Exam Review Name:. Which of the following is an arithmetic sequence?,, 8,,, b),, 6, 0,, c), 9,, 9, 6, d), 0, 6,, 7, e), 8,, 8,,. What is a rule for the nth term of the arithmetic sequence
Limitations of Sum-of-Sinusoid Signals
Limitations of Sum-of-Sinusoid Signals I So far, we have considered only signals that can be written as a sum of sinusoids. x(t) =A 0 + N Â A i cos(2pf i t + f i ). i=1 I For such signals, we are able
Name: Exam 1. September 14, 2017
Department of Mathematics University of Notre Dame Math 10120 Finite Math Fall 2017 Name: Instructors: Basit & Migliore Exam 1 September 14, 2017 This exam is in two parts on 9 pages and contains 14 problems
Countability. Jason Filippou UMCP. Jason Filippou UMCP) Countability / 12
Countability Jason Filippou CMSC250 @ UMCP 06-23-2016 Jason Filippou (CMSC250 @ UMCP) Countability 06-23-2016 1 / 12 Outline 1 Infinity 2 Countability of integers and rationals 3 Uncountability of R Jason
Evacuation and a Geometric Construction for Fibonacci Tableaux
Evacuation and a Geometric Construction for Fibonacci Tableaux Kendra Killpatrick Pepperdine University 24255 Pacific Coast Highway Malibu, CA 90263-4321 Kendra.Killpatrick@pepperdine.edu August 25, 2004
Hausdorff dimension in groups acting on trees
of spinal groups in groups acting on trees University of the Basque Country, Bilbao Group St Andrews, Bath, August 4th 2009 in groups acting on trees of spinal groups Contents 1 2 3 of spinal groups in
The Greek Alphabet Aα Alpha Γγ Gamma
Lecture 3 Cartesian The Greek Alphabet Aα Alpha Γγ Gamma Eɛε Epsilon Hη Eta Iι Iota Λλ Lambda Nν Nu Oo Omicron Pρ Rho Tτ Tau Φφϕ Phi Ψψ Psi Bβ Beta δ Delta Zζ Zeta Θθ Theta Kκ Kappa Mµ Mu Ξξ Xi Ππ Pi Σσς
DIGITAL SIGNAL PROCESSING WITH VHDL
DIGITAL SIGNAL PROCESSING WITH VHDL GET HANDS-ON FROM THEORY TO PRACTICE IN 6 DAYS MODEL WITH SCILAB, BUILD WITH VHDL NUMEROUS MODELLING & SIMULATIONS DIRECTLY DESIGN DSP HARDWARE Brought to you by: Copyright(c)
Three Pile Nim with Move Blocking. Arthur Holshouser. Harold Reiter.
Three Pile Nim with Move Blocking Arthur Holshouser 3600 Bullard St Charlotte, NC, USA Harold Reiter Department of Mathematics, University of North Carolina Charlotte, Charlotte, NC 28223, USA hbreiter@emailunccedu
Game Theory and Algorithms Lecture 19: Nim & Impartial Combinatorial Games
Game Theory and Algorithms Lecture 19: Nim & Impartial Combinatorial Games May 17, 2011 Summary: We give a winning strategy for the counter-taking game called Nim; surprisingly, it involves computations
Meet #3 January Intermediate Mathematics League of Eastern Massachusetts
Meet #3 January 2009 Intermediate Mathematics League of Eastern Massachusetts Meet #3 January 2009 Category 1 Mystery 1. How many two-digit multiples of four are there such that the number is still a
Lecture 3 Complex Exponential Signals
Lecture 3 Complex Exponential Signals Fundamentals of Digital Signal Processing Spring, 2012 Wei-Ta Chu 2012/3/1 1 Review of Complex Numbers Using Euler s famous formula for the complex exponential The
LUCAS-SIERPIŃSKI AND LUCAS-RIESEL NUMBERS
LUCAS-SIERPIŃSKI AND LUCAS-RIESEL NUMBERS DANIEL BACZKOWSKI, OLAOLU FASORANTI, AND CARRIE E. FINCH Abstract. In this paper, we show that there are infinitely many Sierpiński numbers in the sequence of
Section Introduction to Sets
Section 1.1 - Introduction to Sets Definition: A set is a well-defined collection of objects usually denoted by uppercase letters. Definition: The elements, or members, of a set are denoted by lowercase
Summary Overview of Topics in Econ 30200b: Decision theory: strong and weak domination by randomized strategies, domination theorem, expected utility
Summary Overview of Topics in Econ 30200b: Decision theory: strong and weak domination by randomized strategies, domination theorem, expected utility theorem (consistent decisions under uncertainty should
constant EXAMPLE #4:
Linear Equations in One Variable (1.1) Adding in an equation (Objective #1) An equation is a statement involving an equal sign or an expression that is equal to another expression. Add a constant value
UCI Math Circle October 10, Clock Arithmetic
UCI Math Circle October 10, 2016 Clock Arithmetic 1. Pretend that it is 3:00 now (ignore am/pm). (a) What time will it be in 17 hours? (b) What time was it 22 hours ago? (c) The clock on the right has
Theory of Probability - Brett Bernstein
Theory of Probability - Brett Bernstein Lecture 3 Finishing Basic Probability Review Exercises 1. Model flipping two fair coins using a sample space and a probability measure. Compute the probability of
NOTES ON SEPT 13-18, 2012
NOTES ON SEPT 13-18, 01 MIKE ZABROCKI Last time I gave a name to S(n, k := number of set partitions of [n] into k parts. This only makes sense for n 1 and 1 k n. For other values we need to choose a convention