Spiral Tilings with C-curves
|
|
|
- Robert Sims
- 5 years ago
- Views:
Transcription
1 Spirl Tilings with -curves Using ombintorics to Augment Trdition hris K. Plmer 19 North Albny Avenue hicgo, Illinois, 0 chris@shdowfolds.com Abstrct Spirl tilings used by rtisns through the ges using -curves re identified. The complete combintoric set of these tiles is determined nd tilings tht cn be mde with them re exmined. 1. Introduction Throughout the history of ornment rtisns from mny cultures hve composed ptterns utilizing spirls. Mny of the compositions mde by these rtisns cn be understood s the substitutions of -curves or S- curves or combintion of -curves nd S-curves for the stright lines of monohedrl or polyhedrl tiling [1]. The subject of this pper is the subset of these tilings composed with -curves. Those known nd used by trditionl crftsmen re shown below in Figures 1 nd 2 [2]. Artisns cn pply nd hve pplied n enormous vriety of styles using these three tilings. An exmple of this vriety cn be seen by observing the expression of the sme tiling, (...), in two different styles, simple form in Figure 1 nd eltic style in Figure 2. These underlying tilings re prt of set of tilings with regulr vertices commonly known s Lves tilings []. This pper identifies the complete set of tiles nd exmines some properties of the tilings tht cn be mde with them. This gretly ugments the number of underlying tilings vilble for use by rtisns from three to n infinite number of tilings []. Figure 1 (c) Figure 2 (c)
2 In generl terms, our problem is: 2. The Problem Wht tilings of the plne llow for -curves to be substituted for the edges of the tiles We will restrict the problem by imposing the following conditions: i) Spirls must be produced t ll the vertices. ii) The ngles surrounding ny vertex of the tiling must ll be equl. [] As we shll see these tilings re very restricted, but there re nevertheless such lrge number of different kinds tht we cn expect to be ble to clssify them only in some wek sense. As will be described third condition results: iii) Ech tile must hve n even number of sides. Figure ondition ii) shows tht the ngles t vertex tht lies on n edges must be equl to 0 /n. ondition iii) holds becuse the spirl property i) entils tht for ny two -curves tht will be substituted for djcent edges of tile one will lie inside the polygon nd one outside. This lterntion cn only be consistently continued round the whole tile if tht tile hs n even number of sides s shown in Figure. The tile in Figure b stisfies condition ii) but not condition iii) cusing contrdiction of condtion i). onversely, however, if we re given ny tiling stisfying conditions ii) nd iii), then fter ssigning clockwise or counterclockwise orienttion rbitrrily to ny one vertex, we cn consistently ssign such orienttions to the other vertices by lterntion. This shows tht in generl there re two wys of orienting the spirls for given tiling.. The Possible Types of Tile We shll sy tht vertex hs type n when it belongs to just n tiles, which will ll hve ngles of 0 /n there. An edge whose two vertices hve types nd b will be sid to hve type (.b), nd tile will be sid to hve type (.b.c.,... k) if its vertices, reding cycliclly (in either direction) hve types,b,c,...,k. Theorem 1. The only possible types of polyhedrl or monohedrl tiles tht cover the plne nd llow -curves to be substituted for the lines nd stisfy conditions i), ii) nd iii) re:! (...) Figure (...) (...) (...) (...) (...) (...) (...) Proof. Since the interior ngle of tile t n n-fold vertex is 0 /n, the exterior ngle is /n. Now for:
3 n 0/n 180 0/n > < >150 Tble 1 The sum of the exterior ngles of polygon is lwys 0! Since Tble 1 shows tht the smllest vlue for n exterior ngle in these tiles is 0, there cn be t most ngles per tile, nd if there re, tht tile must be of type (...). Otherwise, since the tile must hve n even number of sides, it must in fct be qudrilterl, with n verge exterior ngle of 90, nd smllest one of either 0 or 90. If there re (t lest) two of 0, the sum of the remining two is 20, nd from Tble 1 we hve only two possibilities: nd , corresponding to types (...) nd (...) 0 + 0, corresponding to types (...) nd (...). If there is precisely one such 0 exterior ngle, the sum of the other three must be 00, which forces the lest to be 90, forcing nother 90 ngle nd leving precisely 0 for the lst one, corresponding to: (...) nd (...). Finlly, if there is no 0 ngle, ll four ngles must be 90, since this is now both the smllest possible vlue nd lso their verge vlue, nd we hve the only reming type: (...). nd this completes the proof. c We remrk tht the ngles of these tiles do not suffice to determine their shpes: for instnce tile of type (...) might be ny shpe of rectngle. However, we shll regrd tiling s well-enough determined when we hve specified ll the ngles of its tiles. There is then cnonicl tiling with these ngles, obtined by using tiles with the prticulr dimensions shown in Figure. From now on we shll lwys drw only these cnonicl tilings.. Tilings With Type Vertex. Theorem 2. No tiling involves tile of type (...), nd there is combintorilly only one tiling tht involves one of type (...). F D E A B Figure 5 Figure Proof. We exmine the type vertex of tile A of type (...) shown in Figure 5. If both the djcent tiles B nd t this vertex hve tye (...) then the tiles D nd E of Figure re forced to hve types (...), nd the tile F between them hs n impossible type (...). So we cn suppose tht B hs type (...) s in Figure, nd this forces the tile of tht Figure to hve type (...). The numbers p nd q of tht Figure must be nd in some order. But if q, then r, mking tile F to hve the impossible shpe (..,). So we must hve p, q, nd so r, nd gin F hs n impossible type, (...). A p B q r
4 A B Figure 7 Figure 8 Now tht we hve dismissed type (...), we see tht ll the tiles with ny type vertex of type (...) must hve tht type, forming rosette s in Figure 7 nd the tile of tht Figure hs type (...) which cn only be (...). This in turn forces tiles D nd E to hve type (...), yielding two more rosettes round vertices Y nd Z. Now it is cler tht the tiling continues uniquely s in Figure 8 thus concluding the proof. c 5. Tilings with Edges of Type (.) or (.) Theorem. If tiling hs n edge of type (.) or (.), it must be one of the tilings H, H1, H2,.., Hh, or Hh* of Figures 9-. H Figure 9 H1 Figure 10 H2 Hh Figure 11 Figure Proof. The only types tht contin two djcent s re (...) nd (...). The ltter is lso the only type contining two djcent s. So it follows tht if one edge of tile is of type (.), then the opposite edge is either (.) or (.), while the edge opposite to one of type (.) is necessrily of type (.). Hh* Figure 1 The tiles contining ll these opposite pirs of edges therefore form ccordion-rows like tht of Figure 1, ech such row consisting of n infinity of hexgons ech of which is either single tile of type (...) or is split into two tiles of type (...). We suppose first tht some ccordion-row does contin two unsplit hexgons, nd select one for which these hexgons (A1 nd A2) re seprted by the smllest possible number of tiles (B) tht hppens in tht
5 A A E``` ``` E```` E```` ```` ```` F``` F``` D``` E``` ``` E`` F`` F`` F`` F`` `` D`` D`` E`` `` E` F` F` F` F` F` F` E` ` D` D` D` ` Figure 1 E F F F F F F F F E D D D D A1 B B B B B B B B B B A2 tiling (Figure 1). Then the two tiles mrked in the Figure hve type (... ) tht cn only be (...), nd we cn lso determine the type of the tiles mrked D, since (... ) cn only be (...). We cn proceed upwrds in this wy, forcing ll the types of tiles (nd so the shpe of the Figure) until we conclude triumphntly tht there must be third hexgonl tile t A. In the third row, for exmple, we cn see tht the end tiles E hve type (...) (...), nd this forces type of F1 to be (...) (...), which in turn forces F2 to to hve type (...) (...), nd so on. The rgument then repets, with row of tiles ' nd D' behving like nd D followed by one of tiles E' nd F' behving like E nd the Fi, nd so on, until just below the summit we hve row of just two tiles ''''... surmounted by one of just two tiles E''''.... The tile A t the summit hs type (......) which cn only be hexgon (...). We hve found n equilterl tringle of tiles whose vertices re A1, A2, nd A. But we could repet the rgument to show tht butting this tringle long its edge A2 A there is nother one, with vertices A2, A, A. In the cse illustrted in Figure 1, the centers of ny two nerest unsplit hexgons re seprted by units, nd so we cll this the tiling H. But the seprtion could be ny positive integer. The rgument lso hndles the cse when n ccordion-row contins only one unsplit hexgon which is nturl to cll Hh (Figure 11), nd tht in which it hs no unsplit hexgon, Hh* (Figure ). This concludes the proof. c. The Tiling With No Vertex of Type At ny time from now on, the tilings we hve lredy found will be clled the old tilings. Any new tiling cn hve tiles of only the types: (...), (...), (...), (...). Theorem. The only new tiling with no vertex of type is the rhombic tiling R of Figure 15. Figure 15 Proof. Plinly ll its tiles must hve type (...), nd moment s thought suffices to show tht these cn only but s in Figure 15. c
6 7. Tilings With Line of Type (...,...,...) We sy tht stright line hs type (...,...,...) if it consists entirely of type (.) edges of the tiling. (c) (d) Figure 1 (Some exmples of mny possible rrngements of prllel tilings ) Theorem 5. The only tilings contining such line re the prllel tilings illustrted in Figure 1. Proof. We consider the tiles tht but the given line on one side. Any chosen one of these hs type (...) which cn only be (...) s in Figure 17 or (...) s in Figure 18. In the first cse the tiles neighboring the given one hve shpes (...) which mkes them lso (...), nd inductively we see tht in fct ll the tiles on tht side hve tht type, nd re bounded bove by nother of type (...,...,...). B A A A A A A B In Figure 18 the neighboring types re (...) or (...), nd so re necessrily (...), nd we see gin tht ll the tiles (A) on tht side of the line hve this type. But this time they re bounded bove by zig-zg line whose vertices re lterntely of types nd. The tiles (B) tht but them from bove hve types (...) (...), nd we obtin Figure 18b. The tiles () bove these hve types (...) which my be either (...) or (...), nd it is gin esy to see tht in fct ll of them must hve the sme one of these types. If this is (...) they re bounded Figure 18 Figure 17
7 bove by nother line of type (...,...,...) (hinted t by the dotted line in Figure 18b). If not, we hve nother row (D) of horizontl rhombs (...), nd so on. c 8. Ptches nd the Prity Rule From now on, we shll seprte the edges of our tilings into two clsses, indicted by thick nd thin lines. We mke this decision rbitrrily for one edge, nd then continue by using the rule tht ny pir of djcent edges of tile re to be the sme thickness if they but t type or vertex, but of different thickness if they but type vertex. This rule is consistent round ny tile becuse ll possible types hve n even number of type vertices, nd round ny vertex becuse we cn mke its edges ll hve the sme thickness if it hs type or, or lternting thicknesses if it hs type. The thick edges now divide the tiling into regions which we shll cll ptches, consisting of vrious numbers of tiles. The edges of ptch will consist of chins of edges of the underlying tiling, with possibly some internl verticies which must ll be of type nd end vertices which must be of type or. Plinly ny vertex in the interior of ptch must hve type or, nd two djcent such vertices must be one of ech type (in new tiling). An exmple is shown in Figure 19. Figure 19 We shll now prove wht we cll The Prity Rule : Theorem. The two ends of n edge of ptch tht hs ny internl vertices re of the sme type ( or ) if tht edge hs n odd number of internl vertices; of opposite types (one, one ) if it involves n even number. Figure 20 Proof. As in the proof of Theorem 5, the tiles tht but this edge inside the ptch must ll hve type (...) except for the two t the ends. Figure 20 shows three possibilities: we see tht these tiles re bounded on the side wy from the edge of the ptch by zigzg line whose ends hve type, while the others hve lterntely types nd. Since the only possible type for the two end tiles is (...) the ends of the edge must hve the types opposite to those of the outermost internl vertices of this zigzg, which estblishes the theorem. c
8 Figure 21 There cn exist ptches tht violte the prity rule, but they my contin no internl vertices. It is esy to see tht ny ptch contining no internl vertices is of one of the shpes shown in Figure 21. (Not ll of these violte the prity rule.) Theorem 7. Any tiling with ptch tht violtes the prity rule is one of the Prllel Tilings found in Theorem 5. Proof. If one edge of ptch violtes the Prity Rule, then we see from Figure 21 tht so does the opposite edge. The ptches djcent to the given one long these edges must lso be in Figure 21, since they eqully violte the rule. We cn continue in this wy to obtin n infinite concertin of such ptches, which we see contins some lines of type (...,...,...), nd so must be covered by Theorem 5. So no new Tiling cn contin ny edge tht violtes the Prity Rule. This concludes the proof. c 9. The Difference Rule, nd the Shpes of Ptches Since ech vertex ngle of ptch is either 0 or 0, ptch cn be t most hexgonl. We shll stte nd prove the Difference Rule first for hexgonl ptches, since this is in wy the most generl cse. b 9 5 A 7 5 c Figure 22 B 11 Theorem 8. For hexgonl ptch, the numbers A,b,,,B,c of lines tht cross the successive edges of the ptch (see Figure 22) obey the Difference Rule : A B b c. b g Figure 2 b g Proof. We introduce three scores, b, g, tht re ttched to the ends of the thin edges of tiles ccording to the direction in which they point, s in Figure 2. Since the two ends of ny edge cncel, the totl scores of ALL the edge-ends in our ptch must ll be zero.
9 b Figure 2 b b -g -b -b - g -g b - b -b - g g -g b -g -b - b g -b - g -g b -b - g -g b - b g -b - g - g 0 b - -bg 1 - b 1 g Now s seen in Figure 2 the three edge-ends t type vertex hve either: b g 1 or b g 1, while the totls for the six edge-ends t type vertex re b g 0. It follows tht if we sum over ll edge-ends t ll internl vertices of ptch, the three scores stisfy b g, nd therefore the sme must be true for the scores of the edge-ends t boundry vertices of the ptch. But for these the scores re A, b B b, g c, proving the rule. The possible shpes of ptch re shown in Figure 25. The second nd third rows of this figure show the smllest ptches possible which do not contin the rhombic tiling R. The finite ones cn be regrded s hexgons in which some edges hve length zero (nd so contribute zero to the pproprite score), nd so the Difference Rule nd its proof continues to hold for them. The infinite ptches shown in Figure 2 cn lso be regrded s hexgons in which some edges hve infinite length, while others hve receded to infinity. The proof of the Difference Rule fils, becuse the sums involved become infinite; nd in fct those of the numbers A,b,,,B,c tht survive re only restricted by the Prity Rule. This concludes the proof. c 10. All Remining Tilings All the tilings not lredy discussed re obtined from tesselltions of the plne by pieces of the shpes indicted in Figure 25 in the following wy. We ttch to ech finite edge number, which is the number of thin edges which tht edge is to cross. These numbers must stisfy the Prity Rule, nd for finite ptches lso the Difference Rule. If they do so, they determine unique tiling, in which ech ptch is filled by portion of the rhombic tiling R. These ptches my be combined with the ptches shown in Figure 21. Figure 25
10 Figure 2 One exmple of composition using trditionl eltic style to express one of the new underlying tilings presented in this pper cn be seen t the front of the Bridges Section. Below re the five sphericl tilings with regulr vertices tht llow -curves. Acknowledgment I thnk Professor John onwy of the University of Princeton for spending hours of his time to help put my rguments into mthemticl lnguge nd dedicte this pper to him. References [1] The complete set of tiles tht includes S-curves, -curves nd combintions of S-curves nd -curves, study of those compositions used by trditionl rtisns nd mny tht ugment trdition utilizing them is presented in Scurls nd Whirl Spools by hris K. Plmer, VisMth Volume 10. [2] Some interesting exmples of trditionl compositions tht use tilings with irregulr underlying tilings not ddressed by this pper cn be seen in eltic Art the methods of onstruction, George Bin, Dover ISBN , pge pltes 11-. Pges -5 Pltes 7-10 contin exmples of frieze ptterns nd rosettes utilizings spirls lso not ddressed in this pper. [] After the fmous crytllogrpher Fritz Lves. See Tilings nd Ptterns, Grunbum nd Sheprd, ISBN , pges [] Recursive methods developed by the uthor from 1997 to the present show tht within the restrictions imposed by the rules described in this pper n infinite vriety of spirl tilings cn be composed. These will be presented in forthcoming ppers nd s prt of doctorl thesis. The principles presented in this pper pply for tilings on spheres: Hyperbolic tilings cn lso be composed with these tiles nd the ddition of other even sided tiles.
Math Circles Finite Automata Question Sheet 3 (Solutions)
 Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Domination and Independence on Square Chessboard
 Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY
 LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
First Round Solutions Grades 4, 5, and 6
 First Round Solutions Grdes 4, 5, nd 1) There re four bsic rectngles not mde up of smller ones There re three more rectngles mde up of two smller ones ech, two rectngles mde up of three smller ones ech,
First Round Solutions Grdes 4, 5, nd 1) There re four bsic rectngles not mde up of smller ones There re three more rectngles mde up of two smller ones ech, two rectngles mde up of three smller ones ech,
Geometric quantities for polar curves
 Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Example. Check that the Jacobian of the transformation to spherical coordinates is
 lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations
 54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
SOLVING TRIANGLES USING THE SINE AND COSINE RULES
 Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Lecture 20. Intro to line integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Section 16.3 Double Integrals over General Regions
 Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
CS 135: Computer Architecture I. Boolean Algebra. Basic Logic Gates
 Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
MATH 118 PROBLEM SET 6
 MATH 118 PROBLEM SET 6 WASEEM LUTFI, GABRIEL MATSON, AND AMY PIRCHER Section 1 #16: Show tht if is qudrtic residue modulo m, nd b 1 (mod m, then b is lso qudrtic residue Then rove tht the roduct of the
MATH 118 PROBLEM SET 6 WASEEM LUTFI, GABRIEL MATSON, AND AMY PIRCHER Section 1 #16: Show tht if is qudrtic residue modulo m, nd b 1 (mod m, then b is lso qudrtic residue Then rove tht the roduct of the
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN. Inventor: Brian L. Baskin
 METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
REVIEW, pages
 REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
Student Book SERIES. Patterns and Algebra. Name
 E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
Exercise 1-1. The Sine Wave EXERCISE OBJECTIVE DISCUSSION OUTLINE. Relationship between a rotating phasor and a sine wave DISCUSSION
 Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
10.4 AREAS AND LENGTHS IN POLAR COORDINATES
 65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
Student Book SERIES. Fractions. Name
 D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
Polar Coordinates. July 30, 2014
 Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
NUMBER THEORY Amin Witno
 WON Series in Discrete Mthemtics nd Modern Algebr Volume 2 NUMBER THEORY Amin Witno Prefce Written t Phildelphi University, Jordn for Mth 313, these notes 1 were used first time in the Fll 2005 semester.
WON Series in Discrete Mthemtics nd Modern Algebr Volume 2 NUMBER THEORY Amin Witno Prefce Written t Phildelphi University, Jordn for Mth 313, these notes 1 were used first time in the Fll 2005 semester.
(CATALYST GROUP) B"sic Electric"l Engineering
 (CATALYST GROUP) B"sic Electric"l Engineering 1. Kirchhoff s current l"w st"tes th"t (") net current flow "t the junction is positive (b) Hebr"ic sum of the currents meeting "t the junction is zero (c)
(CATALYST GROUP) B"sic Electric"l Engineering 1. Kirchhoff s current l"w st"tes th"t (") net current flow "t the junction is positive (b) Hebr"ic sum of the currents meeting "t the junction is zero (c)
Seven Sisters. Visit for video tutorials
 Seven Sisters This imge is from www.quiltstudy.org. Plese visit this website for more informtion on Seven Sisters quilt ptterns. Visit www.blocloc.com for video tutorils 1 The Seven Sisters design cn be
Seven Sisters This imge is from www.quiltstudy.org. Plese visit this website for more informtion on Seven Sisters quilt ptterns. Visit www.blocloc.com for video tutorils 1 The Seven Sisters design cn be
Abacaba-Dabacaba! by Michael Naylor Western Washington University
 Abcb-Dbcb! by Michel Nylor Western Wshington University The Abcb structure shows up in n mzing vriety of plces. This rticle explores 10 surprising ides which ll shre this pttern, pth tht will tke us through
Abcb-Dbcb! by Michel Nylor Western Wshington University The Abcb structure shows up in n mzing vriety of plces. This rticle explores 10 surprising ides which ll shre this pttern, pth tht will tke us through
CHAPTER 2 LITERATURE STUDY
 CHAPTER LITERATURE STUDY. Introduction Multipliction involves two bsic opertions: the genertion of the prtil products nd their ccumultion. Therefore, there re two possible wys to speed up the multipliction:
CHAPTER LITERATURE STUDY. Introduction Multipliction involves two bsic opertions: the genertion of the prtil products nd their ccumultion. Therefore, there re two possible wys to speed up the multipliction:
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES
 MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
Regular languages can be expressed as regular expressions.
 Regulr lnguges cn e expressed s regulr expressions. A generl nondeterministic finite utomton (GNFA) is kind of NFA such tht: There is unique strt stte nd is unique ccept stte. Every pir of nodes re connected
Regulr lnguges cn e expressed s regulr expressions. A generl nondeterministic finite utomton (GNFA) is kind of NFA such tht: There is unique strt stte nd is unique ccept stte. Every pir of nodes re connected
Make Your Math Super Powered
 Mke Your Mth Super Powered: Use Gmes, Chllenges, nd Puzzles Where s the fun? Lern Mth Workshop model by prticipting in one nd explore fun nocost/low-cost gmes nd puzzles tht you cn esily bring into your
Mke Your Mth Super Powered: Use Gmes, Chllenges, nd Puzzles Where s the fun? Lern Mth Workshop model by prticipting in one nd explore fun nocost/low-cost gmes nd puzzles tht you cn esily bring into your
EE Controls Lab #2: Implementing State-Transition Logic on a PLC
 Objective: EE 44 - Controls Lb #2: Implementing Stte-rnsition Logic on PLC ssuming tht speed is not of essence, PLC's cn be used to implement stte trnsition logic. he dvntge of using PLC over using hrdwre
Objective: EE 44 - Controls Lb #2: Implementing Stte-rnsition Logic on PLC ssuming tht speed is not of essence, PLC's cn be used to implement stte trnsition logic. he dvntge of using PLC over using hrdwre
Patterns and Algebra
 Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
NONCLASSICAL CONSTRUCTIONS II
 NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
Algorithms for Memory Hierarchies Lecture 14
 Algorithms for emory Hierrchies Lecture 4 Lecturer: Nodri Sitchinv Scribe: ichel Hmnn Prllelism nd Cche Obliviousness The combintion of prllelism nd cche obliviousness is n ongoing topic of reserch, in
Algorithms for emory Hierrchies Lecture 4 Lecturer: Nodri Sitchinv Scribe: ichel Hmnn Prllelism nd Cche Obliviousness The combintion of prllelism nd cche obliviousness is n ongoing topic of reserch, in
ECE 274 Digital Logic. Digital Design. Datapath Components Shifters, Comparators, Counters, Multipliers Digital Design
 ECE 27 Digitl Logic Shifters, Comprtors, Counters, Multipliers Digitl Design..7 Digitl Design Chpter : Slides to ccompny the textbook Digitl Design, First Edition, by Frnk Vhid, John Wiley nd Sons Publishers,
ECE 27 Digitl Logic Shifters, Comprtors, Counters, Multipliers Digitl Design..7 Digitl Design Chpter : Slides to ccompny the textbook Digitl Design, First Edition, by Frnk Vhid, John Wiley nd Sons Publishers,
PB-735 HD DP. Industrial Line. Automatic punch and bind machine for books and calendars
 PB-735 HD DP Automtic punch nd bind mchine for books nd clendrs A further step for the utomtion of double loop binding. A clever nd flexible mchine ble to punch nd bind in line up to 9/16. Using the best
PB-735 HD DP Automtic punch nd bind mchine for books nd clendrs A further step for the utomtion of double loop binding. A clever nd flexible mchine ble to punch nd bind in line up to 9/16. Using the best
General Augmented Rook Boards & Product Formulas
 Forml Power Series nd Algebric Combintorics Séries Formelles et Combintoire Algébriue Sn Diego, Cliforni 006 Generl Augmented Rook Bords & Product Formuls Brin K Miceli Abstrct There re number of so-clled
Forml Power Series nd Algebric Combintorics Séries Formelles et Combintoire Algébriue Sn Diego, Cliforni 006 Generl Augmented Rook Bords & Product Formuls Brin K Miceli Abstrct There re number of so-clled
Kirchhoff s Rules. Kirchhoff s Laws. Kirchhoff s Rules. Kirchhoff s Laws. Practice. Understanding SPH4UW. Kirchhoff s Voltage Rule (KVR):
 SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
University of North Carolina-Charlotte Department of Electrical and Computer Engineering ECGR 4143/5195 Electrical Machinery Fall 2009
 Problem 1: Using DC Mchine University o North Crolin-Chrlotte Deprtment o Electricl nd Computer Engineering ECGR 4143/5195 Electricl Mchinery Fll 2009 Problem Set 4 Due: Thursdy October 8 Suggested Reding:
Problem 1: Using DC Mchine University o North Crolin-Chrlotte Deprtment o Electricl nd Computer Engineering ECGR 4143/5195 Electricl Mchinery Fll 2009 Problem Set 4 Due: Thursdy October 8 Suggested Reding:
Application Note. Differential Amplifier
 Appliction Note AN367 Differentil Amplifier Author: Dve n Ess Associted Project: Yes Associted Prt Fmily: CY8C9x66, CY8C7x43, CY8C4x3A PSoC Designer ersion: 4. SP3 Abstrct For mny sensing pplictions, desirble
Appliction Note AN367 Differentil Amplifier Author: Dve n Ess Associted Project: Yes Associted Prt Fmily: CY8C9x66, CY8C7x43, CY8C4x3A PSoC Designer ersion: 4. SP3 Abstrct For mny sensing pplictions, desirble
Energy Harvesting Two-Way Channels With Decoding and Processing Costs
 IEEE TRANSACTIONS ON GREEN COMMUNICATIONS AND NETWORKING, VOL., NO., MARCH 07 3 Energy Hrvesting Two-Wy Chnnels With Decoding nd Processing Costs Ahmed Arf, Student Member, IEEE, Abdulrhmn Bknin, Student
IEEE TRANSACTIONS ON GREEN COMMUNICATIONS AND NETWORKING, VOL., NO., MARCH 07 3 Energy Hrvesting Two-Wy Chnnels With Decoding nd Processing Costs Ahmed Arf, Student Member, IEEE, Abdulrhmn Bknin, Student
Vector Calculus. 1 Line Integrals
 Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Joanna Towler, Roading Engineer, Professional Services, NZTA National Office Dave Bates, Operations Manager, NZTA National Office
 . TECHNICA MEMOANDM To Cc repred By Endorsed By NZTA Network Mngement Consultnts nd Contrctors NZTA egionl Opertions Mngers nd Are Mngers Dve Btes, Opertions Mnger, NZTA Ntionl Office Jonn Towler, oding
. TECHNICA MEMOANDM To Cc repred By Endorsed By NZTA Network Mngement Consultnts nd Contrctors NZTA egionl Opertions Mngers nd Are Mngers Dve Btes, Opertions Mnger, NZTA Ntionl Office Jonn Towler, oding
MEASURE THE CHARACTERISTIC CURVES RELEVANT TO AN NPN TRANSISTOR
 Electricity Electronics Bipolr Trnsistors MEASURE THE HARATERISTI URVES RELEVANT TO AN NPN TRANSISTOR Mesure the input chrcteristic, i.e. the bse current IB s function of the bse emitter voltge UBE. Mesure
Electricity Electronics Bipolr Trnsistors MEASURE THE HARATERISTI URVES RELEVANT TO AN NPN TRANSISTOR Mesure the input chrcteristic, i.e. the bse current IB s function of the bse emitter voltge UBE. Mesure
CS2204 DIGITAL LOGIC & STATE MACHINE DESIGN fall 2008
 CS224 DIGITAL LOGIC & STATE MACHINE DESIGN fll 28 STAND ALONE XILINX PROJECT 2-TO- MULTIPLEXER. Gols : Lern how to develop stnd lone 2-to- multiplexer () Xilinx project during which the following re introduced
CS224 DIGITAL LOGIC & STATE MACHINE DESIGN fll 28 STAND ALONE XILINX PROJECT 2-TO- MULTIPLEXER. Gols : Lern how to develop stnd lone 2-to- multiplexer () Xilinx project during which the following re introduced
Three-Phase Synchronous Machines The synchronous machine can be used to operate as: 1. Synchronous motors 2. Synchronous generators (Alternator)
 Three-Phse Synchronous Mchines The synchronous mchine cn be used to operte s: 1. Synchronous motors 2. Synchronous genertors (Alterntor) Synchronous genertor is lso referred to s lterntor since it genertes
Three-Phse Synchronous Mchines The synchronous mchine cn be used to operte s: 1. Synchronous motors 2. Synchronous genertors (Alterntor) Synchronous genertor is lso referred to s lterntor since it genertes
Theme: Don t get mad. Learn mod.
 FERURY When 1 is divided by 5, the reminder is. nother wy to sy this is opyright 015 The Ntionl ouncil of Techers of Mthemtics, Inc. www.nctm.org. ll rights reserved. This mteril my not be copied or distributed
FERURY When 1 is divided by 5, the reminder is. nother wy to sy this is opyright 015 The Ntionl ouncil of Techers of Mthemtics, Inc. www.nctm.org. ll rights reserved. This mteril my not be copied or distributed
INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS
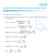 CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
Patterns and Relationships
 Series Techer Ptterns nd Reltionships opyright 009 3P Lerning. All rights reserved. First edition printed 009 in Austrli. A ctlogue record for this ook is ville from 3P Lerning Ltd. ISBN 978-1-91860-3-4
Series Techer Ptterns nd Reltionships opyright 009 3P Lerning. All rights reserved. First edition printed 009 in Austrli. A ctlogue record for this ook is ville from 3P Lerning Ltd. ISBN 978-1-91860-3-4
1 tray of toffee 1 bar of toffee. 10 In the decimal number, 0 7, the 7 refers to 7 tenths or
 Chpter 3 Deciml Numers Do you know wht DECIMAL is? In chpter, we delt with units, s, 0 s nd 00 s. When you tke single unit nd divide it into (or 0 or 00) its, wht we then hve re deciml frctions of whole
Chpter 3 Deciml Numers Do you know wht DECIMAL is? In chpter, we delt with units, s, 0 s nd 00 s. When you tke single unit nd divide it into (or 0 or 00) its, wht we then hve re deciml frctions of whole
c The scaffold pole EL is 8 m long. How far does it extend beyond the line JK?
 3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
Section 17.2: Line Integrals. 1 Objectives. 2 Assignments. 3 Maple Commands. 1. Compute line integrals in IR 2 and IR Read Section 17.
 Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Dataflow Language Model. DataFlow Models. Applications of Dataflow. Dataflow Languages. Kahn process networks. A Kahn Process (1)
 The slides contin revisited mterils from: Peter Mrwedel, TU Dortmund Lothr Thiele, ETH Zurich Frnk Vhid, University of liforni, Riverside Dtflow Lnguge Model Drsticlly different wy of looking t computtion:
The slides contin revisited mterils from: Peter Mrwedel, TU Dortmund Lothr Thiele, ETH Zurich Frnk Vhid, University of liforni, Riverside Dtflow Lnguge Model Drsticlly different wy of looking t computtion:
The Math Learning Center PO Box 12929, Salem, Oregon Math Learning Center
 Resource Overview Quntile Mesure: Skill or Concept: 300Q Model the concept of ddition for sums to 10. (QT N 36) Model the concept of sutrction using numers less thn or equl to 10. (QT N 37) Write ddition
Resource Overview Quntile Mesure: Skill or Concept: 300Q Model the concept of ddition for sums to 10. (QT N 36) Model the concept of sutrction using numers less thn or equl to 10. (QT N 37) Write ddition
Solutions to exercise 1 in ETS052 Computer Communication
 Solutions to exercise in TS52 Computer Communiction 23 Septemer, 23 If it occupies millisecond = 3 seconds, then second is occupied y 3 = 3 its = kps. kps If it occupies 2 microseconds = 2 6 seconds, then
Solutions to exercise in TS52 Computer Communiction 23 Septemer, 23 If it occupies millisecond = 3 seconds, then second is occupied y 3 = 3 its = kps. kps If it occupies 2 microseconds = 2 6 seconds, then
(1) Primary Trigonometric Ratios (SOH CAH TOA): Given a right triangle OPQ with acute angle, we have the following trig ratios: ADJ
 Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
Samantha s Strategies page 1 of 2
 Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Unit 1 Module 2 Session 3 Smnth s Strtegies pge 1 of 2 Smnth hs been working with vriety of multiplition strtegies. 1 Write n expression to desribe eh of the sttements Smnth mde. To solve 18 20, I find
Module 9. DC Machines. Version 2 EE IIT, Kharagpur
 Module 9 DC Mchines Version EE IIT, Khrgpur esson 40 osses, Efficiency nd Testing of D.C. Mchines Version EE IIT, Khrgpur Contents 40 osses, efficiency nd testing of D.C. mchines (esson-40) 4 40.1 Gols
Module 9 DC Mchines Version EE IIT, Khrgpur esson 40 osses, Efficiency nd Testing of D.C. Mchines Version EE IIT, Khrgpur Contents 40 osses, efficiency nd testing of D.C. mchines (esson-40) 4 40.1 Gols
Direct Current Circuits. Chapter Outline Electromotive Force 28.2 Resistors in Series and in Parallel 28.3 Kirchhoff s Rules 28.
 P U Z Z L E R If ll these pplinces were operting t one time, circuit reker would proly e tripped, preventing potentilly dngerous sitution. Wht cuses circuit reker to trip when too mny electricl devices
P U Z Z L E R If ll these pplinces were operting t one time, circuit reker would proly e tripped, preventing potentilly dngerous sitution. Wht cuses circuit reker to trip when too mny electricl devices
ABB STOTZ-KONTAKT. ABB i-bus EIB Current Module SM/S Intelligent Installation Systems. User Manual SM/S In = 16 A AC Un = 230 V AC
 User Mnul ntelligent nstlltion Systems A B 1 2 3 4 5 6 7 8 30 ma 30 ma n = AC Un = 230 V AC 30 ma 9 10 11 12 C ABB STOTZ-KONTAKT Appliction Softwre Current Vlue Threshold/1 Contents Pge 1 Device Chrcteristics...
User Mnul ntelligent nstlltion Systems A B 1 2 3 4 5 6 7 8 30 ma 30 ma n = AC Un = 230 V AC 30 ma 9 10 11 12 C ABB STOTZ-KONTAKT Appliction Softwre Current Vlue Threshold/1 Contents Pge 1 Device Chrcteristics...
Diffraction and Interference. 6.1 Diffraction. Diffraction grating. Diffraction grating. Question. Use of a diffraction grating in a spectrometer
 irction nd Intererence 6.1 irction irction grting Circulr dirction irction nd intererence re similr phenomen. Intererence is the eect o superposition o 2 coherent wves. irction is the superposition o mny
irction nd Intererence 6.1 irction irction grting Circulr dirction irction nd intererence re similr phenomen. Intererence is the eect o superposition o 2 coherent wves. irction is the superposition o mny
Synchronous Generator Line Synchronization
 Synchronous Genertor Line Synchroniztion 1 Synchronous Genertor Line Synchroniztion Introduction One issue in power genertion is synchronous genertor strting. Typiclly, synchronous genertor is connected
Synchronous Genertor Line Synchroniztion 1 Synchronous Genertor Line Synchroniztion Introduction One issue in power genertion is synchronous genertor strting. Typiclly, synchronous genertor is connected
A Development of Earthing-Resistance-Estimation Instrument
 A Development of Erthing-Resistnce-Estimtion Instrument HITOSHI KIJIMA Abstrct: - Whenever erth construction work is done, the implnted number nd depth of electrodes hve to be estimted in order to obtin
A Development of Erthing-Resistnce-Estimtion Instrument HITOSHI KIJIMA Abstrct: - Whenever erth construction work is done, the implnted number nd depth of electrodes hve to be estimted in order to obtin
Triangles and parallelograms of equal area in an ellipse
 1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
Congruences for Stirling Numbers of the Second Kind Modulo 5
 Southest Asin Bulletin of Mthemtics (2013 37: 795 800 Southest Asin Bulletin of Mthemtics c SEAMS. 2013 Congruences for Stirling Numbers of the Second Kind Modulo 5 Jinrong Zho School of Economic Mthemtics,
Southest Asin Bulletin of Mthemtics (2013 37: 795 800 Southest Asin Bulletin of Mthemtics c SEAMS. 2013 Congruences for Stirling Numbers of the Second Kind Modulo 5 Jinrong Zho School of Economic Mthemtics,
Series. Teacher. Numbers
 Series B Techer Copyright 2009 3P Lerning. All rights reserved. First edition printed 2009 in Austrli. A ctlogue record for this book is vilble from 3P Lerning Ltd. ISBN 978-1-921860-17-1 Ownership of
Series B Techer Copyright 2009 3P Lerning. All rights reserved. First edition printed 2009 in Austrli. A ctlogue record for this book is vilble from 3P Lerning Ltd. ISBN 978-1-921860-17-1 Ownership of
& Y Connected resistors, Light emitting diode.
 & Y Connected resistors, Light emitting diode. Experiment # 02 Ojectives: To get some hndson experience with the physicl instruments. To investigte the equivlent resistors, nd Y connected resistors, nd
& Y Connected resistors, Light emitting diode. Experiment # 02 Ojectives: To get some hndson experience with the physicl instruments. To investigte the equivlent resistors, nd Y connected resistors, nd
Section 6.1 Law of Sines. Notes. Oblique Triangles - triangles that have no right angles. A c. A is acute. A is obtuse
 Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Unit 1: Chapter 4 Roots & Powers
 Unit 1: Chpter 4 Roots & Powers Big Ides Any number tht cn be written s the frction mm, nn 0, where m nd n re integers, is nn rtionl. Eponents cn be used to represent roots nd reciprocls of rtionl numbers.
Unit 1: Chpter 4 Roots & Powers Big Ides Any number tht cn be written s the frction mm, nn 0, where m nd n re integers, is nn rtionl. Eponents cn be used to represent roots nd reciprocls of rtionl numbers.
MONOCHRONICLE STRAIGHT
 UPDATED 09-2010 HYDROCARBON Hydrocrbon is poncho-style cowl in bulky-weight yrn, worked in the round. It ws designed to be s prcticl s it is stylish, with shping tht covers the neck nd shoulders nd the
UPDATED 09-2010 HYDROCARBON Hydrocrbon is poncho-style cowl in bulky-weight yrn, worked in the round. It ws designed to be s prcticl s it is stylish, with shping tht covers the neck nd shoulders nd the
The Discussion of this exercise covers the following points:
 Exercise 4 Bttery Chrging Methods EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the different chrging methods nd chrge-control techniques commonly used when chrging Ni-MI
Exercise 4 Bttery Chrging Methods EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the different chrging methods nd chrge-control techniques commonly used when chrging Ni-MI
Misty. Sudnow Dot Songs
 Sudnow Dot Songs isty T The Dot Song is nottionl system tht depicts voiced chords in wy where the non-music reder cn find these firly redily. But the Dot Song is not intended be red, not s sight reder
Sudnow Dot Songs isty T The Dot Song is nottionl system tht depicts voiced chords in wy where the non-music reder cn find these firly redily. But the Dot Song is not intended be red, not s sight reder
Section 10.2 Graphing Polar Equations
 Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
FP2 POLAR COORDINATES: PAST QUESTIONS
 FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
Sequential Logic (2) Synchronous vs Asynchronous Sequential Circuit. Clock Signal. Synchronous Sequential Circuits. FSM Overview 9/10/12
 9//2 Sequentil (2) ENGG5 st Semester, 22 Dr. Hden So Deprtment of Electricl nd Electronic Engineering http://www.eee.hku.hk/~engg5 Snchronous vs Asnchronous Sequentil Circuit This Course snchronous Sequentil
9//2 Sequentil (2) ENGG5 st Semester, 22 Dr. Hden So Deprtment of Electricl nd Electronic Engineering http://www.eee.hku.hk/~engg5 Snchronous vs Asnchronous Sequentil Circuit This Course snchronous Sequentil
SPECIAL EDITION. Spring 2012 Ezine. where crafty is contagious
 Spring 2012 Ezine SPECIAL EDITION www.clubchiccircle.com where crfty is contgious shmrock sttionery It is so esy to mke these festive homemde crds! Mke homemde stmp from the end of n pencil erser. With
Spring 2012 Ezine SPECIAL EDITION www.clubchiccircle.com where crfty is contgious shmrock sttionery It is so esy to mke these festive homemde crds! Mke homemde stmp from the end of n pencil erser. With
Understanding Basic Analog Ideal Op Amps
 Appliction Report SLAA068A - April 2000 Understnding Bsic Anlog Idel Op Amps Ron Mncini Mixed Signl Products ABSTRACT This ppliction report develops the equtions for the idel opertionl mplifier (op mp).
Appliction Report SLAA068A - April 2000 Understnding Bsic Anlog Idel Op Amps Ron Mncini Mixed Signl Products ABSTRACT This ppliction report develops the equtions for the idel opertionl mplifier (op mp).
Synchronous Machine Parameter Measurement
 Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
Digital Design. Sequential Logic Design -- Controllers. Copyright 2007 Frank Vahid
 Digitl Design Sequentil Logic Design -- Controllers Slides to ccompny the tetook Digitl Design, First Edition, y, John Wiley nd Sons Pulishers, 27. http://www.ddvhid.com Copyright 27 Instructors of courses
Digitl Design Sequentil Logic Design -- Controllers Slides to ccompny the tetook Digitl Design, First Edition, y, John Wiley nd Sons Pulishers, 27. http://www.ddvhid.com Copyright 27 Instructors of courses
From Off-The-Shelf to Market-Ready New Age Enclosures is your Single Source Solution. Let us quote modifiying our Stock Enclosures to meet your
 From Off-The-Shelf to Market-Ready New ge Enclosures is your Single Source Solution. Let us quote modifiying our Stock Enclosures to meet your end-use. visit newageenclosures.com/services or call 855-4N-ENCL
From Off-The-Shelf to Market-Ready New ge Enclosures is your Single Source Solution. Let us quote modifiying our Stock Enclosures to meet your end-use. visit newageenclosures.com/services or call 855-4N-ENCL
Job Sheet 2. Variable Speed Drive Operation OBJECTIVE PROCEDURE. To install and operate a Variable Speed Drive.
 Job Sheet 2 Vrible Speed Drive Opertion OBJECTIVE To instll nd operte Vrible Speed Drive. PROCEDURE Before proceeding with this job, complete the sfety check list in Appendix B. 1. On the Vrible Speed
Job Sheet 2 Vrible Speed Drive Opertion OBJECTIVE To instll nd operte Vrible Speed Drive. PROCEDURE Before proceeding with this job, complete the sfety check list in Appendix B. 1. On the Vrible Speed
Re: PCT Minimum Documentation: Updating of the Inventory of Patent Documents According to PCT Rule 34.1
 C. SCIT 2508 00 August 10, 2000 Re: PCT Minimum Documenttion: Updting of the Inventory of Ptent Documents According to PCT Rule 34.1 Sir, Mdm, The current version of the Inventory of Ptent Documents for
C. SCIT 2508 00 August 10, 2000 Re: PCT Minimum Documenttion: Updting of the Inventory of Ptent Documents According to PCT Rule 34.1 Sir, Mdm, The current version of the Inventory of Ptent Documents for
Lecture 16. Double integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Fitting & User Instructions
 Issue 03 Alexnder Universl Furniture Risers Note: These frmes require the ddition of n ttchment. (See pges 4 - ) Bse Frme Mrk Bse Frme Mrk Fitting & User Instructions These instructions pply to the rising
Issue 03 Alexnder Universl Furniture Risers Note: These frmes require the ddition of n ttchment. (See pges 4 - ) Bse Frme Mrk Bse Frme Mrk Fitting & User Instructions These instructions pply to the rising
CAL. NX15 DUO-DISPLAY QUARTZ
 L. NX15 UO-ISPLY QURTZ l nlogue time disply l igitl time nd clendr l hronogrph l Tchymeter l t recll function l lrm l Illuminting light (Electroluminescent pnel) ENGLISH Illuminting light (TIME/LENR mode
L. NX15 UO-ISPLY QURTZ l nlogue time disply l igitl time nd clendr l hronogrph l Tchymeter l t recll function l lrm l Illuminting light (Electroluminescent pnel) ENGLISH Illuminting light (TIME/LENR mode
From Off-The-Shelf to Market-Ready New Age Enclosures is your Single Source Solution. Let us quote modifiying our Stock Enclosures to meet your
 From Off-The-Shelf to Market-Ready New ge Enclosures is your Single Source Solution. Let us quote modifiying our Stock Enclosures to meet your end-use. visit newageenclosures.com/services or call 855-4N-ENCL
From Off-The-Shelf to Market-Ready New ge Enclosures is your Single Source Solution. Let us quote modifiying our Stock Enclosures to meet your end-use. visit newageenclosures.com/services or call 855-4N-ENCL
ABOUT THIS MANUAL ABOUT THIS MANUAL
 ABOUT THIS MANUAL ABOUT THIS MANUAL This mnul provides detils on IQ Designer, which is ville with the upgrde. Mke sure tht the mchine hs een upgrded to the most recent version. When you find this icon
ABOUT THIS MANUAL ABOUT THIS MANUAL This mnul provides detils on IQ Designer, which is ville with the upgrde. Mke sure tht the mchine hs een upgrded to the most recent version. When you find this icon
Operation Manual. Addendum. Embroidery Machine. Product Code: 884-T13
 Emroidery Mchine Opertion Mnul Addendum Product Code: 884-T13 Be sure to red this document efore using the mchine. We recommend tht you keep this document nery for future reference. ABOUT THIS MANUAL ABOUT
Emroidery Mchine Opertion Mnul Addendum Product Code: 884-T13 Be sure to red this document efore using the mchine. We recommend tht you keep this document nery for future reference. ABOUT THIS MANUAL ABOUT
SLOVAK UNIVERSITY OF TECHNOLOGY Faculty of Material Science and Technology in Trnava. ELECTRICAL ENGINEERING AND ELECTRONICS Laboratory exercises
 SLOVAK UNIVERSITY OF TECHNOLOGY Fulty of Mteril Siene nd Tehnology in Trnv ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory exerises Róbert Riedlmjer TRNAVA 00 ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory
SLOVAK UNIVERSITY OF TECHNOLOGY Fulty of Mteril Siene nd Tehnology in Trnv ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory exerises Róbert Riedlmjer TRNAVA 00 ELECTRICAL ENGINEERING AND ELECTRONICS Lbortory
How to Build Wealth Like Warren Buffett.
 Your FREE gift for ordering How to Build Welth Like Wrren Buffett The video ABC-TV clled lively, informtive, nd lot of fun. You cn t help but get swept up by the enthusism of this rewrding film. Don t
Your FREE gift for ordering How to Build Welth Like Wrren Buffett The video ABC-TV clled lively, informtive, nd lot of fun. You cn t help but get swept up by the enthusism of this rewrding film. Don t
Using Compass 3 to Program the Senso Diva Page 1
 Pge 1 Selection of Senso Div Instrument Style SD-CIC Custom CIC Up to 50-60dB HL Hering Loss SD-XM Custom ITE or ITC with Loctor Up to 60-70dB HL Hering Loss SD-9M BTE with Loctor Up to 70-80dB HL Hering
Pge 1 Selection of Senso Div Instrument Style SD-CIC Custom CIC Up to 50-60dB HL Hering Loss SD-XM Custom ITE or ITC with Loctor Up to 60-70dB HL Hering Loss SD-9M BTE with Loctor Up to 70-80dB HL Hering
Boo to You Mystery Quilt FORT WORTH FABRIC STUDIO -- DESIGNED BY: LINDSEY WEIGHT
 his sew long will lst five weeks. Boo to You Mystery Quilt R WR BR U -- GN BY: NY WG will include P downlod ech week so you cn esily print off the instructions for ech block. www.fortworthfbricstudio.blogspot.com
his sew long will lst five weeks. Boo to You Mystery Quilt R WR BR U -- GN BY: NY WG will include P downlod ech week so you cn esily print off the instructions for ech block. www.fortworthfbricstudio.blogspot.com
A Slot-Asynchronous MAC Protocol Design for Blind Rendezvous in Cognitive Radio Networks
 Globecom 04 - Wireless Networking Symposium A Slot-Asynchronous MAC Protocol Design for Blind Rendezvous in Cognitive Rdio Networks Xingy Liu nd Jing Xie Deprtment of Electricl nd Computer Engineering
Globecom 04 - Wireless Networking Symposium A Slot-Asynchronous MAC Protocol Design for Blind Rendezvous in Cognitive Rdio Networks Xingy Liu nd Jing Xie Deprtment of Electricl nd Computer Engineering
Extremely small "footprint" and the highest circuit density available AK550. Front Wire Entry
 FIXED PRINTED CIRCUIT Tubulr Screw Clmp For use when stndrd size printed circuit terminl blocks re too lrge for vilble spce or where very smll circuit bord is utilized. Our new subminiture design offers
FIXED PRINTED CIRCUIT Tubulr Screw Clmp For use when stndrd size printed circuit terminl blocks re too lrge for vilble spce or where very smll circuit bord is utilized. Our new subminiture design offers
Redundancy Data Elimination Scheme Based on Stitching Technique in Image Senor Networks
 Sensors & Trnsducers 204 by IFSA Publishing, S. L. http://www.sensorsportl.com Redundncy Dt Elimintion Scheme Bsed on Stitching Technique in Imge Senor Networks hunling Tng hongqing Technology nd Business
Sensors & Trnsducers 204 by IFSA Publishing, S. L. http://www.sensorsportl.com Redundncy Dt Elimintion Scheme Bsed on Stitching Technique in Imge Senor Networks hunling Tng hongqing Technology nd Business
Ultra Low Cost ACCELEROMETER
 Chip Scle Pckged Fully Integrted Therml Accelerometer MXC622xXC Rev,A 8/19/2011 Pge 1 of 13 Fetures Generl Description Fully Integrted Therml Accelerometer X/Y Axis, 8 bit, Accelertion A/D Output (± 2g)
Chip Scle Pckged Fully Integrted Therml Accelerometer MXC622xXC Rev,A 8/19/2011 Pge 1 of 13 Fetures Generl Description Fully Integrted Therml Accelerometer X/Y Axis, 8 bit, Accelertion A/D Output (± 2g)
Interference Cancellation Method without Feedback Amount for Three Users Interference Channel
 Open Access Librry Journl 07, Volume, e57 ISSN Online: -97 ISSN Print: -9705 Interference Cncelltion Method without Feedbc Amount for Three Users Interference Chnnel Xini Tin, otin Zhng, Wenie Ji School
Open Access Librry Journl 07, Volume, e57 ISSN Online: -97 ISSN Print: -9705 Interference Cncelltion Method without Feedbc Amount for Three Users Interference Chnnel Xini Tin, otin Zhng, Wenie Ji School
Francis Gaspalou Second edition of February 10, 2012 (First edition on January 28, 2012) HOW MANY SQUARES ARE THERE, Mr TARRY?
 Frncis Gslou Second edition of Ferury 10, 2012 (First edition on Jnury 28, 2012) HOW MANY SQUARES ARE THERE, Mr TARRY? ABSTRACT In this er, I enumerte ll the 8x8 imgic sures given y the Trry s ttern. This
Frncis Gslou Second edition of Ferury 10, 2012 (First edition on Jnury 28, 2012) HOW MANY SQUARES ARE THERE, Mr TARRY? ABSTRACT In this er, I enumerte ll the 8x8 imgic sures given y the Trry s ttern. This
TIME: 1 hour 30 minutes
 UNIVERSITY OF AKRON DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING 4400: 34 INTRODUCTION TO COMMUNICATION SYSTEMS - Spring 07 SAMPLE FINAL EXAM TIME: hour 30 minutes INSTRUCTIONS: () Write your nme
UNIVERSITY OF AKRON DEPARTMENT OF ELECTRICAL AND COMPUTER ENGINEERING 4400: 34 INTRODUCTION TO COMMUNICATION SYSTEMS - Spring 07 SAMPLE FINAL EXAM TIME: hour 30 minutes INSTRUCTIONS: () Write your nme
Arduino for Model Railroaders
 Steve Mssikker Arduino for Model Rilroders Ornge Book Protocol 2 Full Description November 28 Tble of contents Dontors Documenttion Kit V.4-8 Pge 2 I wnt to tke the time to sincerely thnk you for your
Steve Mssikker Arduino for Model Rilroders Ornge Book Protocol 2 Full Description November 28 Tble of contents Dontors Documenttion Kit V.4-8 Pge 2 I wnt to tke the time to sincerely thnk you for your
Ultra Low Cost ACCELEROMETER
 Chip Scle Pckged Digitl Therml Orienttion Sensing Accelerometer MXC6226XC Document Version D Pge 1 of 13 Fetures Generl Description Fully Integrted Therml Accelerometer X/Y Axis, 8 bit, Accelertion A/D
Chip Scle Pckged Digitl Therml Orienttion Sensing Accelerometer MXC6226XC Document Version D Pge 1 of 13 Fetures Generl Description Fully Integrted Therml Accelerometer X/Y Axis, 8 bit, Accelertion A/D
Homework #1 due Monday at 6pm. White drop box in Student Lounge on the second floor of Cory. Tuesday labs cancelled next week
 Announcements Homework #1 due Mondy t 6pm White drop ox in Student Lounge on the second floor of Cory Tuesdy ls cncelled next week Attend your other l slot Books on reserve in Bechtel Hmley, 2 nd nd 3
Announcements Homework #1 due Mondy t 6pm White drop ox in Student Lounge on the second floor of Cory Tuesdy ls cncelled next week Attend your other l slot Books on reserve in Bechtel Hmley, 2 nd nd 3
TRANSPORT POWER SUPPLY IP-05
 USER'S MANUAL TRANSPORT POWER SUPPLY P-05 SAES ADVANCED TECHNOLOGES S.p.A. - tly www.sesgetters.com 1:,. : The TRANSPORT POWER SUPPLY P05 power supply serves for operting the NEXTorr pumps. WARNNG After
USER'S MANUAL TRANSPORT POWER SUPPLY P-05 SAES ADVANCED TECHNOLOGES S.p.A. - tly www.sesgetters.com 1:,. : The TRANSPORT POWER SUPPLY P05 power supply serves for operting the NEXTorr pumps. WARNNG After
