Updated December Year. Small Steps Guidance and Examples. Block 4: Multiplication & Division
|
|
|
- Lydia McDowell
- 6 years ago
- Views:
Transcription
1 Updated December 2017 Year 5 Small Steps Guidance and Examples Block 4: Multiplication & Division
2 Year 5 Autumn Term Teaching Guidance Multiples Notes and Guidance Building on their times tables knowledge, children will find multiples of whole numbers. Children build multiples of a number using concrete and pictorial representations e.g. in an array. Mathematical Talk What do you notice about the multiples of 2? What is the same about them, what is different? Look at multiples of other numbers; is there a rule that links them? Circle the multiples of What do you notice about the multiples of 5?. Write all the multiples of 4 between 20 and 80. Roll 2 die (1-6), multiply the numbers. What is the number a multiple of? Is it a multiple of more than one number? How many different numbers can you make multiples of? Can you make multiples of all numbers up to 10? Can you make multiples of all numbers up to 20? Use a table to show your results. Multiply the numbers you roll to complete the table. An example is shown below
3 Year 5 Autumn Term Multiples Reasoning and Problem Solving Use the digits 0 9. Choose 2 digits. Multiply them together. What is your number a multiple of? Is it a multiple of more than one number? Can you find all the numbers you could make? Use the table below to help Always, Sometimes, Never The product of two even numbers is a multiple of an odd number. The product of two odd numbers is a multiple of an even number. Clare s age is a multiple of 7 and is 3 less than a multiple of 8. She is younger than 40. How old is Clare? Always- Two even numbers multiplied together are all multiples of 1. Never- Two odd numbers multiplied together are always a multiple of an odd number. You cannot make a multiple of an even number. Clare is 21 years old,
4 Year 5 Autumn Term Teaching Guidance Factors Notes and Guidance Children understand the relationship between multiplication and division and can use arrays to show the relationship between them. They know that division means sharing and finding equal groups of amounts. Children learn that a factor of a number is the number you get when you divide a whole number by another whole number and that factors come in pairs. (factor factor = product). Mathematical Talk How can work in a systematic way to prove you have found all the factors? Do factors always come in pairs? How can we use our multiplication and division facts to find factors? If you have twenty counters, how many different ways of arranging them can you find? How many factors of twenty have you found? E.g. A pair of factors of 20 are 4 and Circle the factors of 60 9, 6, 8, 4, 12, 5, 60, 15, 45, Which factors of 60 are not shown? Fill in the missing factors of What do you notice about the order of the factors? Use this method to find the factors of 42
5 Year 5 Autumn Term Factors Reasoning and Problem Solving Here is Kayla s method for finding factor pairs: X 6 6 Use Kayla s method to find the factors of 64 When do you put a cross next to a number? What do you do if a number appears twice? To find the factors of a number, you have to find all the pairs of numbers that multiply together to give that number. Factors of 12 = 1, 2, 3, 4, 6, 12 If we leave the number we started with (12) and add all the other factors together we get is called an abundant number because 12 is less than the sum of its factors. How many abundant numbers can you find between 1-40? Start with the number 1 and work systematically to 40. Sometimes, Always, Never: An even number has an even amount of factors Sometimes, Always, Never: An odd number has an odd amount of factors True or False? The bigger the number, the more factors it has.. 18, 20, 24, 30, 36, 40. Sometimes e.g. 6 has four factors but 36 has 9 Sometimes. E.g. 21 has 4 factors but 25 has an odd number (3), This is false e.g. 12 has 6 factors but 97 only has 2.
6 Year 5 Autumn Term Teaching Guidance Common Factors Notes and Guidance Using their knowledge of factors, children find the common factors of two numbers. They use arrays to compare the factors of a number and use a Venn diagram to show their results. 1 Use arrays to find the common factors of 12 and 15 Can we arrange the counters in one row? Yes- so they have a common factor of one. Can we arrange the counters in two equal rows? Mathematical Talk How can we find the common factors systematically? Which number is a common factor of any pair of numbers? How does a Venn diagram help to find common factors? Where are the common factors? 2 2 is a factor of 12 but not of 15 so 2 is not a common factor. Continue to work through the factors systematically until you find all the common factors. Fill in the Venn diagram to find the factors of 20 and 24. Where are the common factors of 20 and 24? Can you use a Venn diagram to find the common factors of 9 and 15?
7 Year 5 Autumn Term Common Factors Reasoning and Problem Solving True or False? 1 is a factor of every number. 1 is a multiple of every number 0 is a factor if every number 0 is a multiple of every number True 1 is a factor of every number False 1 is only a multiple of 1 False 0 is only a factor of 0 I am thinking of two 2-digit numbers. Both of the numbers have a digit total of 6 Their common factors are 1, 2, 3, 4, 6, & 12 What are the numbers? The numbers are 24 & 60. True 0 multiplied by any number equals 0..
8 Year 5 Autumn Term Teaching Guidance Prime Numbers Notes and Guidance Using their knowledge of factors, children see that some numbers only have 2 factors and these are special numbers called Prime Numbers. They also learn that non-primes are called composite numbers. Children can recall primes up to 19 and are able to establish whether a number is prime up to 100. Using primes, they break a number down into its prime factors. Mathematical Talk How many factors does each number have? How many other numbers can you find that have this number of factors? What is a prime number? What is a composite number? How many factors does a prime number have? 2 1 Use counters to find the factors of the following numbers. 5, 13, 17, 23 What do you notice about the arrays? A prime number has 2 factors, one and itself. A composite number can be divided by numbers other than 1 and itself. Sort the numbers into the table factors (1 & itself) More than 2 factors Prime Composite Put two of your own numbers into the table. Why are two of the boxes empty? Where would 1 go in the table? Would it fit in at all?
9 Year 5 Autumn Term Prime Numbers Reasoning and Problem Solving Find all the prime number between 10 and 100, Sort them in the table below. End in a 1 End in a 3 End in a 7 End in a 9 What is the same about the groups? Why do no two-digit prime numbers end in an even number? Why do no two-digit prime numbers end in a 5? End in a 1 End in a 3 11, 31, 41, 61, 71, 13, 23, 43, 53, 73, 83 End in a 7 End in a 9 17, 37, 47, 67, 97 19, 29, 59, 79, 89 No 2-digit primes end in an even number because 2- digit even numbers are divisible by 2. No 2- digit prime numbers end in a 5 because they are divisible by 5 as well as 1 and itself. Katie says all prime numbers have to be odd. Her friend Abdul That means 9, 27 and 45 are prime numbers. Explain Abdul and Katie s mistakes and correct them. Always, sometimes, never The sum of two prime numbers is even. 2 is a prime number so Katie is wrong. Abdul thinks all odd numbers are prime but he is wrong as the numbers he has chosen have more than 2 factors. 9= 1, 3 & 9 as factors 27 = 1, 3, 9 & = 1, 3, 5, 9, 15 & 45 Sometimes: The sum of any 2 odd prime numbers is even. However if you add 2 and another prime number your answer is odd.
10 Year 5 Autumn Term Teaching Guidance Square Numbers Notes and Guidance Children will need to be able to find factors of whole numbers. Square numbers have an odd number of factors and are the result of multiplying a number by itself. 1 What does this array show you?. Why is it square? They learn the notation for squared is 2. Mathematical Talk Why are square numbers called square numbers? Is there a pattern between the numbers? True or False: The square of an even number is even and the square of an odd number is odd 2 3 How many ways are there of arranging 36 counters? Explain what you notice about the different arrays. How many different squares can you make using counters? What do you notice? Are there any patterns? Find the first 12 square numbers. Prove that they are square numbers.
11 Year 5 Autumn Term Square Numbers Reasoning and Problem Solving Chris says Do you agree? Explain your reasoning. Factors come in pairs so all whole numbers must have an even number of factors. Children will find that some numbers don t have an even number of factors e.g. 25. Square numbers have an odd number of factors. Julian thinks that 4 2 is equal to 16. Do you agree? Convince me. He also thinks that 6 2 is equal to 12. Do you agree? Explain what you have noticed. Children may use concrete materials or draw pictures of to prove it. Children should spot that 6 has been multiplied by 2. How many square numbers can you make by adding prime numbers together? Here s one to get you started: = 4. Solutions include: = = = = = 36 Always, Sometimes, Never: A square number has an even number of factors. They may create the array to prove that 6 2 = 36 and 6 2 = 12 Never. Square numbers have an odd number of factors.
12 Year 5 Autumn Term Teaching Guidance Cube Numbers Notes and Guidance Children learn that a cubed number is the product of three numbers which are the same. If you multiply a number by itself, then itself again the result is a cubed number. They learn the notation for cubed is 3 Mathematical Talk How are squared and cubed numbers the same? How are they different? True or False: Cubes of even numbers are even and cubes of odd numbers are odd 1 Use multilink cubes and investigate how many are needed to make different sized cubes. How many multilink cubes are required to make the first cubed number? The second? Third? Can you predict what the tenth cubed number is going to be? 2 Complete the following table. 3 Calculate: = 5 3 = 4 cubed= 6 cubed=
13 Year 5 Autumn Term Cube Numbers Reasoning and Problem Solving Lisa says. 5 3 is equal to 15 No- She has multiplied 5 times three rather than 5 times 5 times 5 Jenny is thinking of a two-digit number that is both a square and a cubed number. What number is she thinking of? 64 Is she correct? Caroline s daughter has an age that is a cubed number. 8 Here are 3 number cards A B C A = 8 B = 64 C = 125 Next year her age will be a squared number. How old is she now? Each number card is a cubed number. Use the following information to find each number A A = B The sum of a cubed number and a square number is 150. What are the two numbers? 125 & 25 B + B 3 = C Digit total of C = A
14 Year 5 Autumn Term Teaching Guidance Multiplying by 10, 100 & 1000 Notes and Guidance Children recap multiplying by 10 and 100 before moving on to multiplying by They look at numbers in a place value grid and discuss how many places to the left digits move when you multiply by different multiples of Make the number 234 on the place value grid using counters. HTh TTh Th H T O Mathematical Talk Which direction do the digits move when you multiply by 10, 100 or 1000? How many places do you move to the left? When we have an empty place value column to the right of our digits what number do we use as a place holder? Can you use multiplying by 100 to help you multiply by 1000? Explain why. 2 3 When I multiply my number by 10, where will I move my counters? Remember when we multiply by 10, 100, 1000, we move the digits to the left and use zero as a place holder. Complete the following questions using counters and a place value grid = = = 1, = 45, = = 3,456 1,000 Use <,> or = to complete the sentences. 62 1,
15 Year 5 Autumn Term Multiplying by 10, 100 & 1000 Reasoning and Problem Solving Rosie has 300 in her bank account. Louis has 100 times more than Rosie in his bank account. How much more money does Louis have than Rosie? Rosie has 300 Louis has 30,000 Louis has 27,700 more than Rosie. Jack is thinking of a 3-digit number. When he multiplies his number by 100, the ten thousands and hundreds digit are the same. The sum of the digits is , 262, 343, 424, 505 Emily has 1020 in her bank account and Philip has 120 in his bank account. Emily says, I have ten times more money than you. Is Emily correct? Explain your reasoning. No. Emily would have 1200 if this was the case. What number could Jack be thinking of?
16 Year 5 Autumn Term Teaching Guidance Dividing by 10, 100 & 1000 Notes and Guidance Children look at dividing by 10, 100 and 1000 using a place value chart. They use counters and digits to learn that the digits move to the right when dividing by powers of ten. 1 HTh TTh Th H T O Mathematical Talk What happens to the digits? How are dividing by 10, 100 and 1,000 related to each other? How are dividing by 10, 100 and 1,000 linked to multiplying by 10, 100 and 1,000? What does inverse mean? What number is represented in the place value grid? Divide the number by 100. Which direction do the counters move? How many columns do they move? What number do we have now? 2 Complete the following using the place value grid. Divide 460 by 10 Divide 5,300 by 100 Divide 62,000 by 1000 Divide the following numbers by 10, 100 and , , ,000 3 Calculate 45, How else could you write this?
17 Year 5 Autumn Term Dividing by 10, 100 & 1000 Reasoning and Problem Solving David has 357,000 in his bank. He divides the amount by 1,000 and takes that much money out of the bank. Using the money he has taken out he spends 269 on furniture for his new house. How much money does David have left from the money he took out? Show your workings out. Apples weigh about 160g each. How many apples would you expect to get in a 2kg bag? Explain your reasoning. 357,00 1,000 = 357 If you subtract 269, he is left with 88 Children need to be able to use knowledge of equivalent measures to convert 2kg to 2,000g. There are approximately 12 apples. Here are the answers to some problems: ,203 Can you write at least two questions for each answer involving dividing by 10, 100 or 1000? Match the calculation to the answer: 64, 640, 6,400 64, , , , , , How do you know? Do any of the calculations have the same answers? Is there an answer missed out? Explain what you have found. Possible solutions could be: = , = 5, , = , = , = 6,203 The missing answer is 64,000. Children could use place value grids to demonstrate the digits moving columns.
18 Year 5 Autumn Term Teaching Guidance Multiples of 10, 100 & 1000 Notes and Guidance Children have been taught how to multiply and divide by 10, 100 and They now use knowledge of other multiples to calculate related questions. Mathematical Talk If we are multiplying by 20, can we break it down into two steps and use our knowledge of multiplying by 10? How does using multiplication and division as inverses help us use known facts? = 180 Use this Varied fact to solve Fluency the following questions: = = = = 2 Here are two methods to solve Method = = 480 What is the same about the methods, what is different? 3 Use the division diagram to help solve the calculations. 7, = 36 7, Method = = = = 3, = 18, = 5,400 _ = 27 = 6,
19 Year 5 Autumn Term Multiples of 10, 100 & 1000 Reasoning and Problem Solving Tim has answered a question. Here is his working out. Tim is not correct as he has partitioned 25 incorrectly. 6 7 = =.. He could have divided by 5 twice. Jemma The answer is 60 because all of the numbers are 10 times bigger. The correct answer should be 24 Jemma is wrong because = 4200 Is he correct? Explain your answer. Do you agree with Jemma? Explain your answer. and 6 70 = 420 So the answer should be 6
Released October Year. Small Steps Guidance and Examples. Block 4: Multiplication & Division
 Released October 2017 Year 5 Small Steps Guidance and Examples Block 4: Multiplication & Division Multiply and divide numbers mentally drawing upon known facts. Multiples Factors Common factors Prime numbers
Released October 2017 Year 5 Small Steps Guidance and Examples Block 4: Multiplication & Division Multiply and divide numbers mentally drawing upon known facts. Multiples Factors Common factors Prime numbers
Updated October 2017
 Updated October 2017 Roman numerals to 100 Round to the nearest 10 Round to the nearest 100 Count in 1,000s 1,000s, 100s, 10s and 1s Partitioning Number line to 10,000 1,000 more or less Compare numbers
Updated October 2017 Roman numerals to 100 Round to the nearest 10 Round to the nearest 100 Count in 1,000s 1,000s, 100s, 10s and 1s Partitioning Number line to 10,000 1,000 more or less Compare numbers
Year 3. Term by Term Objectives. Year 3 Overview. Spring Autumn. Summer. Number: Place Value
 Year 3 Autumn Term by Term Objectives Year 3 Year 3 Overview Spring Autumn Number: Place Value Number: Multiplication and Division Number: Addition and Subtraction Number: Multiplication and Division Measurement
Year 3 Autumn Term by Term Objectives Year 3 Year 3 Overview Spring Autumn Number: Place Value Number: Multiplication and Division Number: Addition and Subtraction Number: Multiplication and Division Measurement
Count in multiples of 6, 7, and Find 1000 more or less than a given number.
 Roman numerals to 100 Round to the nearest 10 Round to the nearest 100 Count in 1,000s 1,000s, 100s, 10s and 1s Partitioning Number line to 10,000 1,000 more or less Compare numbers Order numbers Round
Roman numerals to 100 Round to the nearest 10 Round to the nearest 100 Count in 1,000s 1,000s, 100s, 10s and 1s Partitioning Number line to 10,000 1,000 more or less Compare numbers Order numbers Round
Addition 10=5+5. Vocabulary NB:H=hundreds/T=Tens/O=ones
 Addition Vocabulary NB:H=hundreds/T=Tens/O=ones number bonds, number line, add, more, plus, make, sum, total, altogether, double, how many more?, column addition, partition, counting on, efficient method,
Addition Vocabulary NB:H=hundreds/T=Tens/O=ones number bonds, number line, add, more, plus, make, sum, total, altogether, double, how many more?, column addition, partition, counting on, efficient method,
An ordered collection of counters in rows or columns, showing multiplication facts.
 Addend A number which is added to another number. Addition When a set of numbers are added together. E.g. 5 + 3 or 6 + 2 + 4 The answer is called the sum or the total and is shown by the equals sign (=)
Addend A number which is added to another number. Addition When a set of numbers are added together. E.g. 5 + 3 or 6 + 2 + 4 The answer is called the sum or the total and is shown by the equals sign (=)
Released November /2. Small Steps Guidance and Examples. Block 4: Measurement - Money
 Released November 2017 1/2 Small Steps Guidance and Examples Block 4: Measurement - Money Year 1/2 Autumn Term Teaching Guidance Overview Small Steps Year 1 Year 2 Recognising coins Recognising notes Counting
Released November 2017 1/2 Small Steps Guidance and Examples Block 4: Measurement - Money Year 1/2 Autumn Term Teaching Guidance Overview Small Steps Year 1 Year 2 Recognising coins Recognising notes Counting
Mental Calculation Policy 2014
 Mental Calculation Policy 2014 RECEPTION Children count reliably with numbers from one to 20 and place them in order. Children can say which number is one more or one less than a given number up to 20
Mental Calculation Policy 2014 RECEPTION Children count reliably with numbers from one to 20 and place them in order. Children can say which number is one more or one less than a given number up to 20
Children to write number sentences Children to show jumps on laminated number line: Show the jumps on a number line as counting on e.
 Written Methods& Mental Methods & A D D I T I O N FOUNDATION STAGE YEAR 1 YEAR 2 Count with 1:1 correspondence Recognise numbers Count to 20 and beyond Write numbers Order numbers to 20 Know one more than
Written Methods& Mental Methods & A D D I T I O N FOUNDATION STAGE YEAR 1 YEAR 2 Count with 1:1 correspondence Recognise numbers Count to 20 and beyond Write numbers Order numbers to 20 Know one more than
Meet the Characters 3. Yearly Overview 4. Block 1 Number: Multiplication and Division 5. Block 2 Measurement: Money 25. Block 3 Statistics 37
 1 Meet the Characters 3 Yearly Overview 4 Spring Blocks Block 1 Number: Multiplication and Division 5 Block 2 Measurement: Money 25 Block 3 Statistics 37 Block 4 Measurement: Length and Perimeter 45 Block
1 Meet the Characters 3 Yearly Overview 4 Spring Blocks Block 1 Number: Multiplication and Division 5 Block 2 Measurement: Money 25 Block 3 Statistics 37 Block 4 Measurement: Length and Perimeter 45 Block
Year 1 Spring Term Week 5 to 7 Number: Place Value (within 50)
 1 Numbers to 50 Tens and ones Represent numbers to 50 One more one less Compare objects within 50 Compare numbers within 50 Order numbers within 50 Count in 2s Count in 5s Count to 50 forwards and backwards,
1 Numbers to 50 Tens and ones Represent numbers to 50 One more one less Compare objects within 50 Compare numbers within 50 Order numbers within 50 Count in 2s Count in 5s Count to 50 forwards and backwards,
Year 1. Place Value. Term by Term Objectives. All students Fluency Reasoning Problem Solving. National Curriculum Statement
 National Curriculum Place Value Given a number, identify one more or one less. 9 2 Fill in the missing numbers. Is 1 less than Is 1 more than How many fingers if I put one down? I roll the number that
National Curriculum Place Value Given a number, identify one more or one less. 9 2 Fill in the missing numbers. Is 1 less than Is 1 more than How many fingers if I put one down? I roll the number that
Released January Years 3/4. Small Steps Guidance and Examples. Block 2 Length, Perimeter, Area
 Released January 208 Years 3/4 Small Steps Guidance and Examples Block 2 Length, Perimeter, Area Year 3/4 Spring Term Teaching Guidance Overview Small Steps Year 3 Year 4 Measure length Equivalent lengths
Released January 208 Years 3/4 Small Steps Guidance and Examples Block 2 Length, Perimeter, Area Year 3/4 Spring Term Teaching Guidance Overview Small Steps Year 3 Year 4 Measure length Equivalent lengths
4 + 3 = 7 10= model. Starting at the bigger number and counting on
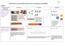 South Wilford C of E Endowed Primary School - Progression in Calculations Addition Objective and Strategies Combining two parts to make a whole: partpart whole model Concrete Pictorial Abstract Use cubes
South Wilford C of E Endowed Primary School - Progression in Calculations Addition Objective and Strategies Combining two parts to make a whole: partpart whole model Concrete Pictorial Abstract Use cubes
This policy has been largely adapted from the White Rose Maths Hub Calculation Policy with further material added.
 This policy has been largely adapted from the White Rose Maths Hub Calculation Policy with further material added. St John s RC Primary School Calculation Combining two parts to make a whole: part- whole
This policy has been largely adapted from the White Rose Maths Hub Calculation Policy with further material added. St John s RC Primary School Calculation Combining two parts to make a whole: part- whole
Progression In Calculations Addition
 Objective and Strategies Combining two parts to make a whole: partwhole model Addition Concrete Pictorial Abstract Use cubes to add two numbers together as a group or in a bar. Use pictures to add two
Objective and Strategies Combining two parts to make a whole: partwhole model Addition Concrete Pictorial Abstract Use cubes to add two numbers together as a group or in a bar. Use pictures to add two
4 + 3 = 7 10= Starting at the bigger number and counting on. Progression in Calculations
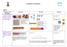 Progression in Calculations Addition Objective and Strategies Combining two parts to make a whole: partwhole model Concrete Pictorial Abstract Use cubes to add two numbers together as a group or in a bar.
Progression in Calculations Addition Objective and Strategies Combining two parts to make a whole: partwhole model Concrete Pictorial Abstract Use cubes to add two numbers together as a group or in a bar.
1. Copy and complete each number pattern. a b c. 51 kg 51,2kg 51,8kg d
 125 Unit 2. Whole Numbers: Addition and Subtraction (6 digit numbers). Activity 1. Whole Numbers. 1. Copy and complete each number pattern. a. 21 200 19 200 11 200 b. 4 625 5 000 5 500 c. 51 kg 51,2kg
125 Unit 2. Whole Numbers: Addition and Subtraction (6 digit numbers). Activity 1. Whole Numbers. 1. Copy and complete each number pattern. a. 21 200 19 200 11 200 b. 4 625 5 000 5 500 c. 51 kg 51,2kg
An Overview of Mathematics 4
 An Overview of Mathematics 4 Number (N) read, write, represent, and describe whole numbers to 10 000 using concrete materials, pictures, expressions (e.g., 400 + 7), words, place-value charts, and symbols
An Overview of Mathematics 4 Number (N) read, write, represent, and describe whole numbers to 10 000 using concrete materials, pictures, expressions (e.g., 400 + 7), words, place-value charts, and symbols
Whole Numbers WHOLE NUMBERS PASSPORT.
 WHOLE NUMBERS PASSPORT www.mathletics.co.uk It is important to be able to identify the different types of whole numbers and recognise their properties so that we can apply the correct strategies needed
WHOLE NUMBERS PASSPORT www.mathletics.co.uk It is important to be able to identify the different types of whole numbers and recognise their properties so that we can apply the correct strategies needed
Updated October 2017
 Updated October 2017 Count objects to 100 and read and write numbers in numerals and words Represent numbers to 100 Tens and ones with a part whole model Tens and ones using addition Use a place alue chart
Updated October 2017 Count objects to 100 and read and write numbers in numerals and words Represent numbers to 100 Tens and ones with a part whole model Tens and ones using addition Use a place alue chart
GRADE 3 TEKS ALIGNMENT CHART
 GRADE 3 TEKS ALIGNMENT CHART TEKS 3.2.A compose and decompose numbers up to,000 as the sum of so many ten thousands, so many thousands, so many hundreds, so many tens, and so many ones using objects, pictorial
GRADE 3 TEKS ALIGNMENT CHART TEKS 3.2.A compose and decompose numbers up to,000 as the sum of so many ten thousands, so many thousands, so many hundreds, so many tens, and so many ones using objects, pictorial
4 + 3 = 7 10= Starting at the bigger number and counting on
 Ladbrooke JMI School Progression in Calculations Addition Objective and Strategies Combining two parts to make a whole: partwhole model Concrete Pictorial Abstract Use cubes to add two numbers together
Ladbrooke JMI School Progression in Calculations Addition Objective and Strategies Combining two parts to make a whole: partwhole model Concrete Pictorial Abstract Use cubes to add two numbers together
Numeracy Warm Up. Introduction
 Numeracy Warm Up Introduction Numeracy Warm Up is a set of numeracy exercises that can be used for starters, main lessons and plenaries. It is aimed at Numeracy lessons covering National Curriculum Levels
Numeracy Warm Up Introduction Numeracy Warm Up is a set of numeracy exercises that can be used for starters, main lessons and plenaries. It is aimed at Numeracy lessons covering National Curriculum Levels
Study Guide: 5.3 Prime/Composite and Even/Odd
 Standard: 5.1- The student will a) identify and describe the characteristics of prime and composite numbers; and b) identify and describe the characteristics of even and odd numbers. What you need to know
Standard: 5.1- The student will a) identify and describe the characteristics of prime and composite numbers; and b) identify and describe the characteristics of even and odd numbers. What you need to know
4 + 3 = 7 10= Combining two parts to make a whole: partwhole. Starting at the bigger number and counting on
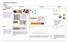 Progression in Calculations Addition Objective and Strategies R/Y1 Combining two parts to make a whole: partwhole model Concrete Pictorial Abstract Use cubes to add two numbers together as a group or in
Progression in Calculations Addition Objective and Strategies R/Y1 Combining two parts to make a whole: partwhole model Concrete Pictorial Abstract Use cubes to add two numbers together as a group or in
Sample pages. Multiples, factors and divisibility. Recall 2. Student Book
 52 Recall 2 Prepare for this chapter by attempting the following questions. If you have difficulty with a question, go to Pearson Places and download the Recall from Pearson Reader. Copy and complete these
52 Recall 2 Prepare for this chapter by attempting the following questions. If you have difficulty with a question, go to Pearson Places and download the Recall from Pearson Reader. Copy and complete these
Is muddled about the correspondence between multiplication and division facts, recording, for example: 3 5 = 15, so 5 15 = 3
 Is muddled about the correspondence between multiplication and division facts, recording, for example: 3 5 = 15, so 5 15 = 3 Opportunity for: recognising relationships Resources Board with space for four
Is muddled about the correspondence between multiplication and division facts, recording, for example: 3 5 = 15, so 5 15 = 3 Opportunity for: recognising relationships Resources Board with space for four
Year 1. Mastery Overview Autumn
 Mastery Overview Autumn SOL Overview As well as providing term by term overviews for the new as a Maths Hub we are aiming to support primary schools by providing more detailed Schemes of Learning, which
Mastery Overview Autumn SOL Overview As well as providing term by term overviews for the new as a Maths Hub we are aiming to support primary schools by providing more detailed Schemes of Learning, which
The Willows Primary School Mental Mathematics Policy
 The Willows Primary School Mental Mathematics Policy The Willows Primary Mental Maths Policy Teaching methodology and organisation Teaching time All pupils will receive between 10 and 15 minutes of mental
The Willows Primary School Mental Mathematics Policy The Willows Primary Mental Maths Policy Teaching methodology and organisation Teaching time All pupils will receive between 10 and 15 minutes of mental
There are 5 people upstairs on the bus, there are 4 people downstairs. How many altogether? Write a number sentence to show this.
 National Curriculum Fluency Reasoning Problem Solving Read, write and interpret mathematical statements involving addition (+), subtraction (-) and equals (=) signs. There are 5 people upstairs on the
National Curriculum Fluency Reasoning Problem Solving Read, write and interpret mathematical statements involving addition (+), subtraction (-) and equals (=) signs. There are 5 people upstairs on the
Whole Numbers. Whole Numbers. Curriculum Ready.
 Curriculum Ready www.mathletics.com It is important to be able to identify the different types of whole numbers and recognize their properties so that we can apply the correct strategies needed when completing
Curriculum Ready www.mathletics.com It is important to be able to identify the different types of whole numbers and recognize their properties so that we can apply the correct strategies needed when completing
Use each digit card once to make the decimal number nearest to 20
 NUMBER Level 4 questions 1. Here is a number chart. Circle the smallest number on the chart that is a multiple of both 2 and 7 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
NUMBER Level 4 questions 1. Here is a number chart. Circle the smallest number on the chart that is a multiple of both 2 and 7 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95
GPLMS Revision Programme GRADE 6 Booklet
 GPLMS Revision Programme GRADE 6 Booklet Learner s name: School name: Day 1. 1. a) Study: 6 units 6 tens 6 hundreds 6 thousands 6 ten-thousands 6 hundredthousands HTh T Th Th H T U 6 6 0 6 0 0 6 0 0 0
GPLMS Revision Programme GRADE 6 Booklet Learner s name: School name: Day 1. 1. a) Study: 6 units 6 tens 6 hundreds 6 thousands 6 ten-thousands 6 hundredthousands HTh T Th Th H T U 6 6 0 6 0 0 6 0 0 0
High-Impact Games and Meaningful Mathematical Dialog Grades 3-5
 NCTM 2017 San Antonio, Texas High-Impact Games and Meaningful Mathematical Dialog Grades 3-5 Elizabeth Cape Jennifer Leimberer Sandra Niemiera mathtrailblazers@uic.edu Teaching Integrated Math and Science
NCTM 2017 San Antonio, Texas High-Impact Games and Meaningful Mathematical Dialog Grades 3-5 Elizabeth Cape Jennifer Leimberer Sandra Niemiera mathtrailblazers@uic.edu Teaching Integrated Math and Science
Second Quarter Benchmark Expectations for Units 3 and 4
 Mastery Expectations For the Second Grade Curriculum In Second Grade, Everyday Mathematics focuses on procedures, concepts, and s in four critical areas: Understanding of base-10 notation. Building fluency
Mastery Expectations For the Second Grade Curriculum In Second Grade, Everyday Mathematics focuses on procedures, concepts, and s in four critical areas: Understanding of base-10 notation. Building fluency
NUMBER, NUMBER SYSTEMS, AND NUMBER RELATIONSHIPS. Kindergarten:
 Kindergarten: NUMBER, NUMBER SYSTEMS, AND NUMBER RELATIONSHIPS Count by 1 s and 10 s to 100. Count on from a given number (other than 1) within the known sequence to 100. Count up to 20 objects with 1-1
Kindergarten: NUMBER, NUMBER SYSTEMS, AND NUMBER RELATIONSHIPS Count by 1 s and 10 s to 100. Count on from a given number (other than 1) within the known sequence to 100. Count up to 20 objects with 1-1
Foundations of Multiplication and Division
 Grade 2 Module 6 Foundations of Multiplication and Division OVERVIEW Grade 2 Module 6 lays the conceptual foundation for multiplication and division in Grade 3 and for the idea that numbers other than
Grade 2 Module 6 Foundations of Multiplication and Division OVERVIEW Grade 2 Module 6 lays the conceptual foundation for multiplication and division in Grade 3 and for the idea that numbers other than
GRADE 4. M : Solve division problems without remainders. M : Recall basic addition, subtraction, and multiplication facts.
 GRADE 4 Students will: Operations and Algebraic Thinking Use the four operations with whole numbers to solve problems. 1. Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 7 as
GRADE 4 Students will: Operations and Algebraic Thinking Use the four operations with whole numbers to solve problems. 1. Interpret a multiplication equation as a comparison, e.g., interpret 35 = 5 7 as
MATH NUMBER SENSE 3 Performance Objective Task Analysis Benchmarks/Assessment Students: 1. Students understand place value of whole numbers.
 Students: 1. Students understand place value of whole numbers. 1. Count, read, and write whole numbers to 10,000. Count to 10,000 Which numbers are whole numbers? Whole number 0, 15.3, 4/5, 8, 25 1/2 Count
Students: 1. Students understand place value of whole numbers. 1. Count, read, and write whole numbers to 10,000. Count to 10,000 Which numbers are whole numbers? Whole number 0, 15.3, 4/5, 8, 25 1/2 Count
Hundreds Grid. MathShop: Hundreds Grid
 Hundreds Grid MathShop: Hundreds Grid Kindergarten Suggested Activities: Kindergarten Representing Children create representations of mathematical ideas (e.g., use concrete materials; physical actions,
Hundreds Grid MathShop: Hundreds Grid Kindergarten Suggested Activities: Kindergarten Representing Children create representations of mathematical ideas (e.g., use concrete materials; physical actions,
GPLMS Revision Programme GRADE 4 Booklet
 GPLMS Revision Programme GRADE 4 Booklet Learner s name: School name: Day 1. 1. Read carefully: a) The place or position of a digit in a number gives the value of that digit. b) In the number 4237, 4,
GPLMS Revision Programme GRADE 4 Booklet Learner s name: School name: Day 1. 1. Read carefully: a) The place or position of a digit in a number gives the value of that digit. b) In the number 4237, 4,
Georgia Department of Education Common Core Georgia Performance Standards Framework Fifth Grade Mathematics Unit 2
 PRACTICE TASK: Adapted from Investigations in Number, Data, and Space: How Many Tens? How Many Ones? Addition, Subtraction, and the Number System. STANDARDS FOR MATHEMATICAL CONTENT MCC5.NBT.7 Add, subtract,
PRACTICE TASK: Adapted from Investigations in Number, Data, and Space: How Many Tens? How Many Ones? Addition, Subtraction, and the Number System. STANDARDS FOR MATHEMATICAL CONTENT MCC5.NBT.7 Add, subtract,
3. If you can t make the sum with your cards, you must draw one card. 4. Players take turns rolling and discarding cards.
 1 to 10 Purpose: The object of the game is to get rid of all your cards. One player gets all the red cards, the other gets all the black cards. Players: 2-4 players Materials: 2 dice, a deck of cards,
1 to 10 Purpose: The object of the game is to get rid of all your cards. One player gets all the red cards, the other gets all the black cards. Players: 2-4 players Materials: 2 dice, a deck of cards,
National Curriculum Programme of Study:
 National Curriculum Programme of Study: Count to and across 100, forwards and backwards, beginning with 0 or 1, or from any given number Given a number, identify one more and one less Add and subtract
National Curriculum Programme of Study: Count to and across 100, forwards and backwards, beginning with 0 or 1, or from any given number Given a number, identify one more and one less Add and subtract
Grade 2 Arkansas Mathematics Standards. Represent and solve problems involving addition and subtraction
 Grade 2 Arkansas Mathematics Standards Operations and Algebraic Thinking Represent and solve problems involving addition and subtraction AR.Math.Content.2.OA.A.1 Use addition and subtraction within 100
Grade 2 Arkansas Mathematics Standards Operations and Algebraic Thinking Represent and solve problems involving addition and subtraction AR.Math.Content.2.OA.A.1 Use addition and subtraction within 100
The Eliot Bank and Gordonbrock Schools Federation. Calculation Policy. Addition Subtraction Multiplication Division Take away practically
 Reception Counting to make total practically Take away practically Drawing objects Drawing objects and crossing out Tallying/mark making Using a completed number track to count on. Using a completed number
Reception Counting to make total practically Take away practically Drawing objects Drawing objects and crossing out Tallying/mark making Using a completed number track to count on. Using a completed number
S P R I N G B O A R D 5 S P R I N G B O A R D UNIT SUPPLEMENTARY TEACHING SEQUENCES
 TEACHING SEQUENCES Springboard supplementary Unit SEQUENCE 1 Multiplication sequence RESOURCES: ITP Multiplication Facts (on the accompanying CD-ROM in ITPs Index) or board where arrays can be constructed
TEACHING SEQUENCES Springboard supplementary Unit SEQUENCE 1 Multiplication sequence RESOURCES: ITP Multiplication Facts (on the accompanying CD-ROM in ITPs Index) or board where arrays can be constructed
Counters in a Cup In and Out. The student sets up the cup, drops the counters on it, and records how many landed in and out of the cup.
 Counters in a Cup In and Out Cup Counters Recording Paper The student sets up the cup, drops the counters on it, and records how many landed in and out of the cup. 3 + 4 =7 2 + 5 =7 For subtraction, take
Counters in a Cup In and Out Cup Counters Recording Paper The student sets up the cup, drops the counters on it, and records how many landed in and out of the cup. 3 + 4 =7 2 + 5 =7 For subtraction, take
GRADE 4 MATHS SYLLABUS - FIRST TERM SYLLABUS INSTAMATHS WKSHEET 1-14
 GRADE 4 MATHS SYLLABUS - FIRST TERM INSTAMATHS EXERCISES 1; 2; 3; 4; 4; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 50; 51; 54; 55; 56; 57; 58; 60; 61; 73; 90;; 92 SYLLABUS INSTAMATHS WKSHEET 1-14 TEXT
GRADE 4 MATHS SYLLABUS - FIRST TERM INSTAMATHS EXERCISES 1; 2; 3; 4; 4; 6; 7; 8; 9; 10; 11; 12; 13; 14; 15; 16; 17; 50; 51; 54; 55; 56; 57; 58; 60; 61; 73; 90;; 92 SYLLABUS INSTAMATHS WKSHEET 1-14 TEXT
Multiplication and Division
 E Student Book 6 7 = 4 Name Series E Contents Topic Multiplication facts (pp. 7) 5 and 0 times tables and 4 times tables 8 times table and 6 times tables Date completed Topic Using known facts (pp. 8 )
E Student Book 6 7 = 4 Name Series E Contents Topic Multiplication facts (pp. 7) 5 and 0 times tables and 4 times tables 8 times table and 6 times tables Date completed Topic Using known facts (pp. 8 )
MAKING MATHEMATICS COUNT
 MAKING MATHEMATICS COUNT By Kerry Dalton Using manipulatives from Early Years Foundation Stage to Year 6 10 minutes per day, in addition to the daily mathematics lesson Covers Early Years Foundation Stage
MAKING MATHEMATICS COUNT By Kerry Dalton Using manipulatives from Early Years Foundation Stage to Year 6 10 minutes per day, in addition to the daily mathematics lesson Covers Early Years Foundation Stage
Focus on Mathematics
 Focus on Mathematics Year 4 Pre-Learning Tasks Number Pre-learning tasks are used at the start of each new topic in Maths. The children are grouped after the pre-learning task is marked to ensure the work
Focus on Mathematics Year 4 Pre-Learning Tasks Number Pre-learning tasks are used at the start of each new topic in Maths. The children are grouped after the pre-learning task is marked to ensure the work
Describes the operation of multiplying by ten as adding a nought
 Describes the operation of multiplying by ten as adding a nought Opportunity for: investigating numbers Interactive Teaching Program (ITP) Number Grid, how many times group or paper copy of 100-square
Describes the operation of multiplying by ten as adding a nought Opportunity for: investigating numbers Interactive Teaching Program (ITP) Number Grid, how many times group or paper copy of 100-square
Math Grade 2. Understand that three non-zero digits of a 3-digit number represent amounts of hundreds, tens and ones.
 Number Sense Place value Counting Skip counting Other names for numbers Comparing numbers Using properties or place value to add and subtract Standards to be addressed in Number Sense Standard Topic Term
Number Sense Place value Counting Skip counting Other names for numbers Comparing numbers Using properties or place value to add and subtract Standards to be addressed in Number Sense Standard Topic Term
Answers Solving mathematical problems
 Solving mathematical problems 1 in the middle (p.8) Many answers are possible, for example: 10, 11, 1, 13, 14 (on in steps of 1) 14, 13, 1, 11, 10 (back in steps of 1) 8, 10, 1, 14, 16 (on in steps of
Solving mathematical problems 1 in the middle (p.8) Many answers are possible, for example: 10, 11, 1, 13, 14 (on in steps of 1) 14, 13, 1, 11, 10 (back in steps of 1) 8, 10, 1, 14, 16 (on in steps of
NAME DATE. b) Then do the same for Jett s pennies (6 sets of 9 pennies with 4 leftover pennies).
 NAME DATE 1.2.2/1.2.3 NOTES 1-51. Cody and Jett each have a handful of pennies. Cody has arranged his pennies into 3 sets of 16, and has 9 leftover pennies. Jett has 6 sets of 9 pennies, and 4 leftover
NAME DATE 1.2.2/1.2.3 NOTES 1-51. Cody and Jett each have a handful of pennies. Cody has arranged his pennies into 3 sets of 16, and has 9 leftover pennies. Jett has 6 sets of 9 pennies, and 4 leftover
Second Grade Mathematics Goals
 Second Grade Mathematics Goals Operations & Algebraic Thinking 2.OA.1 within 100 to solve one- and twostep word problems involving situations of adding to, taking from, putting together, taking apart,
Second Grade Mathematics Goals Operations & Algebraic Thinking 2.OA.1 within 100 to solve one- and twostep word problems involving situations of adding to, taking from, putting together, taking apart,
Operation Target. Round Number Sentence Target How Close? Building Fluency: creating equations and the use of parentheses.
 Operations and Algebraic Thinking 5. OA.1 2 Operation Target Building Fluency: creating equations and the use of parentheses. Materials: digit cards (0-9) and a recording sheet per player Number of Players:
Operations and Algebraic Thinking 5. OA.1 2 Operation Target Building Fluency: creating equations and the use of parentheses. Materials: digit cards (0-9) and a recording sheet per player Number of Players:
Roll & Make. Represent It a Different Way. Show Your Number as a Number Bond. Show Your Number on a Number Line. Show Your Number as a Strip Diagram
 Roll & Make My In Picture Form In Word Form In Expanded Form With Money Represent It a Different Way Make a Comparison Statement with a Greater than Your Make a Comparison Statement with a Less than Your
Roll & Make My In Picture Form In Word Form In Expanded Form With Money Represent It a Different Way Make a Comparison Statement with a Greater than Your Make a Comparison Statement with a Less than Your
9. [Decimals] Tenths: There are 6 rows completely shaded 6 tenths Hundredths: There are 4 shaded squares in the shorter row. 4 hundredths = 0.
![9. [Decimals] Tenths: There are 6 rows completely shaded 6 tenths Hundredths: There are 4 shaded squares in the shorter row. 4 hundredths = 0. 9. [Decimals] Tenths: There are 6 rows completely shaded 6 tenths Hundredths: There are 4 shaded squares in the shorter row. 4 hundredths = 0.](/thumbs/89/98726801.jpg) 9. [Decimals] Skill 9.1 Counting tenths and hundredths in a 10 10 grid (1). Count the number of squares in 1 row or 1 column. Hint: Each row (or column) shows 10 tenths. The whole grid shows 100 hundredths.
9. [Decimals] Skill 9.1 Counting tenths and hundredths in a 10 10 grid (1). Count the number of squares in 1 row or 1 column. Hint: Each row (or column) shows 10 tenths. The whole grid shows 100 hundredths.
Released October Year. Small Steps Guidance and Examples. Block 5: Perimeter and Area
 Released October 2017 Year 5 Small Steps Guidance and Examples Block 5: Perimeter and Area Measure perimeter Calculate perimeter Find unknown lengths Area of rectangles Area of compound shapes Estimate
Released October 2017 Year 5 Small Steps Guidance and Examples Block 5: Perimeter and Area Measure perimeter Calculate perimeter Find unknown lengths Area of rectangles Area of compound shapes Estimate
Mathematics Grade 2. grade 2 17
 Mathematics Grade 2 In Grade 2, instructional time should focus on four critical areas: (1) extending understanding of base-ten notation; (2) building fluency with addition and subtraction; (3) using standard
Mathematics Grade 2 In Grade 2, instructional time should focus on four critical areas: (1) extending understanding of base-ten notation; (2) building fluency with addition and subtraction; (3) using standard
Saxon Math Manipulatives in Motion Primary. Correlations
 Saxon Math Manipulatives in Motion Primary Correlations Saxon Math Program Page Math K 2 Math 1 8 Math 2 14 California Math K 21 California Math 1 27 California Math 2 33 1 Saxon Math Manipulatives in
Saxon Math Manipulatives in Motion Primary Correlations Saxon Math Program Page Math K 2 Math 1 8 Math 2 14 California Math K 21 California Math 1 27 California Math 2 33 1 Saxon Math Manipulatives in
Example: I predict odd, roll a 5, and then collect that many counters. Play until time is up. The player with the most counters wins.
 Odds and Evens Skill: Identifying even and odd numbers Materials: 1 die to share 1. Each player takes 5 counters and puts the rest in a pile between them. 2. Player 1 predicts whether he will roll ODD
Odds and Evens Skill: Identifying even and odd numbers Materials: 1 die to share 1. Each player takes 5 counters and puts the rest in a pile between them. 2. Player 1 predicts whether he will roll ODD
Read, write, order and compare numbers to at least and determine the value of each digit.
 Number to 10,000 Roman numerals to 1,000 Round to the nearest 10, 100 and 1,000 Number to 100,000 Compare and order numbers to 100,000 Round numbers within 100,000 Numbers to a million Counting in 10s,
Number to 10,000 Roman numerals to 1,000 Round to the nearest 10, 100 and 1,000 Number to 100,000 Compare and order numbers to 100,000 Round numbers within 100,000 Numbers to a million Counting in 10s,
Chapter 2: Numeration Systems
 Chapter 2: Numeration Systems 8. In base ten, 215.687 is exactly ones, exactly tens, exactly hundreds, and exactly thousands; also, 3421 is exactly tenths and exactly hundredths. In base ten, 215.687 is
Chapter 2: Numeration Systems 8. In base ten, 215.687 is exactly ones, exactly tens, exactly hundreds, and exactly thousands; also, 3421 is exactly tenths and exactly hundredths. In base ten, 215.687 is
Review. Natural Numbers: Whole Numbers: Integers: Rational Numbers: Outline Sec Comparing Rational Numbers
 FOUNDATIONS Outline Sec. 3-1 Gallo Name: Date: Review Natural Numbers: Whole Numbers: Integers: Rational Numbers: Comparing Rational Numbers Fractions: A way of representing a division of a whole into
FOUNDATIONS Outline Sec. 3-1 Gallo Name: Date: Review Natural Numbers: Whole Numbers: Integers: Rational Numbers: Comparing Rational Numbers Fractions: A way of representing a division of a whole into
Contents. PART 1 Unit 1: Number Sense: Numbers to 10. Unit 2: Number Sense: Numbers to 20. Unit 3: Patterns and Algebra: Repeating Patterns
 Contents PART 1 Unit 1: Number Sense: Numbers to 10 NS2-1 Counting and Matching 1 NS2-2 One-to-One Correspondence 3 NS2-3 More, Fewer, and Less 5 NS2-4 How Many More? 7 NS2-5 Reading Number Words to Ten
Contents PART 1 Unit 1: Number Sense: Numbers to 10 NS2-1 Counting and Matching 1 NS2-2 One-to-One Correspondence 3 NS2-3 More, Fewer, and Less 5 NS2-4 How Many More? 7 NS2-5 Reading Number Words to Ten
Year 6 Spring Term Week 10 to 11 Number: Ratio
 1 Using ratio language Ratio and fractions Introducing the ratio symbol Calculating ratio Using scale factors Calculating scale factors Ratio and proportion problems Solve problems involving the relative
1 Using ratio language Ratio and fractions Introducing the ratio symbol Calculating ratio Using scale factors Calculating scale factors Ratio and proportion problems Solve problems involving the relative
Read and write numbers to at least 100 in numerals and in words. Recognise the place value of each digit in a two digit number (tens, ones)
 Count objects to 100 and read and write numbers in numerals and words Represent numbers to 100 Tens and ones with a part whole model Tens and ones using addition Use a place alue chart Compare objects
Count objects to 100 and read and write numbers in numerals and words Represent numbers to 100 Tens and ones with a part whole model Tens and ones using addition Use a place alue chart Compare objects
Standards for Mathematical Practice
 Common Core State Standards Mathematics Student: Teacher: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively Standards for Mathematical Practice 3. Construct
Common Core State Standards Mathematics Student: Teacher: 1. Make sense of problems and persevere in solving them. 2. Reason abstractly and quantitatively Standards for Mathematical Practice 3. Construct
Number Sense and Decimal Unit Notes
 Number Sense and Decimal Unit Notes Table of Contents: Topic Page Place Value 2 Rounding Numbers 2 Face Value, Place Value, Total Value 3 Standard and Expanded Form 3 Factors 4 Prime and Composite Numbers
Number Sense and Decimal Unit Notes Table of Contents: Topic Page Place Value 2 Rounding Numbers 2 Face Value, Place Value, Total Value 3 Standard and Expanded Form 3 Factors 4 Prime and Composite Numbers
Numbers Up! 1 Volcanic Panic Math Content
 Numbers Up! 1 Volcanic Panic Math Content Numbers Up! 1 Volcanic Panic Math Content...1 Number Range 1-5...2 Number Range 1-10...2 Number Range 0-10...3 Number Range 0-10...3 Number Range 0-20...4 Number
Numbers Up! 1 Volcanic Panic Math Content Numbers Up! 1 Volcanic Panic Math Content...1 Number Range 1-5...2 Number Range 1-10...2 Number Range 0-10...3 Number Range 0-10...3 Number Range 0-20...4 Number
WORKING WITH NUMBERS GRADE 7
 WORKING WITH NUMBERS GRADE 7 NAME: CLASS 3 17 2 11 8 22 36 15 3 ( ) 3 2 Left to Right Left to Right + Left to Right Back 2 Basics Welcome back! Your brain has been on holiday for a whilelet s see if we
WORKING WITH NUMBERS GRADE 7 NAME: CLASS 3 17 2 11 8 22 36 15 3 ( ) 3 2 Left to Right Left to Right + Left to Right Back 2 Basics Welcome back! Your brain has been on holiday for a whilelet s see if we
Released November /5. Small Steps Guidance and Examples. Block 4: Length & Perimeter
 Released November 2017 4/5 Small Steps Guidance and Examples Block 4: Length & Perimeter Year 4/5 Autumn Term Teaching Guidance Overview Small Steps Year 4 Year 5 Kilometres Perimeter on a grid Perimeter
Released November 2017 4/5 Small Steps Guidance and Examples Block 4: Length & Perimeter Year 4/5 Autumn Term Teaching Guidance Overview Small Steps Year 4 Year 5 Kilometres Perimeter on a grid Perimeter
2.NBT.1 20) , 200, 300, 400, 500, 600, 700, 800, NBT.2
 Saxon Math 2 Class Description: Saxon mathematics is based on the principle of developing math skills incrementally and reviewing past skills daily. It also incorporates regular and cumulative assessments.
Saxon Math 2 Class Description: Saxon mathematics is based on the principle of developing math skills incrementally and reviewing past skills daily. It also incorporates regular and cumulative assessments.
MATHEMATICS UTAH CORE GUIDES GRADE 2
 MATHEMATICS UTAH CORE GUIDES GRADE 2 UTAH STATE BOARD OF EDUCATION 250 EAST 500 SOUTH P.O. BOX 144200 SALT LAKE CITY, UTAH 84114-4200 SYDNEE DICKSON, Ed.D., STATE SUPERINTENDENT OF PUBLIC INSTRUCTION Operations
MATHEMATICS UTAH CORE GUIDES GRADE 2 UTAH STATE BOARD OF EDUCATION 250 EAST 500 SOUTH P.O. BOX 144200 SALT LAKE CITY, UTAH 84114-4200 SYDNEE DICKSON, Ed.D., STATE SUPERINTENDENT OF PUBLIC INSTRUCTION Operations
Developing Conceptual Understanding of Number. Set D: Number Theory
 Developing Conceptual Understanding of Number Set D: Number Theory Carole Bilyk cbilyk@gov.mb.ca Wayne Watt wwatt@mts.net Vocabulary digit hundred s place whole numbers even Notes Number Theory 1 odd multiple
Developing Conceptual Understanding of Number Set D: Number Theory Carole Bilyk cbilyk@gov.mb.ca Wayne Watt wwatt@mts.net Vocabulary digit hundred s place whole numbers even Notes Number Theory 1 odd multiple
4. Subtracting an even number from another even number gives an odd number. 5. Subtracting an odd number from another odd number gives an even number
 Level A 1. What is 78 32? A) 48 B) 110 C) 46 D) 34 2. What is 57 19? A) 37 B) 38 C) 42 D) 32 3. What is 66 8? A) 58 B) 57 C) 52 D) 42 4. Subtracting an even number from another even number gives an odd
Level A 1. What is 78 32? A) 48 B) 110 C) 46 D) 34 2. What is 57 19? A) 37 B) 38 C) 42 D) 32 3. What is 66 8? A) 58 B) 57 C) 52 D) 42 4. Subtracting an even number from another even number gives an odd
Minute Simplify: 12( ) = 3. Circle all of the following equal to : % Cross out the three-dimensional shape.
 Minute 1 1. Simplify: 1( + 7 + 1) =. 7 = 10 10. Circle all of the following equal to : 0. 0% 5 100. 10 = 5 5. Cross out the three-dimensional shape. 6. Each side of the regular pentagon is 5 centimeters.
Minute 1 1. Simplify: 1( + 7 + 1) =. 7 = 10 10. Circle all of the following equal to : 0. 0% 5 100. 10 = 5 5. Cross out the three-dimensional shape. 6. Each side of the regular pentagon is 5 centimeters.
Montessori Rationale. study and materials. She brought us the phrase follow the child, as that is how we might all
 Montessori Rationale Melissa Plunkett Montessori has allowed for the development of a peaceful and whole child with her study and materials. She brought us the phrase follow the child, as that is how we
Montessori Rationale Melissa Plunkett Montessori has allowed for the development of a peaceful and whole child with her study and materials. She brought us the phrase follow the child, as that is how we
BIG IDEA 1: Develop an understanding of and fluency with multiplication and division of fractions and decimals BIG IDEA 1:
 BIG IDEA 1: Develop an understanding of and fluency with multiplication and division of fractions and decimals Multiplying and Dividing Decimals Explain the difference between an exact answer and an estimated
BIG IDEA 1: Develop an understanding of and fluency with multiplication and division of fractions and decimals Multiplying and Dividing Decimals Explain the difference between an exact answer and an estimated
Reading and Understanding Whole Numbers
 Reading and Understanding Whole Numbers Student Book Series D Mathletics Instant Workbooks Copyright Contents Series D Reading and Understanding Whole Numbers Topic Looking at whole numbers reading and
Reading and Understanding Whole Numbers Student Book Series D Mathletics Instant Workbooks Copyright Contents Series D Reading and Understanding Whole Numbers Topic Looking at whole numbers reading and
Number & Place Value: Read, write and represent numbers to 100 Learning focus when objects are rearranged the number remains the same.
 Number & Place Value: Read, write and represent numbers to 100 Learning focus when objects are rearranged the number remains the same. Look at the two sets of shapes. Is there the same number of shapes
Number & Place Value: Read, write and represent numbers to 100 Learning focus when objects are rearranged the number remains the same. Look at the two sets of shapes. Is there the same number of shapes
Comparing Numbers on a Place Value Chart
 Comparing Numbers on a Place Value Chart Students will: Objective Identify the place value of specific digits in a number Represent numbers on a place vale chart Utilize place value charts to compare numbers
Comparing Numbers on a Place Value Chart Students will: Objective Identify the place value of specific digits in a number Represent numbers on a place vale chart Utilize place value charts to compare numbers
Sample pages. 3:06 HCF and LCM by prime factors
 number AND INDICES 7 2 = 49 6 8 = 48 Contents 10 2 = 100 9 11 = 99 12 2 = 144 11 1 = 14 8 2 = 64 7 9 = 6 11 2 = 121 10 12 = 120 :01 Index notation Challenge :01 Now that s a google :02 Expanded notation
number AND INDICES 7 2 = 49 6 8 = 48 Contents 10 2 = 100 9 11 = 99 12 2 = 144 11 1 = 14 8 2 = 64 7 9 = 6 11 2 = 121 10 12 = 120 :01 Index notation Challenge :01 Now that s a google :02 Expanded notation
Solving Who Am I? Puzzles. Building Who Am I? Puzzles. t u Who Am I? The product of my digits is 16. The sum of my digits is 8. Who Am I?
 Solving Puzzles The product of my digits is 7. The sum of my digits is 8. My units digit is greater than my tens digit. I am even. My tens digit is. h t u The product of my three digits is 2. h is four
Solving Puzzles The product of my digits is 7. The sum of my digits is 8. My units digit is greater than my tens digit. I am even. My tens digit is. h t u The product of my three digits is 2. h is four
Day 1. Mental Arithmetic Questions KS3 MATHEMATICS. 60 X 2 = 120 seconds. 1 pm is 1300 hours So gives 3 hours. Half of 5 is 2.
 Mental Arithmetic Questions. The tally chart shows the number of questions a teacher asked in a lesson. How many questions did the teacher ask? 22 KS MATHEMATICS 0 4 0 Level 4 Answers Day 2. How many seconds
Mental Arithmetic Questions. The tally chart shows the number of questions a teacher asked in a lesson. How many questions did the teacher ask? 22 KS MATHEMATICS 0 4 0 Level 4 Answers Day 2. How many seconds
4 th Grade Curriculum Map
 4 th Grade Curriculum Map 2017-18 MONTH UNIT/ CONTENT CORE GOALS/SKILLS STANDARDS WRITTEN ASSESSMENTS ROUTINES RESOURCES VOCABULARY September Chapter 1 8 days NUMBERS AND OPERATIONS IN BASE TEN WORKING
4 th Grade Curriculum Map 2017-18 MONTH UNIT/ CONTENT CORE GOALS/SKILLS STANDARDS WRITTEN ASSESSMENTS ROUTINES RESOURCES VOCABULARY September Chapter 1 8 days NUMBERS AND OPERATIONS IN BASE TEN WORKING
Solving Problems. PS1 Use and apply mathematics to solve problems, communicate and reason Year 1. Activities. PS1.1 Number stories 1.
 PS1 Use and apply mathematics to solve problems, communicate and reason Year 1 PS1.1 Number stories 1 PS1.2 Difference arithmagons PS1.3 Changing orders PS1.4 Making shapes PS1.5 Odd or even? PS1.6 Odd
PS1 Use and apply mathematics to solve problems, communicate and reason Year 1 PS1.1 Number stories 1 PS1.2 Difference arithmagons PS1.3 Changing orders PS1.4 Making shapes PS1.5 Odd or even? PS1.6 Odd
Answer Key Lesson 6: Workshop: Factors, Multiples, and Primes
 3 Answer Key Lesson 6: Student Activity Book Number and Multiplication Concepts Questions 1 27 (SAB pp. 61 7) 1. 21 and 99 are both multiples of 3; Possible response: I can make a rectangle that is 3 by
3 Answer Key Lesson 6: Student Activity Book Number and Multiplication Concepts Questions 1 27 (SAB pp. 61 7) 1. 21 and 99 are both multiples of 3; Possible response: I can make a rectangle that is 3 by
Operations and Algebraic Thinking
 Lesson 1 Operations and Algebraic Thinking Name Use Color Tiles to build each array. Write the multiplication sentence for each array. 1. 2. 3. rows of tiles rows of tiles rows of tiles Build each array
Lesson 1 Operations and Algebraic Thinking Name Use Color Tiles to build each array. Write the multiplication sentence for each array. 1. 2. 3. rows of tiles rows of tiles rows of tiles Build each array
E CA AC EA AA AM AP E CA AC EA AA AM AP E CA AC EA AA AM AP E CA AC EA AA AM AP E CA AC EA AA AM AP E CA AC EA AA AM AP
 1 The role of this book. School wide assessment resource instructions. Contents page Pg3 Pg3 E CA AC EA AA AM AP I am learning my addition and subtraction facts to five. Pg4, 5 I am learning my doubles
1 The role of this book. School wide assessment resource instructions. Contents page Pg3 Pg3 E CA AC EA AA AM AP I am learning my addition and subtraction facts to five. Pg4, 5 I am learning my doubles
Define and Diagram Outcomes (Subsets) of the Sample Space (Universal Set)
 12.3 and 12.4 Notes Geometry 1 Diagramming the Sample Space using Venn Diagrams A sample space represents all things that could occur for a given event. In set theory language this would be known as the
12.3 and 12.4 Notes Geometry 1 Diagramming the Sample Space using Venn Diagrams A sample space represents all things that could occur for a given event. In set theory language this would be known as the
Number. Place value. Vocabulary. Raphael has eight digit cards. He uses the cards to make two four-digit numbers. He uses each card only once.
 Cambridge Unive 978-1-107-61859-6 Cambridge Primary Mathematics Stage 6 Emma Low Excerpt More information Number Place value Vocabulary Raphael has eight digit cards. 1 2 3 4 5 6 7 8 million: equal to
Cambridge Unive 978-1-107-61859-6 Cambridge Primary Mathematics Stage 6 Emma Low Excerpt More information Number Place value Vocabulary Raphael has eight digit cards. 1 2 3 4 5 6 7 8 million: equal to
The Parkland Federation. February 2016
 The Parkland Federation February 206 EYFS/KS Calculations: Recording Addition (page of ). Aggregation/combining 2. Augmentation/counting on 3. Counting Contexts: + + + + Pupils physically combining groups
The Parkland Federation February 206 EYFS/KS Calculations: Recording Addition (page of ). Aggregation/combining 2. Augmentation/counting on 3. Counting Contexts: + + + + Pupils physically combining groups
Year 4. Term by Term Objectives. Year 4 Overview. Autumn. Spring Number: Fractions. Summer. Number: Addition and Subtraction.
 Summer Overview Week 1 Week 2 Week 3 Week 4 Week 5 Week 6 Week 7 Week 8 Week 9 Week 10 Week 11 Week 12 Autumn Number: Place Value Number: Addition and Subtraction Number: Multiplication and Division Measurement:
Summer Overview Week 1 Week 2 Week 3 Week 4 Week 5 Week 6 Week 7 Week 8 Week 9 Week 10 Week 11 Week 12 Autumn Number: Place Value Number: Addition and Subtraction Number: Multiplication and Division Measurement:
Mixed Numbers. represent the same amount. They are equivalent. An improper fraction shows an amount greater than 1 whole. is an improper fraction.
 UNIT 5 STUDENT BOOK Mixed Numbers LESSO N Quick Review At At Home Sc h o o l Tyla arranged trapezoids. Her arrangement shows It also shows whole halves of a hexagon: hexagons plus half: and represent the
UNIT 5 STUDENT BOOK Mixed Numbers LESSO N Quick Review At At Home Sc h o o l Tyla arranged trapezoids. Her arrangement shows It also shows whole halves of a hexagon: hexagons plus half: and represent the
GPLMS Revision Programme GRADE 3 Booklet
 GPLMS Revision Programme GRADE 3 Booklet Learner s name: School name: _ Day 1 1. Read carefully: a) The place or position of a digit in a number gives the value of that digit. b) In the number 273, 2,
GPLMS Revision Programme GRADE 3 Booklet Learner s name: School name: _ Day 1 1. Read carefully: a) The place or position of a digit in a number gives the value of that digit. b) In the number 273, 2,
