Skills Practice Skills Practice for Lesson 4.1
|
|
|
- Robyn Collins
- 5 years ago
- Views:
Transcription
1 Skills Prctice Skills Prctice for Lesson.1 Nme Dte Tiling Bthroom Wll Simplifying Squre Root Expressions Vocbulry Mtch ech definition to its corresponding term. 1. n expression tht involves root. rdicnd 2. the symbol b. squre root of number 3. number b such tht b 2 c. simplest form. when the rdicnd of rdicl expression contins d. rdicl sign no fctors tht re perfect squres 5. n expression under rdicl sign e. perfect squre 6. n integer tht cn be written s the squre of some f. rdicl expression other integer Problem Set Clculte the vlue of ech rdicl expression Chpter Skills Prctice 107
2 Simplify ech expression nd write the result in rdicl form Nme the form of 1 tht you would use to simplify ech frction Simplify ech frction Chpter Skills Prctice
3 Nme Dte Given the re A of squre, clculte the length of one side. 35. A cm A 75 m 2 Chpter Skills Prctice 109
4 37. Ingrid covers the floor of squre room with 196 lrge tiles. The re of ech tile is 1 squre foot. Wht is the length of one side of the room? 3. Devon prepres squre grden with n re of 10 squre feet. How much fencing will Devon need for ech side of the grden? 110 Chpter Skills Prctice
5 Skills Prctice Skills Prctice for Lesson.2 Nme Dte Instlling Stellite Dish The Pythgoren Theorem Vocbulry Define ech term in your own words. 1. right tringle 2. legs 3. hypotenuse. Pythgoren Theorem 5. Converse of the Pythgoren Theorem Chpter Skills Prctice 111
6 Problem Set Determine the length of the hypotenuse of ech tringle. Round your nswer to the nerest tenth, if necessry c 6 c. 9. c 10 c Chpter Skills Prctice
7 Nme Dte Determine the length of the unknown leg. Round your nswer to the nerest tenth, if necessry b b 5 Chpter Skills Prctice 113
8 Use the converse of the Pythgoren Theorem to determine whether ech tringle is right tringle. Explin your nswer Chpter Skills Prctice
9 Nme Dte Use the Pythgoren Theorem to clculte ech unknown length. Round your nswer to the nerest tenth, if necessry. 1. Chndr hs ldder tht is 20 feet long. If the top of the ldder reches 16 feet up the side of building, how fr from the building is the bse of the ldder? 19. A scffold hs digonl support bem to strengthen it. If the scffold is 12 feet high nd 5 feet wide, how long must the support bem be? Chpter Skills Prctice 115
10 20. The length of the hypotenuse of right tringle is 0 centimeters. The legs of the tringle re the sme length. How long is ech leg of the tringle? 21. A crpenter props ldder ginst the wll of building. The bse of the ldder is 10 feet from the wll. The top of the ldder is 2 feet from the ground. How long is the ldder? 116 Chpter Skills Prctice
11 Skills Prctice Skills Prctice for Lesson.3 Nme Dte D rfting Equipment Properties of 5º-5º-90º Tringles Vocbulry Explin why ech term correctly describes the figure below isosceles right tringle 2. 5º-5º-90º tringle Problem Set Determine the length of the hypotenuse of ech 5º-5º-90º tringle. Write your nswer s rdicl in simplest form in. c 5 cm c 5. 9 ft 2 in. c 6. 7 km 5 cm c 9 ft 7 km Chpter Skills Prctice 117
12 Determine the lengths of the legs of ech 5º-5º-90º tringle. Write your nswer s rdicl in simplest form cm 12 mi ft 2 m Use the given informtion to nswer ech question. Round your nswer to the nerest tenth, if necessry. 11. Soren is flying kite on the bech. The string forms 5º ngle with the ground. If he hs let out 16 meters of line, how high bove Soren is the kite? 11 Chpter Skills Prctice
13 Nme Dte 12. Meen is picking ornges from the tree in her yrd. She rests 12-foot ldder ginst the tree t 5º ngle. How fr is the top of the ldder from the ground? 13. Emily is building squre bookshelf. She wnts to dd digonl support bem to the bck to strengthen it. The digonl divides the bookshelf into two 5º-5º-90º tringles. If ech side of the bookshelf is feet long, wht must the length of the support bem be? 1. Prospect Prk is squre with side lengths of 512 meters. One of the pths through the prk runs digonlly from the northest corner to the southwest corner, nd divides the prk into two 5º-5º-90º tringles. How long is tht pth? Determine whether the tringle is 5º-5º-90º tringle. Explin how you know Chpter Skills Prctice 119
14 Determine the re of ech tringle mm 120 Chpter Skills Prctice
15 Nme Dte in ft m Chpter Skills Prctice 121
16 Use the given informtion to nswer ech question. 23. Eli is mking mosic using tiles shped like 5º-5º-90º tringles. The length of the hypotenuse of ech tile is 13 centimeters. Wht is the re of ech tile? 2. Bked pit chips re often in the shpe of 5º-5º-90º tringles. Citlyn finds tht the longest side of pit chip in one bg mesures 3 centimeters. Wht is the re of the pit chip? 25. Annik is mking kite in the shpe of 5º-5º-90º tringle. The longest side of the kite is 2 inches. Wht is the re of the piece of fbric needed for the kite? 122 Chpter Skills Prctice
17 Nme Dte 26. A tent hs mesh door tht is shped like 5º-5º-90º tringle. The longest side of the door is 36 inches. Wht is the re of the mesh door? Chpter Skills Prctice 123
18 12 Chpter Skills Prctice
19 Skills Prctice Skills Prctice for Lesson. Nme Dte Finishing Concrete Properties of 30º-60º-90º Tringles Vocbulry Write the term tht best completes ech sttement. 1. A 30º- -90º tringle is formed by dividing n tringle in hlf by its ltitude. 2. The 30º-60º-90º Tringle Theorem sttes tht the length of the hypotenuse is times the length of the shorter leg, nd the length of the longer leg is the length of the shorter leg. times Problem Set Determine the mesure of the indicted interior ngle. 3. B A C. D 30 E G F m ABC m DFE 5. H R J A K S A T m HAK m TRA Given the length of the short leg of 30º-60º-90º tringle, determine the lengths of the long leg nd hypotenuse. Write your nswers s rdicls in simplest form ft 60 c b in. c b Chpter Skills Prctice 125
20 mm b c cm 60 c b 30 Given the length of the hypotenuse of 30º-60º-90º tringle, determine the lengths of the two legs. Write your nswers s rdicls in simplest form m km b 30 b yd b ft b 30 Given the length of the long side of 30º-60º-90º tringle, determine the lengths of the short leg nd hypotenuse. Write your nswers s rdicls in simplest form c 3 in c 11 3 m Chpter Skills Prctice
21 Nme Dte c c mi 30 1 ft c 60 c m 30 1 in. Determine the re of ech 30º-60º-90º tringle. Round your nswer to the nerest tenth, if necessry cm b 30 Chpter Skills Prctice 127
22 km b Universl Sporting Goods sells pennnts in the shpe of 30º-60º-90º tringles. The length of the longest side of ech pennnt is 16 inches. 2. A fctory produces solid drfting tringles in the shpe of 30º-60º-90º tringles. The length of the side opposite the right ngle is 15 centimeters. 12 Chpter Skills Prctice
23 Nme Dte Determine the volume of the right tringulr prism. Round your nswer to the nerest tenth, if necessry ft ft m 30 2 m Chpter Skills Prctice 129
24 27. Ingrid built len-to shelter while cmping in the wilderness. The len-to shelter hs the dimensions shown in the digrm, nd meets the ground t 30º ngle. Wht is the volume of the len-to shelter? 60 5 ft 30 6 ft 2. The roof of Joshu s house meets the front of the house t 60º ngle, forming n ttic in the shpe of 30º-60º-90º tringulr prism. The front of the house is 0 feet wide, nd the length of the roof is 50 feet long the incline, s shown in the digrm. Wht is the volume of the ttic? 50 ft 0 ft 130 Chpter Skills Prctice
25 Skills Prctice Skills Prctice for Lesson.5 Nme Dte Meeting Friends The Distnce Formul Vocbulry Define ech term in your own words. 1. coordinte plne 2. Distnce Formul Problem Set Archeologists mp the loction of ech item they find t dig on 1 foot 1 foot coordinte grid. Clculte the distnce between ech pir of objects on the given coordinte plne. Explin how you found your nswer. 3. Wht is the distnce between the spindle nd the pottery shrd? y spindle pottery shrd x Chpter Skills Prctice 131
26 . Wht is the distnce between the coins nd the spindle? y spindle coins x 5. Wht is the distnce between the beds nd the spindle? y spindle beds x 132 Chpter Skills Prctice
27 Nme Dte 6. Wht is the distnce between the coins nd the pottery shrd? y coins 3 2 pottery shrd x Clculte the distnce between ech pir of coordinte points. Round your nswer to the nerest tenth, if necessry. 7. (3, ) nd (9, 7) Chpter Skills Prctice 133
28 . (, 2) nd (6, ) 9. (1, 3) nd (9, ) 10. (3, 5) nd (7, 2) 11. (, 2) nd (3, 7) 13 Chpter Skills Prctice
29 Nme Dte 12. (5, 2) nd (0, ) 13. (7, ) nd (2, 9) 1. (5, ) nd (1, 7) 15. (0, 9) nd (5, 2) Chpter Skills Prctice 135
30 16. (, 7) nd (, 5) Use the Distnce Formul to clculte the missing vlue of x. Round your nswer to the nerest tenth, if necessry. 17. The distnce between (1, 2) nd (x, 5) is 5 units. 1. The distnce between (9, 1) nd (x, 7) is 10 units. 136 Chpter Skills Prctice
31 Nme Dte 19. The distnce between (x, ) nd (6, 1) is units. 20. The distnce between (x, 6) nd (7, ) is 7 units. Chpter Skills Prctice 137
32 Use the Distnce Formul to clculte the missing vlue of y. Round your nswer to the nerest tenth, if necessry. 21. The distnce between ( 1, ) nd (5, y) is 10 units. 22. The distnce between (0, 3) nd (6, y) is units. 13 Chpter Skills Prctice
33 Nme Dte 23. The distnce between (10, y) nd ( 2, 2) is 13 units. 2. The distnce between ( 1, y) nd (, 7) is 20 units. Chpter Skills Prctice 139
34 10 Chpter Skills Prctice
35 Skills Prctice Skills Prctice for Lesson.6 Nme Dte Tresure Hunt The Midpoint Formul Vocbulry Identify similrities nd differences between the following terms. 1. midpoint nd men 2. Distnce Formul nd Midpoint Formul Problem Set Divers re mpping the re where ship snk. The coordintes of different lndmrks re given. Plot the coordintes of ech lndmrk on the coordinte grid. 3. (2, 9). (7, 3) y 9 y x x Chpter Skills Prctice 11
36 5. (5, 6) 6. (, 0) y y x x Divers re mpping the re where ship snk on coordinte grid. Determine the midpoint between the pir of lndmrks nd plot the midpoint on the grid. 7. Kerry spots the ship s nchor hlfwy between the lighthouse nd the ledge. Wht re the coordintes of the nchor? y 9 7 ledge rocks lighthouse reef x 12 Chpter Skills Prctice
37 Nme Dte. Erik thinks he will find gold brs hlfwy between the lighthouse nd the reef. Wht re the coordintes of the gold brs? y ledge lighthouse rocks reef x 9. Ilon suspects tht there is chest of gold doubloons t the midpoint between the ledge nd the rocks. At wht coordintes does she think they should serch for the chest? y 9 7 ledge rocks lighthouse reef x Chpter Skills Prctice 13
38 10. Rshid finds one of the ship s cnnons hlfwy between the rocks nd the reef. Wht re the coordintes of the cnnon? y ledge lighthouse rocks reef x 11. The divers gree tht the ship s figurehed is locted t the midpoint between the lighthouse nd the rocks. Wht re the coordintes of the figurehed? y 9 7 ledge rocks lighthouse reef x 1 Chpter Skills Prctice
39 Nme Dte 12. The divers decide to strt their next dive hlfwy between the ledge nd the reef. At wht coordintes will they strt their next dive? y ledge lighthouse rocks reef x Determine the midpoint of the line segment tht hs the given points s its endpoints. Then grph the given points nd the midpoint. 13. (2, ) nd (6, 2) 1. (, 0) nd (, 6) y 9 y x x Chpter Skills Prctice 15
40 15. (9, 3) nd (5, 9) 16. (7, 7) nd (1, 3) y y x x Clculte the midpoint of the line segment tht hs the given points s its endpoints. 17. (, 3) nd (, 9) 1. ( 7, 2) nd ( 3, ) 19. ( 2, 5) nd (10, 7) 20. ( 10, ) nd (6, ) 16 Chpter Skills Prctice
41 Nme Dte 21. (7, 6) nd ( 2, 3) 22. ( 1, ) nd (10, 5) 23. (0, 0) nd (9, 7) 2. ( 5, 6) nd (2, 2) 25. (5, 6) nd ( 6, 5) 26. ( 10, 2) nd (, 3) The coordintes of the endpoint of line segment nd its midpoint re given. Determine the coordintes of the other endpoint. 27. endpoint: (0, 2), midpoint: (3, 3) 2. endpoint: (2, 9), midpoint: (5, 6) Chpter Skills Prctice 17
42 29. endpoint: ( 3, ), midpoint: (0, 1) 30. endpoint: ( 3, 5), midpoint: (1.5, 2) 1 Chpter Skills Prctice
c The scaffold pole EL is 8 m long. How far does it extend beyond the line JK?
3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
REVIEW, pages
REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
REVIEW QUESTIONS TOPIC 5 TRIGONOMETRY I FLUENCY
TOPIC 5 TRIGONOMETRY I REVIEW QUESTIONS FLUENCY The most urte mesure for the length of the third side in the tringle elow is: A 4.83 m B 23.3 m C 3.94 m D 2330 mm E 4826 mm 2 Wht is the vlue of x in this
Lesson 6.1 Skills Practice
Lesson 6.1 Skills Practice Name Date Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Vocabulary Match each definition to its corresponding term. 1. A mathematical statement
Translate and Classify Conic Sections
TEKS 9.6 A.5.A, A.5.B, A.5.D, A.5.E Trnslte nd Clssif Conic Sections Before You grphed nd wrote equtions of conic sections. Now You will trnslte conic sections. Wh? So ou cn model motion, s in E. 49. Ke
First Round Solutions Grades 4, 5, and 6
First Round Solutions Grdes 4, 5, nd 1) There re four bsic rectngles not mde up of smller ones There re three more rectngles mde up of two smller ones ech, two rectngles mde up of three smller ones ech,
The Pythagorean Theorem 8.6.C
? LESSON 8.1 The Pythagorean Theorem ESSENTIAL QUESTION Expressions, equations, and relationships 8.6.C Use models and diagrams to explain the Pythagorean Theorem. 8.7.C Use the Pythagorean Theorem...
Unit 1: Chapter 4 Roots & Powers
Unit 1: Chpter 4 Roots & Powers Big Ides Any number tht cn be written s the frction mm, nn 0, where m nd n re integers, is nn rtionl. Eponents cn be used to represent roots nd reciprocls of rtionl numbers.
Squares and Square Roots Algebra 11.1
Squares and Square Roots Algebra 11.1 To square a number, multiply the number by itself. Practice: Solve. 1. 1. 0.6. (9) 4. 10 11 Squares and Square Roots are Inverse Operations. If =y then is a square
Geometric quantities for polar curves
Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
SAMPLE. End of term: TEST A. Year 4. Name Class Date. Complete the missing numbers in the sequences below.
End of term: TEST A You will need penil nd ruler. Yer Nme Clss Dte 2 Complete the missing numers in the sequenes elow. 50 25 00 75 8 30 3 28 2 9 Put irle round two of the shpes elow whih hve 3 shded. 3
Theme: Don t get mad. Learn mod.
FERURY When 1 is divided by 5, the reminder is. nother wy to sy this is opyright 015 The Ntionl ouncil of Techers of Mthemtics, Inc. www.nctm.org. ll rights reserved. This mteril my not be copied or distributed
Student Book SERIES. Patterns and Algebra. Name
E Student Book 3 + 7 5 + 5 Nme Contents Series E Topic Ptterns nd functions (pp. ) identifying nd creting ptterns skip counting completing nd descriing ptterns predicting repeting ptterns predicting growing
TRIGONOMETRIC APPLICATIONS
HPTER TRIGONOMETRI PPLITIONS n ocen is vst expnse tt cn e life-tretening to person wo experiences disster wile oting. In order for elp to rrive on time, it is necessry tt te cost gurd or sip in te re e
Algebra Practice. Dr. Barbara Sandall, Ed.D., and Travis Olson, M.S.
By Dr. Brr Sndll, Ed.D., Dr. Melfried Olson, Ed.D., nd Trvis Olson, M.S. COPYRIGHT 2006 Mrk Twin Medi, Inc. ISBN 978-1-58037-754-6 Printing No. 404042-EB Mrk Twin Medi, Inc., Pulishers Distriuted y Crson-Dellos
1 tray of toffee 1 bar of toffee. 10 In the decimal number, 0 7, the 7 refers to 7 tenths or
Chpter 3 Deciml Numers Do you know wht DECIMAL is? In chpter, we delt with units, s, 0 s nd 00 s. When you tke single unit nd divide it into (or 0 or 00) its, wht we then hve re deciml frctions of whole
Polar Coordinates. July 30, 2014
Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
(1) Primary Trigonometric Ratios (SOH CAH TOA): Given a right triangle OPQ with acute angle, we have the following trig ratios: ADJ
Tringles nd Trigonometry Prepred y: S diyy Hendrikson Nme: Dte: Suppose we were sked to solve the following tringles: Notie tht eh tringle hs missing informtion, whih inludes side lengths nd ngles. When
Square Roots and the Pythagorean Theorem
UNIT 1 Square Roots and the Pythagorean Theorem Just for Fun What Do You Notice? Follow the steps. An example is given. Example 1. Pick a 4-digit number with different digits. 3078 2. Find the greatest
Catty Corner. Side Lengths in Two and. Three Dimensions
Catty Corner Side Lengths in Two and 4 Three Dimensions WARM UP A 1. Imagine that the rectangular solid is a room. An ant is on the floor situated at point A. Describe the shortest path the ant can crawl
Exercise 1-1. The Sine Wave EXERCISE OBJECTIVE DISCUSSION OUTLINE. Relationship between a rotating phasor and a sine wave DISCUSSION
Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
SOLVING TRIANGLES USING THE SINE AND COSINE RULES
Mthemtics Revision Guides - Solving Generl Tringles - Sine nd Cosine Rules Pge 1 of 17 M.K. HOME TUITION Mthemtics Revision Guides Level: GCSE Higher Tier SOLVING TRIANGLES USING THE SINE AND COSINE RULES
How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr.
Common Core Standard: 8.G.6, 8.G.7 How can we organize our data? What other combinations can we make? What do we expect will happen? CPM Materials modified by Mr. Deyo Title: IM8 Ch. 9.2.2 What Is Special
Example. Check that the Jacobian of the transformation to spherical coordinates is
lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
Chapter 8 Practice Test
Chapter 8 Practice Test Multiple Choice Identify the choice that best completes the statement or answers the question. 1. In triangle ABC, is a right angle and 45. Find BC. If you answer is not an integer,
Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions.
Student Outcomes Students apply the Pythagorean Theorem to real world and mathematical problems in two dimensions. Lesson Notes It is recommended that students have access to a calculator as they work
INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS
CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
The Pythagorean Theorem
. The Pythagorean Theorem Goals Draw squares on the legs of the triangle. Deduce the Pythagorean Theorem through exploration Use the Pythagorean Theorem to find unknown side lengths of right triangles
The Pythagorean Theorem is used in many careers on a regular basis. Construction
Applying the Pythagorean Theorem Lesson 2.5 The Pythagorean Theorem is used in many careers on a regular basis. Construction workers and cabinet makers use the Pythagorean Theorem to determine lengths
Lesson: Pythagorean Theorem Lesson Topic: Use Pythagorean theorem to calculate the hypotenuse
Lesson: Pythagorean Theorem Lesson Topic: Use Pythagorean theorem to calculate the hypotenuse Question 1: What is the length of the hypotenuse? ft Question 2: What is the length of the hypotenuse? m Question
Kirchhoff s Rules. Kirchhoff s Laws. Kirchhoff s Rules. Kirchhoff s Laws. Practice. Understanding SPH4UW. Kirchhoff s Voltage Rule (KVR):
SPH4UW Kirchhoff s ules Kirchhoff s oltge ule (K): Sum of voltge drops round loop is zero. Kirchhoff s Lws Kirchhoff s Current ule (KC): Current going in equls current coming out. Kirchhoff s ules etween
Daily Warmup. - x 2 + x x 2 + x Questions from HW?? (7x - 39) (3x + 17) 1. BD bisects ABC. Find the m ABC.
Daily Warmup Questions from HW?? B 1. BD bisects ABC. Find the m ABC. (3x + 17) (7x - 39) C 2. The figure below is a regular polygon. Find the value of x. - x 2 + x + 43 A D 4x 2 + x - 37 3. The measure
Polar coordinates 5C. 1 a. a 4. π = 0 (0) is a circle centre, 0. and radius. The area of the semicircle is π =. π a
Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem
5/6 Lesson: Angles, measurement, right triangle trig, and Pythagorean theorem I. Lesson Objectives: -Students will be able to recall definitions of angles, how to measure angles, and measurement systems
Student Book SERIES. Fractions. Name
D Student Book Nme Series D Contents Topic Introducing frctions (pp. ) modelling frctions frctions of collection compring nd ordering frctions frction ingo pply Dte completed / / / / / / / / Topic Types
Series. Teacher. Numbers
Series B Techer Copyright 2009 3P Lerning. All rights reserved. First edition printed 2009 in Austrli. A ctlogue record for this book is vilble from 3P Lerning Ltd. ISBN 978-1-921860-17-1 Ownership of
Area and Perimeter. Practice 1 Area of a Rectangle. Find the area of each figure. Example. one-inch squares.
Name: Date: Chapter Practice 1 Area of a Rectangle Find the area of each figure. Example There are 3 rows of one-inch squares. Each row has 4 one-inch squares. 3 3 4 5 12 There are 12 one-inch squares
Section 6.1 Law of Sines. Notes. Oblique Triangles - triangles that have no right angles. A c. A is acute. A is obtuse
Setion 6.1 Lw of Sines Notes. Olique Tringles - tringles tht hve no right ngles h is ute h is otuse Lw of Sines - If is tringle with sides,, nd, then sin = sin = sin or sin = sin = sin The miguous se (SS)
Domination and Independence on Square Chessboard
Engineering nd Technology Journl Vol. 5, Prt, No. 1, 017 A.A. Omrn Deprtment of Mthemtics, College of Eduction for Pure Science, University of bylon, bylon, Irq pure.hmed.omrn@uobby lon.edu.iq Domintion
Name Date. Chapter 15 Final Review
Name Date Chapter 15 Final Review Tell whether the events are independent or dependent. Explain. 9) You spin a spinner twice. First Spin: You spin a 2. Second Spin: You spin an odd number. 10) Your committee
ACCELERATED MATHEMATICS CHAPTER 14 PYTHAGOREAN THEOREM TOPICS COVERED: Simplifying Radicals Pythagorean Theorem Distance formula
ACCELERATED MATHEMATICS CHAPTER 14 PYTHAGOREAN THEOREM TOPICS COVERED: Simplifying Radicals Pythagorean Theorem Distance formula Activity 14-1: Simplifying Radicals In this chapter, radicals are going
Yellowknife km Vancouver km NEL
ic tio n Yellowknife Pr e- Pu bl 1566 km 67.3 Vncouver 112 1870 km hpter 3 tio n cute Tringle Trigonometry ic LERNING GOLS You will be ble to develop your sptil sense by Pr e- Pu bl? Using the sine lw
Part I Multiple Choice
Oregon Focus on Lines and Angles Block 3 Practice Test ~ The Pythagorean Theorem Name Period Date Long/Short Term Learning Targets MA.MS.08.ALT.05: I can understand and apply the Pythagorean Theorem. MA.MS.08.AST.05.1:
So Many Possibilities page 1 of 2
Otober Solving Problems Ativities & So Mny Possibilities pge of Use the blnk spe to solve eh problem. Show ll your work inluding numbers, words, or lbeled skethes. Write omplete sentene below your work
UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet
Name Period Date UNIT 6: CONJECTURE AND JUSTIFICATION WEEK 24: Student Packet 24.1 The Pythagorean Theorem Explore the Pythagorean theorem numerically, algebraically, and geometrically. Understand a proof
You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion)
Pre-Test Unit 7: Pythagorean Theorem KEY You may use a calculator. Answer the following questions. (5 pts; partial credit at teacher discretion) 1. What is the IF-THEN statement for the Pythagorean Theorem?
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN. Inventor: Brian L. Baskin
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
Addition Mission: Facts Practice
Addition Mission: Fcts Prctice ++ Tble of Contents Addition Mission: Fcts Prctice Mth Counting Apple Mth Hippity Hop Crunchy Celery Addition Superstr Cherry Mth At the Librry Mth Sld -0 Sunny Summer Mth
Seven Sisters. Visit for video tutorials
Seven Sisters This imge is from www.quiltstudy.org. Plese visit this website for more informtion on Seven Sisters quilt ptterns. Visit www.blocloc.com for video tutorils 1 The Seven Sisters design cn be
Crime Scene Documentation. Crime Scene Documentation. Taking the C.S. What should my notes include. Note Taking 9/26/2013
Crime Scene Documenttion Crime Scene Documenttion Most importnt step in C.S. processing Purpose: permnently record the condition of C.S. & physicl evidence Time consuming Documenter must be orgnized nd
Section 17.2: Line Integrals. 1 Objectives. 2 Assignments. 3 Maple Commands. 1. Compute line integrals in IR 2 and IR Read Section 17.
Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
CS 135: Computer Architecture I. Boolean Algebra. Basic Logic Gates
Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
MEASURE THE CHARACTERISTIC CURVES RELEVANT TO AN NPN TRANSISTOR
Electricity Electronics Bipolr Trnsistors MEASURE THE HARATERISTI URVES RELEVANT TO AN NPN TRANSISTOR Mesure the input chrcteristic, i.e. the bse current IB s function of the bse emitter voltge UBE. Mesure
The Math Learning Center PO Box 12929, Salem, Oregon Math Learning Center
Resource Overview Quntile Mesure: Skill or Concept: 300Q Model the concept of ddition for sums to 10. (QT N 36) Model the concept of sutrction using numers less thn or equl to 10. (QT N 37) Write ddition
LINER MEASURING Made Easy
LINER MESURING Made Easy PHONE: (800) 983-7665 Fax: (888) 834-09 www.poolproducts.com EMIL: customforms@poolproducts.com 54 Newberry Road, East Windsor, T 06088 IMPORTNT: We base our ustom Liner quotes
Unit 5 and 6 Exam (Modules 11 through 15)
Class: Date: Unit 5 and 6 Exam (Modules 11 through 15) Multiple Choice Identify the choice that best completes the statement or answers the question. 1. Find the value of x. Classify the triangle by its
Pythagorean Theorem. 2.1 Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem... 45
Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
ASSEMBLY INSTRUCTIONS
ASSEMBLY INSTRUCTIONS Multi Line 6 x8 255x193x203cm / 100 1 /2 x76 x80 Poly-Tex, Inc. PO Box 458 27725 Dnville Avenue Cstle Rock, MN 55010 We Site: www.poly-tex.com English - 69717 Hoy Greenhouse Service
ACTIVITY: Comparing Measurements
7.5 Scale Drawings proportionally? How can you enlarge or reduce a drawing 1 ACTIVITY: Comparing Measurements Work with a partner. The diagram shows a food court at a shopping mall. Each centimeter in
Section 10.2 Graphing Polar Equations
Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
Student Instruction Sheet: Unit 4 Lesson 1. Pythagorean Theorem
Student Instruction Sheet: Unit 4 Lesson 1 Suggested time: 75 minutes Pythagorean Theorem What s important in this lesson: In this lesson you will learn the Pythagorean Theorem and how to apply the theorem
Unit 6, Activity 1, Measuring Scavenger Hunt
Unit 6, Activity 1, Measuring Scavenger Hunt Name: Measurement Descriptions Object 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Blackline Masters, Mathematics, Grade 7 Page 6-1 Unit 6, Activity 4, Break it Down Name
Lecture 20. Intro to line integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
EE Controls Lab #2: Implementing State-Transition Logic on a PLC
Objective: EE 44 - Controls Lb #2: Implementing Stte-rnsition Logic on PLC ssuming tht speed is not of essence, PLC's cn be used to implement stte trnsition logic. he dvntge of using PLC over using hrdwre
Areas of Tropezoids, Rhombuses, and Kites
102 Areas of Tropezoids, Rhombuses, and Kites MathemaHcs Florida Standards MAFS.912.G-MG.1.1 Use geometric shapes, their measures, and their properties to describe objects. MP1. MP3, MP 4,MP6 Objective
Name Date. Chapter 15 Final Review
Name Date Chapter 15 Final Review Tell whether the events are independent or dependent. Explain. 9) You spin a spinner twice. First Spin: You spin a 2. Second Spin: You spin an odd number. 10) Your committee
Job Sheet 2. Variable Speed Drive Operation OBJECTIVE PROCEDURE. To install and operate a Variable Speed Drive.
Job Sheet 2 Vrible Speed Drive Opertion OBJECTIVE To instll nd operte Vrible Speed Drive. PROCEDURE Before proceeding with this job, complete the sfety check list in Appendix B. 1. On the Vrible Speed
The Discussion of this exercise covers the following points:
Exercise 4 Bttery Chrging Methods EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the different chrging methods nd chrge-control techniques commonly used when chrging Ni-MI
Synchronous Generator Line Synchronization
Synchronous Genertor Line Synchroniztion 1 Synchronous Genertor Line Synchroniztion Introduction One issue in power genertion is synchronous genertor strting. Typiclly, synchronous genertor is connected
NONCLASSICAL CONSTRUCTIONS II
NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat?
Write an equation that can be used to answer the question. Then solve. Round to the nearest tenth if necessary. 1. How far up the tree is the cat? Notice that the distance from the bottom of the ladder
Misty. Sudnow Dot Songs
Sudnow Dot Songs isty T The Dot Song is nottionl system tht depicts voiced chords in wy where the non-music reder cn find these firly redily. But the Dot Song is not intended be red, not s sight reder
6.1 Soon You Will Determine the Right Triangle Connection The Pythagorean Theorem Can That Be Right? 6.3 Pythagoras to the Rescue
Pythagorean Theorem What is the distance from the Earth to the Moon? Don't let drawings or even photos fool you. A lot of them can be misleading, making the Moon appear closer than it really is, which
Convolutional Networks. Lecture slides for Chapter 9 of Deep Learning Ian Goodfellow
Convolutionl Networks Lecture slides for Chpter 9 of Deep Lerning In Goodfellow 2016-09-12 Convolutionl Networks Scle up neurl networks to process very lrge imges / video sequences Sprse connections Prmeter
Whirlygigs for Sale! Rotating Two-Dimensional Figures through Space. LESSON 4.1 Skills Practice. Vocabulary. Problem Set
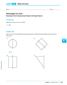LESSON.1 Skills Practice Name Date Whirlygigs for Sale! Rotating Two-Dimensional Figures through Space Vocabulary Describe the term in your own words. 1. disc Problem Set Write the name of the solid figure
The Real Number System and Pythagorean Theorem Unit 9 Part B
The Real Number System and Pythagorean Theorem Unit 9 Part B Standards: 8.NS.1 Know that numbers that are not rational are called irrational. Understand informally that every number has a decimal expansion;
Grade 8 The Pythagorean Theorem
THE NEWARK PUBLIC SCHOOLS THE OFFICE OF MATHEMATICS Grade 8 The Pythagorean Theorem 8.G.6-8 Student Pages Grade 8 - Lesson 1 Introductory Task Introductory Task Prerequisite Competencies 8.EE.2 Use square
Representing Square Numbers. Use materials to represent square numbers. A. Calculate the number of counters in this square array.
1.1 Student book page 4 Representing Square Numbers You will need counters a calculator Use materials to represent square numbers. A. Calculate the number of counters in this square array. 5 5 25 number
Honors Geometry Summer Math Packet
Honors Geometry Summer Math Packet Dear students, The problems in this packet will give you a chance to practice geometry-related skills from Grades 6 and 7. Do your best to complete each problem so that
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
SPECIAL EDITION. Spring 2012 Ezine. where crafty is contagious
Spring 2012 Ezine SPECIAL EDITION www.clubchiccircle.com where crfty is contgious shmrock sttionery It is so esy to mke these festive homemde crds! Mke homemde stmp from the end of n pencil erser. With
Geometry. Warm Ups. Chapter 11
Geometry Warm Ups Chapter 11 Name Period Teacher 1 1.) Find h. Show all work. (Hint: Remember special right triangles.) a.) b.) c.) 2.) Triangle RST is a right triangle. Find the measure of angle R. Show
9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations
54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
Length and area Block 1 Student Activity Sheet
Block 1 Student Activity Sheet 1. Write the area and perimeter formulas for each shape. 2. What does each of the variables in these formulas represent? 3. How is the area of a square related to the area
Math 11 Essentials Intro to Geometry
Math 11 Essentials Intro to Geometry 1. Exponents are numbers located to the upper right of a number that tell you how many factors of that number you have. For example, 5 3 means there are two factors
SECOND EDITION STUDENT BOOK GRADE
SECOND EDITION STUDENT BOOK GRADE 5 Bridges in Mthemtics Second Edition Grde 5 Student Book Volumes 1 & 2 The Bridges in Mthemtics Grde 5 pckge consists of: Bridges in Mthemtics Grde 5 Techers Guide Units
Regular languages can be expressed as regular expressions.
Regulr lnguges cn e expressed s regulr expressions. A generl nondeterministic finite utomton (GNFA) is kind of NFA such tht: There is unique strt stte nd is unique ccept stte. Every pir of nodes re connected
Synchronous Machine Parameter Measurement
Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
GRADE SECOND EDITION HOME CONNECTIONS ANSWER KEY
HOME CONNECTIONS SECOND EDITION ANSWER KEY GRADE 4 Bridges in Mthemtics Second Edition Grde 4 Home Connections Volumes 1 & 2 The Bridges in Mthemtics Grde 4 pckge consists of: Bridges in Mthemtics Grde
Assignment Assignment for Lesson 3.1
Assignment Assignment for Lesson.1 Name Date Weaving a Rug Area and Perimeter of Rectangles and Squares 1. An artist is weaving a rectangular rug to match the pattern shown in the figure. Use the figure
Patterns and Algebra
Student Book Series D Mthletis Instnt Workooks Copyright Series D Contents Topi Ptterns nd funtions identifying nd reting ptterns skip ounting ompleting nd desriing ptterns numer ptterns in tles growing
Geometry 2001 part 1
Geometry 2001 part 1 1. Point is the center of a circle with a radius of 20 inches. square is drawn with two vertices on the circle and a side containing. What is the area of the square in square inches?
SECOND EDITION HOME CONNECTIONS GRADE
SECOND EDITION HOME COECTIONS GRADE 4 Bridges in Mthemtics Second Edition Grde 4 Home Connections Volumes 1 & 2 The Bridges in Mthemtics Grde 4 pckge consists of: Bridges in Mthemtics Grde 4 Techers Guide
University of Houston High School Mathematics Contest Geometry Exam Spring 2016
University of Houston High School Mathematics ontest Geometry Exam Spring 016 nswer the following. Note that diagrams may not be drawn to scale. 1. In the figure below, E, =, = 4 and E = 0. Find the length
11.2 Areas of Trapezoids,
11. Areas of Trapezoids, Rhombuses, and Kites Goal p Find areas of other types of quadrilaterals. Your Notes VOCABULARY Height of a trapezoid THEOREM 11.4: AREA OF A TRAPEZOID b 1 The area of a trapezoid
8-1 Similarity in Right Triangles
8-1 Similarity in Right Triangles In this chapter about right triangles, you will be working with radicals, such as 19 and 2 5. radical is in simplest form when: 1. No perfect square factor other then
Math Circles Finite Automata Question Sheet 3 (Solutions)
Mth Circles Finite Automt Question Sheet 3 (Solutions) Nickols Rollick nrollick@uwterloo.c Novemer 2, 28 Note: These solutions my give you the nswers to ll the prolems, ut they usully won t tell you how
Essential Mathematics Practice Problems for Exam 5 Chapter 8
Math 254B Essential Mathematics Practice Problems for Eam 5 Chapter 8 Name Date This eam is closed book and closed notes, ecept for the Geometry Formula sheet that is provided by the instructor. You can
1. Convert 60 mi per hour into km per sec. 2. Convert 3000 square inches into square yards.
ACT Practice Name Geo Unit 3 Review Hour Date Topics: Unit Conversions Length and Area Compound shapes Removing Area Area and Perimeter with radicals Isosceles and Equilateral triangles Pythagorean Theorem
Boo to You Mystery Quilt FORT WORTH FABRIC STUDIO -- DESIGNED BY: LINDSEY WEIGHT
his sew long will lst five weeks. Boo to You Mystery Quilt R WR BR U -- GN BY: NY WG will include P downlod ech week so you cn esily print off the instructions for ech block. www.fortworthfbricstudio.blogspot.com