Determining MTF with a Slant Edge Target ABSTRACT AND INTRODUCTION
|
|
|
- Imogen Poole
- 6 years ago
- Views:
Transcription
1 Determining MTF with a Slant Edge Target Douglas A. Kerr Issue 2 October 13, 2010 ABSTRACT AND INTRODUCTION The modulation transfer function (MTF) of a photographic lens tells us how effectively the lens transfers a luminance variation in the scene (by which detail is conveyed) onto the focal plane, and in particular how that varies with spatial frequency (which we can think of as the fineness of the detail). This function indicates, objectively, the resolving potential of the lens. We often read of the MTF being determined using a slant edge target test. In this article we review the concept of the MTF and the principles of this testing technique. THE MODULATION TRANSFER FUNCTION We will examine the concept of the modulation transfer function by looking in sequence at the three words that make up its description. Modulation Modulation in this case refers to the variation in the luminance of a scene from point to point, and the corresponding variation in the illuminance from point to point in the image deposited by the lens on the focal plane (on the film or digital sensor). Detail is conveyed by such variation; if there is no variation in luminance, the scene is uniform gray and hardly worth photographing. 1 Modulation can be quantified in terms of modulation depth, a way of expressing the ratio between the maximum and minimum luminance (or illuminance) across a certain small part of the scene (or image). Transfer For our purposes here, the job of the lens is to transfer the luminance variation of the scene into an illuminance variation on the image. It does this incompletely, for various reasons. We can quantify the degree to which it accomplishes this job in terms of the modulation transfer ratio. This is the ratio of (a) the modulation depth of the 1 For the sake of simplicity, we will assume only monochrome scenes and gray scale photography, so that luminance/illuminance is the only property of interest. Copyright 2010 Douglas A. Kerr. May be reproduced and/or distributed but only intact, including this notice. Brief excerpts may be reproduced with credit.
2 Determining MTF with a Slant Edge Target Page 2 illuminance deposited on the image to (b) the modulation depth of the luminance of the scene (usually within a small region). The modulation transfer ratio is quite parallel to the gain of an amplifier stage in an electronic system. Function In mathematics, when the value of one variable quantity depends on the value(s) of one or more other variable quantities, in some specific way, the first variable is said to be a function of the other variable(s). Under this concept, we may say that x is a function of y and z. That means that the value of variable x (called the dependent variable) is determined by the values of variables y and z (called the independent variables). A specific name identifying a function can, in common practice, mean three distinct things: The variable x itself (after all, we said x is a function... ). The value of x for a certain set of values of the independent variables (the value of the function for that situation). The overall relationship by which x depends on y and z (the function proper). This diverse use of the function name can be confusing if we have not been forewarned about it. Graphic representation of a function If a variable is a function of one other variable ( x is a function of y ), we can show the relationship graphically in the familiar way a plot of x against y. If one variable is a function of two other variables ( x is a function of y and z ), we cannot show the relationship graphically in the familiar way. Often what we will do then is to take one of the independent variables and (arbitrarily) consider it to be a parameter (it is still an independent variable; we just handle it a little differently). Suppose we decide to treat z as the parameter. We adopt some specific value of z and, holding that constant, plot the variation of x with y (labeling the curve with the value of z). Then we take another specific value of z and, holding that constant, again plot the variation of x with y (labeling that curve with the new value of z).
3 Determining MTF with a Slant Edge Target Page 3 The result is what we often describe as a family of curves, one curve for each of our chosen values of the parameter, z. But we can equally legitimately decide to treat y as a parameter. Then we choose a certain value of y and, holding that constant, plot the variation of x with z, and so forth. Which of those we do will depend on the context in which we wish to visualize the variation of x. The modulation transfer function For a given lens with a given aperture (and focal length setting, if relevant), the modulation transfer ratio varies with several factors, most prominently: The spatial frequency 2 of the modulation (which we can think of as the fineness of the detail the modulation conveys). Typically the modulation transfer ratio decreases as the spatial frequency increases. The location in the image of the area of interest (notably its distance from the optical axis of the lens. Typically the modulation transfer ratio decreases as we move from the optical axis. Thus, the modulation transfer ratio is a function of spatial frequency and distance off axis. This function is called the modulation transfer function (MTF) of the lens. And of course, as we discussed earlier, the term MTF is also applied to the modulation transfer ratio (which we then never hear of under its own name), or to its value in a particular situation. Two presentations As we mentioned above, when a variable is a function of two other variables, there are two ways to present the relationship graphically, choosing either of the two independent variables to play the role of a parameter. For scientific or optical engineering work with the MTF, we normally select distance off the axis as the parameter, and plot the modulation transfer ratio against spatial frequency (preferably in cycles/mm). But, 2 Spatial frequency has dimensions of cycles per unit distance. In scientific work, the unit is typically cycles per millimeter. Often this unit is spoken of in optical work as line pairs per mm, but sometimes as lines per mm, a source of considerable confusion. There are historical justifications for both these conflicting practices; these are beyond the scope of this article.
4 Determining MTF with a Slant Edge Target Page 4 given the dual use of the term MTF, we are almost forced to say, we select distance off the axis as the parameter, and plot MTF against spatial frequency. In other words, this form of the MTF is a plot of MTF against spatial frequency. However, when MTF data is presented by lens manufacturers, they customarily select spatial frequency as the parameter, and plot the MTF (meaning the modulation transfer ratio) against distance off axis. Usually, there are only two curves, for a low and a not so low spatial frequency. 3 DETERMINING THE MODULATION TRANSFER RATIO The classical concept The classical concept of determining the MTF of a lens involves presenting it with patterns having repetitive variations in luminance (of a known modulation depth) at different spatial frequencies. Then, the pattern deposited on the focal plane is examined (perhaps with a special instrument, or perhaps by capturing it with precisely calibrated film) and noting the modulation depth for each test pattern. We make this determination both at the center of the image and then at locations at successively greater distances from the axis. The two modulation depths, for each combination of spatial frequency and distance off axis, are compared to get the modulation transfer ratio. This is then plotted against the appropriate non-parameter independent variable for the desired form of presentation. Although in the form of the MTF curves presented by lens manufacturers often only two spatial frequencies are treated, for scientific work it is important that we have the MTF at numerous spatial frequencies. Doing so requires test exposures done with numerous test targets, each having patterns of lines at various spacings. A more modern method The availability of computers to easily perform sophisticated manipulation of data, and the fact that a digital camera inherently has an instrument for measuring illuminance the focal plane (its sensor), have led to the adoption of a quite different technique for determining the MTF of a lens, the slant edge target technique. This technique is the actual subject of this article. 3 Actually, there are often eight curves, accommodating two values of the parameters aperture and modulation axis.
5 Determining MTF with a Slant Edge Target Page 5 THE SLANT EDGE TARGET TECHNIQUE CONCEPT An analog in electrical engineering The underlying concept of the technique can perhaps be most clearly seen by considering an electrical engineering example. The MTF (in the sense of a plot of modulation transfer ratio against spatial frequency) is quite parallel to the matter of the frequency response of an electronic amplifier, where we plot the gain of the amplifier (the ratio of the output voltage to the input voltage) as a function of frequency (in this case temporal frequency, in hertz). Not surprisingly, the classical technique for determining the frequency response (we can call it the gain function ) involves presenting the amplifier with signals of known voltage at different frequencies, and in each case, measuring the output power. The plot of the gain (ratio of output voltage to input voltage) against frequency is the voltage gain function. But there is a way to determine this with a one shot test (and the term is very apt). We submit to the amplifier what is called an impulse, a single pulse which (ideally) has zero duration (zero width) but still contains energy. When we do this, a certain waveform comes out of the amplifier. It is called the impulse response of the amplifier. If we capture that (just one test is needed), we can from it determine the entire voltage gain function (gain as a function of frequency). How can this be? Well, the impulse contains energy at all frequencies (in theory, up to infinity), with a uniform distribution. If we take the Fourier transform 4 of the output waveform, the result is a description of the frequency content of that waveform. And, given that the input signal contains all frequencies, uniformly, that description will be the voltage gain function (or voltage frequency response ). Well, clever as this sounds on paper, there are some practical problems with actually doing it. One is that our impulse, if it is truly to have a zero duration (zero width in time) but nevertheless contain some energy (and of course, if it didn t there would be no output from it), it must (theoretically) have infinite amplitude (voltage). Let s be thankful we can t actually do this; if we could, our amplifier would blow up during the test. 4 A mathematical process that takes a description of a waveform and from it develops a description of its frequency content.
6 Determining MTF with a Slant Edge Target Page 6 And making a pulse have zero width isn t possible either. So we resort to a variation of the theme. Here, instead of using an impulse as our input we use a step function. This is a waveform that, for example, starts out at +1.0 volt and then, at a certain point in time, instantaneously changes to 1.0 volt. Again this is not possible to actually achieve, but it is a lot easier to approximate than an impulse with zero time width and infinite voltage. After applying this (just once) to our amplifier, and capturing the output waveform, we then take the Fourier transform of that. The result, as before, will be the frequency response (gain function) of the amplifier (although in this case, it is in terms of power gain rather than voltage gain). Now, back to optics If we present a zero-width bright line to a lens, it is the optical equivalent of the impulse in the electrical situation. Unless the lens has infinite resolution, the image of that line on the focal plane will be a pattern having non-zero width, across which the illuminance varies in some way. This is called the line spread function (LSF) of the lens. If we take its Fourier transform, we get what turns out to be the square root of the modulation transfer ratio as a function of spatial frequency: the modulation transfer function (MTF). But of course, just as for the electrical impulse, this zero width line is impractical to make, and for it to have enough photometric energy that we can see the pattern of illuminance on the focal plane, it would have to have essentially infinite luminance. So we follow the same ploy used in the electrical situation. We use a test scene that is black up to a straight line boundary and white beyond it the optical equivalent of the electrical step function. For any real lens, the image of that test scene will not have a zero width boundary between dark and light regions, but rather a boundary of some finite width, across which the illuminance varies in some way. The plot of illuminance across that boundary is called the edge spread function (ESF) of the lens. If we measure this illuminance pattern take its Fourier transform, we get the modulation transfer ratio as a function of spatial frequency: the modulation transfer function (MTF). Wow! Is this neat or what!
7 Determining MTF with a Slant Edge Target Page 7 THE REALITIES The need In order to do this, for MTFs of the kind we fortunately encounter with modern lenses, we have to be able to measure the illuminance pattern the edge spread function with very high resolution. Of course, a practical advantage of this technique is that we can use the camera sensor itself to measure the illuminance pattern. But the theoretical resolution of the sensor array is not sufficient to discern the illuminance pattern with sufficient resolution. We see this illustrated in Figure 1. a. b. c. d. Figure 1. Resolving the edge spread function
8 Determining MTF with a Slant Edge Target Page 8 In panel a, we see a hypothetical edge spread function (as would be observed downstream from the lens under test). The gray grid is at the pixel pitch of the camera sensor array, in order to give an idea of the scale. In panel b, we see what would happen if the edge image was located in a certain way on the pixel grid. (We only consider pixels along a line perpendicular to the boundary). The plot line across the band for each pixel shows the pixel output (only a single value for any pixel, of course). Note that the overall sensor output for this row of pixels seems to be a perfect step function (in electrical terms). In panel c, we see a slightly different location of the image. Now we see a different pixel output still certainly not a precise representation of the illuminance pattern itself. In panel d, we see yet another possibility again not even close to a precise representation of the illuminance pattern. So regardless of which one of these happens and this is essentially beyond our control the illuminance pattern suggested by the sensor output is useless for precise analysis. So we must fake enhanced resolution of the sensor. The slant edge target Enter now the title character of this drama. As before, we present the lens with a target with a black portion and a white portion, with a sharp boundary between. But we intentionally orient it so that the boundary does not match the pixel axis of the sensor array, by a small angle. Now, a fascinating drama can play out; we can follow it on Figure 2. We see the image of the target laid out on the sensor pixel detector grid. (The black portion is shown in gray to allow the entire grid to be seen.) Each square represents the domain of one pixel detector. But we will assume that each detector actually only responds to the illuminance at the center of its domain (where we will show a dot if we are interested in the output of that detector). The variation in illuminance (the edge spread function) happens along the ESF axis direction, and of course it happens identically all across the edge. That is, the illuminance will be constant along any line parallel to the boundary (a certain distance from the edge); the variation in illuminance will be the same along any line parallel to the ESF axis (which is drawn in an arbitrary location).
9 Determining MTF with a Slant Edge Target Page 9 Target image Pixel grid Pixels considered a. ESF axis Target image Pixel grid b. Pixels considered ESF axis Figure 2. Operation of the slant edge target We first consider the response of the line of pixel detectors (hereafter, just pixels ) highlighted in panel a. These pixels pick up the luminance of the edge spread pattern at various distances from the boundary, which are evenly spaced. That illuminance is the same all along the associated dotted line, drawn parallel to the boundary. Thus a measurement taken at any point along such a line represents the
10 Determining MTF with a Slant Edge Target Page 10 illuminance every place along it (including where the line crosses our arbitrarily-drawn ESF axis, along which we are interested in the variation of illuminance). The reason we have only concentrated on one row of pixels in this panel is not because they have any special role, but merely because if we started by considering all the pixels, the drawing would have been so busy that it might have been hard to grasp the principle from it. But now that we know what we are looking for, in panel b we consider the response of all the pixels over a larger region. Recall that the output of any pixel represents the illuminance any place along a line parallel to the boundary. Thus we have again drawn the lines parallel to the boundary through each pixel point. The illuminance is the same along any of these lines. We ve not drawn them dotted as that is just too busy for this already-too-busy drawing. But we have drawn slightly bolder the ones shown in panel a. We see now that the suite of output data from all these pixels has told us the luminance along each of many lines parallel to the boundary, and very closely (and evenly) spaced. These values are in fact the luminance at points with that particular spacing along our arbitrarily-drawn ESF axis. Accordingly, this suite of data gives us a high-resolution description of the variation of illuminance along the ESF axis; that is, a high-resolution description of the ESF itself, which we require to make a precise determination of the MTF. The spacing of the samples of the ESF is in fact the pixel pitch multiplied by the sine of the angle of rotation of the target. In our illustration (where the rotation is about ), this is a little less than one-fifth the pixel pitch. Thus, our clever approach gives us an effective resolution of about five times that which could be given by the sensor array in normal use. Because the pixel detectors actually do not pick up the luminance at a point (as suggested by our example), but rather respond to an average of some sort over a region approaching the domain of the pixel, certain special steps have to be taken in the evaluation of the edge 5 This is a greater angle than that usually used for such tests, adopted here for clarity of the illustration. One widely used test target uses an angle of about 5.7, specifically a slope (tangent of the angle) of 1:10. The tidy repetitive pattern of sample distances we see in the example requires an angle whose tangent is a ratio of integers, preferably 1/n.
11 Determining MTF with a Slant Edge Target Page 11 spread function from the set of collected pixel detector values. This is a well-known matter in digital signal processing. Note that the axis along which the edge spread function is considered (by definition, perpendicular to the edge ) is not either axis of the pixel array. This is not really of any consequence to us; the edge spread function exists in two dimensional space regardless of the orientation of the target. 6 Target orientation Any given scheme for determining the MTF with the slant edge technique will have an intended rotation of the target edge. However, we cannot always assure that this angle is exactly achieved. MTF analysis software for use with the slanted edge target technique typically contains provisions for first deducing the exact rotation of the target edge from the data (you can visualize from Figure 2 how this generally could work) and then using the result in the actual analysis. SUMMARY The slant edge target approach allows a convenient one-shot determination of the MTF (in the sense of the modulation transfer ratio as a function of spatial frequency) by exploiting two clever ploys: The use of the Fourier transfer to get the MTF from the edge spread function. The use of the slanted target to get an effective resolution of the sensor array much greater than would be dictated by its pixel pitch so that the edge spread function can be adequately measured by the sensor array itself. # 6 Actually, when we get into one of the esoteric subtleties of the MTF (the matter of axis of modulation ), the direction of the ESF axis is of concern. We can deal with that by thoughtful choice of at what points in the image (at different distances from the center) do we run tests.
The Hemispherical Receptor Incident Light Exposure Meter
 The Hemispherical Receptor Incident Light Exposure Meter Douglas A. Kerr Issue 2 August 5, 2014 ABSTRACT Incident light exposure metering is a useful technique for planning photographic exposure in many
The Hemispherical Receptor Incident Light Exposure Meter Douglas A. Kerr Issue 2 August 5, 2014 ABSTRACT Incident light exposure metering is a useful technique for planning photographic exposure in many
Defense Technical Information Center Compilation Part Notice
 UNCLASSIFIED Defense Technical Information Center Compilation Part Notice ADPO 11345 TITLE: Measurement of the Spatial Frequency Response [SFR] of Digital Still-Picture Cameras Using a Modified Slanted
UNCLASSIFIED Defense Technical Information Center Compilation Part Notice ADPO 11345 TITLE: Measurement of the Spatial Frequency Response [SFR] of Digital Still-Picture Cameras Using a Modified Slanted
ISO INTERNATIONAL STANDARD. Photography Electronic still-picture cameras Resolution measurements
 INTERNATIONAL STANDARD ISO 12233 First edition 2000-09-01 Photography Electronic still-picture cameras Resolution measurements Photographie Appareils de prises de vue électroniques Mesurages de la résolution
INTERNATIONAL STANDARD ISO 12233 First edition 2000-09-01 Photography Electronic still-picture cameras Resolution measurements Photographie Appareils de prises de vue électroniques Mesurages de la résolution
Be aware that there is no universal notation for the various quantities.
 Fourier Optics v2.4 Ray tracing is limited in its ability to describe optics because it ignores the wave properties of light. Diffraction is needed to explain image spatial resolution and contrast and
Fourier Optics v2.4 Ray tracing is limited in its ability to describe optics because it ignores the wave properties of light. Diffraction is needed to explain image spatial resolution and contrast and
Optical Performance of Nikon F-Mount Lenses. Landon Carter May 11, Measurement and Instrumentation
 Optical Performance of Nikon F-Mount Lenses Landon Carter May 11, 2016 2.671 Measurement and Instrumentation Abstract In photographic systems, lenses are one of the most important pieces of the system
Optical Performance of Nikon F-Mount Lenses Landon Carter May 11, 2016 2.671 Measurement and Instrumentation Abstract In photographic systems, lenses are one of the most important pieces of the system
ECEN 4606, UNDERGRADUATE OPTICS LAB
 ECEN 4606, UNDERGRADUATE OPTICS LAB Lab 2: Imaging 1 the Telescope Original Version: Prof. McLeod SUMMARY: In this lab you will become familiar with the use of one or more lenses to create images of distant
ECEN 4606, UNDERGRADUATE OPTICS LAB Lab 2: Imaging 1 the Telescope Original Version: Prof. McLeod SUMMARY: In this lab you will become familiar with the use of one or more lenses to create images of distant
digital film technology Resolution Matters what's in a pattern white paper standing the test of time
 digital film technology Resolution Matters what's in a pattern white paper standing the test of time standing the test of time An introduction >>> Film archives are of great historical importance as they
digital film technology Resolution Matters what's in a pattern white paper standing the test of time standing the test of time An introduction >>> Film archives are of great historical importance as they
Introduction. Chapter Time-Varying Signals
 Chapter 1 1.1 Time-Varying Signals Time-varying signals are commonly observed in the laboratory as well as many other applied settings. Consider, for example, the voltage level that is present at a specific
Chapter 1 1.1 Time-Varying Signals Time-varying signals are commonly observed in the laboratory as well as many other applied settings. Consider, for example, the voltage level that is present at a specific
E X P E R I M E N T 12
 E X P E R I M E N T 12 Mirrors and Lenses Produced by the Physics Staff at Collin College Copyright Collin College Physics Department. All Rights Reserved. University Physics II, Exp 12: Mirrors and Lenses
E X P E R I M E N T 12 Mirrors and Lenses Produced by the Physics Staff at Collin College Copyright Collin College Physics Department. All Rights Reserved. University Physics II, Exp 12: Mirrors and Lenses
Physics 3340 Spring Fourier Optics
 Physics 3340 Spring 011 Purpose Fourier Optics In this experiment we will show how the Fraunhofer diffraction pattern or spatial Fourier transform of an object can be observed within an optical system.
Physics 3340 Spring 011 Purpose Fourier Optics In this experiment we will show how the Fraunhofer diffraction pattern or spatial Fourier transform of an object can be observed within an optical system.
APPLICATIONS FOR TELECENTRIC LIGHTING
 APPLICATIONS FOR TELECENTRIC LIGHTING Telecentric lenses used in combination with telecentric lighting provide the most accurate results for measurement of object shapes and geometries. They make attributes
APPLICATIONS FOR TELECENTRIC LIGHTING Telecentric lenses used in combination with telecentric lighting provide the most accurate results for measurement of object shapes and geometries. They make attributes
Evaluating Commercial Scanners for Astronomical Images. The underlying technology of the scanners: Pixel sizes:
 Evaluating Commercial Scanners for Astronomical Images Robert J. Simcoe Associate Harvard College Observatory rjsimcoe@cfa.harvard.edu Introduction: Many organizations have expressed interest in using
Evaluating Commercial Scanners for Astronomical Images Robert J. Simcoe Associate Harvard College Observatory rjsimcoe@cfa.harvard.edu Introduction: Many organizations have expressed interest in using
Fast MTF measurement of CMOS imagers using ISO slantededge methodology
 Fast MTF measurement of CMOS imagers using ISO 2233 slantededge methodology M.Estribeau*, P.Magnan** SUPAERO Integrated Image Sensors Laboratory, avenue Edouard Belin, 34 Toulouse, France ABSTRACT The
Fast MTF measurement of CMOS imagers using ISO 2233 slantededge methodology M.Estribeau*, P.Magnan** SUPAERO Integrated Image Sensors Laboratory, avenue Edouard Belin, 34 Toulouse, France ABSTRACT The
CAMERA BASICS. Stops of light
 CAMERA BASICS Stops of light A stop of light isn t a quantifiable measurement it s a relative measurement. A stop of light is defined as a doubling or halving of any quantity of light. The word stop is
CAMERA BASICS Stops of light A stop of light isn t a quantifiable measurement it s a relative measurement. A stop of light is defined as a doubling or halving of any quantity of light. The word stop is
Name: Date: Math in Special Effects: Try Other Challenges. Student Handout
 Name: Date: Math in Special Effects: Try Other Challenges When filming special effects, a high-speed photographer needs to control the duration and impact of light by adjusting a number of settings, including
Name: Date: Math in Special Effects: Try Other Challenges When filming special effects, a high-speed photographer needs to control the duration and impact of light by adjusting a number of settings, including
Physics 23 Laboratory Spring 1987
 Physics 23 Laboratory Spring 1987 DIFFRACTION AND FOURIER OPTICS Introduction This laboratory is a study of diffraction and an introduction to the concepts of Fourier optics and spatial filtering. The
Physics 23 Laboratory Spring 1987 DIFFRACTION AND FOURIER OPTICS Introduction This laboratory is a study of diffraction and an introduction to the concepts of Fourier optics and spatial filtering. The
Tangents. The f-stops here. Shedding some light on the f-number. by Marcus R. Hatch and David E. Stoltzmann
 Tangents Shedding some light on the f-number The f-stops here by Marcus R. Hatch and David E. Stoltzmann The f-number has peen around for nearly a century now, and it is certainly one of the fundamental
Tangents Shedding some light on the f-number The f-stops here by Marcus R. Hatch and David E. Stoltzmann The f-number has peen around for nearly a century now, and it is certainly one of the fundamental
Exposure Control in the Canon Wireless Flash System
 70 th birthday series Exposure Control in the Canon Wireless Flash System Douglas A. Kerr, P.E. Issue 2 May 12, 2006 ABSTRACT The Canon Wireless Flash System allows freestanding Canon Speedlite flash units
70 th birthday series Exposure Control in the Canon Wireless Flash System Douglas A. Kerr, P.E. Issue 2 May 12, 2006 ABSTRACT The Canon Wireless Flash System allows freestanding Canon Speedlite flash units
AC phase. Resources and methods for learning about these subjects (list a few here, in preparation for your research):
 AC phase This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
AC phase This worksheet and all related files are licensed under the Creative Commons Attribution License, version 1.0. To view a copy of this license, visit http://creativecommons.org/licenses/by/1.0/,
The Noise about Noise
 The Noise about Noise I have found that few topics in astrophotography cause as much confusion as noise and proper exposure. In this column I will attempt to present some of the theory that goes into determining
The Noise about Noise I have found that few topics in astrophotography cause as much confusion as noise and proper exposure. In this column I will attempt to present some of the theory that goes into determining
The Bellows Extension Exposure Factor: Including Useful Reference Charts for use in the Field
 The Bellows Extension Exposure Factor: Including Useful Reference Charts for use in the Field Robert B. Hallock hallock@physics.umass.edu revised May 23, 2005 Abstract: The need for a bellows correction
The Bellows Extension Exposure Factor: Including Useful Reference Charts for use in the Field Robert B. Hallock hallock@physics.umass.edu revised May 23, 2005 Abstract: The need for a bellows correction
IMAGE FORMATION. Light source properties. Sensor characteristics Surface. Surface reflectance properties. Optics
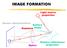 IMAGE FORMATION Light source properties Sensor characteristics Surface Exposure shape Optics Surface reflectance properties ANALOG IMAGES An image can be understood as a 2D light intensity function f(x,y)
IMAGE FORMATION Light source properties Sensor characteristics Surface Exposure shape Optics Surface reflectance properties ANALOG IMAGES An image can be understood as a 2D light intensity function f(x,y)
Experiment 1: Fraunhofer Diffraction of Light by a Single Slit
 Experiment 1: Fraunhofer Diffraction of Light by a Single Slit Purpose 1. To understand the theory of Fraunhofer diffraction of light at a single slit and at a circular aperture; 2. To learn how to measure
Experiment 1: Fraunhofer Diffraction of Light by a Single Slit Purpose 1. To understand the theory of Fraunhofer diffraction of light at a single slit and at a circular aperture; 2. To learn how to measure
8.2 IMAGE PROCESSING VERSUS IMAGE ANALYSIS Image processing: The collection of routines and
 8.1 INTRODUCTION In this chapter, we will study and discuss some fundamental techniques for image processing and image analysis, with a few examples of routines developed for certain purposes. 8.2 IMAGE
8.1 INTRODUCTION In this chapter, we will study and discuss some fundamental techniques for image processing and image analysis, with a few examples of routines developed for certain purposes. 8.2 IMAGE
FRAUNHOFER AND FRESNEL DIFFRACTION IN ONE DIMENSION
 FRAUNHOFER AND FRESNEL DIFFRACTION IN ONE DIMENSION Revised November 15, 2017 INTRODUCTION The simplest and most commonly described examples of diffraction and interference from two-dimensional apertures
FRAUNHOFER AND FRESNEL DIFFRACTION IN ONE DIMENSION Revised November 15, 2017 INTRODUCTION The simplest and most commonly described examples of diffraction and interference from two-dimensional apertures
Using Optics to Optimize Your Machine Vision Application
 Expert Guide Using Optics to Optimize Your Machine Vision Application Introduction The lens is responsible for creating sufficient image quality to enable the vision system to extract the desired information
Expert Guide Using Optics to Optimize Your Machine Vision Application Introduction The lens is responsible for creating sufficient image quality to enable the vision system to extract the desired information
Integral 3-D Television Using a 2000-Scanning Line Video System
 Integral 3-D Television Using a 2000-Scanning Line Video System We have developed an integral three-dimensional (3-D) television that uses a 2000-scanning line video system. An integral 3-D television
Integral 3-D Television Using a 2000-Scanning Line Video System We have developed an integral three-dimensional (3-D) television that uses a 2000-scanning line video system. An integral 3-D television
Technical Note How to Compensate Lateral Chromatic Aberration
 Lateral Chromatic Aberration Compensation Function: In JAI color line scan cameras (3CCD/4CCD/3CMOS/4CMOS), sensors and prisms are precisely fabricated. On the other hand, the lens mounts of the cameras
Lateral Chromatic Aberration Compensation Function: In JAI color line scan cameras (3CCD/4CCD/3CMOS/4CMOS), sensors and prisms are precisely fabricated. On the other hand, the lens mounts of the cameras
ELEC Dr Reji Mathew Electrical Engineering UNSW
 ELEC 4622 Dr Reji Mathew Electrical Engineering UNSW Filter Design Circularly symmetric 2-D low-pass filter Pass-band radial frequency: ω p Stop-band radial frequency: ω s 1 δ p Pass-band tolerances: δ
ELEC 4622 Dr Reji Mathew Electrical Engineering UNSW Filter Design Circularly symmetric 2-D low-pass filter Pass-band radial frequency: ω p Stop-band radial frequency: ω s 1 δ p Pass-band tolerances: δ
Physics 2310 Lab #5: Thin Lenses and Concave Mirrors Dr. Michael Pierce (Univ. of Wyoming)
 Physics 2310 Lab #5: Thin Lenses and Concave Mirrors Dr. Michael Pierce (Univ. of Wyoming) Purpose: The purpose of this lab is to introduce students to some of the properties of thin lenses and mirrors.
Physics 2310 Lab #5: Thin Lenses and Concave Mirrors Dr. Michael Pierce (Univ. of Wyoming) Purpose: The purpose of this lab is to introduce students to some of the properties of thin lenses and mirrors.
(Refer Slide Time: 01:45)
 Digital Communication Professor Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Module 01 Lecture 21 Passband Modulations for Bandlimited Channels In our discussion
Digital Communication Professor Surendra Prasad Department of Electrical Engineering Indian Institute of Technology, Delhi Module 01 Lecture 21 Passband Modulations for Bandlimited Channels In our discussion
Photons and solid state detection
 Photons and solid state detection Photons represent discrete packets ( quanta ) of optical energy Energy is hc/! (h: Planck s constant, c: speed of light,! : wavelength) For solid state detection, photons
Photons and solid state detection Photons represent discrete packets ( quanta ) of optical energy Energy is hc/! (h: Planck s constant, c: speed of light,! : wavelength) For solid state detection, photons
Robert B.Hallock Draft revised April 11, 2006 finalpaper2.doc
 How to Optimize the Sharpness of Your Photographic Prints: Part II - Practical Limits to Sharpness in Photography and a Useful Chart to Deteremine the Optimal f-stop. Robert B.Hallock hallock@physics.umass.edu
How to Optimize the Sharpness of Your Photographic Prints: Part II - Practical Limits to Sharpness in Photography and a Useful Chart to Deteremine the Optimal f-stop. Robert B.Hallock hallock@physics.umass.edu
Compressive Through-focus Imaging
 PIERS ONLINE, VOL. 6, NO. 8, 788 Compressive Through-focus Imaging Oren Mangoubi and Edwin A. Marengo Yale University, USA Northeastern University, USA Abstract Optical sensing and imaging applications
PIERS ONLINE, VOL. 6, NO. 8, 788 Compressive Through-focus Imaging Oren Mangoubi and Edwin A. Marengo Yale University, USA Northeastern University, USA Abstract Optical sensing and imaging applications
A Study of Slanted-Edge MTF Stability and Repeatability
 A Study of Slanted-Edge MTF Stability and Repeatability Jackson K.M. Roland Imatest LLC, 2995 Wilderness Place Suite 103, Boulder, CO, USA ABSTRACT The slanted-edge method of measuring the spatial frequency
A Study of Slanted-Edge MTF Stability and Repeatability Jackson K.M. Roland Imatest LLC, 2995 Wilderness Place Suite 103, Boulder, CO, USA ABSTRACT The slanted-edge method of measuring the spatial frequency
APPLICATION NOTE
 THE PHYSICS BEHIND TAG OPTICS TECHNOLOGY AND THE MECHANISM OF ACTION OF APPLICATION NOTE 12-001 USING SOUND TO SHAPE LIGHT Page 1 of 6 Tutorial on How the TAG Lens Works This brief tutorial explains the
THE PHYSICS BEHIND TAG OPTICS TECHNOLOGY AND THE MECHANISM OF ACTION OF APPLICATION NOTE 12-001 USING SOUND TO SHAPE LIGHT Page 1 of 6 Tutorial on How the TAG Lens Works This brief tutorial explains the
IMAGE SENSOR SOLUTIONS. KAC-96-1/5" Lens Kit. KODAK KAC-96-1/5" Lens Kit. for use with the KODAK CMOS Image Sensors. November 2004 Revision 2
 KODAK for use with the KODAK CMOS Image Sensors November 2004 Revision 2 1.1 Introduction Choosing the right lens is a critical aspect of designing an imaging system. Typically the trade off between image
KODAK for use with the KODAK CMOS Image Sensors November 2004 Revision 2 1.1 Introduction Choosing the right lens is a critical aspect of designing an imaging system. Typically the trade off between image
On spatial resolution
 On spatial resolution Introduction How is spatial resolution defined? There are two main approaches in defining local spatial resolution. One method follows distinction criteria of pointlike objects (i.e.
On spatial resolution Introduction How is spatial resolution defined? There are two main approaches in defining local spatial resolution. One method follows distinction criteria of pointlike objects (i.e.
Math, Magic & MTF: A Cheat Sheet For The Vision System Community. By Stuart W. Singer, senior VP & CTO, and Jim Sullivan, director, Industrial Optics
 Math, Magic & MTF: A Cheat Sheet For The Vision System Community By Stuart W. Singer, senior VP & CTO, and Jim Sullivan, director, Industrial Optics The best indicator of lens performance what every buyer
Math, Magic & MTF: A Cheat Sheet For The Vision System Community By Stuart W. Singer, senior VP & CTO, and Jim Sullivan, director, Industrial Optics The best indicator of lens performance what every buyer
Image Formation. Light from distant things. Geometrical optics. Pinhole camera. Chapter 36
 Light from distant things Chapter 36 We learn about a distant thing from the light it generates or redirects. The lenses in our eyes create images of objects our brains can process. This chapter concerns
Light from distant things Chapter 36 We learn about a distant thing from the light it generates or redirects. The lenses in our eyes create images of objects our brains can process. This chapter concerns
Sharpness, Resolution and Interpolation
 Sharpness, Resolution and Interpolation Introduction There are a lot of misconceptions about resolution, camera pixel count, interpolation and their effect on astronomical images. Some of the confusion
Sharpness, Resolution and Interpolation Introduction There are a lot of misconceptions about resolution, camera pixel count, interpolation and their effect on astronomical images. Some of the confusion
ISO INTERNATIONAL STANDARD. Photography Electronic still-picture cameras Methods for measuring opto-electronic conversion functions (OECFs)
 INTERNATIONAL STANDARD ISO 14524 First edition 1999-12-15 Photography Electronic still-picture cameras Methods for measuring opto-electronic conversion functions (OECFs) Photographie Appareils de prises
INTERNATIONAL STANDARD ISO 14524 First edition 1999-12-15 Photography Electronic still-picture cameras Methods for measuring opto-electronic conversion functions (OECFs) Photographie Appareils de prises
Understanding Infrared Camera Thermal Image Quality
 Access to the world s leading infrared imaging technology Noise { Clean Signal www.sofradir-ec.com Understanding Infared Camera Infrared Inspection White Paper Abstract You ve no doubt purchased a digital
Access to the world s leading infrared imaging technology Noise { Clean Signal www.sofradir-ec.com Understanding Infared Camera Infrared Inspection White Paper Abstract You ve no doubt purchased a digital
Opto Engineering S.r.l.
 TUTORIAL #1 Telecentric Lenses: basic information and working principles On line dimensional control is one of the most challenging and difficult applications of vision systems. On the other hand, besides
TUTORIAL #1 Telecentric Lenses: basic information and working principles On line dimensional control is one of the most challenging and difficult applications of vision systems. On the other hand, besides
Resolution test with line patterns
 Resolution test with line patterns OBJECT IMAGE 1 line pair Resolution limit is usually given in line pairs per mm in sensor plane. Visual evaluation usually. Test of optics alone Magnifying glass Test
Resolution test with line patterns OBJECT IMAGE 1 line pair Resolution limit is usually given in line pairs per mm in sensor plane. Visual evaluation usually. Test of optics alone Magnifying glass Test
The popular conception of physics
 54 Teaching Physics: Inquiry and the Ray Model of Light Fernand Brunschwig, M.A.T. Program, Hudson Valley Center My thinking about these matters was stimulated by my participation on a panel devoted to
54 Teaching Physics: Inquiry and the Ray Model of Light Fernand Brunschwig, M.A.T. Program, Hudson Valley Center My thinking about these matters was stimulated by my participation on a panel devoted to
EC-433 Digital Image Processing
 EC-433 Digital Image Processing Lecture 2 Digital Image Fundamentals Dr. Arslan Shaukat 1 Fundamental Steps in DIP Image Acquisition An image is captured by a sensor (such as a monochrome or color TV camera)
EC-433 Digital Image Processing Lecture 2 Digital Image Fundamentals Dr. Arslan Shaukat 1 Fundamental Steps in DIP Image Acquisition An image is captured by a sensor (such as a monochrome or color TV camera)
Implementation of Adaptive Coded Aperture Imaging using a Digital Micro-Mirror Device for Defocus Deblurring
 Implementation of Adaptive Coded Aperture Imaging using a Digital Micro-Mirror Device for Defocus Deblurring Ashill Chiranjan and Bernardt Duvenhage Defence, Peace, Safety and Security Council for Scientific
Implementation of Adaptive Coded Aperture Imaging using a Digital Micro-Mirror Device for Defocus Deblurring Ashill Chiranjan and Bernardt Duvenhage Defence, Peace, Safety and Security Council for Scientific
Hello, welcome to the video lecture series on Digital Image Processing.
 Digital Image Processing. Professor P. K. Biswas. Department of Electronics and Electrical Communication Engineering. Indian Institute of Technology, Kharagpur. Lecture-33. Contrast Stretching Operation.
Digital Image Processing. Professor P. K. Biswas. Department of Electronics and Electrical Communication Engineering. Indian Institute of Technology, Kharagpur. Lecture-33. Contrast Stretching Operation.
Using Figures - The Basics
 Using Figures - The Basics by David Caprette, Rice University OVERVIEW To be useful, the results of a scientific investigation or technical project must be communicated to others in the form of an oral
Using Figures - The Basics by David Caprette, Rice University OVERVIEW To be useful, the results of a scientific investigation or technical project must be communicated to others in the form of an oral
10 GRAPHING LINEAR EQUATIONS
 0 GRAPHING LINEAR EQUATIONS We now expand our discussion of the single-variable equation to the linear equation in two variables, x and y. Some examples of linear equations are x+ y = 0, y = 3 x, x= 4,
0 GRAPHING LINEAR EQUATIONS We now expand our discussion of the single-variable equation to the linear equation in two variables, x and y. Some examples of linear equations are x+ y = 0, y = 3 x, x= 4,
Tech Paper. Anti-Sparkle Film Distinctness of Image Characterization
 Tech Paper Anti-Sparkle Film Distinctness of Image Characterization Anti-Sparkle Film Distinctness of Image Characterization Brian Hayden, Paul Weindorf Visteon Corporation, Michigan, USA Abstract: The
Tech Paper Anti-Sparkle Film Distinctness of Image Characterization Anti-Sparkle Film Distinctness of Image Characterization Brian Hayden, Paul Weindorf Visteon Corporation, Michigan, USA Abstract: The
Chapters 1 & 2. Definitions and applications Conceptual basis of photogrammetric processing
 Chapters 1 & 2 Chapter 1: Photogrammetry Definitions and applications Conceptual basis of photogrammetric processing Transition from two-dimensional imagery to three-dimensional information Automation
Chapters 1 & 2 Chapter 1: Photogrammetry Definitions and applications Conceptual basis of photogrammetric processing Transition from two-dimensional imagery to three-dimensional information Automation
Basic electronics Prof. T.S. Natarajan Department of Physics Indian Institute of Technology, Madras Lecture- 17. Frequency Analysis
 Basic electronics Prof. T.S. Natarajan Department of Physics Indian Institute of Technology, Madras Lecture- 17 Frequency Analysis Hello everybody! In our series of lectures on basic electronics learning
Basic electronics Prof. T.S. Natarajan Department of Physics Indian Institute of Technology, Madras Lecture- 17 Frequency Analysis Hello everybody! In our series of lectures on basic electronics learning
Criteria for Optical Systems: Optical Path Difference How do we determine the quality of a lens system? Several criteria used in optical design
 Criteria for Optical Systems: Optical Path Difference How do we determine the quality of a lens system? Several criteria used in optical design Computer Aided Design Several CAD tools use Ray Tracing (see
Criteria for Optical Systems: Optical Path Difference How do we determine the quality of a lens system? Several criteria used in optical design Computer Aided Design Several CAD tools use Ray Tracing (see
Combinational logic: Breadboard adders
 ! ENEE 245: Digital Circuits & Systems Lab Lab 1 Combinational logic: Breadboard adders ENEE 245: Digital Circuits and Systems Laboratory Lab 1 Objectives The objectives of this laboratory are the following:
! ENEE 245: Digital Circuits & Systems Lab Lab 1 Combinational logic: Breadboard adders ENEE 245: Digital Circuits and Systems Laboratory Lab 1 Objectives The objectives of this laboratory are the following:
Edge-Raggedness Evaluation Using Slanted-Edge Analysis
 Edge-Raggedness Evaluation Using Slanted-Edge Analysis Peter D. Burns Eastman Kodak Company, Rochester, NY USA 14650-1925 ABSTRACT The standard ISO 12233 method for the measurement of spatial frequency
Edge-Raggedness Evaluation Using Slanted-Edge Analysis Peter D. Burns Eastman Kodak Company, Rochester, NY USA 14650-1925 ABSTRACT The standard ISO 12233 method for the measurement of spatial frequency
In 1974, Erno Rubik created the Rubik s Cube. It is the most popular puzzle
 In 1974, Erno Rubik created the Rubik s Cube. It is the most popular puzzle worldwide. But now that it has been solved in 7.08 seconds, it seems that the world is in need of a new challenge. Melinda Green,
In 1974, Erno Rubik created the Rubik s Cube. It is the most popular puzzle worldwide. But now that it has been solved in 7.08 seconds, it seems that the world is in need of a new challenge. Melinda Green,
Lens Principal and Nodal Points
 Lens Principal and Nodal Points Douglas A. Kerr, P.E. Issue 3 January 21, 2004 ABSTRACT In discussions of photographic lenses, we often hear of the importance of the principal points and nodal points of
Lens Principal and Nodal Points Douglas A. Kerr, P.E. Issue 3 January 21, 2004 ABSTRACT In discussions of photographic lenses, we often hear of the importance of the principal points and nodal points of
Measurement of the Modulation Transfer Function (MTF) of a camera lens. Laboratoire d Enseignement Expérimental (LEnsE)
 Measurement of the Modulation Transfer Function (MTF) of a camera lens Aline Vernier, Baptiste Perrin, Thierry Avignon, Jean Augereau, Lionel Jacubowiez Institut d Optique Graduate School Laboratoire d
Measurement of the Modulation Transfer Function (MTF) of a camera lens Aline Vernier, Baptiste Perrin, Thierry Avignon, Jean Augereau, Lionel Jacubowiez Institut d Optique Graduate School Laboratoire d
Camera Resolution and Distortion: Advanced Edge Fitting
 28, Society for Imaging Science and Technology Camera Resolution and Distortion: Advanced Edge Fitting Peter D. Burns; Burns Digital Imaging and Don Williams; Image Science Associates Abstract A frequently
28, Society for Imaging Science and Technology Camera Resolution and Distortion: Advanced Edge Fitting Peter D. Burns; Burns Digital Imaging and Don Williams; Image Science Associates Abstract A frequently
Introduction to 2-D Copy Work
 Introduction to 2-D Copy Work What is the purpose of creating digital copies of your analogue work? To use for digital editing To submit work electronically to professors or clients To share your work
Introduction to 2-D Copy Work What is the purpose of creating digital copies of your analogue work? To use for digital editing To submit work electronically to professors or clients To share your work
Laboratory 1: Uncertainty Analysis
 University of Alabama Department of Physics and Astronomy PH101 / LeClair May 26, 2014 Laboratory 1: Uncertainty Analysis Hypothesis: A statistical analysis including both mean and standard deviation can
University of Alabama Department of Physics and Astronomy PH101 / LeClair May 26, 2014 Laboratory 1: Uncertainty Analysis Hypothesis: A statistical analysis including both mean and standard deviation can
Get the Shot! Photography + Instagram Workshop September 21, 2013 BlogPodium. Saturday, 21 September, 13
 Get the Shot! Photography + Instagram Workshop September 21, 2013 BlogPodium Part One: Taking your camera off manual Technical details Common problems and how to fix them Practice Ways to make your photos
Get the Shot! Photography + Instagram Workshop September 21, 2013 BlogPodium Part One: Taking your camera off manual Technical details Common problems and how to fix them Practice Ways to make your photos
Interference in stimuli employed to assess masking by substitution. Bernt Christian Skottun. Ullevaalsalleen 4C Oslo. Norway
 Interference in stimuli employed to assess masking by substitution Bernt Christian Skottun Ullevaalsalleen 4C 0852 Oslo Norway Short heading: Interference ABSTRACT Enns and Di Lollo (1997, Psychological
Interference in stimuli employed to assess masking by substitution Bernt Christian Skottun Ullevaalsalleen 4C 0852 Oslo Norway Short heading: Interference ABSTRACT Enns and Di Lollo (1997, Psychological
Digital Imaging Rochester Institute of Technology
 Digital Imaging 1999 Rochester Institute of Technology So Far... camera AgX film processing image AgX photographic film captures image formed by the optical elements (lens). Unfortunately, the processing
Digital Imaging 1999 Rochester Institute of Technology So Far... camera AgX film processing image AgX photographic film captures image formed by the optical elements (lens). Unfortunately, the processing
Single Slit Diffraction
 PC1142 Physics II Single Slit Diffraction 1 Objectives Investigate the single-slit diffraction pattern produced by monochromatic laser light. Determine the wavelength of the laser light from measurements
PC1142 Physics II Single Slit Diffraction 1 Objectives Investigate the single-slit diffraction pattern produced by monochromatic laser light. Determine the wavelength of the laser light from measurements
Fundamentals of Radio Interferometry
 Fundamentals of Radio Interferometry Rick Perley, NRAO/Socorro Fourteenth NRAO Synthesis Imaging Summer School Socorro, NM Topics Why Interferometry? The Single Dish as an interferometer The Basic Interferometer
Fundamentals of Radio Interferometry Rick Perley, NRAO/Socorro Fourteenth NRAO Synthesis Imaging Summer School Socorro, NM Topics Why Interferometry? The Single Dish as an interferometer The Basic Interferometer
Computer Generated Holograms for Testing Optical Elements
 Reprinted from APPLIED OPTICS, Vol. 10, page 619. March 1971 Copyright 1971 by the Optical Society of America and reprinted by permission of the copyright owner Computer Generated Holograms for Testing
Reprinted from APPLIED OPTICS, Vol. 10, page 619. March 1971 Copyright 1971 by the Optical Society of America and reprinted by permission of the copyright owner Computer Generated Holograms for Testing
REFLECTIONS AND STANDING WAVE RATIO
 Page 1 of 9 THE SMITH CHART.In the last section we looked at the properties of two particular lengths of resonant transmission lines: half and quarter wavelength lines. It is possible to compute the impedance
Page 1 of 9 THE SMITH CHART.In the last section we looked at the properties of two particular lengths of resonant transmission lines: half and quarter wavelength lines. It is possible to compute the impedance
EASTMAN EXR 200T Film / 5293, 7293
 TECHNICAL INFORMATION DATA SHEET Copyright, Eastman Kodak Company, 2003 1) Description EASTMAN EXR 200T Film / 5293 (35 mm), 7293 (16 mm) is a medium- to high-speed tungsten-balanced color negative camera
TECHNICAL INFORMATION DATA SHEET Copyright, Eastman Kodak Company, 2003 1) Description EASTMAN EXR 200T Film / 5293 (35 mm), 7293 (16 mm) is a medium- to high-speed tungsten-balanced color negative camera
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Mechanical Engineering Department. 2.71/2.710 Final Exam. May 21, Duration: 3 hours (9 am-12 noon)
 MASSACHUSETTS INSTITUTE OF TECHNOLOGY Mechanical Engineering Department 2.71/2.710 Final Exam May 21, 2013 Duration: 3 hours (9 am-12 noon) CLOSED BOOK Total pages: 5 Name: PLEASE RETURN THIS BOOKLET WITH
MASSACHUSETTS INSTITUTE OF TECHNOLOGY Mechanical Engineering Department 2.71/2.710 Final Exam May 21, 2013 Duration: 3 hours (9 am-12 noon) CLOSED BOOK Total pages: 5 Name: PLEASE RETURN THIS BOOKLET WITH
THE SINUSOIDAL WAVEFORM
 Chapter 11 THE SINUSOIDAL WAVEFORM The sinusoidal waveform or sine wave is the fundamental type of alternating current (ac) and alternating voltage. It is also referred to as a sinusoidal wave or, simply,
Chapter 11 THE SINUSOIDAL WAVEFORM The sinusoidal waveform or sine wave is the fundamental type of alternating current (ac) and alternating voltage. It is also referred to as a sinusoidal wave or, simply,
Format Size in Digital Photography
 Format Size in Digital Photography Douglas A. Kerr, P.E. Issue 2 September 8, 2005 ABSTRACT In photography, the term format size describes the actual physical size of the image captured by the film frame,
Format Size in Digital Photography Douglas A. Kerr, P.E. Issue 2 September 8, 2005 ABSTRACT In photography, the term format size describes the actual physical size of the image captured by the film frame,
Exercise 1-3. Radar Antennas EXERCISE OBJECTIVE DISCUSSION OUTLINE DISCUSSION OF FUNDAMENTALS. Antenna types
 Exercise 1-3 Radar Antennas EXERCISE OBJECTIVE When you have completed this exercise, you will be familiar with the role of the antenna in a radar system. You will also be familiar with the intrinsic characteristics
Exercise 1-3 Radar Antennas EXERCISE OBJECTIVE When you have completed this exercise, you will be familiar with the role of the antenna in a radar system. You will also be familiar with the intrinsic characteristics
Module 1: Introduction to Experimental Techniques Lecture 2: Sources of error. The Lecture Contains: Sources of Error in Measurement
 The Lecture Contains: Sources of Error in Measurement Signal-To-Noise Ratio Analog-to-Digital Conversion of Measurement Data A/D Conversion Digitalization Errors due to A/D Conversion file:///g /optical_measurement/lecture2/2_1.htm[5/7/2012
The Lecture Contains: Sources of Error in Measurement Signal-To-Noise Ratio Analog-to-Digital Conversion of Measurement Data A/D Conversion Digitalization Errors due to A/D Conversion file:///g /optical_measurement/lecture2/2_1.htm[5/7/2012
ISO INTERNATIONAL STANDARD. Photography Electronic still-picture cameras Methods for measuring optoelectronic conversion functions (OECFs)
 INTERNATIONAL STANDARD ISO 14524 Second edition 2009-02-15 Photography Electronic still-picture cameras Methods for measuring optoelectronic conversion functions (OECFs) Photographie Appareils de prises
INTERNATIONAL STANDARD ISO 14524 Second edition 2009-02-15 Photography Electronic still-picture cameras Methods for measuring optoelectronic conversion functions (OECFs) Photographie Appareils de prises
Diffraction. Interference with more than 2 beams. Diffraction gratings. Diffraction by an aperture. Diffraction of a laser beam
 Diffraction Interference with more than 2 beams 3, 4, 5 beams Large number of beams Diffraction gratings Equation Uses Diffraction by an aperture Huygen s principle again, Fresnel zones, Arago s spot Qualitative
Diffraction Interference with more than 2 beams 3, 4, 5 beams Large number of beams Diffraction gratings Equation Uses Diffraction by an aperture Huygen s principle again, Fresnel zones, Arago s spot Qualitative
Charged Coupled Device (CCD) S.Vidhya
 Charged Coupled Device (CCD) S.Vidhya 02.04.2016 Sensor Physical phenomenon Sensor Measurement Output A sensor is a device that measures a physical quantity and converts it into a signal which can be read
Charged Coupled Device (CCD) S.Vidhya 02.04.2016 Sensor Physical phenomenon Sensor Measurement Output A sensor is a device that measures a physical quantity and converts it into a signal which can be read
SECTION I - CHAPTER 2 DIGITAL IMAGING PROCESSING CONCEPTS
 RADT 3463 - COMPUTERIZED IMAGING Section I: Chapter 2 RADT 3463 Computerized Imaging 1 SECTION I - CHAPTER 2 DIGITAL IMAGING PROCESSING CONCEPTS RADT 3463 COMPUTERIZED IMAGING Section I: Chapter 2 RADT
RADT 3463 - COMPUTERIZED IMAGING Section I: Chapter 2 RADT 3463 Computerized Imaging 1 SECTION I - CHAPTER 2 DIGITAL IMAGING PROCESSING CONCEPTS RADT 3463 COMPUTERIZED IMAGING Section I: Chapter 2 RADT
TSBB09 Image Sensors 2018-HT2. Image Formation Part 1
 TSBB09 Image Sensors 2018-HT2 Image Formation Part 1 Basic physics Electromagnetic radiation consists of electromagnetic waves With energy That propagate through space The waves consist of transversal
TSBB09 Image Sensors 2018-HT2 Image Formation Part 1 Basic physics Electromagnetic radiation consists of electromagnetic waves With energy That propagate through space The waves consist of transversal
Thermography. White Paper: Understanding Infrared Camera Thermal Image Quality
 Electrophysics Resource Center: White Paper: Understanding Infrared Camera 373E Route 46, Fairfield, NJ 07004 Phone: 973-882-0211 Fax: 973-882-0997 www.electrophysics.com Understanding Infared Camera Electrophysics
Electrophysics Resource Center: White Paper: Understanding Infrared Camera 373E Route 46, Fairfield, NJ 07004 Phone: 973-882-0211 Fax: 973-882-0997 www.electrophysics.com Understanding Infared Camera Electrophysics
Chapter 2 Fourier Integral Representation of an Optical Image
 Chapter 2 Fourier Integral Representation of an Optical This chapter describes optical transfer functions. The concepts of linearity and shift invariance were introduced in Chapter 1. This chapter continues
Chapter 2 Fourier Integral Representation of an Optical This chapter describes optical transfer functions. The concepts of linearity and shift invariance were introduced in Chapter 1. This chapter continues
Exercise questions for Machine vision
 Exercise questions for Machine vision This is a collection of exercise questions. These questions are all examination alike which means that similar questions may appear at the written exam. I ve divided
Exercise questions for Machine vision This is a collection of exercise questions. These questions are all examination alike which means that similar questions may appear at the written exam. I ve divided
Chapter 3 Data and Signals 3.1
 Chapter 3 Data and Signals 3.1 Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Note To be transmitted, data must be transformed to electromagnetic signals. 3.2
Chapter 3 Data and Signals 3.1 Copyright The McGraw-Hill Companies, Inc. Permission required for reproduction or display. Note To be transmitted, data must be transformed to electromagnetic signals. 3.2
Optical design of a high resolution vision lens
 Optical design of a high resolution vision lens Paul Claassen, optical designer, paul.claassen@sioux.eu Marnix Tas, optical specialist, marnix.tas@sioux.eu Prof L.Beckmann, l.beckmann@hccnet.nl Summary:
Optical design of a high resolution vision lens Paul Claassen, optical designer, paul.claassen@sioux.eu Marnix Tas, optical specialist, marnix.tas@sioux.eu Prof L.Beckmann, l.beckmann@hccnet.nl Summary:
DSP First Lab 06: Digital Images: A/D and D/A
 DSP First Lab 06: Digital Images: A/D and D/A Pre-Lab and Warm-Up: You should read at least the Pre-Lab and Warm-up sections of this lab assignment and go over all exercises in the Pre-Lab section before
DSP First Lab 06: Digital Images: A/D and D/A Pre-Lab and Warm-Up: You should read at least the Pre-Lab and Warm-up sections of this lab assignment and go over all exercises in the Pre-Lab section before
Modeling and Synthesis of Aperture Effects in Cameras
 Modeling and Synthesis of Aperture Effects in Cameras Douglas Lanman, Ramesh Raskar, and Gabriel Taubin Computational Aesthetics 2008 20 June, 2008 1 Outline Introduction and Related Work Modeling Vignetting
Modeling and Synthesis of Aperture Effects in Cameras Douglas Lanman, Ramesh Raskar, and Gabriel Taubin Computational Aesthetics 2008 20 June, 2008 1 Outline Introduction and Related Work Modeling Vignetting
Why learn about photography in this course?
 Why learn about photography in this course? Geri's Game: Note the background is blurred. - photography: model of image formation - Many computer graphics methods use existing photographs e.g. texture &
Why learn about photography in this course? Geri's Game: Note the background is blurred. - photography: model of image formation - Many computer graphics methods use existing photographs e.g. texture &
Zone. ystem. Handbook. Part 2 The Zone System in Practice. by Jeff Curto
 A Zone S ystem Handbook Part 2 The Zone System in Practice by This handout was produced in support of s Camera Position Podcast. Reproduction and redistribution of this document is fine, so long as the
A Zone S ystem Handbook Part 2 The Zone System in Practice by This handout was produced in support of s Camera Position Podcast. Reproduction and redistribution of this document is fine, so long as the
CSE 473/573 Computer Vision and Image Processing (CVIP)
 CSE 473/573 Computer Vision and Image Processing (CVIP) Ifeoma Nwogu inwogu@buffalo.edu Lecture 4 Image formation(part I) Schedule Last class linear algebra overview Today Image formation and camera properties
CSE 473/573 Computer Vision and Image Processing (CVIP) Ifeoma Nwogu inwogu@buffalo.edu Lecture 4 Image formation(part I) Schedule Last class linear algebra overview Today Image formation and camera properties
(Refer Slide Time: 3:11)
 Digital Communication. Professor Surendra Prasad. Department of Electrical Engineering. Indian Institute of Technology, Delhi. Lecture-2. Digital Representation of Analog Signals: Delta Modulation. Professor:
Digital Communication. Professor Surendra Prasad. Department of Electrical Engineering. Indian Institute of Technology, Delhi. Lecture-2. Digital Representation of Analog Signals: Delta Modulation. Professor:
Norwood s dome: a revolution in incident-light photographic exposure metering
 Norwood s dome: a revolution in incident-light photographic exposure metering Douglas A. Kerr Issue 2 October 14, 2016 ABSTRACT AND INTRODUCTION In the late 1930 s, Donald W. Norwood introduced a new principle
Norwood s dome: a revolution in incident-light photographic exposure metering Douglas A. Kerr Issue 2 October 14, 2016 ABSTRACT AND INTRODUCTION In the late 1930 s, Donald W. Norwood introduced a new principle
OPTICS I LENSES AND IMAGES
 APAS Laboratory Optics I OPTICS I LENSES AND IMAGES If at first you don t succeed try, try again. Then give up- there s no sense in being foolish about it. -W.C. Fields SYNOPSIS: In Optics I you will learn
APAS Laboratory Optics I OPTICS I LENSES AND IMAGES If at first you don t succeed try, try again. Then give up- there s no sense in being foolish about it. -W.C. Fields SYNOPSIS: In Optics I you will learn
lecture 24 image capture - photography: model of image formation - image blur - camera settings (f-number, shutter speed) - exposure - camera response
 lecture 24 image capture - photography: model of image formation - image blur - camera settings (f-number, shutter speed) - exposure - camera response - application: high dynamic range imaging Why learn
lecture 24 image capture - photography: model of image formation - image blur - camera settings (f-number, shutter speed) - exposure - camera response - application: high dynamic range imaging Why learn
This document is a preview generated by EVS
 INTERNATIONAL STANDARD ISO 17850 First edition 2015-07-01 Photography Digital cameras Geometric distortion (GD) measurements Photographie Caméras numériques Mesurages de distorsion géométrique (DG) Reference
INTERNATIONAL STANDARD ISO 17850 First edition 2015-07-01 Photography Digital cameras Geometric distortion (GD) measurements Photographie Caméras numériques Mesurages de distorsion géométrique (DG) Reference
A Beginner s Guide To Exposure
 A Beginner s Guide To Exposure What is exposure? A Beginner s Guide to Exposure What is exposure? According to Wikipedia: In photography, exposure is the amount of light per unit area (the image plane
A Beginner s Guide To Exposure What is exposure? A Beginner s Guide to Exposure What is exposure? According to Wikipedia: In photography, exposure is the amount of light per unit area (the image plane
An Evaluation of MTF Determination Methods for 35mm Film Scanners
 An Evaluation of Determination Methods for 35mm Film Scanners S. Triantaphillidou, R. E. Jacobson, R. Fagard-Jenkin Imaging Technology Research Group, University of Westminster Watford Road, Harrow, HA1
An Evaluation of Determination Methods for 35mm Film Scanners S. Triantaphillidou, R. E. Jacobson, R. Fagard-Jenkin Imaging Technology Research Group, University of Westminster Watford Road, Harrow, HA1
Introduction to DSP ECE-S352 Fall Quarter 2000 Matlab Project 1
 Objective: Introduction to DSP ECE-S352 Fall Quarter 2000 Matlab Project 1 This Matlab Project is an extension of the basic correlation theory presented in the course. It shows a practical application
Objective: Introduction to DSP ECE-S352 Fall Quarter 2000 Matlab Project 1 This Matlab Project is an extension of the basic correlation theory presented in the course. It shows a practical application
Designing Information Devices and Systems I Spring 2019 Lecture Notes Note Introduction to Electrical Circuit Analysis
 EECS 16A Designing Information Devices and Systems I Spring 2019 Lecture Notes Note 11 11.1 Introduction to Electrical Circuit Analysis Our ultimate goal is to design systems that solve people s problems.
EECS 16A Designing Information Devices and Systems I Spring 2019 Lecture Notes Note 11 11.1 Introduction to Electrical Circuit Analysis Our ultimate goal is to design systems that solve people s problems.
