b = and their properties: b 1 b 2 b 3 a b is perpendicular to both a and 1 b = x = x 0 + at y = y 0 + bt z = z 0 + ct ; y = y 0 )
|
|
|
- Ami Hancock
- 5 years ago
- Views:
Transcription
1 ***************** Disclimer ***************** This represents very brief outline of most of the topics covered MA261 *************************************************** I. Vectors, Lines nd Plnes 1. Vector rithmetic; directed vector P 0 P 1 from P 0 to P 1 ; dot product of vectors ( 1 i+2 j+3 k) (b1 i+b2 j+b3 k)=1 b b b 3 ; ngle between two vectors, b cos θ = b ; cross product i j k b = nd their properties: b 1 b 2 b 3 b is perpendiculr to both nd 1 b, 2 b = re of tringle spnned by nd b; projections pr b = b ; v = v (cos θ i +sinθ j) Eqution of line contining (x 0,y 0,z 0 ), direction vector L = i + b j + c k: () Vector Form: r = r 0 + t L, (b) Prmetric Form: x = x 0 + t y = y 0 + bt z = z 0 + ct x x 0 (c) Symmetric Form: = y y 0 = z z 0 b c (if sy b = 0, then x x 0 = z z 0 c ; y = y 0 ) where r 0 = x 0 i + y0 j + z0 k 3. Eqution of plne contining (x 0,y 0,z 0 ), norml vector N = i + b j + c k: N P 0 P =0 or (x x 0 )+b(y y 0 )+c(z z 0 )=0. 4. Sketching plnes (look t intercepts : x + y b + z c = 1). II. Vector-Vlued Functions 1. Differentiting nd integrting vector-vlued functions nd sketching the corresponding curves. 2. Prmeterizing curves of the form sy y = f(x), x b ( : r(t) =t i + f(t) j, t b). 3. Unit tngent vector T(t) = r (t) r (t) ; length of curve b r (t) dt.
2 III. Prtil Derivtives 1. Domins of functions of severl vribles; level curves f(x, y) =, level surfces f(x, y, z) =; sketching surfces using level curves. 2. Qudric surfces. 3. omputing limits, determining when limits exist. 4. Prtil derivtives; HAIN RULE (consider tree digrms). 5. Implicit Differentition, for exmple : () If y = y(x) is defined implicitly by F (x, y) = 0, then (b) If z = z(x, y) is defined implicitly by F (x, y, z) = 0, then dy dx = x x = x nd =. 6. Grdients: f(x, y, z) =f x i + fy j + fz k; the grdient f(x, y) is perpendiculr to level curve f(x, y) = nd f(x, y, z) is perpendiculr to level surfce f(x, y, z) =. 7. Directionl derivtive : D u f(x, y, z) = f(x, y, z) u, where u is UNIT vector; f D u f f ; f(x, y, z) increses fstest in the direction f. 8. Norml vector n to surfces : () is level surfce, F (x, y, z) =, then norml is n = F (x, y, z). (b) is the grph of z = f(x, y), then norml is n = f x i fy j + k 9. Tngent plnes to surfces; Tngent Plne Approximtion Formul: f(x + h, y + k) f(x, y)+f x (x, y) h + f y (x, y) k. 10. riticl points of f(x, y, z) : points where f(x, y, z) = 0 or f(x, y, z) does not exist.
3 11. Finding reltive extrem of f(x, y) t those prticulr criticl points (x 0,y 0 ) where f(x 0,y 0 )= 0 using 2 nd Prtils Test: let D(x, y) = f xx f xy () If D(x 0,y 0 ) > 0ndf xx (x 0,y 0 ) > 0 f hs rel minimum vlue t (x 0,y 0 ) (b) If D(x 0,y 0 ) > 0ndf xx (x 0,y 0 ) < 0 f hs rel mximum vlue t (x 0,y 0 ) (c) If D(x 0,y 0 ) < 0 f hs sddle point t (x 0,y 0 ). 12. Finding bsolute extrem over closed, bounded regions: find interior criticl points, find points on the boundry where extrem my occur, mke tble of vlues of f t ll these points. 13. onstrined extreml problems: Mximize nd/orminimize f(x, y) subject f = λ g to the condition g(x, y) =; Lgrnge Multipliers: g(x, y) = IV. Multiple Integrls 1. Double integrls; verticlly nd horizontlly simple regions, iterted integrls; double integrls in polr coordintes (da = rdrdθ) 2. Applictions of double integrls: res between curves, volumes, surfce re S = fx 2 + f y 2 +1dA. R 3. hnging the order of integrtion in double integrls. 4. Triple integrls; iterted triple integrls; pplictions of triple integrls: volumes, mss m = δ(x, y, z) dv. D 5. Triple integrls in Rectngulr, ylindricl, nd Sphericl oordintes: () Rectngulr oordintes: dv = dz dy dx or dv = dz dx dy, etc (b) (c) ylindricl oordintes: Sphericl oordintes: x = r cos θ y = r sin θ z = z x = ρ sin φ cos θ y = ρ sin φ sin θ z = ρ cos φ dv = rdzdrdθ f xy f yy dv = ρ 2 sin φdρdφdθ
4 V. Vector Fields 1. Vector fields F = M i + N j + P k ; divergence nd curl of vector field F: div F = F = M x + N y + P z curl F = F = i j k x M N P ; Lplcin of f =div f = 2 f = f xx + f yy + f zz. 2. onservtive vector fields F = f; how to determine if F is conservtive : check tht curl F = 0 (if region hs no holes ); given tht F = f, know how to determine the potentil function f(x, y, z). 3. Line integrls of functions f(x, y, z) ds = b f(x(t),y(t),z(t)) r (t) dt; line integrls of vector fields F = M i + N j + P k : F dr = b F( r(t)) r (t) dt or equivlently Mdx+ Ndy+ Pdz= b Mx dt + Ny dt + Pz dt, where : r(t) =x(t) i + y(t) j + z(t) k, t b. 4. Fundmentl Theorem of Line Integrls: f dr = f(p 1 ) f(p 0 ); independence of pth (check if F = f or curl F = 0) ; pplictions to work W = F dr. 5. Green s Theorem :If is closed curve trversed counterclockwise, then M(x, y) dx + N(x, y) dy = R ( N x M ) 6. Surfce integrls : if is the grph of z = f(x, y) with (x, y) R, then g(x, y, z) ds = R g(x, y, f(x, y)) fx 2 + f y 2 +1 da. da.
5 7. Flux integrl of F = M i+n j+p k over the surfce, the grph of z = f(x, y) with (x, y) R, nd n = upper unit norml vector to : F n ds = R { M f x Nf y + P } da. 8. Divergence Theorem (Guss Theorem) : If D is solid region nd is its closed boundry surfce, n = outer unit norml to, then F n ds = D div F dv.
Study Guide # Vectors in R 2 and R 3. (a) v = a, b, c = a i + b j + c k; vector addition and subtraction geometrically using parallelograms
 Study Guide # 1 MA 26100 - Fll 2018 1. Vectors in R 2 nd R 3 () v =, b, c = i + b j + c k; vector ddition nd subtrction geometriclly using prllelogrms spnned by u nd v; length or mgnitude of v =, b, c,
Study Guide # 1 MA 26100 - Fll 2018 1. Vectors in R 2 nd R 3 () v =, b, c = i + b j + c k; vector ddition nd subtrction geometriclly using prllelogrms spnned by u nd v; length or mgnitude of v =, b, c,
STUDY GUIDE, CALCULUS III, 2017 SPRING
 TUY GUIE, ALULU III, 2017 PING ontents hpter 13. Functions of severl vribles 1 13.1. Plnes nd surfces 2 13.2. Grphs nd level curves 2 13.3. Limit of function of two vribles 2 13.4. Prtil derivtives 2 13.5.
TUY GUIE, ALULU III, 2017 PING ontents hpter 13. Functions of severl vribles 1 13.1. Plnes nd surfces 2 13.2. Grphs nd level curves 2 13.3. Limit of function of two vribles 2 13.4. Prtil derivtives 2 13.5.
Chapter 12 Vectors and the Geometry of Space 12.1 Three-dimensional Coordinate systems
 hpter 12 Vectors nd the Geometry of Spce 12.1 Three-dimensionl oordinte systems A. Three dimensionl Rectngulr oordinte Sydstem: The rtesin product where (x, y, z) isclled ordered triple. B. istnce: R 3
hpter 12 Vectors nd the Geometry of Spce 12.1 Three-dimensionl oordinte systems A. Three dimensionl Rectngulr oordinte Sydstem: The rtesin product where (x, y, z) isclled ordered triple. B. istnce: R 3
WI1402-LR Calculus II Delft University of Technology
 WI402-LR lculus II elft University of Technology Yer 203 204 Michele Fcchinelli Version.0 Lst modified on Februry, 207 Prefce This summry ws written for the course WI402-LR lculus II, tught t the elft
WI402-LR lculus II elft University of Technology Yer 203 204 Michele Fcchinelli Version.0 Lst modified on Februry, 207 Prefce This summry ws written for the course WI402-LR lculus II, tught t the elft
Vector Calculus. 1 Line Integrals
 Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Vector lculus 1 Line Integrls Mss problem. Find the mss M of very thin wire whose liner density function (the mss per unit length) is known. We model the wire by smooth curve between two points P nd Q
Example. Check that the Jacobian of the transformation to spherical coordinates is
 lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
lss, given on Feb 3, 2, for Mth 3, Winter 2 Recll tht the fctor which ppers in chnge of vrible formul when integrting is the Jcobin, which is the determinnt of mtrix of first order prtil derivtives. Exmple.
Lecture 20. Intro to line integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Lecture 2 Intro to line integrls Dn Nichols nichols@mth.umss.edu MATH 233, Spring 218 University of Msschusetts April 12, 218 (2) onservtive vector fields We wnt to determine if F P (x, y), Q(x, y) is
Polar Coordinates. July 30, 2014
 Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Polr Coordintes July 3, 4 Sometimes it is more helpful to look t point in the xy-plne not in terms of how fr it is horizontlly nd verticlly (this would men looking t the Crtesin, or rectngulr, coordintes
Math 116 Calculus II
 Mth 6 Clculus II Contents 7 Additionl topics in Integrtion 7. Integrtion by prts..................................... 7.4 Numericl Integrtion.................................... 7 7.5 Improper Integrl......................................
Mth 6 Clculus II Contents 7 Additionl topics in Integrtion 7. Integrtion by prts..................................... 7.4 Numericl Integrtion.................................... 7 7.5 Improper Integrl......................................
Section 17.2: Line Integrals. 1 Objectives. 2 Assignments. 3 Maple Commands. 1. Compute line integrals in IR 2 and IR Read Section 17.
 Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
Section 7.: Line Integrls Objectives. ompute line integrls in IR nd IR 3. Assignments. Red Section 7.. Problems:,5,9,,3,7,,4 3. hllenge: 6,3,37 4. Red Section 7.3 3 Mple ommnds Mple cn ctully evlute line
13.1 Double Integral over Rectangle. f(x ij,y ij ) i j I <ɛ. f(x, y)da.
 CHAPTE 3, MULTIPLE INTEGALS Definition. 3. Double Integrl over ectngle A function f(x, y) is integrble on rectngle [, b] [c, d] if there is number I such tht for ny given ɛ>0thereisδ>0 such tht, fir ny
CHAPTE 3, MULTIPLE INTEGALS Definition. 3. Double Integrl over ectngle A function f(x, y) is integrble on rectngle [, b] [c, d] if there is number I such tht for ny given ɛ>0thereisδ>0 such tht, fir ny
VectorPlot[{y^2-2x*y,3x*y-6*x^2},{x,-5,5},{y,-5,5}]
![VectorPlot[{y^2-2x*y,3x*y-6*x^2},{x,-5,5},{y,-5,5}] VectorPlot[{y^2-2x*y,3x*y-6*x^2},{x,-5,5},{y,-5,5}]](/thumbs/88/116610289.jpg) hapter 16 16.1. 6. Notice that F(x, y) has length 1 and that it is perpendicular to the position vector (x, y) for all x and y (except at the origin). Think about drawing the vectors based on concentric
hapter 16 16.1. 6. Notice that F(x, y) has length 1 and that it is perpendicular to the position vector (x, y) for all x and y (except at the origin). Think about drawing the vectors based on concentric
Lecture 16. Double integrals. Dan Nichols MATH 233, Spring 2018 University of Massachusetts.
 Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Leture 16 Double integrls Dn Nihols nihols@mth.umss.edu MATH 233, Spring 218 University of Msshusetts Mrh 27, 218 (2) iemnn sums for funtions of one vrible Let f(x) on [, b]. We n estimte the re under
Double Integrals over Rectangles
 Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of
Jim Lmbers MAT 8 Spring Semester 9- Leture Notes These notes orrespond to Setion. in Stewrt nd Setion 5. in Mrsden nd Tromb. Double Integrls over etngles In single-vrible lulus, the definite integrl of
Test Yourself. 11. The angle in degrees between u and w. 12. A vector parallel to v, but of length 2.
 Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
Test Yourself These are problems you might see in a vector calculus course. They are general questions and are meant for practice. The key follows, but only with the answers. an you fill in the blanks
VECTOR CALCULUS Julian.O 2016
 VETO ALULUS Julian.O 2016 Vector alculus Lecture 3: Double Integrals Green s Theorem Divergence of a Vector Field Double Integrals: Double integrals are used to integrate two-variable functions f(x, y)
VETO ALULUS Julian.O 2016 Vector alculus Lecture 3: Double Integrals Green s Theorem Divergence of a Vector Field Double Integrals: Double integrals are used to integrate two-variable functions f(x, y)
CHAPTER 11 PARTIAL DERIVATIVES
 CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
CHAPTER 11 PARTIAL DERIVATIVES 1. FUNCTIONS OF SEVERAL VARIABLES A) Definition: A function of two variables is a rule that assigns to each ordered pair of real numbers (x,y) in a set D a unique real number
10.4 AREAS AND LENGTHS IN POLAR COORDINATES
 65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
65 CHAPTER PARAMETRIC EQUATINS AND PLAR CRDINATES.4 AREAS AND LENGTHS IN PLAR CRDINATES In this section we develop the formul for the re of region whose oundry is given y polr eqution. We need to use the
Differentiable functions (Sec. 14.4)
 Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Math 20C Multivariable Calculus Lecture 3 Differentiable functions (Sec. 4.4) Review: Partial derivatives. Slide Partial derivatives and continuity. Equation of the tangent plane. Differentiable functions.
Section 16.3 Double Integrals over General Regions
 Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
Section 6.3 Double Integrls over Generl egions Not ever region is rectngle In the lst two sections we considered the problem of integrting function of two vribles over rectngle. This sitution however is
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION
 FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
FUNCTIONS OF SEVERAL VARIABLES AND PARTIAL DIFFERENTIATION 1. Functions of Several Variables A function of two variables is a rule that assigns a real number f(x, y) to each ordered pair of real numbers
Geometric quantities for polar curves
 Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
Roerto s Notes on Integrl Clculus Chpter 5: Bsic pplictions of integrtion Section 10 Geometric quntities for polr curves Wht you need to know lredy: How to use integrls to compute res nd lengths of regions
9.4. ; 65. A family of curves has polar equations. ; 66. The astronomer Giovanni Cassini ( ) studied the family of curves with polar equations
 54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
54 CHAPTER 9 PARAMETRIC EQUATINS AND PLAR CRDINATES 49. r, 5. r sin 3, 5 54 Find the points on the given curve where the tngent line is horizontl or verticl. 5. r 3 cos 5. r e 53. r cos 54. r sin 55. Show
Exam 2 Review Sheet. r(t) = x(t), y(t), z(t)
 Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Exam 2 Review Sheet Joseph Breen Particle Motion Recall that a parametric curve given by: r(t) = x(t), y(t), z(t) can be interpreted as the position of a particle. Then the derivative represents the particle
Triangles and parallelograms of equal area in an ellipse
 1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
1 Tringles nd prllelogrms of equl re in n ellipse Roert Buonpstore nd Thoms J Osler Mthemtics Deprtment RownUniversity Glssoro, NJ 0808 USA uonp0@studentsrownedu osler@rownedu Introduction In the pper
[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and
![[f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and [f(t)] 2 + [g(t)] 2 + [h(t)] 2 dt. [f(u)] 2 + [g(u)] 2 + [h(u)] 2 du. The Fundamental Theorem of Calculus implies that s(t) is differentiable and](/thumbs/92/108353356.jpg) Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
Midterm 2 review Math 265 Fall 2007 13.3. Arc Length and Curvature. Assume that the curve C is described by the vector-valued function r(r) = f(t), g(t), h(t), and that C is traversed exactly once as t
2.1 Partial Derivatives
 .1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
.1 Partial Derivatives.1.1 Functions of several variables Up until now, we have only met functions of single variables. From now on we will meet functions such as z = f(x, y) and w = f(x, y, z), which
Definitions and claims functions of several variables
 Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Definitions and claims functions of several variables In the Euclidian space I n of all real n-dimensional vectors x = (x 1, x,..., x n ) the following are defined: x + y = (x 1 + y 1, x + y,..., x n +
Independence of Path and Conservative Vector Fields
 Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Independence of Path and onservative Vector Fields MATH 311, alculus III J. Robert Buchanan Department of Mathematics Summer 2011 Goal We would like to know conditions on a vector field function F(x, y)
Independent of path Green s Theorem Surface Integrals. MATH203 Calculus. Dr. Bandar Al-Mohsin. School of Mathematics, KSU 20/4/14
 School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
School of Mathematics, KSU 20/4/14 Independent of path Theorem 1 If F (x, y) = M(x, y)i + N(x, y)j is continuous on an open connected region D, then the line integral F dr is independent of path if and
ANSWER KEY. (a) For each of the following partials derivatives, use the contour plot to decide whether they are positive, negative, or zero.
 Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
Math 2130-101 Test #2 for Section 101 October 14 th, 2009 ANSWE KEY 1. (10 points) Compute the curvature of r(t) = (t + 2, 3t + 4, 5t + 6). r (t) = (1, 3, 5) r (t) = 1 2 + 3 2 + 5 2 = 35 T(t) = 1 r (t)
Review guide for midterm 2 in Math 233 March 30, 2009
 Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
Review guide for midterm 2 in Math 2 March, 29 Midterm 2 covers material that begins approximately with the definition of partial derivatives in Chapter 4. and ends approximately with methods for calculating
WESI 205 Workbook. 1 Review. 2 Graphing in 3D
 1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
1 Review 1. (a) Use a right triangle to compute the distance between (x 1, y 1 ) and (x 2, y 2 ) in R 2. (b) Use this formula to compute the equation of a circle centered at (a, b) with radius r. (c) Extend
47. Conservative Vector Fields
 47. onservative Vector Fields Given a function z = φ(x, y), its gradient is φ = φ x, φ y. Thus, φ is a gradient (or conservative) vector field, and the function φ is called a potential function. Suppose
47. onservative Vector Fields Given a function z = φ(x, y), its gradient is φ = φ x, φ y. Thus, φ is a gradient (or conservative) vector field, and the function φ is called a potential function. Suppose
Math Final Exam - 6/11/2015
 Math 200 - Final Exam - 6/11/2015 Name: Section: Section Class/Times Instructor Section Class/Times Instructor 1 9:00%AM ( 9:50%AM Papadopoulos,%Dimitrios 11 1:00%PM ( 1:50%PM Swartz,%Kenneth 2 11:00%AM
Math 200 - Final Exam - 6/11/2015 Name: Section: Section Class/Times Instructor Section Class/Times Instructor 1 9:00%AM ( 9:50%AM Papadopoulos,%Dimitrios 11 1:00%PM ( 1:50%PM Swartz,%Kenneth 2 11:00%AM
1. Vector Fields. f 1 (x, y, z)i + f 2 (x, y, z)j + f 3 (x, y, z)k.
 HAPTER 14 Vector alculus 1. Vector Fields Definition. A vector field in the plane is a function F(x, y) from R into V, We write F(x, y) = hf 1 (x, y), f (x, y)i = f 1 (x, y)i + f (x, y)j. A vector field
HAPTER 14 Vector alculus 1. Vector Fields Definition. A vector field in the plane is a function F(x, y) from R into V, We write F(x, y) = hf 1 (x, y), f (x, y)i = f 1 (x, y)i + f (x, y)j. A vector field
University of California, Berkeley Department of Mathematics 5 th November, 2012, 12:10-12:55 pm MATH 53 - Test #2
 University of California, Berkeley epartment of Mathematics 5 th November, 212, 12:1-12:55 pm MATH 53 - Test #2 Last Name: First Name: Student Number: iscussion Section: Name of GSI: Record your answers
University of California, Berkeley epartment of Mathematics 5 th November, 212, 12:1-12:55 pm MATH 53 - Test #2 Last Name: First Name: Student Number: iscussion Section: Name of GSI: Record your answers
Mock final exam Math fall 2007
 Mock final exam Math - fall 7 Fernando Guevara Vasquez December 5 7. Consider the curve r(t) = ti + tj + 5 t t k, t. (a) Show that the curve lies on a sphere centered at the origin. (b) Where does the
Mock final exam Math - fall 7 Fernando Guevara Vasquez December 5 7. Consider the curve r(t) = ti + tj + 5 t t k, t. (a) Show that the curve lies on a sphere centered at the origin. (b) Where does the
Exam 2 Summary. 1. The domain of a function is the set of all possible inputes of the function and the range is the set of all outputs.
 Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Exam 2 Summary Disclaimer: The exam 2 covers lectures 9-15, inclusive. This is mostly about limits, continuity and differentiation of functions of 2 and 3 variables, and some applications. The complete
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III October 26, 2012 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Vocabulary Check. Section 10.8 Graphs of Polar Equations not collinear The points are collinear.
 Section.8 Grphs of Polr Equtions 98 9. Points:,,,,.,... The points re colliner. 9. Points:.,,.,,.,... not colliner. Section.8 Grphs of Polr Equtions When grphing polr equtions:. Test for symmetry. () )
Section.8 Grphs of Polr Equtions 98 9. Points:,,,,.,... The points re colliner. 9. Points:.,,.,,.,... not colliner. Section.8 Grphs of Polr Equtions When grphing polr equtions:. Test for symmetry. () )
Polar coordinates 5C. 1 a. a 4. π = 0 (0) is a circle centre, 0. and radius. The area of the semicircle is π =. π a
 Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
Polr coordintes 5C r cos Are cos d (cos + ) sin + () + 8 cos cos r cos is circle centre, nd rdius. The re of the semicircle is. 8 Person Eduction Ltd 8. Copying permitted for purchsing institution only.
Multivariable integration. Multivariable integration. Iterated integration
 Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Multivrible integrtion Multivrible integrtion Integrtion is ment to nswer the question how muh, depending on the problem nd how we set up the integrl we n be finding how muh volume, how muh surfe re, how
Name: ID: Section: Math 233 Exam 2. Page 1. This exam has 17 questions:
 Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
Page Name: ID: Section: This exam has 7 questions: 5 multiple choice questions worth 5 points each. 2 hand graded questions worth 25 points total. Important: No graphing calculators! Any non scientific
MATH 105: Midterm #1 Practice Problems
 Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
Name: MATH 105: Midterm #1 Practice Problems 1. TRUE or FALSE, plus explanation. Give a full-word answer TRUE or FALSE. If the statement is true, explain why, using concepts and results from class to justify
MATH Exam 2 Solutions November 16, 2015
 MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
MATH 1.54 Exam Solutions November 16, 15 1. Suppose f(x, y) is a differentiable function such that it and its derivatives take on the following values: (x, y) f(x, y) f x (x, y) f y (x, y) f xx (x, y)
i + u 2 j be the unit vector that has its initial point at (a, b) and points in the desired direction. It determines a line in the xy-plane:
 1 Directional Derivatives and Gradients Suppose we need to compute the rate of change of f(x, y) with respect to the distance from a point (a, b) in some direction. Let u = u 1 i + u 2 j be the unit vector
1 Directional Derivatives and Gradients Suppose we need to compute the rate of change of f(x, y) with respect to the distance from a point (a, b) in some direction. Let u = u 1 i + u 2 j be the unit vector
The Chain Rule, Higher Partial Derivatives & Opti- mization
 The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
The Chain Rule, Higher Partial Derivatives & Opti- Unit #21 : mization Goals: We will study the chain rule for functions of several variables. We will compute and study the meaning of higher partial derivatives.
Practice problems from old exams for math 233
 Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Practice problems from old exams for math 233 William H. Meeks III January 14, 2010 Disclaimer: Your instructor covers far more materials that we can possibly fit into a four/five questions exams. These
Math 148 Exam III Practice Problems
 Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
Math 48 Exam III Practice Problems This review should not be used as your sole source for preparation for the exam. You should also re-work all examples given in lecture, all homework problems, all lab
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES
 MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
MAXIMUM FLOWS IN FUZZY NETWORKS WITH FUNNEL-SHAPED NODES Romn V. Tyshchuk Informtion Systems Deprtment, AMI corportion, Donetsk, Ukrine E-mil: rt_science@hotmil.com 1 INTRODUCTION During the considertion
FP2 POLAR COORDINATES: PAST QUESTIONS
 FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
FP POLAR COORDINATES: PAST QUESTIONS. The curve C hs polr eqution r = cosθ, () Sketch the curve C. () (b) Find the polr coordintes of the points where tngents to C re prllel to the initil line. (6) (c)
Section 10.2 Graphing Polar Equations
 Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
Section 10.2 Grphing Polr Equtions OBJECTIVE 1: Sketching Equtions of the Form rcos, rsin, r cos r sin c nd Grphs of Polr Equtions of the Form rcos, rsin, r cos r sin c, nd where,, nd c re constnts. The
4 to find the dimensions of the rectangle that have the maximum area. 2y A =?? f(x, y) = (2x)(2y) = 4xy
 Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
Optimization Constrained optimization and Lagrange multipliers Constrained optimization is what it sounds like - the problem of finding a maximum or minimum value (optimization), subject to some other
c The scaffold pole EL is 8 m long. How far does it extend beyond the line JK?
 3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
3 7. 7.2 Trigonometry in three dimensions Questions re trgeted t the grdes indicted The digrm shows the ck of truck used to crry scffold poles. L K G m J F C 0.8 m H E 3 m D 6.5 m Use Pythgors Theorem
NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES
 At Mth Univ Comenine Vol LXXXV, (06, pp 07 07 NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES G FARID Abstrt In this pper, new Ostrowski-type inequlities in two oordintes re estblished
At Mth Univ Comenine Vol LXXXV, (06, pp 07 07 NEW OSTROWSKI-TYPE INEQUALITIES AND THEIR APPLICATIONS IN TWO COORDINATES G FARID Abstrt In this pper, new Ostrowski-type inequlities in two oordintes re estblished
CS 135: Computer Architecture I. Boolean Algebra. Basic Logic Gates
 Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
Bsic Logic Gtes : Computer Architecture I Boolen Algebr Instructor: Prof. Bhgi Nrhri Dept. of Computer Science Course URL: www.ses.gwu.edu/~bhgiweb/cs35/ Digitl Logic Circuits We sw how we cn build the
MEASURE THE CHARACTERISTIC CURVES RELEVANT TO AN NPN TRANSISTOR
 Electricity Electronics Bipolr Trnsistors MEASURE THE HARATERISTI URVES RELEVANT TO AN NPN TRANSISTOR Mesure the input chrcteristic, i.e. the bse current IB s function of the bse emitter voltge UBE. Mesure
Electricity Electronics Bipolr Trnsistors MEASURE THE HARATERISTI URVES RELEVANT TO AN NPN TRANSISTOR Mesure the input chrcteristic, i.e. the bse current IB s function of the bse emitter voltge UBE. Mesure
Functions of several variables
 Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Chapter 6 Functions of several variables 6.1 Limits and continuity Definition 6.1 (Euclidean distance). Given two points P (x 1, y 1 ) and Q(x, y ) on the plane, we define their distance by the formula
Convolutional Networks. Lecture slides for Chapter 9 of Deep Learning Ian Goodfellow
 Convolutionl Networks Lecture slides for Chpter 9 of Deep Lerning In Goodfellow 2016-09-12 Convolutionl Networks Scle up neurl networks to process very lrge imges / video sequences Sprse connections Prmeter
Convolutionl Networks Lecture slides for Chpter 9 of Deep Lerning In Goodfellow 2016-09-12 Convolutionl Networks Scle up neurl networks to process very lrge imges / video sequences Sprse connections Prmeter
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY
 LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
LECTURE 9: QUADRATIC RESIDUES AND THE LAW OF QUADRATIC RECIPROCITY 1. Bsic roerties of qudrtic residues We now investigte residues with secil roerties of lgebric tye. Definition 1.1. (i) When (, m) 1 nd
Calculus IV Math 2443 Review for Exam 2 on Mon Oct 24, 2016 Exam 2 will cover This is only a sample. Try all the homework problems.
 Calculus IV Math 443 eview for xam on Mon Oct 4, 6 xam will cover 5. 5.. This is only a sample. Try all the homework problems. () o not evaluated the integral. Write as iterated integrals: (x + y )dv,
Calculus IV Math 443 eview for xam on Mon Oct 4, 6 xam will cover 5. 5.. This is only a sample. Try all the homework problems. () o not evaluated the integral. Write as iterated integrals: (x + y )dv,
REVIEW, pages
 REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
REVIEW, pges 510 515 6.1 1. Point P(10, 4) is on the terminl rm of n ngle u in stndrd position. ) Determine the distnce of P from the origin. The distnce of P from the origin is r. r x 2 y 2 Substitute:
For each question, X indicates a correct choice. ANSWER SHEET - BLUE. Question a b c d e Do not write in this column 1 X 2 X 3 X 4 X 5 X 6 X 7 X 8 X
 For each question, X indicates a correct choice. ANSWER SHEET - BLUE X ANSWER SHEET - GREEN X ANSWER SHEET - WHITE X ANSWER SHEET - YELLOW For each question, place an X in the box of your choice. X QUESTION
For each question, X indicates a correct choice. ANSWER SHEET - BLUE X ANSWER SHEET - GREEN X ANSWER SHEET - WHITE X ANSWER SHEET - YELLOW For each question, place an X in the box of your choice. X QUESTION
Math 5BI: Problem Set 1 Linearizing functions of several variables
 Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Math 5BI: Problem Set Linearizing functions of several variables March 9, A. Dot and cross products There are two special operations for vectors in R that are extremely useful, the dot and cross products.
Instructions: Good luck! Math 21a Second Midterm Exam Spring, 2009
 Your Name Your Signature Instructions: Please begin by printing and signing your name in the boxes above and by checking your section in the box to the right You are allowed 2 hours (120 minutes) for this
Your Name Your Signature Instructions: Please begin by printing and signing your name in the boxes above and by checking your section in the box to the right You are allowed 2 hours (120 minutes) for this
Synchronous Machine Parameter Measurement
 Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
Synchronous Mchine Prmeter Mesurement 1 Synchronous Mchine Prmeter Mesurement Introduction Wound field synchronous mchines re mostly used for power genertion but lso re well suited for motor pplictions
MATH 259 FINAL EXAM. Friday, May 8, Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E
 MATH 259 FINAL EXAM 1 Friday, May 8, 2009. NAME: Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E Instructions: 1. Do not separate the pages of the exam.
MATH 259 FINAL EXAM 1 Friday, May 8, 2009. NAME: Alexandra Oleksii Reshma Stephen William Klimova Mostovyi Ramadurai Russel Boney A C D G H B F E Instructions: 1. Do not separate the pages of the exam.
Lecture 15. Global extrema and Lagrange multipliers. Dan Nichols MATH 233, Spring 2018 University of Massachusetts
 Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Lecture 15 Global extrema and Lagrange multipliers Dan Nichols nichols@math.umass.edu MATH 233, Spring 2018 University of Massachusetts March 22, 2018 (2) Global extrema of a multivariable function Definition
Chapter 16. Partial Derivatives
 Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
Chapter 16 Partial Derivatives The use of contour lines to help understand a function whose domain is part of the plane goes back to the year 1774. A group of surveyors had collected a large number of
MATH 8 FALL 2010 CLASS 27, 11/19/ Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits
 MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
MATH 8 FALL 2010 CLASS 27, 11/19/2010 1 Directional derivatives Recall that the definitions of partial derivatives of f(x, y) involved limits lim h 0 f(a + h, b) f(a, b), lim h f(a, b + h) f(a, b) In these
Exercise 1-1. The Sine Wave EXERCISE OBJECTIVE DISCUSSION OUTLINE. Relationship between a rotating phasor and a sine wave DISCUSSION
 Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
Exercise 1-1 The Sine Wve EXERCISE OBJECTIVE When you hve completed this exercise, you will be fmilir with the notion of sine wve nd how it cn be expressed s phsor rotting round the center of circle. You
INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS
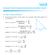 CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
CHAPTER 8 INTRODUCTION TO TRIGONOMETRY AND ITS APPLICATIONS (A) Min Concepts nd Results Trigonometric Rtios of the ngle A in tringle ABC right ngled t B re defined s: sine of A = sin A = side opposite
Lecture 19. Vector fields. Dan Nichols MATH 233, Spring 2018 University of Massachusetts. April 10, 2018.
 Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Lecture 19 Vector fields Dan Nichols nichols@math.umass.edu MATH 233, Spring 218 University of Massachusetts April 1, 218 (2) Chapter 16 Chapter 12: Vectors and 3D geometry Chapter 13: Curves and vector
Section 14.3 Partial Derivatives
 Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
Section 14.3 Partial Derivatives Ruipeng Shen March 20 1 Basic Conceptions If f(x, y) is a function of two variables x and y, suppose we let only x vary while keeping y fixed, say y = b, where b is a constant.
MATH Review Exam II 03/06/11
 MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
MATH 21-259 Review Exam II 03/06/11 1. Find f(t) given that f (t) = sin t i + 3t 2 j and f(0) = i k. 2. Find lim t 0 3(t 2 1) i + cos t j + t t k. 3. Find the points on the curve r(t) at which r(t) and
Ch13 INTRODUCTION TO NUMERICAL TECHNIQUES FOR NONLINEAR SUPERSONIC FLOW
 Ch13 INTRODUCTION TO NUMERICAL TECHNIQUES FOR NONLINEAR SUPERSONIC FLOW Goerning Eqtions for Unste Iniscid Compressible Flow Eler's eqtion Stte eqtions finite-difference nmericl techniqes Goerning Eqtions
Ch13 INTRODUCTION TO NUMERICAL TECHNIQUES FOR NONLINEAR SUPERSONIC FLOW Goerning Eqtions for Unste Iniscid Compressible Flow Eler's eqtion Stte eqtions finite-difference nmericl techniqes Goerning Eqtions
Mathematics 205 HWK 19b Solutions Section 16.2 p750. (x 2 y) dy dx. 2x 2 3
 Mathematics 5 HWK 9b Solutions Section 6. p75 Problem, 6., p75. Evaluate (x y) dy dx. Solution. (x y) dy dx x ( ) y dy dx [ x x dx ] [ ] y x dx Problem 9, 6., p75. For the region as shown, write f da as
Mathematics 5 HWK 9b Solutions Section 6. p75 Problem, 6., p75. Evaluate (x y) dy dx. Solution. (x y) dy dx x ( ) y dy dx [ x x dx ] [ ] y x dx Problem 9, 6., p75. For the region as shown, write f da as
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives
 ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives So far we have dealt with functions of the form y = f(x),
ES 111 Mathematical Methods in the Earth Sciences Lecture Outline 6 - Tues 17th Oct 2017 Functions of Several Variables and Partial Derivatives So far we have dealt with functions of the form y = f(x),
11.7 Maximum and Minimum Values
 Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Arkansas Tech University MATH 2934: Calculus III Dr. Marcel B Finan 11.7 Maximum and Minimum Values Just like functions of a single variable, functions of several variables can have local and global extrema,
Notes on Spherical Triangles
 Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
Notes on Spheril Tringles In order to undertke lultions on the elestil sphere, whether for the purposes of stronomy, nvigtion or designing sundils, some understnding of spheril tringles is essentil. The
ABB STOTZ-KONTAKT. ABB i-bus EIB Current Module SM/S Intelligent Installation Systems. User Manual SM/S In = 16 A AC Un = 230 V AC
 User Mnul ntelligent nstlltion Systems A B 1 2 3 4 5 6 7 8 30 ma 30 ma n = AC Un = 230 V AC 30 ma 9 10 11 12 C ABB STOTZ-KONTAKT Appliction Softwre Current Vlue Threshold/1 Contents Pge 1 Device Chrcteristics...
User Mnul ntelligent nstlltion Systems A B 1 2 3 4 5 6 7 8 30 ma 30 ma n = AC Un = 230 V AC 30 ma 9 10 11 12 C ABB STOTZ-KONTAKT Appliction Softwre Current Vlue Threshold/1 Contents Pge 1 Device Chrcteristics...
DIFFERENTIAL EQUATIONS. A principal model of physical phenomena.
 DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The ordinary differential equation: The initial value: y = f(x, y) y(x 0 )=Y 0 Find a solution Y (x) onsomeintervalx 0 x b. Together these
DIFFERENTIAL EQUATIONS A principal model of physical phenomena. The ordinary differential equation: The initial value: y = f(x, y) y(x 0 )=Y 0 Find a solution Y (x) onsomeintervalx 0 x b. Together these
Math Final Exam - 6/13/2013
 Math - Final Exam - 6/13/13 NAME: SECTION: Directions: For the free response section, you must show all work. Answers without proper justification will not receive full credit. Partial credit will be awarded
Math - Final Exam - 6/13/13 NAME: SECTION: Directions: For the free response section, you must show all work. Answers without proper justification will not receive full credit. Partial credit will be awarded
REVIEW SHEET FOR MIDTERM 2: ADVANCED
 REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
REVIEW SHEET FOR MIDTERM : ADVANCED MATH 195, SECTION 59 (VIPUL NAIK) To maximize efficiency, please bring a copy (print or readable electronic) of this review sheet to the review session. The document
B) 0 C) 1 D) No limit. x2 + y2 4) A) 2 B) 0 C) 1 D) No limit. A) 1 B) 2 C) 0 D) No limit. 8xy 6) A) 1 B) 0 C) π D) -1
 MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
MTH 22 Exam Two - Review Problem Set Name Sketch the surface z = f(x,y). ) f(x, y) = - x2 ) 2) f(x, y) = 2 -x2 - y2 2) Find the indicated limit or state that it does not exist. 4x2 + 8xy + 4y2 ) lim (x,
LECTURE 19 - LAGRANGE MULTIPLIERS
 LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
LECTURE 9 - LAGRANGE MULTIPLIERS CHRIS JOHNSON Abstract. In this lecture we ll describe a way of solving certain optimization problems subject to constraints. This method, known as Lagrange multipliers,
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN. Inventor: Brian L. Baskin
 METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
METHOD OF LOCATION USING SIGNALS OF UNKNOWN ORIGIN Inventor: Brin L. Bskin 1 ABSTRACT The present invention encompsses method of loction comprising: using plurlity of signl trnsceivers to receive one or
Dataflow Language Model. DataFlow Models. Applications of Dataflow. Dataflow Languages. Kahn process networks. A Kahn Process (1)
 The slides contin revisited mterils from: Peter Mrwedel, TU Dortmund Lothr Thiele, ETH Zurich Frnk Vhid, University of liforni, Riverside Dtflow Lnguge Model Drsticlly different wy of looking t computtion:
The slides contin revisited mterils from: Peter Mrwedel, TU Dortmund Lothr Thiele, ETH Zurich Frnk Vhid, University of liforni, Riverside Dtflow Lnguge Model Drsticlly different wy of looking t computtion:
Radiation from Antennas
 Radiation from Antennas Ranga Rodrigo University of Moratuwa November 20, 2008 Ranga Rodrigo (University of Moratuwa) Radiation from Antennas November 20, 2008 1 / 32 Summary of Last Week s Lecture Radiation
Radiation from Antennas Ranga Rodrigo University of Moratuwa November 20, 2008 Ranga Rodrigo (University of Moratuwa) Radiation from Antennas November 20, 2008 1 / 32 Summary of Last Week s Lecture Radiation
Pre-AP Algebra 2 Unit 8 - Lesson 2 Graphing rational functions by plugging in numbers; feature analysis
 Pre-AP Algebra 2 Unit 8 - Lesson 2 Graphing rational functions by plugging in numbers; feature analysis Objectives: Students will be able to: Analyze the features of a rational function: determine domain,
Pre-AP Algebra 2 Unit 8 - Lesson 2 Graphing rational functions by plugging in numbers; feature analysis Objectives: Students will be able to: Analyze the features of a rational function: determine domain,
Estimating Areas. is reminiscent of a Riemann Sum and, amazingly enough, will be called a Riemann Sum. Double Integrals
 Estimating Areas Consider the challenge of estimating the volume of a solid {(x, y, z) 0 z f(x, y), (x, y) }, where is a region in the xy-plane. This may be thought of as the solid under the graph of z
Estimating Areas Consider the challenge of estimating the volume of a solid {(x, y, z) 0 z f(x, y), (x, y) }, where is a region in the xy-plane. This may be thought of as the solid under the graph of z
INTEGRATION OVER NON-RECTANGULAR REGIONS. Contents 1. A slightly more general form of Fubini s Theorem
 INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
INTEGRATION OVER NON-RECTANGULAR REGIONS Contents 1. A slightly more general form of Fubini s Theorem 1 1. A slightly more general form of Fubini s Theorem We now want to learn how to calculate double
Math 232. Calculus III Limits and Continuity. Updated: January 13, 2016 Calculus III Section 14.2
 Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
Math 232 Calculus III Brian Veitch Fall 2015 Northern Illinois University 14.2 Limits and Continuity In this section our goal is to evaluate its of the form f(x, y) = L Let s take a look back at its in
SOLUTIONS 2. PRACTICE EXAM 2. HOURLY. Problem 1) TF questions (20 points) Circle the correct letter. No justifications are needed.
 SOLUIONS 2. PRACICE EXAM 2. HOURLY Math 21a, S03 Problem 1) questions (20 points) Circle the correct letter. No justifications are needed. A function f(x, y) on the plane for which the absolute minimum
SOLUIONS 2. PRACICE EXAM 2. HOURLY Math 21a, S03 Problem 1) questions (20 points) Circle the correct letter. No justifications are needed. A function f(x, y) on the plane for which the absolute minimum
NONCLASSICAL CONSTRUCTIONS II
 NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
NONLSSIL ONSTRUTIONS II hristopher Ohrt UL Mthcircle - Nov. 22, 2015 Now we will try ourselves on oncelet-steiner constructions. You cn only use n (unmrked) stright-edge but you cn ssume tht somewhere
Translate and Classify Conic Sections
 TEKS 9.6 A.5.A, A.5.B, A.5.D, A.5.E Trnslte nd Clssif Conic Sections Before You grphed nd wrote equtions of conic sections. Now You will trnslte conic sections. Wh? So ou cn model motion, s in E. 49. Ke
TEKS 9.6 A.5.A, A.5.B, A.5.D, A.5.E Trnslte nd Clssif Conic Sections Before You grphed nd wrote equtions of conic sections. Now You will trnslte conic sections. Wh? So ou cn model motion, s in E. 49. Ke
Design and Modeling of Substrate Integrated Waveguide based Antenna to Study the Effect of Different Dielectric Materials
 Design nd Modeling of Substrte Integrted Wveguide bsed Antenn to Study the Effect of Different Dielectric Mterils Jgmeet Kour 1, Gurpdm Singh 1, Sndeep Ary 2 1Deprtment of Electronics nd Communiction Engineering,
Design nd Modeling of Substrte Integrted Wveguide bsed Antenn to Study the Effect of Different Dielectric Mterils Jgmeet Kour 1, Gurpdm Singh 1, Sndeep Ary 2 1Deprtment of Electronics nd Communiction Engineering,
Similarly, the point marked in red below is a local minimum for the function, since there are no points nearby that are lower than it:
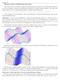 Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Extreme Values of Multivariate Functions Our next task is to develop a method for determining local extremes of multivariate functions, as well as absolute extremes of multivariate functions on closed
Calculus II Fall 2014
 Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
Calculus II Fall 2014 Lecture 3 Partial Derivatives Eitan Angel University of Colorado Monday, December 1, 2014 E. Angel (CU) Calculus II 1 Dec 1 / 13 Introduction Much of the calculus of several variables
