PRE TEST KEY. Math in a Cultural Context*
|
|
|
- Cori Letitia Warner
- 6 years ago
- Views:
Transcription
1 PRE TEST KEY Salmon Fishing: Investigations into A 6 th grade module in the Math in a Cultural Context* UNIVERSITY OF ALASKA FAIRBANKS Student Name: PRE TEST KEY Grade: Teacher: School: Location of School: Date: *This project has been funded by the U.S. Department of Education, Determining the Potential Efficacy of 6th grade Math in a Cultural Context Project, Jerry Lipka, P.I. Total points possible: 46 Total Score: 1
2 1. Draw a line to match the word to its definition. (4 pts. total) WORD DEFINITION Experimental The set of possible outcomes from a single trial of an experiment. Equally Likely One or more outcomes of an experiment. Sample Space Used to predict what might happen after a number of trials. Event All events have the same chance of happening. (4 pts. total) 2. Circle the events that are certain, or have a 100% chance of happening. a. Roll a six-sided die and get either 1,2,3,4,5,6. (circle = 1pt.) b. Weather forecast predicts 100% rain for tomorrow. (do not circle = 1 pt.) c. Flip a coin and get a head or tail. (circle = 1pt.) d. Flip a coin twice and get a head. (do not circle = 1 pt.) 4 pts. total are given if items a and c are the only ones circled and b and d are not circled) 2
3 3. Dora has a coin that is blue on one side and yellow on the other. If she flips the coin twice, what are all the different results she can get? List all possible results below. You can use B for blue and Y for yellow. For finding the sample space: BB, YY, BY, YB (4 pts.) (each of the four outcomes in the sample space is worth 1 pt.) 4. Two coins are each flipped once. Mary wins if the coins match and Sam wins if the coins do not match. Which of the following statements are true or false. Circle your answer. a. Sam is more likely to win. True False b. Mary is more likely to win. True False c. Mary and Sam have the same chances of winning. True False d. Sam can never win. True False (1 pt. each = 4 pts. total) 3
4 5. The chance of snow tomorrow in Fairbanks is 35%. What is the chance that it will not snow tomorrow? Write your answer here: 65 or 65% chance of not snowing. (1 pt.) 6. Peter could not decide whether to walk or catch the bus to school. To decide, he wants to flip a coin 10 times. If more heads come up, then he will walk to school and if more tails come up, he will catch the bus. Peter flipped the coin 10 times, and it landed heads up every time. a. Is this possible? Circle the correct answer. YES NO (1 pt.) b. Write the explanation for your answer in the space below. Each flip can either be a head or a tail side. In this case, it showed a head all 10 times. This may be unlikely, but it is possible. (1 pt.) (2 pts. total) 4
5 7. A six-sided dice is rolled. Find the probability that: a. The number rolled is 2. Write your answer here: 1/6 (1 pt.) b. The number rolled is greater than 4. Write your answer here: 2/6 or 1/3 (1 pt.) c. The number rolled is less than 5. Write your answer here: 4/6 or 2/3 (1 pt.) (3 pts. total) 8. If two dice were rolled over and over again, what sum would you expect to occur most often? a. Write your answer here: 7 (1 pt.) b. How do you know? Write your explanation below: There are more ways (combinations) of getting a 7 than any other sum (1 pt.) (2 pts. total) 5
6 9. There are 4 red marbles, 6 blue marbles, and 5 green marbles in a bag. Find the probability for each of the following events, if only ONE marble is drawn from the bag. a. P(red marble) = 4/15 (1 pt.) b. P(blue marble) = 6/15 or 2/5 (1 pt.) c. P(not green) = 10/15 or 2/3 (1 pt.) d. P(yellow marble) = 0 (1 pt.) (1 pt. each = 4 pts. total) Note: Advanced students may choose to use percentages (%) instead. 6
7 10. For the probability project, two of the students in Grade 6 created games of chance using spinners. Circle the TRUE statement(s): a. You would be more likely to win the game if you used Jack s spinner. (do not circle = 0pt.) b. You would be less likely to win the game if you used Jack s spinner. (do not circle = 0pt.) c. The possibility of winning the game would be the same with either spinner. (circle = 1pt.) d. You would be more likely to win the game if you used Jill s spinner (do not circle = 0pt.) (1 pt. total only given if item c is the only one circled) 7
8 11. Two classes in Grade 6 (6A and 6B) went fishing during the weekend. Class 6A caught 12 king salmon and 12 red salmon. Class 6B caught 8 king salmon, 4 red salmon, and 4 chum salmon. a. Draw a spinner to illustrate the salmon that Class 6A caught. Drawing a spinner with two equal regions (1pt.), One region labeled kings (1pt.) One region labeled reds (1pt.) (3 pts. total) b. Draw a spinner to illustrate the salmon that Class 6B caught. Drawing a spinner that has one region equal to one half of the circle and two other regions each equal to one-fourth of the circle (1pt.) The largest region labeled kings (1pt.) One of the smallest regions labeled reds (1pt.) One of the smallest regions labeled chums (1pt.) (4 pts. total) 8
9 12. Becky s little brother took the labels off of 2 cans of king salmon, 3 cans of red salmon, 1 can of chum salmon, and 4 cans of pink salmon. If Becky chooses one of the cans for lunch, what is the probability that she will choose a can of king salmon? a. Write your answer here: 2/10 or 1/5 (1 pt.) b. Write the explanation for your answer in the space below: Because there are 10 cans total, and 2 of them are king salmon, the fraction would be 2/10, or when reduced 1/5. (1 pt.) (2 pts. total) 13. Suppose you have a brand new, unopened box of 100 chocolate candies. Suppose the label on the box tells you that P(white chocolate candies) = 2/5, and P(dark chocolate candies) = 3/5. a. How many white chocolates are there in your box? Write your answer here: White = 40 (2 pts.) b. How many dark chocolates are there in your box? Write your answer here: Dark = 60 (2 pts.) (4 pts. total) 9
10 14. Students in Mrs. Walker s class made up a game that uses two flat sticks. Each stick is blank on one side and red on the other. This is how the game is played: Each player tosses the two sticks If the sticks both come up blank, the player gets 0 points If the sticks come up one red and one blank, the player gets 1 point If the sticks come up both red, the player gets 1 point The first student to get 10 points wins. a. Is the scoring for this game fair? Circle True or False. True False (1 pt.) False b. Explain your answer: There is not an equal likelihood of getting two reds vs. getting one red and one blank; also it is just as likely to get two blanks as two reds. Or, a student might make a table that shows the sample space (see example below note this is not the only way) to demonstrate that the scoring is not fair. (1 pt.) Stick 1 Stick 2 Red Red, Blank Blank Red Blank Blank Red 10
11 c. If false, show what a fair scoring should be. 1 point blank red or red blank 2 points for blank blank or red red This is because the red/red and blank/blank combinations are each only half as likely as red blank or blank red so should receive twice as many points. (2 pt. total) Note: 1 point each for getting the point value correct for each color combination) 11
PRE TEST. Math in a Cultural Context*
 P grade PRE TEST Salmon Fishing: Investigations into A 6P th module in the Math in a Cultural Context* UNIVERSITY OF ALASKA FAIRBANKS Student Name: Grade: Teacher: School: Location of School: Date: *This
P grade PRE TEST Salmon Fishing: Investigations into A 6P th module in the Math in a Cultural Context* UNIVERSITY OF ALASKA FAIRBANKS Student Name: Grade: Teacher: School: Location of School: Date: *This
What Do You Expect? Concepts
 Important Concepts What Do You Expect? Concepts Examples Probability A number from 0 to 1 that describes the likelihood that an event will occur. Theoretical Probability A probability obtained by analyzing
Important Concepts What Do You Expect? Concepts Examples Probability A number from 0 to 1 that describes the likelihood that an event will occur. Theoretical Probability A probability obtained by analyzing
Statistics and Probability
 Lesson Statistics and Probability Name Use Centimeter Cubes to represent votes from a subgroup of a larger population. In the sample shown, the red cubes are modeled by the dark cubes and represent a yes
Lesson Statistics and Probability Name Use Centimeter Cubes to represent votes from a subgroup of a larger population. In the sample shown, the red cubes are modeled by the dark cubes and represent a yes
b. 2 ; the probability of choosing a white d. P(white) 25, or a a. Since the probability of choosing a
 Applications. a. P(green) =, P(yellow) = 2, or 2, P(red) = 2 ; three of the four blocks are not red. d. 2. a. P(green) = 2 25, P(purple) = 6 25, P(orange) = 2 25, P(yellow) = 5 25, or 5 2 6 2 5 25 25 25
Applications. a. P(green) =, P(yellow) = 2, or 2, P(red) = 2 ; three of the four blocks are not red. d. 2. a. P(green) = 2 25, P(purple) = 6 25, P(orange) = 2 25, P(yellow) = 5 25, or 5 2 6 2 5 25 25 25
Probability. Sometimes we know that an event cannot happen, for example, we cannot fly to the sun. We say the event is impossible
 Probability Sometimes we know that an event cannot happen, for example, we cannot fly to the sun. We say the event is impossible Impossible In summer, it doesn t rain much in Cape Town, so on a chosen
Probability Sometimes we know that an event cannot happen, for example, we cannot fly to the sun. We say the event is impossible Impossible In summer, it doesn t rain much in Cape Town, so on a chosen
2. A bubble-gum machine contains 25 gumballs. There are 12 green, 6 purple, 2 orange, and 5 yellow gumballs.
 A C E Applications Connections Extensions Applications. A bucket contains one green block, one red block, and two yellow blocks. You choose one block from the bucket. a. Find the theoretical probability
A C E Applications Connections Extensions Applications. A bucket contains one green block, one red block, and two yellow blocks. You choose one block from the bucket. a. Find the theoretical probability
Lesson Lesson 3.7 ~ Theoretical Probability
 Theoretical Probability Lesson.7 EXPLORE! sum of two number cubes Step : Copy and complete the chart below. It shows the possible outcomes of one number cube across the top, and a second down the left
Theoretical Probability Lesson.7 EXPLORE! sum of two number cubes Step : Copy and complete the chart below. It shows the possible outcomes of one number cube across the top, and a second down the left
Essential Question How can you list the possible outcomes in the sample space of an experiment?
 . TEXAS ESSENTIAL KNOWLEDGE AND SKILLS G..B Sample Spaces and Probability Essential Question How can you list the possible outcomes in the sample space of an experiment? The sample space of an experiment
. TEXAS ESSENTIAL KNOWLEDGE AND SKILLS G..B Sample Spaces and Probability Essential Question How can you list the possible outcomes in the sample space of an experiment? The sample space of an experiment
Math 1313 Section 6.2 Definition of Probability
 Math 1313 Section 6.2 Definition of Probability Probability is a measure of the likelihood that an event occurs. For example, if there is a 20% chance of rain tomorrow, that means that the probability
Math 1313 Section 6.2 Definition of Probability Probability is a measure of the likelihood that an event occurs. For example, if there is a 20% chance of rain tomorrow, that means that the probability
Key Concepts. Theoretical Probability. Terminology. Lesson 11-1
 Key Concepts Theoretical Probability Lesson - Objective Teach students the terminology used in probability theory, and how to make calculations pertaining to experiments where all outcomes are equally
Key Concepts Theoretical Probability Lesson - Objective Teach students the terminology used in probability theory, and how to make calculations pertaining to experiments where all outcomes are equally
Applications. 28 How Likely Is It? P(green) = 7 P(yellow) = 7 P(red) = 7. P(green) = 7 P(purple) = 7 P(orange) = 7 P(yellow) = 7
 Applications. A bucket contains one green block, one red block, and two yellow blocks. You choose one block from the bucket. a. Find the theoretical probability that you will choose each color. P(green)
Applications. A bucket contains one green block, one red block, and two yellow blocks. You choose one block from the bucket. a. Find the theoretical probability that you will choose each color. P(green)
Grade 8 Math Assignment: Probability
 Grade 8 Math Assignment: Probability Part 1: Rock, Paper, Scissors - The Study of Chance Purpose An introduction of the basic information on probability and statistics Materials: Two sets of hands Paper
Grade 8 Math Assignment: Probability Part 1: Rock, Paper, Scissors - The Study of Chance Purpose An introduction of the basic information on probability and statistics Materials: Two sets of hands Paper
Date. Probability. Chapter
 Date Probability Contests, lotteries, and games offer the chance to win just about anything. You can win a cup of coffee. Even better, you can win cars, houses, vacations, or millions of dollars. Games
Date Probability Contests, lotteries, and games offer the chance to win just about anything. You can win a cup of coffee. Even better, you can win cars, houses, vacations, or millions of dollars. Games
There is no class tomorrow! Have a good weekend! Scores will be posted in Compass early Friday morning J
 STATISTICS 100 EXAM 3 Fall 2016 PRINT NAME (Last name) (First name) *NETID CIRCLE SECTION: L1 12:30pm L2 3:30pm Online MWF 12pm Write answers in appropriate blanks. When no blanks are provided CIRCLE your
STATISTICS 100 EXAM 3 Fall 2016 PRINT NAME (Last name) (First name) *NETID CIRCLE SECTION: L1 12:30pm L2 3:30pm Online MWF 12pm Write answers in appropriate blanks. When no blanks are provided CIRCLE your
Part 1: I can express probability as a fraction, decimal, and percent
 Name: Pattern: Part 1: I can express probability as a fraction, decimal, and percent For #1 to #4, state the probability of each outcome. Write each answer as a) a fraction b) a decimal c) a percent Example:
Name: Pattern: Part 1: I can express probability as a fraction, decimal, and percent For #1 to #4, state the probability of each outcome. Write each answer as a) a fraction b) a decimal c) a percent Example:
Section A Calculating Probabilities & Listing Outcomes Grade F D
 Name: Teacher Assessment Section A Calculating Probabilities & Listing Outcomes Grade F D 1. A fair ordinary six-sided dice is thrown once. The boxes show some of the possible outcomes. Draw a line from
Name: Teacher Assessment Section A Calculating Probabilities & Listing Outcomes Grade F D 1. A fair ordinary six-sided dice is thrown once. The boxes show some of the possible outcomes. Draw a line from
Lesson 3: Chance Experiments with Equally Likely Outcomes
 Lesson : Chance Experiments with Equally Likely Outcomes Classwork Example 1 Jamal, a 7 th grader, wants to design a game that involves tossing paper cups. Jamal tosses a paper cup five times and records
Lesson : Chance Experiments with Equally Likely Outcomes Classwork Example 1 Jamal, a 7 th grader, wants to design a game that involves tossing paper cups. Jamal tosses a paper cup five times and records
Name. Is the game fair or not? Prove your answer with math. If the game is fair, play it 36 times and record the results.
 Homework 5.1C You must complete table. Use math to decide if the game is fair or not. If Period the game is not fair, change the point system to make it fair. Game 1 Circle one: Fair or Not 2 six sided
Homework 5.1C You must complete table. Use math to decide if the game is fair or not. If Period the game is not fair, change the point system to make it fair. Game 1 Circle one: Fair or Not 2 six sided
Lesson 1: Chance Experiments
 Student Outcomes Students understand that a probability is a number between and that represents the likelihood that an event will occur. Students interpret a probability as the proportion of the time that
Student Outcomes Students understand that a probability is a number between and that represents the likelihood that an event will occur. Students interpret a probability as the proportion of the time that
Unit 6: Probability Summative Assessment. 2. The probability of a given event can be represented as a ratio between what two numbers?
 Math 7 Unit 6: Probability Summative Assessment Name Date Knowledge and Understanding 1. Explain the difference between theoretical and experimental probability. 2. The probability of a given event can
Math 7 Unit 6: Probability Summative Assessment Name Date Knowledge and Understanding 1. Explain the difference between theoretical and experimental probability. 2. The probability of a given event can
What is the probability Jordan will pick a red marble out of the bag and land on the red section when spinning the spinner?
 Name: Class: Date: Question #1 Jordan has a bag of marbles and a spinner. The bag of marbles has 10 marbles in it, 6 of which are red. The spinner is divided into 4 equal sections: blue, green, red, and
Name: Class: Date: Question #1 Jordan has a bag of marbles and a spinner. The bag of marbles has 10 marbles in it, 6 of which are red. The spinner is divided into 4 equal sections: blue, green, red, and
SERIES Chance and Probability
 F Teacher Student Book Name Series F Contents Topic Section Chance Answers and (pp. Probability 0) (pp. 0) ordering chance and events probability_ / / relating fractions to likelihood / / chance experiments
F Teacher Student Book Name Series F Contents Topic Section Chance Answers and (pp. Probability 0) (pp. 0) ordering chance and events probability_ / / relating fractions to likelihood / / chance experiments
A 20% B 25% C 50% D 80% 2. Which spinner has a greater likelihood of landing on 5 rather than 3?
 1. At a middle school, 1 of the students have a cell phone. If a student is chosen at 5 random, what is the probability the student does not have a cell phone? A 20% B 25% C 50% D 80% 2. Which spinner
1. At a middle school, 1 of the students have a cell phone. If a student is chosen at 5 random, what is the probability the student does not have a cell phone? A 20% B 25% C 50% D 80% 2. Which spinner
Lesson 4: Calculating Probabilities for Chance Experiments with Equally Likely Outcomes
 Lesson : Calculating Probabilities for Chance Experiments with Equally Likely Outcomes Classwork Example : heoretical Probability In a previous lesson, you saw that to find an estimate of the probability
Lesson : Calculating Probabilities for Chance Experiments with Equally Likely Outcomes Classwork Example : heoretical Probability In a previous lesson, you saw that to find an estimate of the probability
Unit 7 Central Tendency and Probability
 Name: Block: 7.1 Central Tendency 7.2 Introduction to Probability 7.3 Independent Events 7.4 Dependent Events 7.1 Central Tendency A central tendency is a central or value in a data set. We will look at
Name: Block: 7.1 Central Tendency 7.2 Introduction to Probability 7.3 Independent Events 7.4 Dependent Events 7.1 Central Tendency A central tendency is a central or value in a data set. We will look at
3. a. P(white) =, or. b. ; the probability of choosing a white block. d. P(white) =, or. 4. a. = 1 b. 0 c. = 0
 Answers Investigation ACE Assignment Choices Problem. Core, 6 Other Connections, Extensions Problem. Core 6 Other Connections 7 ; unassigned choices from previous problems Problem. Core 7 9 Other Connections
Answers Investigation ACE Assignment Choices Problem. Core, 6 Other Connections, Extensions Problem. Core 6 Other Connections 7 ; unassigned choices from previous problems Problem. Core 7 9 Other Connections
Unit 6: What Do You Expect? Investigation 2: Experimental and Theoretical Probability
 Unit 6: What Do You Expect? Investigation 2: Experimental and Theoretical Probability Lesson Practice Problems Lesson 1: Predicting to Win (Finding Theoretical Probabilities) 1-3 Lesson 2: Choosing Marbles
Unit 6: What Do You Expect? Investigation 2: Experimental and Theoretical Probability Lesson Practice Problems Lesson 1: Predicting to Win (Finding Theoretical Probabilities) 1-3 Lesson 2: Choosing Marbles
Chance and Probability
 F Student Book Name Series F Contents Topic Chance and probability (pp. 0) ordering events relating fractions to likelihood chance experiments fair or unfair the mathletics cup create greedy pig solve
F Student Book Name Series F Contents Topic Chance and probability (pp. 0) ordering events relating fractions to likelihood chance experiments fair or unfair the mathletics cup create greedy pig solve
Ch Probability Outcomes & Trials
 Learning Intentions: Ch. 10.2 Probability Outcomes & Trials Define the basic terms & concepts of probability. Find experimental probabilities. Calculate theoretical probabilities. Vocabulary: Trial: real-world
Learning Intentions: Ch. 10.2 Probability Outcomes & Trials Define the basic terms & concepts of probability. Find experimental probabilities. Calculate theoretical probabilities. Vocabulary: Trial: real-world
Unit 1 Day 1: Sample Spaces and Subsets. Define: Sample Space. Define: Intersection of two sets (A B) Define: Union of two sets (A B)
 Unit 1 Day 1: Sample Spaces and Subsets Students will be able to (SWBAT) describe events as subsets of sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions,
Unit 1 Day 1: Sample Spaces and Subsets Students will be able to (SWBAT) describe events as subsets of sample space (the set of outcomes) using characteristics (or categories) of the outcomes, or as unions,
Math 7 Notes - Unit 7B (Chapter 11) Probability
 Math 7 Notes - Unit 7B (Chapter 11) Probability Probability Syllabus Objective: (7.2)The student will determine the theoretical probability of an event. Syllabus Objective: (7.4)The student will compare
Math 7 Notes - Unit 7B (Chapter 11) Probability Probability Syllabus Objective: (7.2)The student will determine the theoretical probability of an event. Syllabus Objective: (7.4)The student will compare
When a number cube is rolled once, the possible numbers that could show face up are
 C3 Chapter 12 Understanding Probability Essential question: How can you describe the likelihood of an event? Example 1 Likelihood of an Event When a number cube is rolled once, the possible numbers that
C3 Chapter 12 Understanding Probability Essential question: How can you describe the likelihood of an event? Example 1 Likelihood of an Event When a number cube is rolled once, the possible numbers that
MATH STUDENT BOOK. 6th Grade Unit 7
 MATH STUDENT BOOK 6th Grade Unit 7 Unit 7 Probability and Geometry MATH 607 Probability and Geometry. PROBABILITY 5 INTRODUCTION TO PROBABILITY 6 COMPLEMENTARY EVENTS SAMPLE SPACE 7 PROJECT: THEORETICAL
MATH STUDENT BOOK 6th Grade Unit 7 Unit 7 Probability and Geometry MATH 607 Probability and Geometry. PROBABILITY 5 INTRODUCTION TO PROBABILITY 6 COMPLEMENTARY EVENTS SAMPLE SPACE 7 PROJECT: THEORETICAL
Foundations to Algebra In Class: Investigating Probability
 Foundations to Algebra In Class: Investigating Probability Name Date How can I use probability to make predictions? Have you ever tried to predict which football team will win a big game? If so, you probably
Foundations to Algebra In Class: Investigating Probability Name Date How can I use probability to make predictions? Have you ever tried to predict which football team will win a big game? If so, you probably
MATH STUDENT BOOK. 7th Grade Unit 6
 MATH STUDENT BOOK 7th Grade Unit 6 Unit 6 Probability and Graphing Math 706 Probability and Graphing Introduction 3 1. Probability 5 Theoretical Probability 5 Experimental Probability 13 Sample Space 20
MATH STUDENT BOOK 7th Grade Unit 6 Unit 6 Probability and Graphing Math 706 Probability and Graphing Introduction 3 1. Probability 5 Theoretical Probability 5 Experimental Probability 13 Sample Space 20
A referee flipped a fair coin to decide which football team would start the game with
 Probability Lesson.1 A referee flipped a fair coin to decide which football team would start the game with the ball. The coin was just as likely to land heads as tails. Which way do you think the coin
Probability Lesson.1 A referee flipped a fair coin to decide which football team would start the game with the ball. The coin was just as likely to land heads as tails. Which way do you think the coin
Objectives. Determine whether events are independent or dependent. Find the probability of independent and dependent events.
 Objectives Determine whether events are independent or dependent. Find the probability of independent and dependent events. independent events dependent events conditional probability Vocabulary Events
Objectives Determine whether events are independent or dependent. Find the probability of independent and dependent events. independent events dependent events conditional probability Vocabulary Events
Basic Probability Ideas. Experiment - a situation involving chance or probability that leads to results called outcomes.
 Basic Probability Ideas Experiment - a situation involving chance or probability that leads to results called outcomes. Random Experiment the process of observing the outcome of a chance event Simulation
Basic Probability Ideas Experiment - a situation involving chance or probability that leads to results called outcomes. Random Experiment the process of observing the outcome of a chance event Simulation
Most of the time we deal with theoretical probability. Experimental probability uses actual data that has been collected.
 AFM Unit 7 Day 3 Notes Theoretical vs. Experimental Probability Name Date Definitions: Experiment: process that gives a definite result Outcomes: results Sample space: set of all possible outcomes Event:
AFM Unit 7 Day 3 Notes Theoretical vs. Experimental Probability Name Date Definitions: Experiment: process that gives a definite result Outcomes: results Sample space: set of all possible outcomes Event:
out one marble and then a second marble without replacing the first. What is the probability that both marbles will be white?
 Example: Leah places four white marbles and two black marbles in a bag She plans to draw out one marble and then a second marble without replacing the first What is the probability that both marbles will
Example: Leah places four white marbles and two black marbles in a bag She plans to draw out one marble and then a second marble without replacing the first What is the probability that both marbles will
COMPOUND EVENTS. Judo Math Inc.
 COMPOUND EVENTS Judo Math Inc. 7 th grade Statistics Discipline: Black Belt Training Order of Mastery: Compound Events 1. What are compound events? 2. Using organized Lists (7SP8) 3. Using tables (7SP8)
COMPOUND EVENTS Judo Math Inc. 7 th grade Statistics Discipline: Black Belt Training Order of Mastery: Compound Events 1. What are compound events? 2. Using organized Lists (7SP8) 3. Using tables (7SP8)
Order the fractions from least to greatest. Use Benchmark Fractions to help you. First try to decide which is greater than ½ and which is less than ½
 Outcome G Order the fractions from least to greatest 4 1 7 4 5 3 9 5 8 5 7 10 Use Benchmark Fractions to help you. First try to decide which is greater than ½ and which is less than ½ Likelihood Certain
Outcome G Order the fractions from least to greatest 4 1 7 4 5 3 9 5 8 5 7 10 Use Benchmark Fractions to help you. First try to decide which is greater than ½ and which is less than ½ Likelihood Certain
Use this information to answer the following questions.
 1 Lisa drew a token out of the bag, recorded the result, and then put the token back into the bag. She did this 30 times and recorded the results in a bar graph. Use this information to answer the following
1 Lisa drew a token out of the bag, recorded the result, and then put the token back into the bag. She did this 30 times and recorded the results in a bar graph. Use this information to answer the following
What s the Probability I Can Draw That? Janet Tomlinson & Kelly Edenfield
 What s the Probability I Can Draw That? Janet Tomlinson & Kelly Edenfield Engage Your Brain On your seat you should have found a list of 5 events and a number line on which to rate the probability of those
What s the Probability I Can Draw That? Janet Tomlinson & Kelly Edenfield Engage Your Brain On your seat you should have found a list of 5 events and a number line on which to rate the probability of those
Probability Essential Math 12 Mr. Morin
 Probability Essential Math 12 Mr. Morin Name: Slot: Introduction Probability and Odds Single Event Probability and Odds Two and Multiple Event Experimental and Theoretical Probability Expected Value (Expected
Probability Essential Math 12 Mr. Morin Name: Slot: Introduction Probability and Odds Single Event Probability and Odds Two and Multiple Event Experimental and Theoretical Probability Expected Value (Expected
Lesson 11.3 Independent Events
 Lesson 11.3 Independent Events Draw a tree diagram to represent each situation. 1. Popping a balloon randomly from a centerpiece consisting of 1 black balloon and 1 white balloon, followed by tossing a
Lesson 11.3 Independent Events Draw a tree diagram to represent each situation. 1. Popping a balloon randomly from a centerpiece consisting of 1 black balloon and 1 white balloon, followed by tossing a
Math 7 Notes - Unit 11 Probability
 Math 7 Notes - Unit 11 Probability Probability Syllabus Objective: (7.2)The student will determine the theoretical probability of an event. Syllabus Objective: (7.4)The student will compare theoretical
Math 7 Notes - Unit 11 Probability Probability Syllabus Objective: (7.2)The student will determine the theoretical probability of an event. Syllabus Objective: (7.4)The student will compare theoretical
Lesson 4: Calculating Probabilities for Chance Experiments with Equally Likely Outcomes
 NYS COMMON CORE MAEMAICS CURRICULUM 7 : Calculating Probabilities for Chance Experiments with Equally Likely Classwork Examples: heoretical Probability In a previous lesson, you saw that to find an estimate
NYS COMMON CORE MAEMAICS CURRICULUM 7 : Calculating Probabilities for Chance Experiments with Equally Likely Classwork Examples: heoretical Probability In a previous lesson, you saw that to find an estimate
Lesson 16.1 Assignment
 Lesson 16.1 Assignment Name Date Rolling, Rolling, Rolling... Defining and Representing Probability 1. Rasheed is getting dressed in the dark. He reaches into his sock drawer to get a pair of socks. He
Lesson 16.1 Assignment Name Date Rolling, Rolling, Rolling... Defining and Representing Probability 1. Rasheed is getting dressed in the dark. He reaches into his sock drawer to get a pair of socks. He
Probability Rules. 2) The probability, P, of any event ranges from which of the following?
 Name: WORKSHEET : Date: Answer the following questions. 1) Probability of event E occurring is... P(E) = Number of ways to get E/Total number of outcomes possible in S, the sample space....if. 2) The probability,
Name: WORKSHEET : Date: Answer the following questions. 1) Probability of event E occurring is... P(E) = Number of ways to get E/Total number of outcomes possible in S, the sample space....if. 2) The probability,
This unit will help you work out probability and use experimental probability and frequency trees. Key points
 Get started Probability This unit will help you work out probability and use experimental probability and frequency trees. AO Fluency check There are 0 marbles in a bag. 9 of the marbles are red, 7 are
Get started Probability This unit will help you work out probability and use experimental probability and frequency trees. AO Fluency check There are 0 marbles in a bag. 9 of the marbles are red, 7 are
Grade 6 Math Circles Fall Oct 14/15 Probability
 1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 6 Math Circles Fall 2014 - Oct 14/15 Probability Probability is the likelihood of an event occurring.
1 Faculty of Mathematics Waterloo, Ontario Centre for Education in Mathematics and Computing Grade 6 Math Circles Fall 2014 - Oct 14/15 Probability Probability is the likelihood of an event occurring.
Math 7 /Unit 5 Practice Test: Probability
 Math 7 /Unit 5 Practice Test: Probability Name Date 1. Define probability. 2. Define experimental probability.. Define sample space for an experiment 4. What makes experimental probability different from
Math 7 /Unit 5 Practice Test: Probability Name Date 1. Define probability. 2. Define experimental probability.. Define sample space for an experiment 4. What makes experimental probability different from
Practice 9-1. Probability
 Practice 9-1 Probability You spin a spinner numbered 1 through 10. Each outcome is equally likely. Find the probabilities below as a fraction, decimal, and percent. 1. P(9) 2. P(even) 3. P(number 4. P(multiple
Practice 9-1 Probability You spin a spinner numbered 1 through 10. Each outcome is equally likely. Find the probabilities below as a fraction, decimal, and percent. 1. P(9) 2. P(even) 3. P(number 4. P(multiple
LC OL Probability. ARNMaths.weebly.com. As part of Leaving Certificate Ordinary Level Math you should be able to complete the following.
 A Ryan LC OL Probability ARNMaths.weebly.com Learning Outcomes As part of Leaving Certificate Ordinary Level Math you should be able to complete the following. Counting List outcomes of an experiment Apply
A Ryan LC OL Probability ARNMaths.weebly.com Learning Outcomes As part of Leaving Certificate Ordinary Level Math you should be able to complete the following. Counting List outcomes of an experiment Apply
A. 15 B. 24 C. 45 D. 54
 A spinner is divided into 8 equal sections. Lara spins the spinner 120 times. It lands on purple 30 times. How many more times does Lara need to spin the spinner and have it land on purple for the relative
A spinner is divided into 8 equal sections. Lara spins the spinner 120 times. It lands on purple 30 times. How many more times does Lara need to spin the spinner and have it land on purple for the relative
STATISTICS and PROBABILITY GRADE 6
 Kansas City Area Teachers of Mathematics 2016 KCATM Math Competition STATISTICS and PROBABILITY GRADE 6 INSTRUCTIONS Do not open this booklet until instructed to do so. Time limit: 20 minutes You may use
Kansas City Area Teachers of Mathematics 2016 KCATM Math Competition STATISTICS and PROBABILITY GRADE 6 INSTRUCTIONS Do not open this booklet until instructed to do so. Time limit: 20 minutes You may use
Skills we've learned. Skills we need. 7 3 Independent and Dependent Events. March 17, Alg2 Notes 7.3.notebook
 7 3 Independent and Dependent Events Skills we've learned 1. In a box of 25 switches, 3 are defective. What is the probability of randomly selecting a switch that is not defective? 2. There are 12 E s
7 3 Independent and Dependent Events Skills we've learned 1. In a box of 25 switches, 3 are defective. What is the probability of randomly selecting a switch that is not defective? 2. There are 12 E s
Math. Integrated. Trimester 3 Revision Grade 7. Zayed Al Thani School. ministry of education.
 ministry of education Department of Education and Knowledge Zayed Al Thani School www.z2school.com Integrated Math Grade 7 2017-2018 Trimester 3 Revision الوزارة كتاب عن تغني ال المراجعة هذه 0 Ministry
ministry of education Department of Education and Knowledge Zayed Al Thani School www.z2school.com Integrated Math Grade 7 2017-2018 Trimester 3 Revision الوزارة كتاب عن تغني ال المراجعة هذه 0 Ministry
Probability. Probabilty Impossibe Unlikely Equally Likely Likely Certain
 PROBABILITY Probability The likelihood or chance of an event occurring If an event is IMPOSSIBLE its probability is ZERO If an event is CERTAIN its probability is ONE So all probabilities lie between 0
PROBABILITY Probability The likelihood or chance of an event occurring If an event is IMPOSSIBLE its probability is ZERO If an event is CERTAIN its probability is ONE So all probabilities lie between 0
Mini-Unit. Data & Statistics. Investigation 1: Correlations and Probability in Data
 Mini-Unit Data & Statistics Investigation 1: Correlations and Probability in Data I can Measure Variation in Data and Strength of Association in Two-Variable Data Lesson 3: Probability Probability is a
Mini-Unit Data & Statistics Investigation 1: Correlations and Probability in Data I can Measure Variation in Data and Strength of Association in Two-Variable Data Lesson 3: Probability Probability is a
Worksheets for GCSE Mathematics. Probability. mr-mathematics.com Maths Resources for Teachers. Handling Data
 Worksheets for GCSE Mathematics Probability mr-mathematics.com Maths Resources for Teachers Handling Data Probability Worksheets Contents Differentiated Independent Learning Worksheets Probability Scales
Worksheets for GCSE Mathematics Probability mr-mathematics.com Maths Resources for Teachers Handling Data Probability Worksheets Contents Differentiated Independent Learning Worksheets Probability Scales
a) Getting 10 +/- 2 head in 20 tosses is the same probability as getting +/- heads in 320 tosses
 Question 1 pertains to tossing a fair coin (8 pts.) Fill in the blanks with the correct numbers to make the 2 scenarios equally likely: a) Getting 10 +/- 2 head in 20 tosses is the same probability as
Question 1 pertains to tossing a fair coin (8 pts.) Fill in the blanks with the correct numbers to make the 2 scenarios equally likely: a) Getting 10 +/- 2 head in 20 tosses is the same probability as
This Probability Packet Belongs to:
 This Probability Packet Belongs to: 1 2 Station #1: M & M s 1. What is the sample space of your bag of M&M s? 2. Find the theoretical probability of the M&M s in your bag. Then, place the candy back into
This Probability Packet Belongs to: 1 2 Station #1: M & M s 1. What is the sample space of your bag of M&M s? 2. Find the theoretical probability of the M&M s in your bag. Then, place the candy back into
Probability. facts mental math. problem solving. Power Up F
 LESSON 7 Probability Power Up facts mental math Power Up F a. Estimation: The width of the paperback book is inches. Round this measurement to the nearest inch. in. b. Geometry: An octagon has how many
LESSON 7 Probability Power Up facts mental math Power Up F a. Estimation: The width of the paperback book is inches. Round this measurement to the nearest inch. in. b. Geometry: An octagon has how many
MEP Practice Book ES5. 1. A coin is tossed, and a die is thrown. List all the possible outcomes.
 5 Probability MEP Practice Book ES5 5. Outcome of Two Events 1. A coin is tossed, and a die is thrown. List all the possible outcomes. 2. A die is thrown twice. Copy the diagram below which shows all the
5 Probability MEP Practice Book ES5 5. Outcome of Two Events 1. A coin is tossed, and a die is thrown. List all the possible outcomes. 2. A die is thrown twice. Copy the diagram below which shows all the
MEP Practice Book SA5
 5 Probability 5.1 Probabilities MEP Practice Book SA5 1. Describe the probability of the following events happening, using the terms Certain Very likely Possible Very unlikely Impossible (d) (e) (f) (g)
5 Probability 5.1 Probabilities MEP Practice Book SA5 1. Describe the probability of the following events happening, using the terms Certain Very likely Possible Very unlikely Impossible (d) (e) (f) (g)
PROBABILITY M.K. HOME TUITION. Mathematics Revision Guides. Level: GCSE Foundation Tier
 Mathematics Revision Guides Probability Page 1 of 18 M.K. HOME TUITION Mathematics Revision Guides Level: GCSE Foundation Tier PROBABILITY Version: 2.1 Date: 08-10-2015 Mathematics Revision Guides Probability
Mathematics Revision Guides Probability Page 1 of 18 M.K. HOME TUITION Mathematics Revision Guides Level: GCSE Foundation Tier PROBABILITY Version: 2.1 Date: 08-10-2015 Mathematics Revision Guides Probability
Practice Ace Problems
 Unit 6: Moving Straight Ahead Investigation 2: Experimental and Theoretical Probability Practice Ace Problems Directions: Please complete the necessary problems to earn a maximum of 12 points according
Unit 6: Moving Straight Ahead Investigation 2: Experimental and Theoretical Probability Practice Ace Problems Directions: Please complete the necessary problems to earn a maximum of 12 points according
Benchmark Test : Grade 7 Math. Class/Grade
 Name lass/grade ate enchmark: M.7.P.7. enchmark: M.7.P.7. William tossed a coin four times while waiting for his bus at the bus stop. The first time it landed on heads. The second time it landed on tails.
Name lass/grade ate enchmark: M.7.P.7. enchmark: M.7.P.7. William tossed a coin four times while waiting for his bus at the bus stop. The first time it landed on heads. The second time it landed on tails.
, x {1, 2, k}, where k > 0. (a) Write down P(X = 2). (1) (b) Show that k = 3. (4) Find E(X). (2) (Total 7 marks)
 1. The probability distribution of a discrete random variable X is given by 2 x P(X = x) = 14, x {1, 2, k}, where k > 0. Write down P(X = 2). (1) Show that k = 3. Find E(X). (Total 7 marks) 2. In a game
1. The probability distribution of a discrete random variable X is given by 2 x P(X = x) = 14, x {1, 2, k}, where k > 0. Write down P(X = 2). (1) Show that k = 3. Find E(X). (Total 7 marks) 2. In a game
Revision 6: Similar Triangles and Probability
 Revision 6: Similar Triangles and Probability Name: lass: ate: Mark / 52 % 1) Find the missing length, x, in triangle below 5 cm 6 cm 15 cm 21 cm F 2) Find the missing length, x, in triangle F below 5
Revision 6: Similar Triangles and Probability Name: lass: ate: Mark / 52 % 1) Find the missing length, x, in triangle below 5 cm 6 cm 15 cm 21 cm F 2) Find the missing length, x, in triangle F below 5
Basic Probability. Let! = # 8 # < 13, # N -,., and / are the subsets of! such that - = multiples of four. = factors of 24 / = square numbers
 Basic Probability Let! = # 8 # < 13, # N -,., and / are the subsets of! such that - = multiples of four. = factors of 24 / = square numbers (a) List the elements of!. (b) (i) Draw a Venn diagram to show
Basic Probability Let! = # 8 # < 13, # N -,., and / are the subsets of! such that - = multiples of four. = factors of 24 / = square numbers (a) List the elements of!. (b) (i) Draw a Venn diagram to show
NAME DATE PERIOD. Study Guide and Intervention
 9-1 Section Title The probability of a simple event is a ratio that compares the number of favorable outcomes to the number of possible outcomes. Outcomes occur at random if each outcome occurs by chance.
9-1 Section Title The probability of a simple event is a ratio that compares the number of favorable outcomes to the number of possible outcomes. Outcomes occur at random if each outcome occurs by chance.
Chapter 8: Probability: The Mathematics of Chance
 Chapter 8: Probability: The Mathematics of Chance Free-Response 1. A spinner with regions numbered 1 to 4 is spun and a coin is tossed. Both the number spun and whether the coin lands heads or tails is
Chapter 8: Probability: The Mathematics of Chance Free-Response 1. A spinner with regions numbered 1 to 4 is spun and a coin is tossed. Both the number spun and whether the coin lands heads or tails is
Name Class Date. Introducing Probability Distributions
 Name Class Date Binomial Distributions Extension: Distributions Essential question: What is a probability distribution and how is it displayed? 8-6 CC.9 2.S.MD.5(+) ENGAGE Introducing Distributions Video
Name Class Date Binomial Distributions Extension: Distributions Essential question: What is a probability distribution and how is it displayed? 8-6 CC.9 2.S.MD.5(+) ENGAGE Introducing Distributions Video
1. Theoretical probability is what should happen (based on math), while probability is what actually happens.
 Name: Date: / / QUIZ DAY! Fill-in-the-Blanks: 1. Theoretical probability is what should happen (based on math), while probability is what actually happens. 2. As the number of trials increase, the experimental
Name: Date: / / QUIZ DAY! Fill-in-the-Blanks: 1. Theoretical probability is what should happen (based on math), while probability is what actually happens. 2. As the number of trials increase, the experimental
Compound Events: Making an Organized List
 136 8 7.SP.6 7.SP.8a 7.SP.8b Objective Common Core State Standards Compound Events: Making an Organized List Experience with experiments helps students build on their intuitive sense about probability.
136 8 7.SP.6 7.SP.8a 7.SP.8b Objective Common Core State Standards Compound Events: Making an Organized List Experience with experiments helps students build on their intuitive sense about probability.
Making Predictions with Theoretical Probability
 ? LESSON 6.3 Making Predictions with Theoretical Probability ESSENTIAL QUESTION Proportionality 7.6.H Solve problems using qualitative and quantitative predictions and comparisons from simple experiments.
? LESSON 6.3 Making Predictions with Theoretical Probability ESSENTIAL QUESTION Proportionality 7.6.H Solve problems using qualitative and quantitative predictions and comparisons from simple experiments.
4.2.5 How much can I expect to win?
 4..5 How much can I expect to win? Expected Value Different cultures have developed creative forms of games of chance. For example, native Hawaiians play a game called Konane, which uses markers and a
4..5 How much can I expect to win? Expected Value Different cultures have developed creative forms of games of chance. For example, native Hawaiians play a game called Konane, which uses markers and a
Compound Events. Identify events as simple or compound.
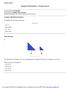
 11.1 Compound Events Lesson Objectives Understand compound events. Represent compound events. Vocabulary compound event possibility diagram simple event tree diagram Understand Compound Events. A compound
11.1 Compound Events Lesson Objectives Understand compound events. Represent compound events. Vocabulary compound event possibility diagram simple event tree diagram Understand Compound Events. A compound
Compound Probability. A to determine the likelihood of two events occurring at the. ***Events can be classified as independent or dependent events.
 Probability 68B A to determine the likelihood of two events occurring at the. ***Events can be classified as independent or dependent events. Independent Events are events in which the result of event
Probability 68B A to determine the likelihood of two events occurring at the. ***Events can be classified as independent or dependent events. Independent Events are events in which the result of event
Page 1 of 22. Website: Mobile:
 Exercise 15.1 Question 1: Complete the following statements: (i) Probability of an event E + Probability of the event not E =. (ii) The probability of an event that cannot happen is. Such as event is called.
Exercise 15.1 Question 1: Complete the following statements: (i) Probability of an event E + Probability of the event not E =. (ii) The probability of an event that cannot happen is. Such as event is called.
STANDARD COMPETENCY : 1. To use the statistics rules, the rules of counting, and the characteristic of probability in problem solving.
 Worksheet 4 th Topic : PROBABILITY TIME : 4 X 45 minutes STANDARD COMPETENCY : 1. To use the statistics rules, the rules of counting, and the characteristic of probability in problem solving. BASIC COMPETENCY:
Worksheet 4 th Topic : PROBABILITY TIME : 4 X 45 minutes STANDARD COMPETENCY : 1. To use the statistics rules, the rules of counting, and the characteristic of probability in problem solving. BASIC COMPETENCY:
Copyright 2015 Edmentum - All rights reserved Picture is not drawn to scale.
 Study Island Copyright 2015 Edmentum - All rights reserved. Generation Date: 05/26/2015 Generated By: Matthew Beyranevand Students Entering Grade 8 Part 2 Questions and Answers Compute with Rational Numbers
Study Island Copyright 2015 Edmentum - All rights reserved. Generation Date: 05/26/2015 Generated By: Matthew Beyranevand Students Entering Grade 8 Part 2 Questions and Answers Compute with Rational Numbers
1. A factory makes calculators. Over a long period, 2 % of them are found to be faulty. A random sample of 100 calculators is tested.
 1. A factory makes calculators. Over a long period, 2 % of them are found to be faulty. A random sample of 0 calculators is tested. Write down the expected number of faulty calculators in the sample. Find
1. A factory makes calculators. Over a long period, 2 % of them are found to be faulty. A random sample of 0 calculators is tested. Write down the expected number of faulty calculators in the sample. Find
Independent Events B R Y
 . Independent Events Lesson Objectives Understand independent events. Use the multiplication rule and the addition rule of probability to solve problems with independent events. Vocabulary independent
. Independent Events Lesson Objectives Understand independent events. Use the multiplication rule and the addition rule of probability to solve problems with independent events. Vocabulary independent
Probability. The MEnTe Program Math Enrichment through Technology. Title V East Los Angeles College
 Probability The MEnTe Program Math Enrichment through Technology Title V East Los Angeles College 2003 East Los Angeles College. All rights reserved. Topics Introduction Empirical Probability Theoretical
Probability The MEnTe Program Math Enrichment through Technology Title V East Los Angeles College 2003 East Los Angeles College. All rights reserved. Topics Introduction Empirical Probability Theoretical
Conditional Probability Worksheet
 Conditional Probability Worksheet EXAMPLE 4. Drug Testing and Conditional Probability Suppose that a company claims it has a test that is 95% effective in determining whether an athlete is using a steroid.
Conditional Probability Worksheet EXAMPLE 4. Drug Testing and Conditional Probability Suppose that a company claims it has a test that is 95% effective in determining whether an athlete is using a steroid.
Making Predictions with Theoretical Probability. ESSENTIAL QUESTION How do you make predictions using theoretical probability?
 L E S S O N 13.3 Making Predictions with Theoretical Probability 7.SP.3.6 predict the approximate relative frequency given the probability. Also 7.SP.3.7a ESSENTIAL QUESTION How do you make predictions
L E S S O N 13.3 Making Predictions with Theoretical Probability 7.SP.3.6 predict the approximate relative frequency given the probability. Also 7.SP.3.7a ESSENTIAL QUESTION How do you make predictions
Review. Natural Numbers: Whole Numbers: Integers: Rational Numbers: Outline Sec Comparing Rational Numbers
 FOUNDATIONS Outline Sec. 3-1 Gallo Name: Date: Review Natural Numbers: Whole Numbers: Integers: Rational Numbers: Comparing Rational Numbers Fractions: A way of representing a division of a whole into
FOUNDATIONS Outline Sec. 3-1 Gallo Name: Date: Review Natural Numbers: Whole Numbers: Integers: Rational Numbers: Comparing Rational Numbers Fractions: A way of representing a division of a whole into
Date Learning Target/s Classwork Homework Self-Assess Your Learning. Pg. 2-3: WDYE 2.3: Designing a Fair Game
 What Do You Expect: Probability and Expected Value Name: Per: Investigation 2: Experimental and Theoretical Probability Date Learning Target/s Classwork Homework Self-Assess Your Learning Mon, Feb. 29
What Do You Expect: Probability and Expected Value Name: Per: Investigation 2: Experimental and Theoretical Probability Date Learning Target/s Classwork Homework Self-Assess Your Learning Mon, Feb. 29
Chance and Probability
 Series Student Chance and Probability My name F Copyright 009 P Learning. All rights reserved. First edition printed 009 in Australia. A catalogue record for this book is available from P Learning Ltd.
Series Student Chance and Probability My name F Copyright 009 P Learning. All rights reserved. First edition printed 009 in Australia. A catalogue record for this book is available from P Learning Ltd.
Probability: Terminology and Examples Spring January 1, / 22
 Probability: Terminology and Examples 18.05 Spring 2014 January 1, 2017 1 / 22 Board Question Deck of 52 cards 13 ranks: 2, 3,..., 9, 10, J, Q, K, A 4 suits:,,,, Poker hands Consists of 5 cards A one-pair
Probability: Terminology and Examples 18.05 Spring 2014 January 1, 2017 1 / 22 Board Question Deck of 52 cards 13 ranks: 2, 3,..., 9, 10, J, Q, K, A 4 suits:,,,, Poker hands Consists of 5 cards A one-pair
Enrichment. Suppose that you are given this information about rolling a number cube.
 ate - Working ackward with Probabilities Suppose that you are given this information about rolling a number cube. P() P() P() an you tell what numbers are marked on the faces of the cube Work backward.
ate - Working ackward with Probabilities Suppose that you are given this information about rolling a number cube. P() P() P() an you tell what numbers are marked on the faces of the cube Work backward.
* How many total outcomes are there if you are rolling two dice? (this is assuming that the dice are different, i.e. 1, 6 isn t the same as a 6, 1)
 Compound probability and predictions Objective: Student will learn counting techniques * Go over HW -Review counting tree -All possible outcomes is called a sample space Go through Problem on P. 12, #2
Compound probability and predictions Objective: Student will learn counting techniques * Go over HW -Review counting tree -All possible outcomes is called a sample space Go through Problem on P. 12, #2
Presentation by Toy Designers: Max Ashley
 A new game for your toy company Presentation by Toy Designers: Shawntee Max Ashley As game designers, we believe that the new game for your company should: Be equally likely, giving each player an equal
A new game for your toy company Presentation by Toy Designers: Shawntee Max Ashley As game designers, we believe that the new game for your company should: Be equally likely, giving each player an equal
Date Learning Target/s Classwork Homework Self-Assess Your Learning. Pg. 2-3: WDYE 3.1: Designing a Spinner. Pg. 5-6: WDYE 3.2: Making Decisions
 What Do You Expect: Probability and Expected Value Name: Per: Investigation 3: Making Decisions and Investigation 4: Area Models Date Learning Target/s Classwork Homework Self-Assess Your Learning Fri,
What Do You Expect: Probability and Expected Value Name: Per: Investigation 3: Making Decisions and Investigation 4: Area Models Date Learning Target/s Classwork Homework Self-Assess Your Learning Fri,
Unit 11 Probability. Round 1 Round 2 Round 3 Round 4
 Study Notes 11.1 Intro to Probability Unit 11 Probability Many events can t be predicted with total certainty. The best thing we can do is say how likely they are to happen, using the idea of probability.
Study Notes 11.1 Intro to Probability Unit 11 Probability Many events can t be predicted with total certainty. The best thing we can do is say how likely they are to happen, using the idea of probability.
Chapter 1: Sets and Probability
 Chapter 1: Sets and Probability Section 1.3-1.5 Recap: Sample Spaces and Events An is an activity that has observable results. An is the result of an experiment. Example 1 Examples of experiments: Flipping
Chapter 1: Sets and Probability Section 1.3-1.5 Recap: Sample Spaces and Events An is an activity that has observable results. An is the result of an experiment. Example 1 Examples of experiments: Flipping
